七年级数学三角形的高,中线与角平分线
文档属性
| 名称 | 七年级数学三角形的高,中线与角平分线 |  | |
| 格式 | zip | ||
| 文件大小 | 668.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-05-14 21:13:48 | ||
图片预览




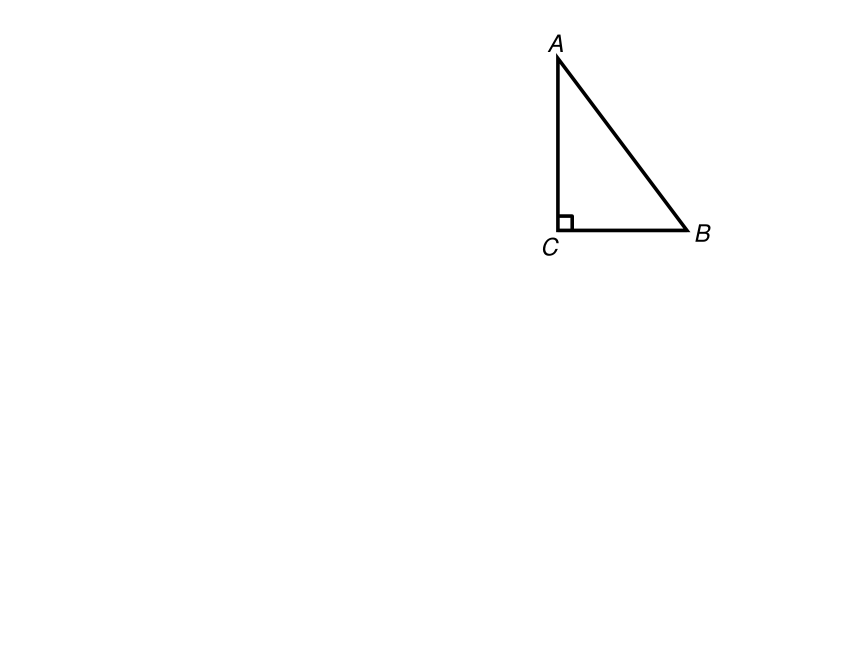


文档简介
(共39张PPT)
7.1.2三角形的高.中线与角平分线
永合中学 孙建清
过直线外一点,画已知直线的垂线,能画几条 怎么画
问题
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5
0 1 2 3 4 5
画法
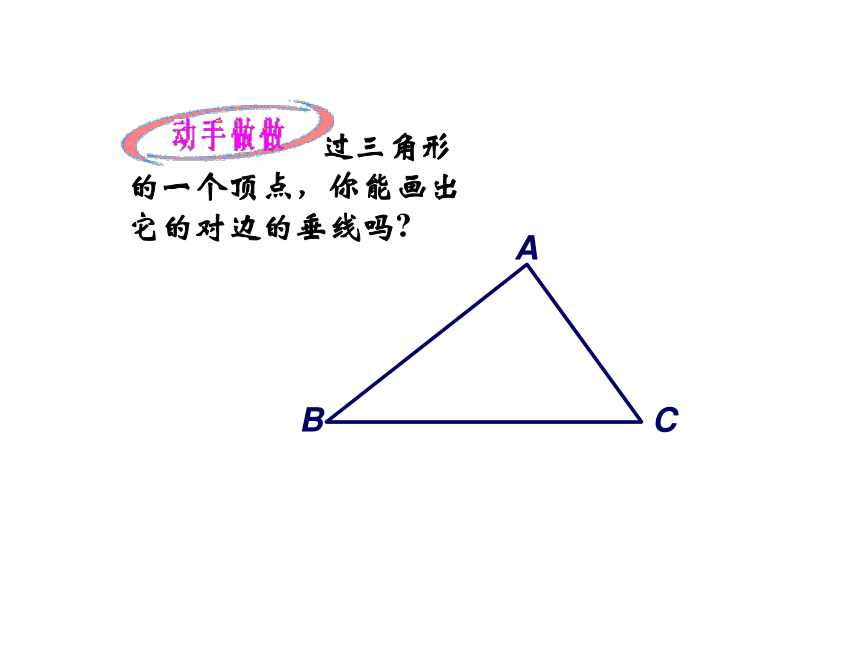
过三角形的一个顶点,你能画出它的对边的垂线吗
B
A
C
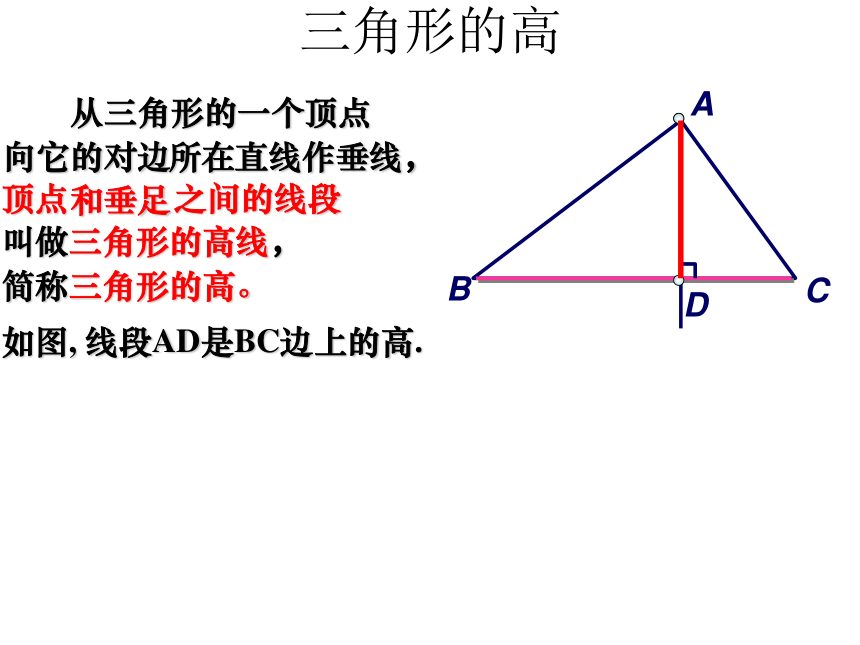
三角形的高
A
从三角形的一个顶点
B
C
向它的对边
所在直线作垂线,
顶点
和垂足
D
之间的线段
叫做三角形的高线,
简称三角形的高。
如图, 线段AD是BC边上的高.
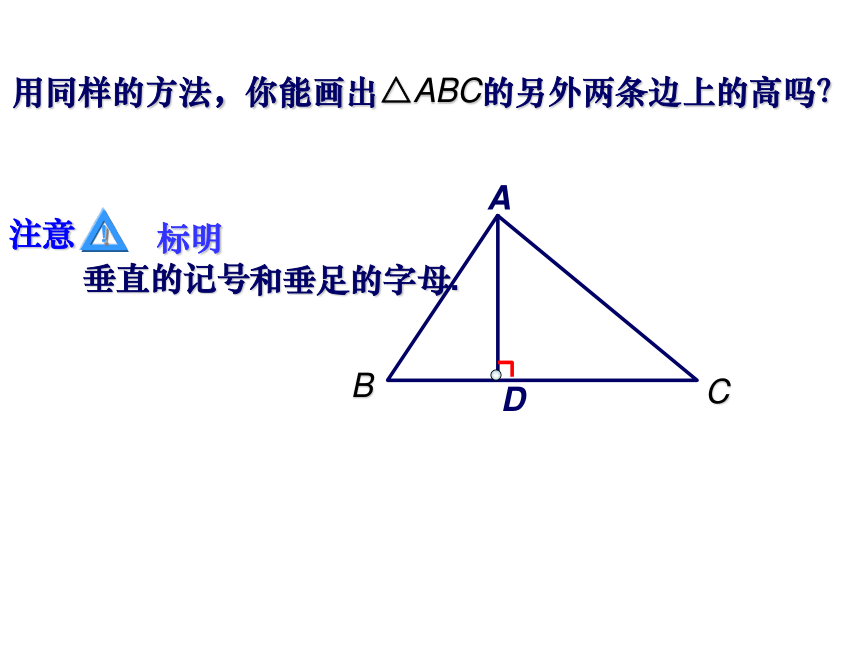
注意
!
标明
垂直的记号
和垂足的字母.
A
B
C
D
用同样的方法,你能画出△ABC的另外两条边上的高吗?
A
B
C
A
B
C
D
E
F
O
A
B
C
A
B
C
D
O
A
B
C
A
B
C
D
E
F
A
B
C
D
O
A
B
C
D
E
F
A
B
C
D
E
F
O
三角形的三条高的特性:
高有几条
高之间是否相交
若相交交点位置
高在三角形内部的数量
钝角三角形
直角三角形
锐角三角形
3
1
1
相交
相交
不相交
3
3
3
三角形内部
直角顶点
------
钝角三角形的三条高
●
钝 角三角形的
三条高不相交于一点
钝角三角形的三条
高所在直线交于一点
练习
如果一个三角形的三条高的交点恰是三角形
的一个顶点,那么这个三角形是( )
A.锐角三角形 B.直角三角形
C.钝角三角形 D.以上答案都对
B
想一想
分别指出图中△ABC 的三条高。
直角边BC边上的
高是 ;
AB
直角边AB边上的
高是 ;
CB
A
B
C
D
E
F
A
B
C
D
斜边AC边上的
高是 ;
BD
AB边上的高是 ;
CE
BC边上的高是 ;
AD
CA边上的高是 ;
BF
三角形的中线
A
C
B
●
●
D
连结ΔABC的顶点A和它所对的边BC的中点D,
线段AD叫做ΔABC的边BC上的中线。
(1)画出ΔABC的另外两边上的中线;
(2)说出哪条线段是ΔABC的哪条边上的中线;
观察ΔABC的三条中线,说说你的发现。
把刚才的锐角三角形换成直角三角形或钝角三角形,结果又怎么样呢?
E
F
●
●
●
●
●
三角形的中线
中线有几条
中线之间是否相交
若相交交点位置
中线在三角形内部的数量
钝角三角形
直角三角形
锐角三角形
3
3
3
3
3
3
相交
相交
相交
三角形内部
三角形内部
三角形内部
三角形的中线
①任何三角形有三条中线,并且
都在三角形 的内部,交与一点。
②三角形的中线是一条线段。
如图在△ABC中,AD是BC 边上的中线
猜想:△ABD的面积和△ADC的面积有什么关系.试说明.
A
B
C
D
E
如右图
∵D是BC的中点
∴BD=DC
而△ABD的面积= BD×AE
△ADC的面积= DC×AE
故△ABD的面积= △ADC的面积
也就是说:三角形的任意一条中线把这个
三角形分成了两个面积相等的三角形。
三角形的角平分线
A
C
B
D
●
●
F
E
●
●
●
●
画∠A的平分线AD,交∠A所对的边BC于点D,
线段AD叫做ΔABC的角平分线。
画出ΔABC的另外两条角平分线;
观察三条角平分线,说说你的发现。
画一画想一想
对于其它的直角、钝角三角形是不是也有同样的结果?
●
三角形的角平分线
有几条
是否相交
若相交交点位置
在三角形内部的数量
钝角三角形
直角三角形
锐角三角形
三角形的角平分线
3
3
3
相交
相交
相交
3
3
3
三角形内部
三角形内部
三角形内部
三角形的角平分线
①任何三角形有三条角平分线,并且都在三角 形的内部,交于一点。
②三角形的角平分线线是一条线段。
1、AD是ΔABC的角平分线(如左图),那么
∠BAC= ∠BAD;
2、AE是ΔABC的中线(如右图),
那么BC= BE。
C
A
D
B
A
B
C
E
2
2
练一练
1、填空:
(1)如图(1),AD,BE,CF是ΔABC的三条中线,则AB=2 ,BD= ,AE= 。
(2)如图(2), AD,BE,CF是ΔABC的三条角平分线,则∠1= , ∠3= , ∠ACB=2 。
AF或BF
DC
AC
∠2
∠ABC
∠4或∠ACF
2.如图,在ΔABC中,AE是中线,AD是角平分线,AF是高。填空:
(1)BE= = ;
(2)∠BAD= = ;
(3)∠AFB= =90°;
(4)SΔABC= 。
CE
BC
∠CAD
∠BAC
∠AFC
BC AF
SΔABE
SΔACE
A
B
C
D
3.如图, AD是ΔABC的边 上的中线,
已知AC=5cm,AB=3cm ,
则ΔADC 与ΔABD的周长差为
2cm
E
D
C
B
A
4、如图AD,AE分别为ΔABC的中线、高,且AB =5cm, A C=8cm,则 ΔACD与 ΔABD 的周长差为 ,ΔABD与ΔADC的面积关系是 .
3cm
相等
A
B
C
D
E
F
O
知识拓展
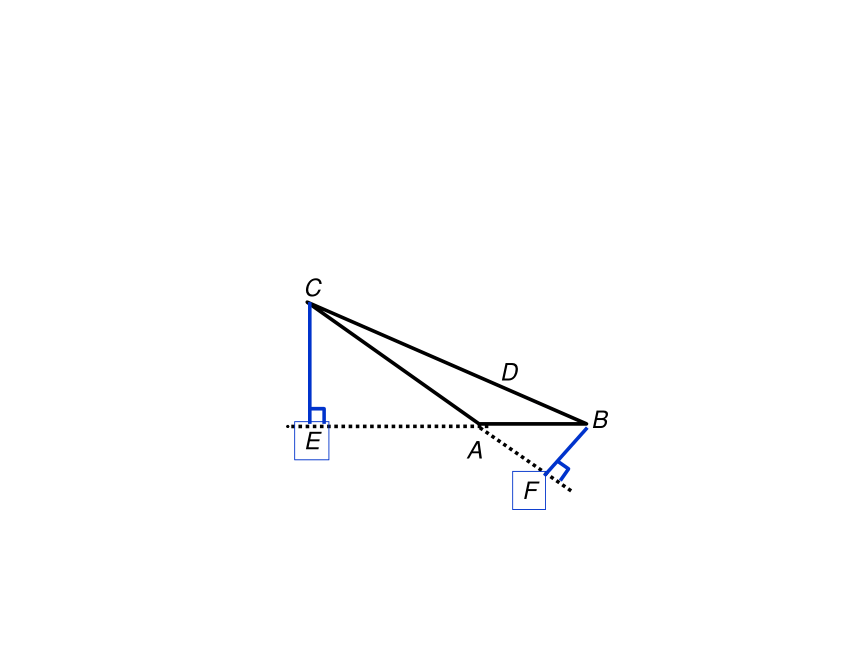
如图 ΔABC 中,高CD,BE,AF相交与点,
则ΔBOC的三条高分别为:
OD ,BF,CE
在ΔABC中,CD是中线,已知BC-AC=5cm, ΔDBC的周长为25cm,求ΔADC的周长.
A
D
B
C
知识拓展
A
B
C
知识应用
D
如图ΔABC是学校的一块菜地,先计划从点D表示的位置(BD:DC=2:1)开始挖一条小水沟,希望小水沟两边的菜地面积相等.你能帮助解决这个问题吗?试试看
E
F
如右图
∵ BD:DC=2:1
∴ △ABD的面积= 2 △ADC的面积
∵ E是AB的中点
∴ △AED的面积= △BED的面积
∵F是AE的中点
∴ △AFD的面积= △ EFD的面积
故△BFD的面积= △ADC的面积+ △AFD的面积
A
B
C
D
E
F
知识应用
如图ΔABC是学校的一块菜地,先计划从点D表示的位置(BD:DC=2:1)开始挖一条小水沟,希望小水沟两边的菜地面积相等.你能帮助解决这个问题吗?试试看
A
B
C
知识应用
D
如图ΔABC是学校的一块菜地,先计划从点D表示的位置(BD:DC=2:1)开始挖一条小水沟,希望小水沟两边的菜地面积相等.你能帮助解决这个问题吗?试试看
E
F
如右图
∵ BD:DC=2:1
∴ △ABD的面积= 2 △ADC的面积
∵ E是AB的中点
∴ △AED的面积= △BED的面积
∵F是AE的中点
∴ △AFD的面积= △ EFA的面积
故△BFD的面积= △ADC的面积+ △AFD的面积
A
B
C
知识应用
D
E
F
如图ΔABC是学校的一块菜地,先计划从点D表示的位置(BD:DC=2:1)开始挖一条小水沟,希望小水沟两边的菜地面积相等.你能帮助解决这个问题吗?试试看
通过本节课的学习,你有哪些收获?
小结
王国维在《人间词话》说:“古今之成大事业、大学问者,必经过三种之境界:
‘昨夜西风凋碧树。独上高楼,望尽天涯路’。
衣带渐宽终不悔,为伊消得人憔悴。’
众里寻他千百度,蓦然回首,那人却在,灯火阑珊处’。
直角三角形的三条高
做一做
A
B
C
直角边BC边上的高是 ;
AB
直角边AB边上的高是 ;
CB
D
斜边AC边上的高是 ;
BD
锐角三角形的三条高
每人准备一个锐角三角形纸片。
(1) 你能画出这个三角形的三条高吗
做一做
(3) 这三条高之间有怎样的位置关系?
将你的结果与同伴进行交流.
锐角三角形的三条高交于同一点.
(2) 你能用折纸的办法得到它们吗
O
锐角三角形的三条高是
在三角形的内部还是外部
使折痕过顶点,顶点的对边边缘重合
锐角三角形的三条高
都在三角形的内部。
拓展练习
拓展练习
2、 如果一个三角形的三条高的交点恰是三角形的一个顶点,那么这个三角形是( )
A.锐角三角形 B.直角三角形
C.钝角三角形 D.锐角三角形
3、三角形的三条高相交于一点,此一点定在( )
A. 三角形的内部 B.三角形的外部
C.三角形的一条边上 D. 不能确定
1、下列各组图形中,哪一组图形中AD是△ABC 的高( )
A
D
C
B
A
B
C
D
A
B
C
D
A
B
C
D
(A)
(B)
(C)
(D)
7.1.2三角形的高.中线与角平分线
永合中学 孙建清
过直线外一点,画已知直线的垂线,能画几条 怎么画
问题
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5
0 1 2 3 4 5
画法
过三角形的一个顶点,你能画出它的对边的垂线吗
B
A
C
三角形的高
A
从三角形的一个顶点
B
C
向它的对边
所在直线作垂线,
顶点
和垂足
D
之间的线段
叫做三角形的高线,
简称三角形的高。
如图, 线段AD是BC边上的高.
注意
!
标明
垂直的记号
和垂足的字母.
A
B
C
D
用同样的方法,你能画出△ABC的另外两条边上的高吗?
A
B
C
A
B
C
D
E
F
O
A
B
C
A
B
C
D
O
A
B
C
A
B
C
D
E
F
A
B
C
D
O
A
B
C
D
E
F
A
B
C
D
E
F
O
三角形的三条高的特性:
高有几条
高之间是否相交
若相交交点位置
高在三角形内部的数量
钝角三角形
直角三角形
锐角三角形
3
1
1
相交
相交
不相交
3
3
3
三角形内部
直角顶点
------
钝角三角形的三条高
●
钝 角三角形的
三条高不相交于一点
钝角三角形的三条
高所在直线交于一点
练习
如果一个三角形的三条高的交点恰是三角形
的一个顶点,那么这个三角形是( )
A.锐角三角形 B.直角三角形
C.钝角三角形 D.以上答案都对
B
想一想
分别指出图中△ABC 的三条高。
直角边BC边上的
高是 ;
AB
直角边AB边上的
高是 ;
CB
A
B
C
D
E
F
A
B
C
D
斜边AC边上的
高是 ;
BD
AB边上的高是 ;
CE
BC边上的高是 ;
AD
CA边上的高是 ;
BF
三角形的中线
A
C
B
●
●
D
连结ΔABC的顶点A和它所对的边BC的中点D,
线段AD叫做ΔABC的边BC上的中线。
(1)画出ΔABC的另外两边上的中线;
(2)说出哪条线段是ΔABC的哪条边上的中线;
观察ΔABC的三条中线,说说你的发现。
把刚才的锐角三角形换成直角三角形或钝角三角形,结果又怎么样呢?
E
F
●
●
●
●
●
三角形的中线
中线有几条
中线之间是否相交
若相交交点位置
中线在三角形内部的数量
钝角三角形
直角三角形
锐角三角形
3
3
3
3
3
3
相交
相交
相交
三角形内部
三角形内部
三角形内部
三角形的中线
①任何三角形有三条中线,并且
都在三角形 的内部,交与一点。
②三角形的中线是一条线段。
如图在△ABC中,AD是BC 边上的中线
猜想:△ABD的面积和△ADC的面积有什么关系.试说明.
A
B
C
D
E
如右图
∵D是BC的中点
∴BD=DC
而△ABD的面积= BD×AE
△ADC的面积= DC×AE
故△ABD的面积= △ADC的面积
也就是说:三角形的任意一条中线把这个
三角形分成了两个面积相等的三角形。
三角形的角平分线
A
C
B
D
●
●
F
E
●
●
●
●
画∠A的平分线AD,交∠A所对的边BC于点D,
线段AD叫做ΔABC的角平分线。
画出ΔABC的另外两条角平分线;
观察三条角平分线,说说你的发现。
画一画想一想
对于其它的直角、钝角三角形是不是也有同样的结果?
●
三角形的角平分线
有几条
是否相交
若相交交点位置
在三角形内部的数量
钝角三角形
直角三角形
锐角三角形
三角形的角平分线
3
3
3
相交
相交
相交
3
3
3
三角形内部
三角形内部
三角形内部
三角形的角平分线
①任何三角形有三条角平分线,并且都在三角 形的内部,交于一点。
②三角形的角平分线线是一条线段。
1、AD是ΔABC的角平分线(如左图),那么
∠BAC= ∠BAD;
2、AE是ΔABC的中线(如右图),
那么BC= BE。
C
A
D
B
A
B
C
E
2
2
练一练
1、填空:
(1)如图(1),AD,BE,CF是ΔABC的三条中线,则AB=2 ,BD= ,AE= 。
(2)如图(2), AD,BE,CF是ΔABC的三条角平分线,则∠1= , ∠3= , ∠ACB=2 。
AF或BF
DC
AC
∠2
∠ABC
∠4或∠ACF
2.如图,在ΔABC中,AE是中线,AD是角平分线,AF是高。填空:
(1)BE= = ;
(2)∠BAD= = ;
(3)∠AFB= =90°;
(4)SΔABC= 。
CE
BC
∠CAD
∠BAC
∠AFC
BC AF
SΔABE
SΔACE
A
B
C
D
3.如图, AD是ΔABC的边 上的中线,
已知AC=5cm,AB=3cm ,
则ΔADC 与ΔABD的周长差为
2cm
E
D
C
B
A
4、如图AD,AE分别为ΔABC的中线、高,且AB =5cm, A C=8cm,则 ΔACD与 ΔABD 的周长差为 ,ΔABD与ΔADC的面积关系是 .
3cm
相等
A
B
C
D
E
F
O
知识拓展
如图 ΔABC 中,高CD,BE,AF相交与点,
则ΔBOC的三条高分别为:
OD ,BF,CE
在ΔABC中,CD是中线,已知BC-AC=5cm, ΔDBC的周长为25cm,求ΔADC的周长.
A
D
B
C
知识拓展
A
B
C
知识应用
D
如图ΔABC是学校的一块菜地,先计划从点D表示的位置(BD:DC=2:1)开始挖一条小水沟,希望小水沟两边的菜地面积相等.你能帮助解决这个问题吗?试试看
E
F
如右图
∵ BD:DC=2:1
∴ △ABD的面积= 2 △ADC的面积
∵ E是AB的中点
∴ △AED的面积= △BED的面积
∵F是AE的中点
∴ △AFD的面积= △ EFD的面积
故△BFD的面积= △ADC的面积+ △AFD的面积
A
B
C
D
E
F
知识应用
如图ΔABC是学校的一块菜地,先计划从点D表示的位置(BD:DC=2:1)开始挖一条小水沟,希望小水沟两边的菜地面积相等.你能帮助解决这个问题吗?试试看
A
B
C
知识应用
D
如图ΔABC是学校的一块菜地,先计划从点D表示的位置(BD:DC=2:1)开始挖一条小水沟,希望小水沟两边的菜地面积相等.你能帮助解决这个问题吗?试试看
E
F
如右图
∵ BD:DC=2:1
∴ △ABD的面积= 2 △ADC的面积
∵ E是AB的中点
∴ △AED的面积= △BED的面积
∵F是AE的中点
∴ △AFD的面积= △ EFA的面积
故△BFD的面积= △ADC的面积+ △AFD的面积
A
B
C
知识应用
D
E
F
如图ΔABC是学校的一块菜地,先计划从点D表示的位置(BD:DC=2:1)开始挖一条小水沟,希望小水沟两边的菜地面积相等.你能帮助解决这个问题吗?试试看
通过本节课的学习,你有哪些收获?
小结
王国维在《人间词话》说:“古今之成大事业、大学问者,必经过三种之境界:
‘昨夜西风凋碧树。独上高楼,望尽天涯路’。
衣带渐宽终不悔,为伊消得人憔悴。’
众里寻他千百度,蓦然回首,那人却在,灯火阑珊处’。
直角三角形的三条高
做一做
A
B
C
直角边BC边上的高是 ;
AB
直角边AB边上的高是 ;
CB
D
斜边AC边上的高是 ;
BD
锐角三角形的三条高
每人准备一个锐角三角形纸片。
(1) 你能画出这个三角形的三条高吗
做一做
(3) 这三条高之间有怎样的位置关系?
将你的结果与同伴进行交流.
锐角三角形的三条高交于同一点.
(2) 你能用折纸的办法得到它们吗
O
锐角三角形的三条高是
在三角形的内部还是外部
使折痕过顶点,顶点的对边边缘重合
锐角三角形的三条高
都在三角形的内部。
拓展练习
拓展练习
2、 如果一个三角形的三条高的交点恰是三角形的一个顶点,那么这个三角形是( )
A.锐角三角形 B.直角三角形
C.钝角三角形 D.锐角三角形
3、三角形的三条高相交于一点,此一点定在( )
A. 三角形的内部 B.三角形的外部
C.三角形的一条边上 D. 不能确定
1、下列各组图形中,哪一组图形中AD是△ABC 的高( )
A
D
C
B
A
B
C
D
A
B
C
D
A
B
C
D
(A)
(B)
(C)
(D)
