人教版八上高分笔记之导与练 11.1.2 与三角形有关的线段(原卷+答案)
文档属性
| 名称 | 人教版八上高分笔记之导与练 11.1.2 与三角形有关的线段(原卷+答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-04 19:48:05 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
三角形
11.1与三角形有关的线段
三角形的高、中线、角平分线、三角形的稳定性
知识点:
如图,AD,AE,AF分别是ΔABC的高,中线和角平分线。填空:
(1)∠ADB=
=90°
(2)BE=
=BC
(3)∠BAF=
=∠BAC
易错点:
如图,在ΔABC中。
(1)画出BC边上的高;
(2)画出AC边上的中线;
(3)画出经过点C的ΔABC的角平分线。
〖点睛〗①注意三角形的高、中线、角平分线都是线段;
②钝角三角形有两条高在三角形的外部。
典型例题:
题型一
与高有关的计算或证明
如图,AB⊥BD,垂足为B,AC⊥CD,垂足为C,且AC与BD相交于点E.若AE=5.DE=2,CD=,求AB的长。
变式练习
如图,已知AD⊥BC,BF⊥CF,且AD=2,BC=8,BF=4,那么AC的长度为(
)
A.2
B.3
C.4
D.5
在ΔABC中,∠ABC=90°,AB=3,BC=4,AC=5,则ΔABC的三条高之和为
例2、如图,在ΔABC中,AB=AC,点D在BC上(D不是BC的中点),
DE⊥AB于点E,DF⊥AC于点?F,BG⊥AC于点G.求证:BG=DE+DF.?
变式练习:
如图,BE,CF均是ΔABC的中线,且BE=CF,AM⊥CF于点M,AN⊥BE于点N?
求证:AM=AN.
题型二
与三角形中线有关的计算
例3、在ΔABC中,AB=AC,BD为ΔABC的中线,且BD将ΔABC的周长分为12cm
与15cm两部分,求ΔABC各边的长.
变式练习:
如图,在ΔABC中,AB>BC,AB=2AC,边AC上的中线BD把ΔABC的周长分成30和20两部分,求AB和BC的长.
?
例4、如图,在ΔABC中,已知D,E,F分别为BC,AD,EC的中点,且S△ABC=12,
则图中阴影部分的面积为(
)
A.1
B.2???????C.3
D.4
变式练习:
如图,在ΔABC中,D,E,F分别是AC,BD,AE的中点.若ΔDEF
的面积为1,则ΔABC的面积是(????)
A.3
B.4
C.8
D.12
2.如图,ΔABC三边上的中线AD,BE,CF交于点G.若S△ABC=24,则图中阴影部分的面积是__
基础练习
1.如图,AD⊥BE,垂足为D,点C在BE上,以AD为高的三角形有(
)
A.6个
B.5个
C.4个
D.3个
1题
2题图
3题
2.如图,在ΔABC中,BC边上的高是AB,在ΔAEC中,AE边上的高是
3.如图,已知AD为ΔABC的中线,AB=12cm,AC=9cm,ΔACD的周长为27cm,则
ΔABD的周长为
cm.
4.已知AD是ΔABC的高,∠BAD=60°,∠CAD=20°,则∠BAC的度数为
第5题
如图,D,E分别是ΔABC的边AB,BC上的点,AD=2BD,BE=CE.设ΔADF的面积
为S1,ΔCEF的面积为S2,若SΔABC=6,则S1-S2的值为
.
6.【教材变式】(P9第8题改)如图,在ΔABC中,AE,CD是ΔABC的两条高,AB=4,CD=2.
(1)请画出AE,CD;
(2)求ΔABC的面积;
(3)若AE=3,求BC的长.
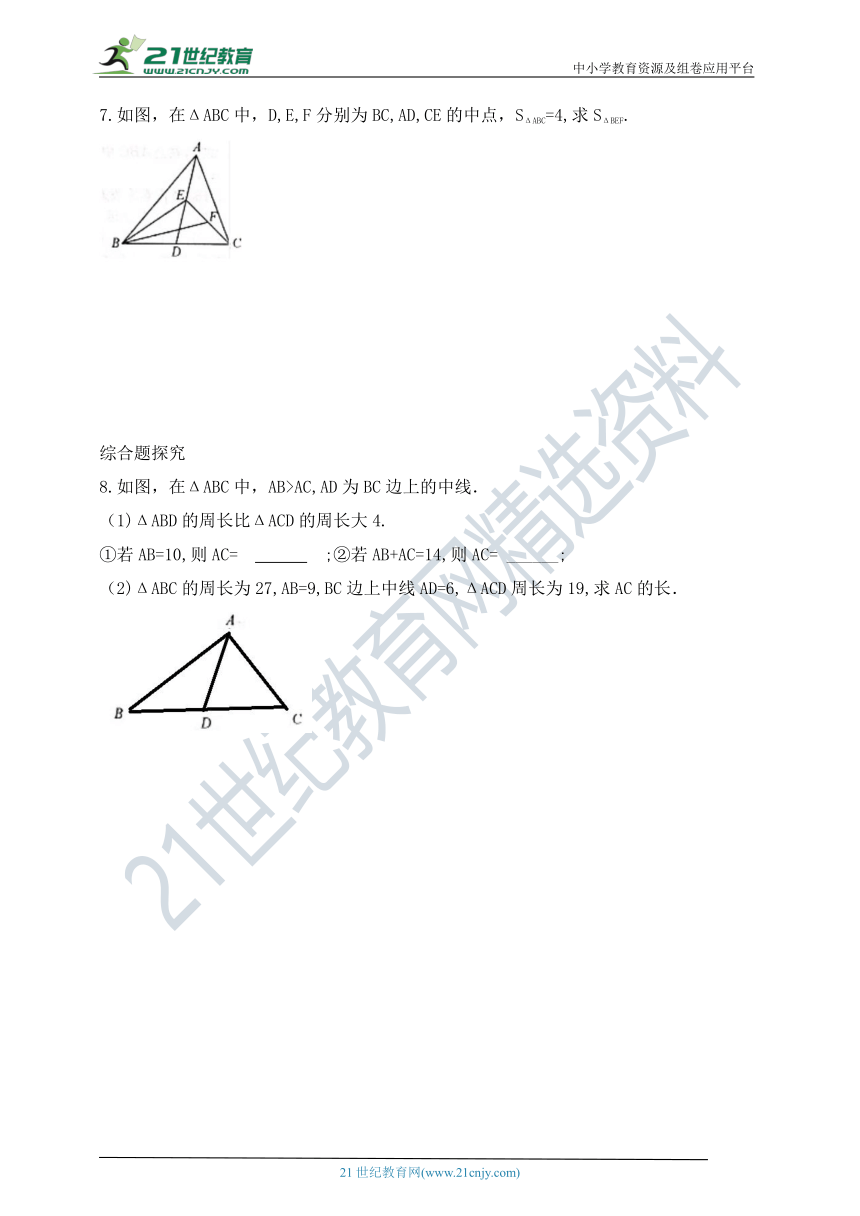
7.如图,在ΔABC中,D,E,F分别为BC,AD,CE的中点,SΔABC=4,求SΔBEF.
综合题探究
8.如图,在ΔABC中,AB>AC,AD为BC边上的中线.
(1)ΔABD的周长比ΔACD的周长大4.
①若AB=10,则AC=?
?;②若AB+AC=14,则AC=
______;
(2)ΔABC的周长为27,AB=9,BC边上中线AD=6,ΔACD周长为19,求AC的长.
答案:
知识点:
如图,AD,AE,AF分别是ΔABC的高,中线和角平分线。填空:
(1)∠ADB=∠ADC=90°
(2)BE=CE=BC
(3)∠BAF=∠CAF=∠BAC
易错点:
如图,在ΔABC中。
(1)画出BC边上的高;
(2)画出AC边上的中线;
(3)画出经过点C的ΔABC的角平分线。
〖点睛〗
①注意三角形的高、中线、角平分线都是线段;
②钝角三角形有两条高在三角形的外部。
典型例题:
题型一
与高有关的计算或证明
如图,AB⊥BD,垂足为B,AC⊥CD,垂足为C,且AC与BD相交于点E.若AE=5.DE=2,CD=,求AB的长。
解:在ΔAED中,边DE上的高为AB,边AE上的高为DC,
等面积法
SΔAED=AE·CD=DE·AB
AE=5,DE=2,CD=
x5x=x2·AB.
解得AB=.故AB的长为
变式练习
如图,已知AD⊥BC,BF⊥CF,且AD=2,BC=8,BF=4,那么AC的长度为(
C
)
A.2
B.3
C.4
D.5
在ΔABC中,∠ABC=90°,AB=3,BC=4,AC=5,则ΔABC的三条高之和为9.4
例2、如图,在ΔABC中,AB=AC,点D在BC上(D不是BC的中点),
DE⊥AB于点E,DF⊥AC于点?F,BG⊥AC于点G.求证:BG=DE+DF.?
证明:如图,连接AD..SΔABC=S△ABD+SΔACD,
AC·BG=AB·DE+AC·DF.?
∵AB=AC,.∴.BG=DE+DF.
变式练习:
如图,BE,CF均是ΔABC的中线,且BE=CF,AM⊥CF于点M,AN⊥BE于点N?
求证:AM=AN.
证明:BE,CF均是ΔABC的中线,
AM⊥CF,AN⊥BE,
∴S△ABE=S△ACF=S△ABC
∴AM·CF=AN·BE.
又CF=BE.∴AM=AN.
题型二
与三角形中线有关的计算
例3、在ΔABC中,AB=AC,BD为ΔABC的中线,且BD将ΔABC的周长分为12cm
与15cm两部分,求ΔABC各边的长.
解:设AB=xcm,则AD=CD=AC=xcm.
分两种情况讨论:
(1)如图①,若AB+AD=12cm,则x+x=12.
解得x=8,即AB=AC=8cm,则CD=AD=4cm.
故BC=15-CD=15-4=11(cm).?
:8+8>11,即AB+AC>BC,.能组成三角形.
.此时ΔABC各边的长分别为8cm,8cm,11cm.
如图②,若AB+AD=15cm,则?x+x=15.
解得x=10,即AB=AC=10cm,则CD=AD=5cm.
故BC=12-CD=12-5=7(cm)
∵10+7>10,即AB+BC>AC,∴能组成三角形.
此时ΔABC各边的长分别为10cm,10cm,7cm.
综上所述,ΔABC各边的长分别为8cm,8cm,11cm?或10cm,10cm,7?cm.?
变式练习:
如图,在ΔABC中,AB>BC,AB=2AC,边AC上的中线BD把ΔABC的周长分成30和20两部分,求AB和BC的长.
解:设AC=x,则AB=2x.
BD是中线,
AD=DC=x
∵AB>BC,∴AB+AD>BC+CD,
∴AB+AD=30,BC+CD=20,,2x+x=30.
解得x=12,则AC=12,.AB=2x12=24,
BC=20-x12=14.?
例4、如图,在ΔABC中,已知D,E,F分别为BC,AD,EC的中点,且S△ABC=12,
则图中阴影部分的面积为(
C
)
A.1
B.2???????C.3
D.4
变式练习:
1.如图,在ΔABC中,D,E,F分别是AC,BD,AE的中点.若ΔDEF
的面积为1,则ΔABC的面积是(??C??)
A.3
B.4
C.8
D.12
2.如图,ΔABC三边上的中线AD,BE,CF交于点G.若S△ABC=24,则图中阴影部分的面积是__8
基础练习
1.如图,AD⊥BE,垂足为D,点C在BE上,以AD为高的三角形有(
A
)
A.6个
B.5个
C.4个
D.3个
1题
2题图
3题
2.如图,在ΔABC中,BC边上的高是AB,在ΔAEC中,AE边上的高是CD
3.如图,已知AD为ΔABC的中线,AB=12cm,AC=9cm,ΔACD的周长为27cm,则
ΔABD的周长为
30
cm.
4.已知AD是ΔABC的高,∠BAD=60°,∠CAD=20°,则∠BAC的度数为80°或40°
第5题
6题
7题
5.如图,D,E分别是ΔABC的边AB,BC上的点,AD=2BD,BE=CE.设ΔADF的面积
为S1,ΔCEF的面积为S2,若SΔABC=6,则S1-S2的值为1.
6.【教材变式】(P9第8题改)如图,在ΔABC中,AE,CD是ΔABC的两条高,AB=4,CD=2.
(1)请画出AE,CD;
(2)求ΔABC的面积;
(3)若AE=3,求BC的长.
解:(1)略;(2)4;(3).
7.如图,在ΔABC中,D,E,F分别为BC,AD,CE的中点,SΔABC=4,求SΔBEF.
解:易证SΔABD=SΔADc=2,S△AEC=SΔDEC=SΔBDE=1,SΔBEC=2,.SΔBEF=SΔBCF=1.
综合题探究
8.如图,在ΔABC中,AB>AC,AD为BC边上的中线.
(1)ΔABD的周长比ΔACD的周长大4.
①若AB=10,则AC=?6?;②若AB+AC=14,则AC=5;
(2)ΔABC的周长为27,AB=9,BC边上中线AD=6,ΔACD周长为19,求AC的长.
解:(1)①AC=6;②AB=9,AC=5;
(2)设AC=x,CD=y,:AD是BC边的中线,.BC=2CD=2y,
由题意得x+9+2y=27,x+6+y=19,解得x=8,y=5,..AC=8.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
三角形
11.1与三角形有关的线段
三角形的高、中线、角平分线、三角形的稳定性
知识点:
如图,AD,AE,AF分别是ΔABC的高,中线和角平分线。填空:
(1)∠ADB=
=90°
(2)BE=
=BC
(3)∠BAF=
=∠BAC
易错点:
如图,在ΔABC中。
(1)画出BC边上的高;
(2)画出AC边上的中线;
(3)画出经过点C的ΔABC的角平分线。
〖点睛〗①注意三角形的高、中线、角平分线都是线段;
②钝角三角形有两条高在三角形的外部。
典型例题:
题型一
与高有关的计算或证明
如图,AB⊥BD,垂足为B,AC⊥CD,垂足为C,且AC与BD相交于点E.若AE=5.DE=2,CD=,求AB的长。
变式练习
如图,已知AD⊥BC,BF⊥CF,且AD=2,BC=8,BF=4,那么AC的长度为(
)
A.2
B.3
C.4
D.5
在ΔABC中,∠ABC=90°,AB=3,BC=4,AC=5,则ΔABC的三条高之和为
例2、如图,在ΔABC中,AB=AC,点D在BC上(D不是BC的中点),
DE⊥AB于点E,DF⊥AC于点?F,BG⊥AC于点G.求证:BG=DE+DF.?
变式练习:
如图,BE,CF均是ΔABC的中线,且BE=CF,AM⊥CF于点M,AN⊥BE于点N?
求证:AM=AN.
题型二
与三角形中线有关的计算
例3、在ΔABC中,AB=AC,BD为ΔABC的中线,且BD将ΔABC的周长分为12cm
与15cm两部分,求ΔABC各边的长.
变式练习:
如图,在ΔABC中,AB>BC,AB=2AC,边AC上的中线BD把ΔABC的周长分成30和20两部分,求AB和BC的长.
?
例4、如图,在ΔABC中,已知D,E,F分别为BC,AD,EC的中点,且S△ABC=12,
则图中阴影部分的面积为(
)
A.1
B.2???????C.3
D.4
变式练习:
如图,在ΔABC中,D,E,F分别是AC,BD,AE的中点.若ΔDEF
的面积为1,则ΔABC的面积是(????)
A.3
B.4
C.8
D.12
2.如图,ΔABC三边上的中线AD,BE,CF交于点G.若S△ABC=24,则图中阴影部分的面积是__
基础练习
1.如图,AD⊥BE,垂足为D,点C在BE上,以AD为高的三角形有(
)
A.6个
B.5个
C.4个
D.3个
1题
2题图
3题
2.如图,在ΔABC中,BC边上的高是AB,在ΔAEC中,AE边上的高是
3.如图,已知AD为ΔABC的中线,AB=12cm,AC=9cm,ΔACD的周长为27cm,则
ΔABD的周长为
cm.
4.已知AD是ΔABC的高,∠BAD=60°,∠CAD=20°,则∠BAC的度数为
第5题
如图,D,E分别是ΔABC的边AB,BC上的点,AD=2BD,BE=CE.设ΔADF的面积
为S1,ΔCEF的面积为S2,若SΔABC=6,则S1-S2的值为
.
6.【教材变式】(P9第8题改)如图,在ΔABC中,AE,CD是ΔABC的两条高,AB=4,CD=2.
(1)请画出AE,CD;
(2)求ΔABC的面积;
(3)若AE=3,求BC的长.
7.如图,在ΔABC中,D,E,F分别为BC,AD,CE的中点,SΔABC=4,求SΔBEF.
综合题探究
8.如图,在ΔABC中,AB>AC,AD为BC边上的中线.
(1)ΔABD的周长比ΔACD的周长大4.
①若AB=10,则AC=?
?;②若AB+AC=14,则AC=
______;
(2)ΔABC的周长为27,AB=9,BC边上中线AD=6,ΔACD周长为19,求AC的长.
答案:
知识点:
如图,AD,AE,AF分别是ΔABC的高,中线和角平分线。填空:
(1)∠ADB=∠ADC=90°
(2)BE=CE=BC
(3)∠BAF=∠CAF=∠BAC
易错点:
如图,在ΔABC中。
(1)画出BC边上的高;
(2)画出AC边上的中线;
(3)画出经过点C的ΔABC的角平分线。
〖点睛〗
①注意三角形的高、中线、角平分线都是线段;
②钝角三角形有两条高在三角形的外部。
典型例题:
题型一
与高有关的计算或证明
如图,AB⊥BD,垂足为B,AC⊥CD,垂足为C,且AC与BD相交于点E.若AE=5.DE=2,CD=,求AB的长。
解:在ΔAED中,边DE上的高为AB,边AE上的高为DC,
等面积法
SΔAED=AE·CD=DE·AB
AE=5,DE=2,CD=
x5x=x2·AB.
解得AB=.故AB的长为
变式练习
如图,已知AD⊥BC,BF⊥CF,且AD=2,BC=8,BF=4,那么AC的长度为(
C
)
A.2
B.3
C.4
D.5
在ΔABC中,∠ABC=90°,AB=3,BC=4,AC=5,则ΔABC的三条高之和为9.4
例2、如图,在ΔABC中,AB=AC,点D在BC上(D不是BC的中点),
DE⊥AB于点E,DF⊥AC于点?F,BG⊥AC于点G.求证:BG=DE+DF.?
证明:如图,连接AD..SΔABC=S△ABD+SΔACD,
AC·BG=AB·DE+AC·DF.?
∵AB=AC,.∴.BG=DE+DF.
变式练习:
如图,BE,CF均是ΔABC的中线,且BE=CF,AM⊥CF于点M,AN⊥BE于点N?
求证:AM=AN.
证明:BE,CF均是ΔABC的中线,
AM⊥CF,AN⊥BE,
∴S△ABE=S△ACF=S△ABC
∴AM·CF=AN·BE.
又CF=BE.∴AM=AN.
题型二
与三角形中线有关的计算
例3、在ΔABC中,AB=AC,BD为ΔABC的中线,且BD将ΔABC的周长分为12cm
与15cm两部分,求ΔABC各边的长.
解:设AB=xcm,则AD=CD=AC=xcm.
分两种情况讨论:
(1)如图①,若AB+AD=12cm,则x+x=12.
解得x=8,即AB=AC=8cm,则CD=AD=4cm.
故BC=15-CD=15-4=11(cm).?
:8+8>11,即AB+AC>BC,.能组成三角形.
.此时ΔABC各边的长分别为8cm,8cm,11cm.
如图②,若AB+AD=15cm,则?x+x=15.
解得x=10,即AB=AC=10cm,则CD=AD=5cm.
故BC=12-CD=12-5=7(cm)
∵10+7>10,即AB+BC>AC,∴能组成三角形.
此时ΔABC各边的长分别为10cm,10cm,7cm.
综上所述,ΔABC各边的长分别为8cm,8cm,11cm?或10cm,10cm,7?cm.?
变式练习:
如图,在ΔABC中,AB>BC,AB=2AC,边AC上的中线BD把ΔABC的周长分成30和20两部分,求AB和BC的长.
解:设AC=x,则AB=2x.
BD是中线,
AD=DC=x
∵AB>BC,∴AB+AD>BC+CD,
∴AB+AD=30,BC+CD=20,,2x+x=30.
解得x=12,则AC=12,.AB=2x12=24,
BC=20-x12=14.?
例4、如图,在ΔABC中,已知D,E,F分别为BC,AD,EC的中点,且S△ABC=12,
则图中阴影部分的面积为(
C
)
A.1
B.2???????C.3
D.4
变式练习:
1.如图,在ΔABC中,D,E,F分别是AC,BD,AE的中点.若ΔDEF
的面积为1,则ΔABC的面积是(??C??)
A.3
B.4
C.8
D.12
2.如图,ΔABC三边上的中线AD,BE,CF交于点G.若S△ABC=24,则图中阴影部分的面积是__8
基础练习
1.如图,AD⊥BE,垂足为D,点C在BE上,以AD为高的三角形有(
A
)
A.6个
B.5个
C.4个
D.3个
1题
2题图
3题
2.如图,在ΔABC中,BC边上的高是AB,在ΔAEC中,AE边上的高是CD
3.如图,已知AD为ΔABC的中线,AB=12cm,AC=9cm,ΔACD的周长为27cm,则
ΔABD的周长为
30
cm.
4.已知AD是ΔABC的高,∠BAD=60°,∠CAD=20°,则∠BAC的度数为80°或40°
第5题
6题
7题
5.如图,D,E分别是ΔABC的边AB,BC上的点,AD=2BD,BE=CE.设ΔADF的面积
为S1,ΔCEF的面积为S2,若SΔABC=6,则S1-S2的值为1.
6.【教材变式】(P9第8题改)如图,在ΔABC中,AE,CD是ΔABC的两条高,AB=4,CD=2.
(1)请画出AE,CD;
(2)求ΔABC的面积;
(3)若AE=3,求BC的长.
解:(1)略;(2)4;(3).
7.如图,在ΔABC中,D,E,F分别为BC,AD,CE的中点,SΔABC=4,求SΔBEF.
解:易证SΔABD=SΔADc=2,S△AEC=SΔDEC=SΔBDE=1,SΔBEC=2,.SΔBEF=SΔBCF=1.
综合题探究
8.如图,在ΔABC中,AB>AC,AD为BC边上的中线.
(1)ΔABD的周长比ΔACD的周长大4.
①若AB=10,则AC=?6?;②若AB+AC=14,则AC=5;
(2)ΔABC的周长为27,AB=9,BC边上中线AD=6,ΔACD周长为19,求AC的长.
解:(1)①AC=6;②AB=9,AC=5;
(2)设AC=x,CD=y,:AD是BC边的中线,.BC=2CD=2y,
由题意得x+9+2y=27,x+6+y=19,解得x=8,y=5,..AC=8.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
