23.1.1 图形的旋转及性质同步练习(含答案)
文档属性
| 名称 | 23.1.1 图形的旋转及性质同步练习(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-15 13:32:21 | ||
图片预览


文档简介
23.1 图形的旋转
第1课时 图形的旋转及性质
一、选择题
1.下列运动形式属于旋转的是 ( )
A.放飞的风筝 B.飞奔的高铁动车
C.时钟上分针的运动 D.鱼在水中游动
2.如图,把△AOB绕点O顺时针旋转得到△COD,则旋转角是 ( )
A.∠AOC B.∠AOD C.∠AOB D.∠BOC
第2题图 第3题图 第4题图
3.如图,在4×4的正方形网格中,△PMN绕某点旋转一定的角度,得到△P1M1N1,其旋转中心是 ( )
A.点A B.点B C.点C D.点D
4.如图所示的每个小三角形是全等的等边三角形,其中的菱形AEFG可以看成是菱形ABCD以点A为中心 ( )
A.顺时针旋转60°所得到的
B.逆时针旋转60°所得到的
C.顺时针旋转120°所得到的
D.逆时针旋转120°所得到的
5.如图,将△ABC绕点C逆时针旋转60°得到△A'B'C,点A在边B'C上.若∠B=30°,则∠A'的大小是 ( )
A.30° B.60° C.90° D.120°
第5题图 第6题图 第7题图
6.如图,一块含30°角的直角三角板ABC绕点C顺时针旋转一定角度得到△A'B'C,当点B,C,A'在一条直线上时,三角板ABC的旋转角度为 ( )
A.150° B.120° C.60° D.30°
7.如图,将Rt△ABC绕点A顺时针旋转一定角度得到Rt△ADE,使得点B的对应点D恰好落在BC边上.若AB=1,∠B=60°,则CD的长为 ( )
A.0.5 B.1.5 C.2 D.1
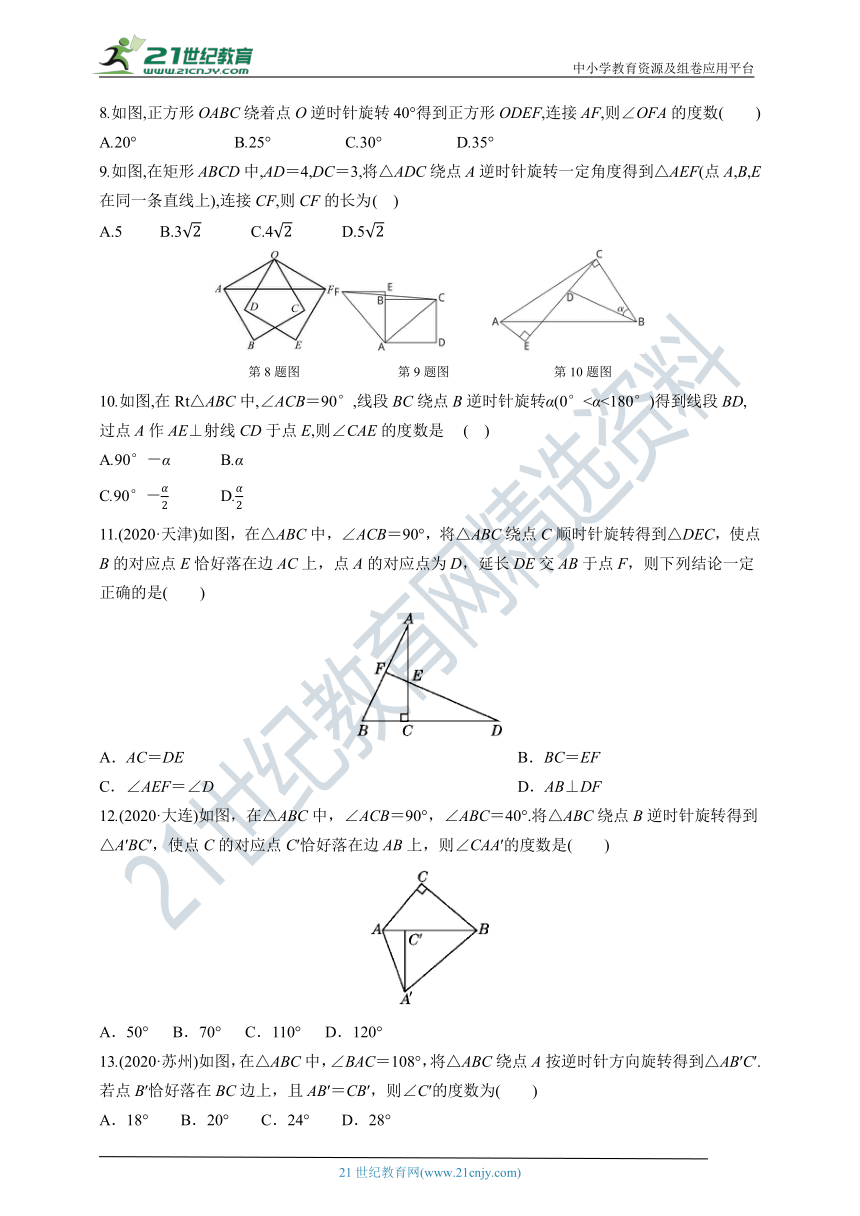
8.如图,正方形OABC绕着点O逆时针旋转40°得到正方形ODEF,连接AF,则∠OFA的度数( )
A.20° B.25° C.30° D.35°
9.如图,在矩形ABCD中,AD=4,DC=3,将△ADC绕点A逆时针旋转一定角度得到△AEF(点A,B,E在同一条直线上),连接CF,则CF的长为 ( )
A.5 B.32 C.42 D.52
第8题图 第9题图 第10题图
10.如图,在Rt△ABC中,∠ACB=90°,线段BC绕点B逆时针旋转α(0°<α<180°)得到线段BD,过点A作AE⊥射线CD于点E,则∠CAE的度数是 ( )
A.90°-α B.α
C.90°-α2 D.α2
11.(2020·天津)如图,在△ABC中,∠ACB=90°,将△ABC绕点C顺时针旋转得到△DEC,使点B的对应点E恰好落在边AC上,点A的对应点为D,延长DE交AB于点F,则下列结论一定正确的是( )
A.AC=DE B.BC=EF
C.∠AEF=∠D D.AB⊥DF
12.(2020·大连)如图,在△ABC中,∠ACB=90°,∠ABC=40°.将△ABC绕点B逆时针旋转得到△A′BC′,使点C的对应点C′恰好落在边AB上,则∠CAA′的度数是( )
A.50° B.70° C.110° D.120°
13.(2020·苏州)如图,在△ABC中,∠BAC=108°,将△ABC绕点A按逆时针方向旋转得到△AB′C′.若点B′恰好落在BC边上,且AB′=CB′,则∠C′的度数为( )
A.18° B.20° C.24° D.28°
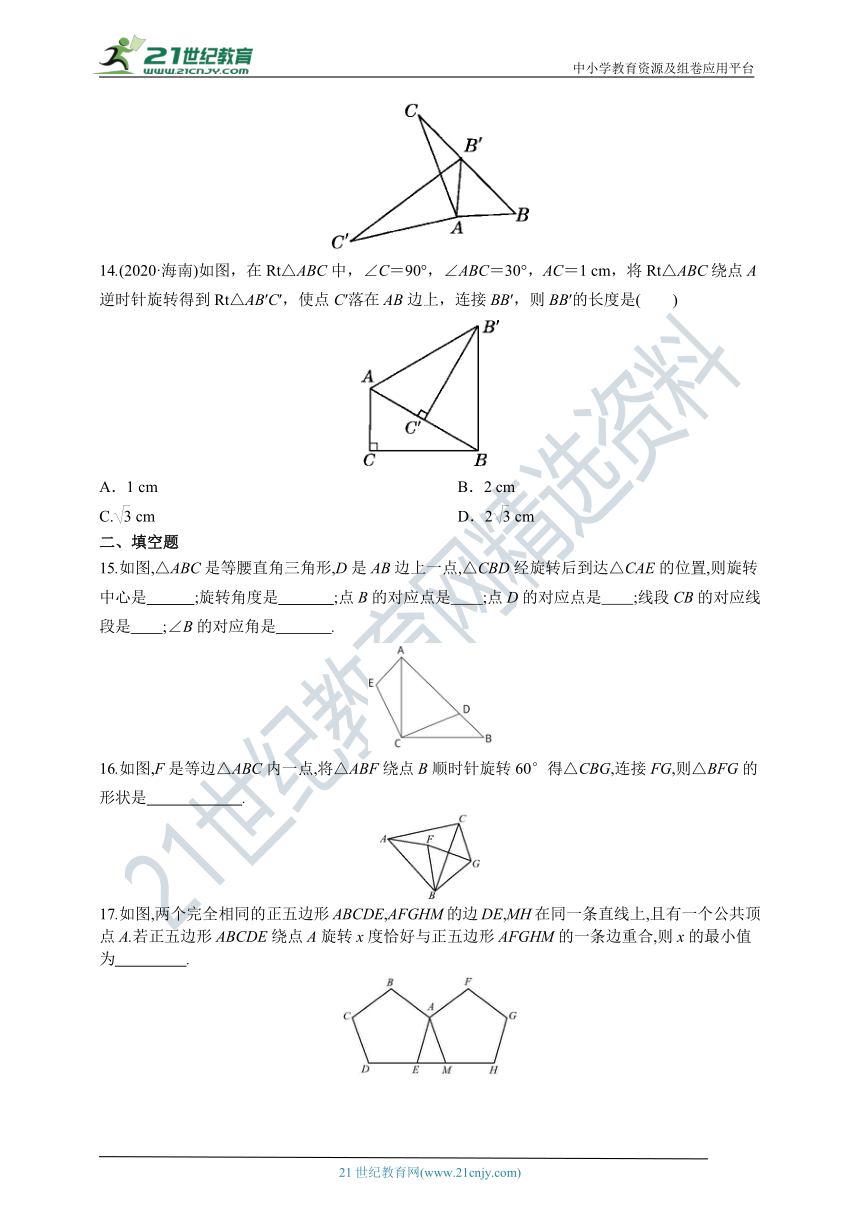
14.(2020·海南)如图,在Rt△ABC中,∠C=90°,∠ABC=30°,AC=1 cm,将Rt△ABC绕点A逆时针旋转得到Rt△AB′C′,使点C′落在AB边上,连接BB′,则BB′的长度是( )
A.1 cm B.2 cm
C. cm D.2 cm
二、填空题
15.如图,△ABC是等腰直角三角形,D是AB边上一点,△CBD经旋转后到达△CAE的位置,则旋转中心是 ;旋转角度是 ;点B的对应点是 ;点D的对应点是 ;线段CB的对应线段是 ;∠B的对应角是 .?
16.如图,F是等边△ABC内一点,将△ABF绕点B顺时针旋转60°得△CBG,连接FG,则△BFG的形状是 .?
17.如图,两个完全相同的正五边形ABCDE,AFGHM的边DE,MH在同一条直线上,且有一个公共顶点A.若正五边形ABCDE绕点A旋转x度恰好与正五边形AFGHM的一条边重合,则x的最小值为 .?
18.如图,正方形ABCD的边长为5,O是AB边的中点,E是正方形内的一个动点,OE=2,将线段CE绕点C逆时针旋转90°得到CF,连接OF,则线段OF的最小值为 .?
三、解答题
19.如图,在△ABC中,AB=AC,∠BAC=100°,将△ABC绕点A逆时针旋转40°得到△ADE,BC与AD,DE分别交于点G,F.
(1)求∠AGC的度数;
(2)求证:四边形ABFE是菱形.
20.如图,在Rt△ABC中,∠ACB=90°,点D,E分别在AB,AC上,EC=BC,连接CD,将线段CD绕点C顺时针旋转90°得到线段CF,连接EF.
(1)补全图形;
(2)若EF∥CD,求证:∠BDC=90°.
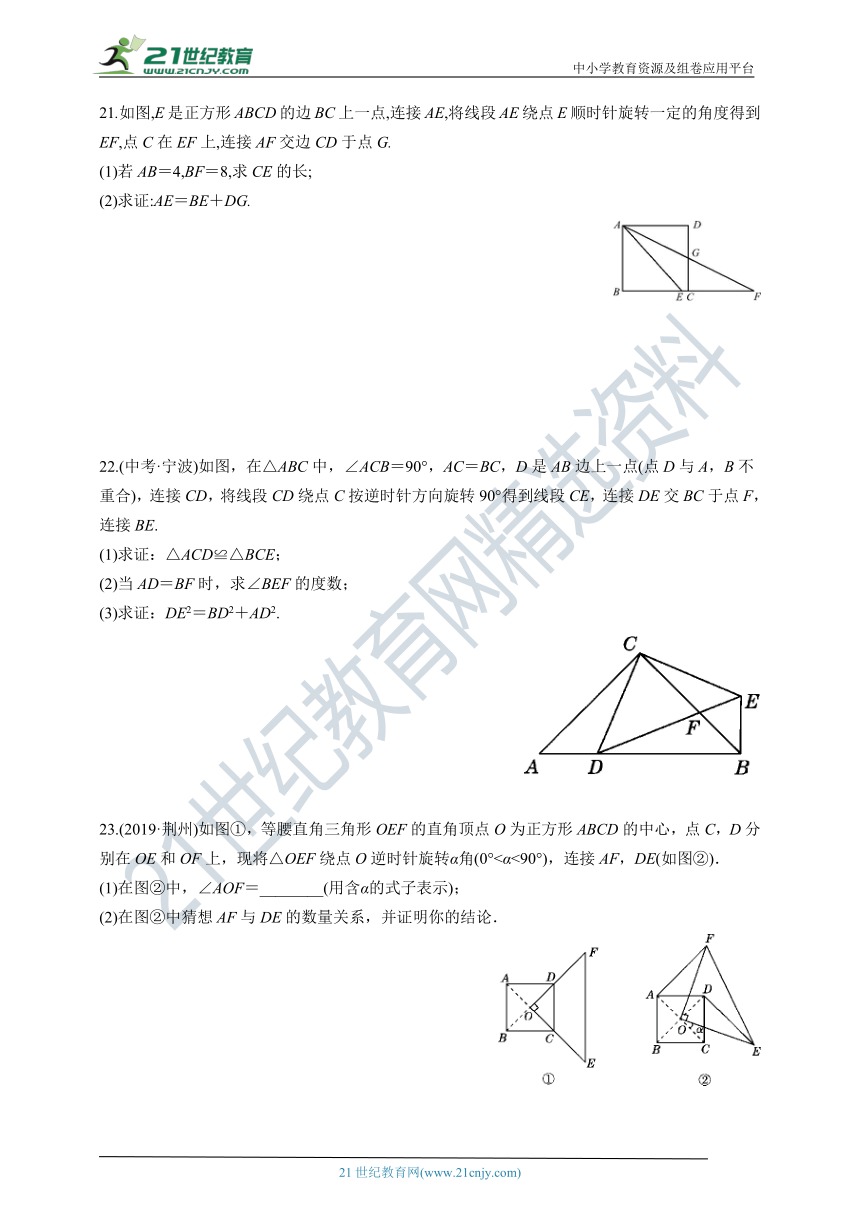
21.如图,E是正方形ABCD的边BC上一点,连接AE,将线段AE绕点E顺时针旋转一定的角度得到EF,点C在EF上,连接AF交边CD于点G.
(1)若AB=4,BF=8,求CE的长;
(2)求证:AE=BE+DG.
22.(中考·宁波)如图,在△ABC中,∠ACB=90°,AC=BC,D是AB边上一点(点D与A,B不重合),连接CD,将线段CD绕点C按逆时针方向旋转90°得到线段CE,连接DE交BC于点F,连接BE.
(1)求证:△ACD≌△BCE;
(2)当AD=BF时,求∠BEF的度数;
(3)求证:DE2=BD2+AD2.
23.(2019·荆州)如图①,等腰直角三角形OEF的直角顶点O为正方形ABCD的中心,点C,D分别在OE和OF上,现将△OEF绕点O逆时针旋转α角(0°<α<90°),连接AF,DE(如图②).
(1)在图②中,∠AOF=________(用含α的式子表示);
(2)在图②中猜想AF与DE的数量关系,并证明你的结论.
24.【探索新知】
如图1,射线OC在∠AOB的内部,图中共有3个角:∠AOB,∠AOC和∠BOC,若其中有一个角的度数是另一个角度数的两倍,则称射线OC是∠AOB的“巧分线”.
(1)一个角的平分线 这个角的“巧分线”;(填“是”或“不是”)?
(2)如图2,若∠MPN=α,且射线PQ是∠MPN的“巧分线”,则∠MPQ= .(用含α的代数式表示出所有可能的结果)?
【深入研究】
如图2,若∠MPN=60°,且射线PQ绕点P从PN位置开始,以每秒10°的速度逆时针旋转,当PQ与PN成180°时停止旋转,旋转的时间为t秒.
(3)当t为何值时,射线PM是∠QPN的“巧分线”?
(4)若射线PM同时绕点P以每秒5°的速度逆时针旋转,并与PQ同时停止,请直接写出当射线PQ是∠MPN的“巧分线”时t的值.
参考答案
一、选择题
1.下列运动形式属于旋转的是 (C)
A.放飞的风筝 B.飞奔的高铁动车
C.时钟上分针的运动 D.鱼在水中游动
2.如图,把△AOB绕点O顺时针旋转得到△COD,则旋转角是 (A)
A.∠AOC B.∠AOD C.∠AOB D.∠BOC
第2题图 第3题图 第4题图
3.如图,在4×4的正方形网格中,△PMN绕某点旋转一定的角度,得到△P1M1N1,其旋转中心是 (B)
A.点A B.点B C.点C D.点D
4.如图所示的每个小三角形是全等的等边三角形,其中的菱形AEFG可以看成是菱形ABCD以点A为中心 (D)
A.顺时针旋转60°所得到的
B.逆时针旋转60°所得到的
C.顺时针旋转120°所得到的
D.逆时针旋转120°所得到的
5.如图,将△ABC绕点C逆时针旋转60°得到△A'B'C,点A在边B'C上.若∠B=30°,则∠A'的大小是 (C)
A.30° B.60° C.90° D.120°
第5题图 第6题图 第7题图
6.如图,一块含30°角的直角三角板ABC绕点C顺时针旋转一定角度得到△A'B'C,当点B,C,A'在一条直线上时,三角板ABC的旋转角度为 (A)
A.150° B.120° C.60° D.30°
7.如图,将Rt△ABC绕点A顺时针旋转一定角度得到Rt△ADE,使得点B的对应点D恰好落在BC边上.若AB=1,∠B=60°,则CD的长为 (D)
A.0.5 B.1.5 C.2 D.1
8.如图,正方形OABC绕着点O逆时针旋转40°得到正方形ODEF,连接AF,则∠OFA的度数( B )
A.20° B.25° C.30° D.35°
9.如图,在矩形ABCD中,AD=4,DC=3,将△ADC绕点A逆时针旋转一定角度得到△AEF(点A,B,E在同一条直线上),连接CF,则CF的长为 (D)
A.5 B.32 C.42 D.52
第8题图 第9题图 第10题图
10.如图,在Rt△ABC中,∠ACB=90°,线段BC绕点B逆时针旋转α(0°<α<180°)得到线段BD,过点A作AE⊥射线CD于点E,则∠CAE的度数是 (C)
A.90°-α B.α
C.90°-α2 D.α2
11.(2020·天津)如图,在△ABC中,∠ACB=90°,将△ABC绕点C顺时针旋转得到△DEC,使点B的对应点E恰好落在边AC上,点A的对应点为D,延长DE交AB于点F,则下列结论一定正确的是( D )
A.AC=DE B.BC=EF
C.∠AEF=∠D D.AB⊥DF
12.(2020·大连)如图,在△ABC中,∠ACB=90°,∠ABC=40°.将△ABC绕点B逆时针旋转得到△A′BC′,使点C的对应点C′恰好落在边AB上,则∠CAA′的度数是( D )
A.50° B.70° C.110° D.120°
13.(2020·苏州)如图,在△ABC中,∠BAC=108°,将△ABC绕点A按逆时针方向旋转得到△AB′C′.若点B′恰好落在BC边上,且AB′=CB′,则∠C′的度数为( C )
A.18° B.20° C.24° D.28°
14.(2020·海南)如图,在Rt△ABC中,∠C=90°,∠ABC=30°,AC=1 cm,将Rt△ABC绕点A逆时针旋转得到Rt△AB′C′,使点C′落在AB边上,连接BB′,则BB′的长度是( B )
A.1 cm B.2 cm
C. cm D.2 cm
二、填空题
15.如图,△ABC是等腰直角三角形,D是AB边上一点,△CBD经旋转后到达△CAE的位置,则旋转中心是 点C ;旋转角度是 90° ;点B的对应点是 A ;点D的对应点是 E ;线段CB的对应线段是 CA ;∠B的对应角是 ∠CAE .?
16.如图,F是等边△ABC内一点,将△ABF绕点B顺时针旋转60°得△CBG,连接FG,则△BFG的形状是 等边三角形 .?
17.如图,两个完全相同的正五边形ABCDE,AFGHM的边DE,MH在同一条直线上,且有一个公共顶点A.若正五边形ABCDE绕点A旋转x度恰好与正五边形AFGHM的一条边重合,则x的最小值为 36 .?
18.如图,正方形ABCD的边长为5,O是AB边的中点,E是正方形内的一个动点,OE=2,将线段CE绕点C逆时针旋转90°得到CF,连接OF,则线段OF的最小值为?5102-2 .?
提示:如图,连接CO,将线段CO绕点C逆时针旋转90°得到CM,连接FM,OM,∴∠ECF=∠OCM=90°,∴∠ECO=∠FCM.∵CE=CF,CO=CM,∴△ECO≌△FCM(SAS),∴FM=OE=2.∵正方形ABCD中,AB=5,O是AB边的中点,∴OB=2.5,∴OC=52+522=552,∴OM=2OC=5102.∵OF+MF≥OM,∴OF≥5102-2,∴线段OF的最小值为5102-2.
三、解答题
19.如图,在△ABC中,AB=AC,∠BAC=100°,将△ABC绕点A逆时针旋转40°得到△ADE,BC与AD,DE分别交于点G,F.
(1)求∠AGC的度数;
(2)求证:四边形ABFE是菱形.
解:(1)∵AB=AC,∠BAC=100°,
∴∠B=∠C=40°.
由旋转的性质可知∠BAD=40°,
∴∠AGC=∠B+∠BAD=80°.
(2)由旋转的性质可知∠D=∠B=∠BAD=40°,
∠DAE=100°,∴AB∥DE.
由(1)知∠AGC=80°,∴∠DAE+∠AGC=180°,∴AE∥BF,
∴四边形ABFE是平行四边形.
又∵AB=AC=AE,∴四边形ABFE是菱形.
20.如图,在Rt△ABC中,∠ACB=90°,点D,E分别在AB,AC上,EC=BC,连接CD,将线段CD绕点C顺时针旋转90°得到线段CF,连接EF.
(1)补全图形;
(2)若EF∥CD,求证:∠BDC=90°.
解:(1)补全图形,如图所示.
(2)由旋转的性质可知∠DCF=∠DCE+∠ECF=90°,CD=CF.
∵∠ACB=∠DCE+∠BCD=90°,
∴∠ECF=∠BCD.
∵EF∥CD,∴∠EFC+∠DCF=180°,
∴∠EFC=90°.
在△BDC和△EFC中,CD=CF,∠BCD=∠ECF,BC=EC,
∴△BDC≌△EFC(SAS),
∴∠BDC=∠EFC=90°.
21.如图,E是正方形ABCD的边BC上一点,连接AE,将线段AE绕点E顺时针旋转一定的角度得到EF,点C在EF上,连接AF交边CD于点G.
(1)若AB=4,BF=8,求CE的长;
(2)求证:AE=BE+DG.
解:(1)∵四边形ABCD为正方形,
∴AB=BC=4,∠ABC=90°.
∵BF=8,∴CF=BF-BC=4.
由旋转的性质知,EF=AE,
∴BE=BF-EF=BF-AE=8-AE,
在Rt△ABE中,AB2+BE2=AE2,
即42+(8-AE)2=AE2,解得AE=5,
∴CE=EF-CF=AE-CF=5-4=1.
(2)延长EB到点H,使得BH=DG,
易证△ADG≌△ABH(AAS),
∴∠BAH=∠DAG,∴∠HAF=∠BAD=90°.
∵AE=EF,∴∠EAF=∠F.
∵∠EAH+∠EAF=90°,∠F+∠H=90°,
∴∠H=∠EAH,∴EA=EH.
∵EH=BE+BH=BE+DG,
∴AE=BE+BG.
22.(中考·宁波)如图,在△ABC中,∠ACB=90°,AC=BC,D是AB边上一点(点D与A,B不重合),连接CD,将线段CD绕点C按逆时针方向旋转90°得到线段CE,连接DE交BC于点F,连接BE.
(1)求证:△ACD≌△BCE;
证明:由题意可知CD=CE,∠DCE=90°.
∵∠ACB=90°,∴∠DCE=∠ACB.
∵∠ACD=∠ACB-∠DCB,∠BCE=∠DCE-∠DCB,
∴∠ACD=∠BCE.
在△ACD和△BCE中,
∴△ACD≌△BCE(SAS).
(2)当AD=BF时,求∠BEF的度数;
解:∵∠ACB=90°,AC=BC,∴∠A=45°.
由(1)知△ACD≌△BCE,
∴∠A=∠CBE=45°,AD=BE.
∵AD=BF,∴BE=BF.
∴∠BEF==67.5°.
(3)求证:DE2=BD2+AD2.
证明:由(1)知△ACD≌△BCE,∴∠A=∠CBE,AD=BE.
∵∠ACB=90°,∴∠A+∠CBA=90°.
∴∠CBE+∠CBA=90°.
∴∠EBD=90°.
∴DE2=BD2+BE2.
∴DE2=BD2+AD2.
23.(2019·荆州)如图①,等腰直角三角形OEF的直角顶点O为正方形ABCD的中心,点C,D分别在OE和OF上,现将△OEF绕点O逆时针旋转α角(0°<α<90°),连接AF,DE(如图②).
(1)在图②中,∠AOF=________(用含α的式子表示);
【思路点拨】如图②,利用旋转的性质得到∠DOF=∠COE=α,再根据正方形的性质得到∠AOD=90°,从而得到∠AOF=90°-α;
(2)在图②中猜想AF与DE的数量关系,并证明你的结论.
【思路点拨】如图②,利用正方形的性质得到∠AOD=∠COD=90°,OA=OD,再利用△OEF为等腰直角三角形得到OF=OE,利用(1)的结论得到∠AOF=∠DOE,则可证明△AOF≌△DOE,从而得到AF=DE.
解:AF=DE.证明如下:
∵四边形ABCD为正方形,∴∠AOD=∠COD=90°,OA=OD.
∵∠DOF=∠COE=α.∴∠AOF=∠DOE.
∵△OEF为等腰直角三角形,∴OF=OE.
在△AOF和△DOE中,
∴△AOF≌△DOE(SAS).∴AF=DE.
24.【探索新知】
如图1,射线OC在∠AOB的内部,图中共有3个角:∠AOB,∠AOC和∠BOC,若其中有一个角的度数是另一个角度数的两倍,则称射线OC是∠AOB的“巧分线”.
(1)一个角的平分线 是 这个角的“巧分线”;(填“是”或“不是”)?
(2)如图2,若∠MPN=α,且射线PQ是∠MPN的“巧分线”,则∠MPQ=?12α或13α或23α .(用含α的代数式表示出所有可能的结果)?
【深入研究】
如图2,若∠MPN=60°,且射线PQ绕点P从PN位置开始,以每秒10°的速度逆时针旋转,当PQ与PN成180°时停止旋转,旋转的时间为t秒.
(3)当t为何值时,射线PM是∠QPN的“巧分线”?
(4)若射线PM同时绕点P以每秒5°的速度逆时针旋转,并与PQ同时停止,请直接写出当射线PQ是∠MPN的“巧分线”时t的值.
解:(3)依题意有①10t=60+12×60,解得t=9;
②10t=2×60,解得t=12;
③10t=60+2×60,解得t=18.
故当t为9或12或18时,射线PM是∠QPN的“巧分线”.
(4)当t为2.4或4或6时,射线PQ是∠MPN的“巧分线”.
提示:依题意有①10t=13(5t+60),解得t=2.4;
②10t=12(5t+60),解得t=4;
③10t=23(5t+60),解得t=6.
第1课时 图形的旋转及性质
一、选择题
1.下列运动形式属于旋转的是 ( )
A.放飞的风筝 B.飞奔的高铁动车
C.时钟上分针的运动 D.鱼在水中游动
2.如图,把△AOB绕点O顺时针旋转得到△COD,则旋转角是 ( )
A.∠AOC B.∠AOD C.∠AOB D.∠BOC
第2题图 第3题图 第4题图
3.如图,在4×4的正方形网格中,△PMN绕某点旋转一定的角度,得到△P1M1N1,其旋转中心是 ( )
A.点A B.点B C.点C D.点D
4.如图所示的每个小三角形是全等的等边三角形,其中的菱形AEFG可以看成是菱形ABCD以点A为中心 ( )
A.顺时针旋转60°所得到的
B.逆时针旋转60°所得到的
C.顺时针旋转120°所得到的
D.逆时针旋转120°所得到的
5.如图,将△ABC绕点C逆时针旋转60°得到△A'B'C,点A在边B'C上.若∠B=30°,则∠A'的大小是 ( )
A.30° B.60° C.90° D.120°
第5题图 第6题图 第7题图
6.如图,一块含30°角的直角三角板ABC绕点C顺时针旋转一定角度得到△A'B'C,当点B,C,A'在一条直线上时,三角板ABC的旋转角度为 ( )
A.150° B.120° C.60° D.30°
7.如图,将Rt△ABC绕点A顺时针旋转一定角度得到Rt△ADE,使得点B的对应点D恰好落在BC边上.若AB=1,∠B=60°,则CD的长为 ( )
A.0.5 B.1.5 C.2 D.1
8.如图,正方形OABC绕着点O逆时针旋转40°得到正方形ODEF,连接AF,则∠OFA的度数( )
A.20° B.25° C.30° D.35°
9.如图,在矩形ABCD中,AD=4,DC=3,将△ADC绕点A逆时针旋转一定角度得到△AEF(点A,B,E在同一条直线上),连接CF,则CF的长为 ( )
A.5 B.32 C.42 D.52
第8题图 第9题图 第10题图
10.如图,在Rt△ABC中,∠ACB=90°,线段BC绕点B逆时针旋转α(0°<α<180°)得到线段BD,过点A作AE⊥射线CD于点E,则∠CAE的度数是 ( )
A.90°-α B.α
C.90°-α2 D.α2
11.(2020·天津)如图,在△ABC中,∠ACB=90°,将△ABC绕点C顺时针旋转得到△DEC,使点B的对应点E恰好落在边AC上,点A的对应点为D,延长DE交AB于点F,则下列结论一定正确的是( )
A.AC=DE B.BC=EF
C.∠AEF=∠D D.AB⊥DF
12.(2020·大连)如图,在△ABC中,∠ACB=90°,∠ABC=40°.将△ABC绕点B逆时针旋转得到△A′BC′,使点C的对应点C′恰好落在边AB上,则∠CAA′的度数是( )
A.50° B.70° C.110° D.120°
13.(2020·苏州)如图,在△ABC中,∠BAC=108°,将△ABC绕点A按逆时针方向旋转得到△AB′C′.若点B′恰好落在BC边上,且AB′=CB′,则∠C′的度数为( )
A.18° B.20° C.24° D.28°
14.(2020·海南)如图,在Rt△ABC中,∠C=90°,∠ABC=30°,AC=1 cm,将Rt△ABC绕点A逆时针旋转得到Rt△AB′C′,使点C′落在AB边上,连接BB′,则BB′的长度是( )
A.1 cm B.2 cm
C. cm D.2 cm
二、填空题
15.如图,△ABC是等腰直角三角形,D是AB边上一点,△CBD经旋转后到达△CAE的位置,则旋转中心是 ;旋转角度是 ;点B的对应点是 ;点D的对应点是 ;线段CB的对应线段是 ;∠B的对应角是 .?
16.如图,F是等边△ABC内一点,将△ABF绕点B顺时针旋转60°得△CBG,连接FG,则△BFG的形状是 .?
17.如图,两个完全相同的正五边形ABCDE,AFGHM的边DE,MH在同一条直线上,且有一个公共顶点A.若正五边形ABCDE绕点A旋转x度恰好与正五边形AFGHM的一条边重合,则x的最小值为 .?
18.如图,正方形ABCD的边长为5,O是AB边的中点,E是正方形内的一个动点,OE=2,将线段CE绕点C逆时针旋转90°得到CF,连接OF,则线段OF的最小值为 .?
三、解答题
19.如图,在△ABC中,AB=AC,∠BAC=100°,将△ABC绕点A逆时针旋转40°得到△ADE,BC与AD,DE分别交于点G,F.
(1)求∠AGC的度数;
(2)求证:四边形ABFE是菱形.
20.如图,在Rt△ABC中,∠ACB=90°,点D,E分别在AB,AC上,EC=BC,连接CD,将线段CD绕点C顺时针旋转90°得到线段CF,连接EF.
(1)补全图形;
(2)若EF∥CD,求证:∠BDC=90°.
21.如图,E是正方形ABCD的边BC上一点,连接AE,将线段AE绕点E顺时针旋转一定的角度得到EF,点C在EF上,连接AF交边CD于点G.
(1)若AB=4,BF=8,求CE的长;
(2)求证:AE=BE+DG.
22.(中考·宁波)如图,在△ABC中,∠ACB=90°,AC=BC,D是AB边上一点(点D与A,B不重合),连接CD,将线段CD绕点C按逆时针方向旋转90°得到线段CE,连接DE交BC于点F,连接BE.
(1)求证:△ACD≌△BCE;
(2)当AD=BF时,求∠BEF的度数;
(3)求证:DE2=BD2+AD2.
23.(2019·荆州)如图①,等腰直角三角形OEF的直角顶点O为正方形ABCD的中心,点C,D分别在OE和OF上,现将△OEF绕点O逆时针旋转α角(0°<α<90°),连接AF,DE(如图②).
(1)在图②中,∠AOF=________(用含α的式子表示);
(2)在图②中猜想AF与DE的数量关系,并证明你的结论.
24.【探索新知】
如图1,射线OC在∠AOB的内部,图中共有3个角:∠AOB,∠AOC和∠BOC,若其中有一个角的度数是另一个角度数的两倍,则称射线OC是∠AOB的“巧分线”.
(1)一个角的平分线 这个角的“巧分线”;(填“是”或“不是”)?
(2)如图2,若∠MPN=α,且射线PQ是∠MPN的“巧分线”,则∠MPQ= .(用含α的代数式表示出所有可能的结果)?
【深入研究】
如图2,若∠MPN=60°,且射线PQ绕点P从PN位置开始,以每秒10°的速度逆时针旋转,当PQ与PN成180°时停止旋转,旋转的时间为t秒.
(3)当t为何值时,射线PM是∠QPN的“巧分线”?
(4)若射线PM同时绕点P以每秒5°的速度逆时针旋转,并与PQ同时停止,请直接写出当射线PQ是∠MPN的“巧分线”时t的值.
参考答案
一、选择题
1.下列运动形式属于旋转的是 (C)
A.放飞的风筝 B.飞奔的高铁动车
C.时钟上分针的运动 D.鱼在水中游动
2.如图,把△AOB绕点O顺时针旋转得到△COD,则旋转角是 (A)
A.∠AOC B.∠AOD C.∠AOB D.∠BOC
第2题图 第3题图 第4题图
3.如图,在4×4的正方形网格中,△PMN绕某点旋转一定的角度,得到△P1M1N1,其旋转中心是 (B)
A.点A B.点B C.点C D.点D
4.如图所示的每个小三角形是全等的等边三角形,其中的菱形AEFG可以看成是菱形ABCD以点A为中心 (D)
A.顺时针旋转60°所得到的
B.逆时针旋转60°所得到的
C.顺时针旋转120°所得到的
D.逆时针旋转120°所得到的
5.如图,将△ABC绕点C逆时针旋转60°得到△A'B'C,点A在边B'C上.若∠B=30°,则∠A'的大小是 (C)
A.30° B.60° C.90° D.120°
第5题图 第6题图 第7题图
6.如图,一块含30°角的直角三角板ABC绕点C顺时针旋转一定角度得到△A'B'C,当点B,C,A'在一条直线上时,三角板ABC的旋转角度为 (A)
A.150° B.120° C.60° D.30°
7.如图,将Rt△ABC绕点A顺时针旋转一定角度得到Rt△ADE,使得点B的对应点D恰好落在BC边上.若AB=1,∠B=60°,则CD的长为 (D)
A.0.5 B.1.5 C.2 D.1
8.如图,正方形OABC绕着点O逆时针旋转40°得到正方形ODEF,连接AF,则∠OFA的度数( B )
A.20° B.25° C.30° D.35°
9.如图,在矩形ABCD中,AD=4,DC=3,将△ADC绕点A逆时针旋转一定角度得到△AEF(点A,B,E在同一条直线上),连接CF,则CF的长为 (D)
A.5 B.32 C.42 D.52
第8题图 第9题图 第10题图
10.如图,在Rt△ABC中,∠ACB=90°,线段BC绕点B逆时针旋转α(0°<α<180°)得到线段BD,过点A作AE⊥射线CD于点E,则∠CAE的度数是 (C)
A.90°-α B.α
C.90°-α2 D.α2
11.(2020·天津)如图,在△ABC中,∠ACB=90°,将△ABC绕点C顺时针旋转得到△DEC,使点B的对应点E恰好落在边AC上,点A的对应点为D,延长DE交AB于点F,则下列结论一定正确的是( D )
A.AC=DE B.BC=EF
C.∠AEF=∠D D.AB⊥DF
12.(2020·大连)如图,在△ABC中,∠ACB=90°,∠ABC=40°.将△ABC绕点B逆时针旋转得到△A′BC′,使点C的对应点C′恰好落在边AB上,则∠CAA′的度数是( D )
A.50° B.70° C.110° D.120°
13.(2020·苏州)如图,在△ABC中,∠BAC=108°,将△ABC绕点A按逆时针方向旋转得到△AB′C′.若点B′恰好落在BC边上,且AB′=CB′,则∠C′的度数为( C )
A.18° B.20° C.24° D.28°
14.(2020·海南)如图,在Rt△ABC中,∠C=90°,∠ABC=30°,AC=1 cm,将Rt△ABC绕点A逆时针旋转得到Rt△AB′C′,使点C′落在AB边上,连接BB′,则BB′的长度是( B )
A.1 cm B.2 cm
C. cm D.2 cm
二、填空题
15.如图,△ABC是等腰直角三角形,D是AB边上一点,△CBD经旋转后到达△CAE的位置,则旋转中心是 点C ;旋转角度是 90° ;点B的对应点是 A ;点D的对应点是 E ;线段CB的对应线段是 CA ;∠B的对应角是 ∠CAE .?
16.如图,F是等边△ABC内一点,将△ABF绕点B顺时针旋转60°得△CBG,连接FG,则△BFG的形状是 等边三角形 .?
17.如图,两个完全相同的正五边形ABCDE,AFGHM的边DE,MH在同一条直线上,且有一个公共顶点A.若正五边形ABCDE绕点A旋转x度恰好与正五边形AFGHM的一条边重合,则x的最小值为 36 .?
18.如图,正方形ABCD的边长为5,O是AB边的中点,E是正方形内的一个动点,OE=2,将线段CE绕点C逆时针旋转90°得到CF,连接OF,则线段OF的最小值为?5102-2 .?
提示:如图,连接CO,将线段CO绕点C逆时针旋转90°得到CM,连接FM,OM,∴∠ECF=∠OCM=90°,∴∠ECO=∠FCM.∵CE=CF,CO=CM,∴△ECO≌△FCM(SAS),∴FM=OE=2.∵正方形ABCD中,AB=5,O是AB边的中点,∴OB=2.5,∴OC=52+522=552,∴OM=2OC=5102.∵OF+MF≥OM,∴OF≥5102-2,∴线段OF的最小值为5102-2.
三、解答题
19.如图,在△ABC中,AB=AC,∠BAC=100°,将△ABC绕点A逆时针旋转40°得到△ADE,BC与AD,DE分别交于点G,F.
(1)求∠AGC的度数;
(2)求证:四边形ABFE是菱形.
解:(1)∵AB=AC,∠BAC=100°,
∴∠B=∠C=40°.
由旋转的性质可知∠BAD=40°,
∴∠AGC=∠B+∠BAD=80°.
(2)由旋转的性质可知∠D=∠B=∠BAD=40°,
∠DAE=100°,∴AB∥DE.
由(1)知∠AGC=80°,∴∠DAE+∠AGC=180°,∴AE∥BF,
∴四边形ABFE是平行四边形.
又∵AB=AC=AE,∴四边形ABFE是菱形.
20.如图,在Rt△ABC中,∠ACB=90°,点D,E分别在AB,AC上,EC=BC,连接CD,将线段CD绕点C顺时针旋转90°得到线段CF,连接EF.
(1)补全图形;
(2)若EF∥CD,求证:∠BDC=90°.
解:(1)补全图形,如图所示.
(2)由旋转的性质可知∠DCF=∠DCE+∠ECF=90°,CD=CF.
∵∠ACB=∠DCE+∠BCD=90°,
∴∠ECF=∠BCD.
∵EF∥CD,∴∠EFC+∠DCF=180°,
∴∠EFC=90°.
在△BDC和△EFC中,CD=CF,∠BCD=∠ECF,BC=EC,
∴△BDC≌△EFC(SAS),
∴∠BDC=∠EFC=90°.
21.如图,E是正方形ABCD的边BC上一点,连接AE,将线段AE绕点E顺时针旋转一定的角度得到EF,点C在EF上,连接AF交边CD于点G.
(1)若AB=4,BF=8,求CE的长;
(2)求证:AE=BE+DG.
解:(1)∵四边形ABCD为正方形,
∴AB=BC=4,∠ABC=90°.
∵BF=8,∴CF=BF-BC=4.
由旋转的性质知,EF=AE,
∴BE=BF-EF=BF-AE=8-AE,
在Rt△ABE中,AB2+BE2=AE2,
即42+(8-AE)2=AE2,解得AE=5,
∴CE=EF-CF=AE-CF=5-4=1.
(2)延长EB到点H,使得BH=DG,
易证△ADG≌△ABH(AAS),
∴∠BAH=∠DAG,∴∠HAF=∠BAD=90°.
∵AE=EF,∴∠EAF=∠F.
∵∠EAH+∠EAF=90°,∠F+∠H=90°,
∴∠H=∠EAH,∴EA=EH.
∵EH=BE+BH=BE+DG,
∴AE=BE+BG.
22.(中考·宁波)如图,在△ABC中,∠ACB=90°,AC=BC,D是AB边上一点(点D与A,B不重合),连接CD,将线段CD绕点C按逆时针方向旋转90°得到线段CE,连接DE交BC于点F,连接BE.
(1)求证:△ACD≌△BCE;
证明:由题意可知CD=CE,∠DCE=90°.
∵∠ACB=90°,∴∠DCE=∠ACB.
∵∠ACD=∠ACB-∠DCB,∠BCE=∠DCE-∠DCB,
∴∠ACD=∠BCE.
在△ACD和△BCE中,
∴△ACD≌△BCE(SAS).
(2)当AD=BF时,求∠BEF的度数;
解:∵∠ACB=90°,AC=BC,∴∠A=45°.
由(1)知△ACD≌△BCE,
∴∠A=∠CBE=45°,AD=BE.
∵AD=BF,∴BE=BF.
∴∠BEF==67.5°.
(3)求证:DE2=BD2+AD2.
证明:由(1)知△ACD≌△BCE,∴∠A=∠CBE,AD=BE.
∵∠ACB=90°,∴∠A+∠CBA=90°.
∴∠CBE+∠CBA=90°.
∴∠EBD=90°.
∴DE2=BD2+BE2.
∴DE2=BD2+AD2.
23.(2019·荆州)如图①,等腰直角三角形OEF的直角顶点O为正方形ABCD的中心,点C,D分别在OE和OF上,现将△OEF绕点O逆时针旋转α角(0°<α<90°),连接AF,DE(如图②).
(1)在图②中,∠AOF=________(用含α的式子表示);
【思路点拨】如图②,利用旋转的性质得到∠DOF=∠COE=α,再根据正方形的性质得到∠AOD=90°,从而得到∠AOF=90°-α;
(2)在图②中猜想AF与DE的数量关系,并证明你的结论.
【思路点拨】如图②,利用正方形的性质得到∠AOD=∠COD=90°,OA=OD,再利用△OEF为等腰直角三角形得到OF=OE,利用(1)的结论得到∠AOF=∠DOE,则可证明△AOF≌△DOE,从而得到AF=DE.
解:AF=DE.证明如下:
∵四边形ABCD为正方形,∴∠AOD=∠COD=90°,OA=OD.
∵∠DOF=∠COE=α.∴∠AOF=∠DOE.
∵△OEF为等腰直角三角形,∴OF=OE.
在△AOF和△DOE中,
∴△AOF≌△DOE(SAS).∴AF=DE.
24.【探索新知】
如图1,射线OC在∠AOB的内部,图中共有3个角:∠AOB,∠AOC和∠BOC,若其中有一个角的度数是另一个角度数的两倍,则称射线OC是∠AOB的“巧分线”.
(1)一个角的平分线 是 这个角的“巧分线”;(填“是”或“不是”)?
(2)如图2,若∠MPN=α,且射线PQ是∠MPN的“巧分线”,则∠MPQ=?12α或13α或23α .(用含α的代数式表示出所有可能的结果)?
【深入研究】
如图2,若∠MPN=60°,且射线PQ绕点P从PN位置开始,以每秒10°的速度逆时针旋转,当PQ与PN成180°时停止旋转,旋转的时间为t秒.
(3)当t为何值时,射线PM是∠QPN的“巧分线”?
(4)若射线PM同时绕点P以每秒5°的速度逆时针旋转,并与PQ同时停止,请直接写出当射线PQ是∠MPN的“巧分线”时t的值.
解:(3)依题意有①10t=60+12×60,解得t=9;
②10t=2×60,解得t=12;
③10t=60+2×60,解得t=18.
故当t为9或12或18时,射线PM是∠QPN的“巧分线”.
(4)当t为2.4或4或6时,射线PQ是∠MPN的“巧分线”.
提示:依题意有①10t=13(5t+60),解得t=2.4;
②10t=12(5t+60),解得t=4;
③10t=23(5t+60),解得t=6.
同课章节目录
