23.2.2 中心对称图形同步练习(含答案)
文档属性
| 名称 | 23.2.2 中心对称图形同步练习(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-15 13:38:14 | ||
图片预览



文档简介
23.2 中心对称
23.2.2 中心对称图形
一、选择题
1.下列图形是我国国产品牌汽车的标识,这些汽车标识中,是中心对称图形的是 ( )
2.下列手机手势解锁图案中,是中心对称图形的是 ( )
3.下列图形中,既是轴对称图形,又是中心对称图形的是 ( )
4.(2020·遂宁)下列图形中,既是轴对称图形,又是中心对称图形的是( )
A.等边三角形 B.平行四边形 C.矩形 D.正五边形
5.如图,该图形是中心对称图形,则对称中心是 ( )
A.点C B.点D C.线段BC的中点 D.线段FC的中点
6.如图,△ABC是一个中心对称图形的一部分,点O是对称中心,A和B是对应点,∠C=90°,那么将这个图形补充完整后是 ( )
A.矩形 B.菱形 C.正方形 D.梯形
7.(中考·宜昌)如图,若要添加一条线段,使之既是轴对称图形又是中心对称图形,正确的添加位置是( )
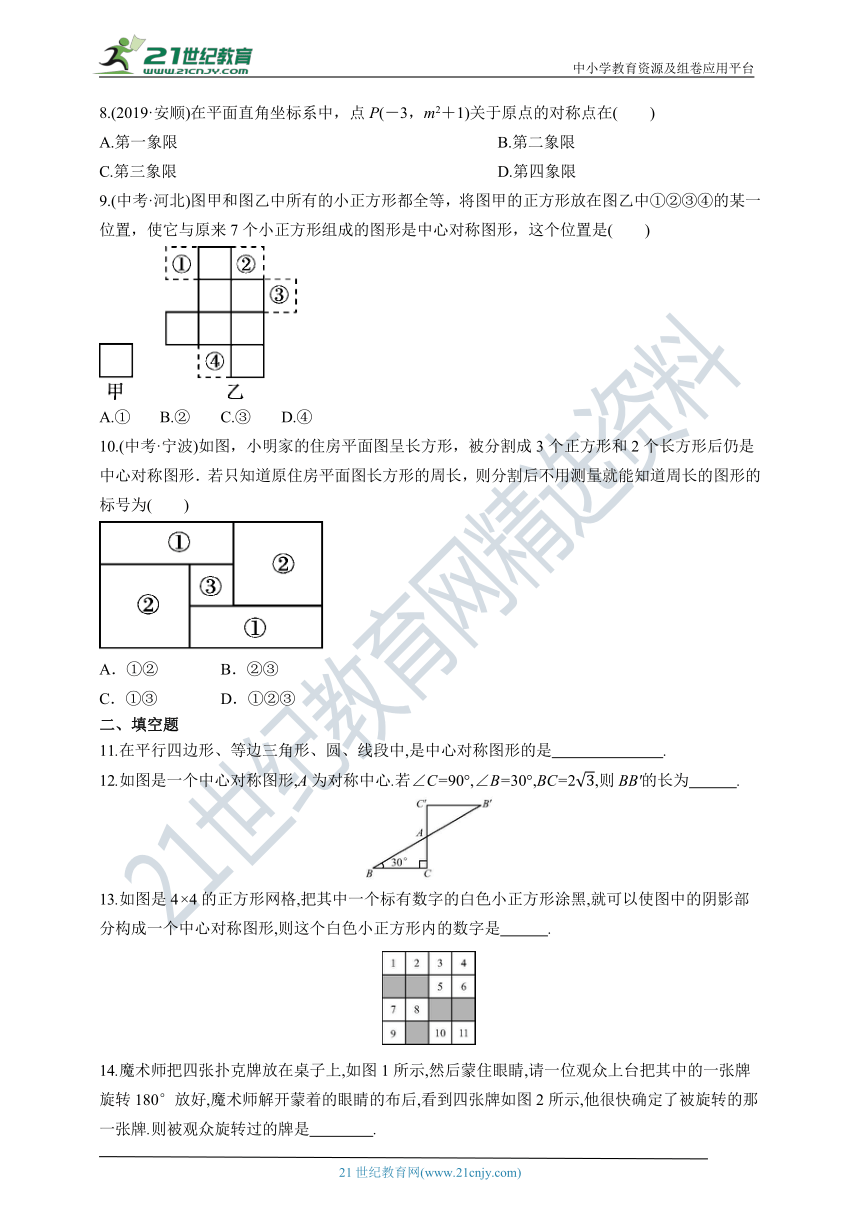
8.(2019·安顺)在平面直角坐标系中,点P(-3,m2+1)关于原点的对称点在( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
9.(中考·河北)图甲和图乙中所有的小正方形都全等,将图甲的正方形放在图乙中①②③④的某一位置,使它与原来7个小正方形组成的图形是中心对称图形,这个位置是( )
A.① B.② C.③ D.④
10.(中考·宁波)如图,小明家的住房平面图呈长方形,被分割成3个正方形和2个长方形后仍是中心对称图形.若只知道原住房平面图长方形的周长,则分割后不用测量就能知道周长的图形的标号为( )
A.①② B.②③
C.①③ D.①②③
二、填空题
11.在平行四边形、等边三角形、圆、线段中,是中心对称图形的是 .?
12.如图是一个中心对称图形,A为对称中心.若∠C=90°,∠B=30°,BC=23,则BB'的长为 .?
13.如图是4×4的正方形网格,把其中一个标有数字的白色小正方形涂黑,就可以使图中的阴影部分构成一个中心对称图形,则这个白色小正方形内的数字是 .?
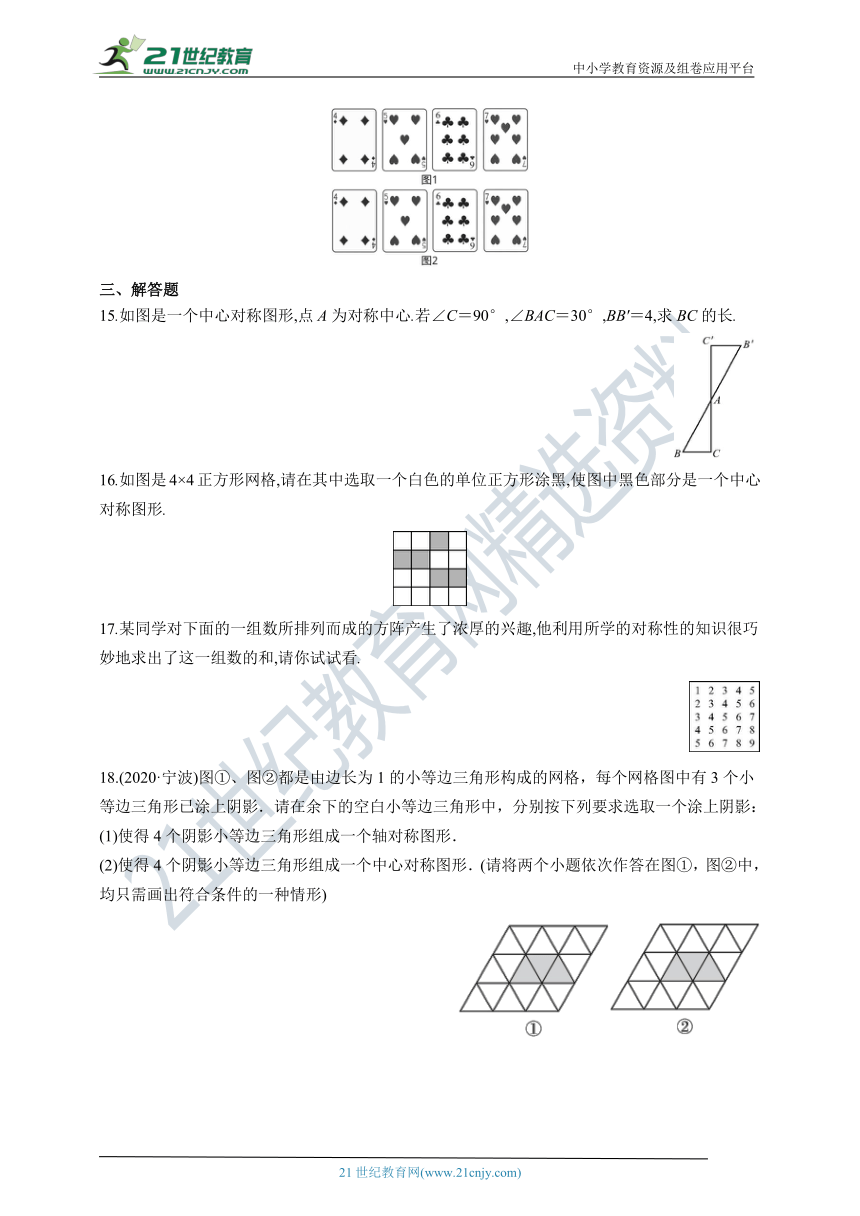
14.魔术师把四张扑克牌放在桌子上,如图1所示,然后蒙住眼睛,请一位观众上台把其中的一张牌旋转180°放好,魔术师解开蒙着的眼睛的布后,看到四张牌如图2所示,他很快确定了被旋转的那一张牌.则被观众旋转过的牌是 .?
三、解答题
15.如图是一个中心对称图形,点A为对称中心.若∠C=90°,∠BAC=30°,BB'=4,求BC的长.
16.如图是4×4正方形网格,请在其中选取一个白色的单位正方形涂黑,使图中黑色部分是一个中心对称图形.
17.某同学对下面的一组数所排列而成的方阵产生了浓厚的兴趣,他利用所学的对称性的知识很巧妙地求出了这一组数的和,请你试试看.
18.(2020·宁波)图①、图②都是由边长为1的小等边三角形构成的网格,每个网格图中有3个小等边三角形已涂上阴影.请在余下的空白小等边三角形中,分别按下列要求选取一个涂上阴影:
(1)使得4个阴影小等边三角形组成一个轴对称图形.
(2)使得4个阴影小等边三角形组成一个中心对称图形.(请将两个小题依次作答在图①,图②中,均只需画出符合条件的一种情形)
19.如图,在平面直角坐标系中,△ABC的三个顶点的坐标分别是A(-3,2),B(0,4),C(0,2).
(1)将△ABC以点C为旋转中心旋转180°,画出旋转后对应的△A1B1C;平移△ABC,若点A的对应点A2的坐标为(0,-4),画出平移后对应的△A2B2C2.
(2)若将△A1B1C绕某一点旋转可以得到△A2B2C2,请直接写出旋转中心的坐标.
(3)在x轴上有一点P,使得PA+PB的值最小,请直接写出点P的坐标.
20.如图,线段AC,BD相交于点O,且AB∥CD,AB=CD,此图形是中心对称图形吗?试说明你的理由.
21.如图,点O是平行四边形ABCD的对称中心,将直线BD绕点O顺时针方向旋转,分别交CD,AB于点E,F.
(1)证明:△DEO≌△BFO;
(2)若BD=2,AD=1,AB=5,当BD绕点O顺时针方向旋转45°时,判断四边形AECF的形状,并说明理由.
22.如图,在△ABC中,D是BC上一点,DE∥AC交AB于点E,DF∥AB交AC于点F.
(1)求证:四边形AEDF是中心对称图形;
(2)若AD平分∠BAC,求证:点E,F关于直线AD对称.
23.知识背景:过中心对称图形的对称中心的任意一条直线都将其分成全等的两个部分.
(1)如图1,直线m经过平行四边形ABCD对角线的交点O,则S四边形AEFB S四边形CFED;(填“>”“<”或“=”)?
(2)如图2,两个正方形如图所示摆放,O为小正方形对角线的交点,作过点O的直线将整个图形分成面积相等的两部分;
(3)八个大小相同的正方形如图3所示摆放,作直线将整个图形分成面积相等的两部分.(用三种方法分割)
参考答案
一、选择题
1.下列图形是我国国产品牌汽车的标识,这些汽车标识中,是中心对称图形的是 (D)
2.下列手机手势解锁图案中,是中心对称图形的是 (B)
3.下列图形中,既是轴对称图形,又是中心对称图形的是 (A)
4.(2020·遂宁)下列图形中,既是轴对称图形,又是中心对称图形的是( C )
A.等边三角形 B.平行四边形 C.矩形 D.正五边形
5.如图,该图形是中心对称图形,则对称中心是 (D)
A.点C B.点D C.线段BC的中点 D.线段FC的中点
6.如图,△ABC是一个中心对称图形的一部分,点O是对称中心,A和B是对应点,∠C=90°,那么将这个图形补充完整后是 (A)
A.矩形 B.菱形 C.正方形 D.梯形
7.(中考·宜昌)如图,若要添加一条线段,使之既是轴对称图形又是中心对称图形,正确的添加位置是( A )
8.(2019·安顺)在平面直角坐标系中,点P(-3,m2+1)关于原点的对称点在( D )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
9.(中考·河北)图甲和图乙中所有的小正方形都全等,将图甲的正方形放在图乙中①②③④的某一位置,使它与原来7个小正方形组成的图形是中心对称图形,这个位置是( C )
A.① B.② C.③ D.④
10.(中考·宁波)如图,小明家的住房平面图呈长方形,被分割成3个正方形和2个长方形后仍是中心对称图形.若只知道原住房平面图长方形的周长,则分割后不用测量就能知道周长的图形的标号为( )
A.①② B.②③
C.①③ D.①②③
【点拨】由题意知标①的两个长方形全等,标②的两个正方形全等.设长方形①的长为a,宽为c,正方形②的边长为b,正方形③的边长为d,则a+b=2b+d,即a=b+d;
b+c=2c+d,即c=b-d,于是有a+c=2b.
又因为大长方形的周长已知,不妨设为l,
所以2(a+b+b+c)=l,即8b=l,b=.
于是2(a+c)=4b=,故图形①②的周长可以确定.
【答案】A
二、填空题
11.在平行四边形、等边三角形、圆、线段中,是中心对称图形的是 平行四边形,圆,线段 .?
12.如图是一个中心对称图形,A为对称中心.若∠C=90°,∠B=30°,BC=23,则BB'的长为 8 .?
13.如图是4×4的正方形网格,把其中一个标有数字的白色小正方形涂黑,就可以使图中的阴影部分构成一个中心对称图形,则这个白色小正方形内的数字是 3 .?
14.魔术师把四张扑克牌放在桌子上,如图1所示,然后蒙住眼睛,请一位观众上台把其中的一张牌旋转180°放好,魔术师解开蒙着的眼睛的布后,看到四张牌如图2所示,他很快确定了被旋转的那一张牌.则被观众旋转过的牌是 方块4 .?
三、解答题
15.如图是一个中心对称图形,点A为对称中心.若∠C=90°,∠BAC=30°,BB'=4,求BC的长.
解:BC=1.
16.如图是4×4正方形网格,请在其中选取一个白色的单位正方形涂黑,使图中黑色部分是一个中心对称图形.
解:如图是一个中心对称图形.
17.某同学对下面的一组数所排列而成的方阵产生了浓厚的兴趣,他利用所学的对称性的知识很巧妙地求出了这一组数的和,请你试试看.
解:∵(1+9)+(2+8)+(3+7)+(4+6)+…+(8+2)+(3+7)+(4+6)+(5+5)+(6+4)+5=10×12+5=120+5=125,∴这组数的和为125.
18.(2020·宁波)图①、图②都是由边长为1的小等边三角形构成的网格,每个网格图中有3个小等边三角形已涂上阴影.请在余下的空白小等边三角形中,分别按下列要求选取一个涂上阴影:
(1)使得4个阴影小等边三角形组成一个轴对称图形.
解:轴对称图形如图①所示.(答案不唯一)
(2)使得4个阴影小等边三角形组成一个中心对称图形.(请将两个小题依次作答在图①,图②中,均只需画出符合条件的一种情形)
解:中心对称图形如图②所示.(答案不唯一)
19.如图,在平面直角坐标系中,△ABC的三个顶点的坐标分别是A(-3,2),B(0,4),C(0,2).
(1)将△ABC以点C为旋转中心旋转180°,画出旋转后对应的△A1B1C;平移△ABC,若点A的对应点A2的坐标为(0,-4),画出平移后对应的△A2B2C2.
【思路点拨】分别利用旋转、平移的性质作图即可;
解:如图所示.
(2)若将△A1B1C绕某一点旋转可以得到△A2B2C2,请直接写出旋转中心的坐标.
【思路点拨】先确定旋转角度为180°,再利用成中心对称的两个图形的性质找旋转中心;
解:旋转中心的坐标为.
(3)在x轴上有一点P,使得PA+PB的值最小,请直接写出点P的坐标.
【思路点拨】利用轴对称的性质作图,即可找到点P.
解:点P的坐标为(-2,0).
20.如图,线段AC,BD相交于点O,且AB∥CD,AB=CD,此图形是中心对称图形吗?试说明你的理由.
解:是中心对称图形,
∵AB∥CD,∴∠A=∠C,∠B=∠D.
在△AOB与△COD中,∠A=∠C,AB=CD,∠B=∠D,
∴△AOB≌△COD(ASA),
∴OA=OC,OB=OD,
∴此图形是中心对称图形.
21.如图,点O是平行四边形ABCD的对称中心,将直线BD绕点O顺时针方向旋转,分别交CD,AB于点E,F.
(1)证明:△DEO≌△BFO;
(2)若BD=2,AD=1,AB=5,当BD绕点O顺时针方向旋转45°时,判断四边形AECF的形状,并说明理由.
解:(1)在平行四边形ABCD中,CD∥AB,
∴∠CDO=∠ABO,∠DEO=∠BFO.
又∵点O是平行四边形ABCD的对称中心,
∴OD=OB,∴△DEO≌△BFO(AAS).
(2)四边形AECF是菱形,理由:∵在△ABD中,BD=2,AD=1,AB=5,∴BD2+AD2=AB2,
∴△ABD是直角三角形,且∠ADB=90°.
∵OD=OB=12BD=1,∴AD=OD,
∴△OAD是等腰直角三角形,
∴∠AOD=45°.当直线BD绕点O顺时针旋转45°时,即∠DOE=45°,∴∠AOE=90°.
∵△DEO≌△BFO,∴OE=OF,
又∵点O是平行四边形ABCD的对称中心,
∴OA=OC,
∴四边形AECF是菱形.
22.如图,在△ABC中,D是BC上一点,DE∥AC交AB于点E,DF∥AB交AC于点F.
(1)求证:四边形AEDF是中心对称图形;
(2)若AD平分∠BAC,求证:点E,F关于直线AD对称.
证明:(1)∵DE∥AC,DF∥AB,
∴四边形AEDF是平行四边形,
∴四边形AEDF是中心对称图形.
(2)连接EF.∵AD平分∠BAC,
∴∠BAD=∠CAD.
又∵DE∥AC,∴∠CAD=∠ADE,
∴∠BAD=∠ADE,
∴AE=DE.
由(1)知四边形AEDF是平行四边形,
∴四边形AEDF是菱形,∴AD垂直平分EF,
∴点E,F关于直线AD对称.
23.知识背景:过中心对称图形的对称中心的任意一条直线都将其分成全等的两个部分.
(1)如图1,直线m经过平行四边形ABCD对角线的交点O,则S四边形AEFB = S四边形CFED;(填“>”“<”或“=”)?
(2)如图2,两个正方形如图所示摆放,O为小正方形对角线的交点,作过点O的直线将整个图形分成面积相等的两部分;
(3)八个大小相同的正方形如图3所示摆放,作直线将整个图形分成面积相等的两部分.(用三种方法分割)
解:(2)如图1所示.
(3)如图2所示.(答案不唯一,合理即可)
23.2.2 中心对称图形
一、选择题
1.下列图形是我国国产品牌汽车的标识,这些汽车标识中,是中心对称图形的是 ( )
2.下列手机手势解锁图案中,是中心对称图形的是 ( )
3.下列图形中,既是轴对称图形,又是中心对称图形的是 ( )
4.(2020·遂宁)下列图形中,既是轴对称图形,又是中心对称图形的是( )
A.等边三角形 B.平行四边形 C.矩形 D.正五边形
5.如图,该图形是中心对称图形,则对称中心是 ( )
A.点C B.点D C.线段BC的中点 D.线段FC的中点
6.如图,△ABC是一个中心对称图形的一部分,点O是对称中心,A和B是对应点,∠C=90°,那么将这个图形补充完整后是 ( )
A.矩形 B.菱形 C.正方形 D.梯形
7.(中考·宜昌)如图,若要添加一条线段,使之既是轴对称图形又是中心对称图形,正确的添加位置是( )
8.(2019·安顺)在平面直角坐标系中,点P(-3,m2+1)关于原点的对称点在( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
9.(中考·河北)图甲和图乙中所有的小正方形都全等,将图甲的正方形放在图乙中①②③④的某一位置,使它与原来7个小正方形组成的图形是中心对称图形,这个位置是( )
A.① B.② C.③ D.④
10.(中考·宁波)如图,小明家的住房平面图呈长方形,被分割成3个正方形和2个长方形后仍是中心对称图形.若只知道原住房平面图长方形的周长,则分割后不用测量就能知道周长的图形的标号为( )
A.①② B.②③
C.①③ D.①②③
二、填空题
11.在平行四边形、等边三角形、圆、线段中,是中心对称图形的是 .?
12.如图是一个中心对称图形,A为对称中心.若∠C=90°,∠B=30°,BC=23,则BB'的长为 .?
13.如图是4×4的正方形网格,把其中一个标有数字的白色小正方形涂黑,就可以使图中的阴影部分构成一个中心对称图形,则这个白色小正方形内的数字是 .?
14.魔术师把四张扑克牌放在桌子上,如图1所示,然后蒙住眼睛,请一位观众上台把其中的一张牌旋转180°放好,魔术师解开蒙着的眼睛的布后,看到四张牌如图2所示,他很快确定了被旋转的那一张牌.则被观众旋转过的牌是 .?
三、解答题
15.如图是一个中心对称图形,点A为对称中心.若∠C=90°,∠BAC=30°,BB'=4,求BC的长.
16.如图是4×4正方形网格,请在其中选取一个白色的单位正方形涂黑,使图中黑色部分是一个中心对称图形.
17.某同学对下面的一组数所排列而成的方阵产生了浓厚的兴趣,他利用所学的对称性的知识很巧妙地求出了这一组数的和,请你试试看.
18.(2020·宁波)图①、图②都是由边长为1的小等边三角形构成的网格,每个网格图中有3个小等边三角形已涂上阴影.请在余下的空白小等边三角形中,分别按下列要求选取一个涂上阴影:
(1)使得4个阴影小等边三角形组成一个轴对称图形.
(2)使得4个阴影小等边三角形组成一个中心对称图形.(请将两个小题依次作答在图①,图②中,均只需画出符合条件的一种情形)
19.如图,在平面直角坐标系中,△ABC的三个顶点的坐标分别是A(-3,2),B(0,4),C(0,2).
(1)将△ABC以点C为旋转中心旋转180°,画出旋转后对应的△A1B1C;平移△ABC,若点A的对应点A2的坐标为(0,-4),画出平移后对应的△A2B2C2.
(2)若将△A1B1C绕某一点旋转可以得到△A2B2C2,请直接写出旋转中心的坐标.
(3)在x轴上有一点P,使得PA+PB的值最小,请直接写出点P的坐标.
20.如图,线段AC,BD相交于点O,且AB∥CD,AB=CD,此图形是中心对称图形吗?试说明你的理由.
21.如图,点O是平行四边形ABCD的对称中心,将直线BD绕点O顺时针方向旋转,分别交CD,AB于点E,F.
(1)证明:△DEO≌△BFO;
(2)若BD=2,AD=1,AB=5,当BD绕点O顺时针方向旋转45°时,判断四边形AECF的形状,并说明理由.
22.如图,在△ABC中,D是BC上一点,DE∥AC交AB于点E,DF∥AB交AC于点F.
(1)求证:四边形AEDF是中心对称图形;
(2)若AD平分∠BAC,求证:点E,F关于直线AD对称.
23.知识背景:过中心对称图形的对称中心的任意一条直线都将其分成全等的两个部分.
(1)如图1,直线m经过平行四边形ABCD对角线的交点O,则S四边形AEFB S四边形CFED;(填“>”“<”或“=”)?
(2)如图2,两个正方形如图所示摆放,O为小正方形对角线的交点,作过点O的直线将整个图形分成面积相等的两部分;
(3)八个大小相同的正方形如图3所示摆放,作直线将整个图形分成面积相等的两部分.(用三种方法分割)
参考答案
一、选择题
1.下列图形是我国国产品牌汽车的标识,这些汽车标识中,是中心对称图形的是 (D)
2.下列手机手势解锁图案中,是中心对称图形的是 (B)
3.下列图形中,既是轴对称图形,又是中心对称图形的是 (A)
4.(2020·遂宁)下列图形中,既是轴对称图形,又是中心对称图形的是( C )
A.等边三角形 B.平行四边形 C.矩形 D.正五边形
5.如图,该图形是中心对称图形,则对称中心是 (D)
A.点C B.点D C.线段BC的中点 D.线段FC的中点
6.如图,△ABC是一个中心对称图形的一部分,点O是对称中心,A和B是对应点,∠C=90°,那么将这个图形补充完整后是 (A)
A.矩形 B.菱形 C.正方形 D.梯形
7.(中考·宜昌)如图,若要添加一条线段,使之既是轴对称图形又是中心对称图形,正确的添加位置是( A )
8.(2019·安顺)在平面直角坐标系中,点P(-3,m2+1)关于原点的对称点在( D )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
9.(中考·河北)图甲和图乙中所有的小正方形都全等,将图甲的正方形放在图乙中①②③④的某一位置,使它与原来7个小正方形组成的图形是中心对称图形,这个位置是( C )
A.① B.② C.③ D.④
10.(中考·宁波)如图,小明家的住房平面图呈长方形,被分割成3个正方形和2个长方形后仍是中心对称图形.若只知道原住房平面图长方形的周长,则分割后不用测量就能知道周长的图形的标号为( )
A.①② B.②③
C.①③ D.①②③
【点拨】由题意知标①的两个长方形全等,标②的两个正方形全等.设长方形①的长为a,宽为c,正方形②的边长为b,正方形③的边长为d,则a+b=2b+d,即a=b+d;
b+c=2c+d,即c=b-d,于是有a+c=2b.
又因为大长方形的周长已知,不妨设为l,
所以2(a+b+b+c)=l,即8b=l,b=.
于是2(a+c)=4b=,故图形①②的周长可以确定.
【答案】A
二、填空题
11.在平行四边形、等边三角形、圆、线段中,是中心对称图形的是 平行四边形,圆,线段 .?
12.如图是一个中心对称图形,A为对称中心.若∠C=90°,∠B=30°,BC=23,则BB'的长为 8 .?
13.如图是4×4的正方形网格,把其中一个标有数字的白色小正方形涂黑,就可以使图中的阴影部分构成一个中心对称图形,则这个白色小正方形内的数字是 3 .?
14.魔术师把四张扑克牌放在桌子上,如图1所示,然后蒙住眼睛,请一位观众上台把其中的一张牌旋转180°放好,魔术师解开蒙着的眼睛的布后,看到四张牌如图2所示,他很快确定了被旋转的那一张牌.则被观众旋转过的牌是 方块4 .?
三、解答题
15.如图是一个中心对称图形,点A为对称中心.若∠C=90°,∠BAC=30°,BB'=4,求BC的长.
解:BC=1.
16.如图是4×4正方形网格,请在其中选取一个白色的单位正方形涂黑,使图中黑色部分是一个中心对称图形.
解:如图是一个中心对称图形.
17.某同学对下面的一组数所排列而成的方阵产生了浓厚的兴趣,他利用所学的对称性的知识很巧妙地求出了这一组数的和,请你试试看.
解:∵(1+9)+(2+8)+(3+7)+(4+6)+…+(8+2)+(3+7)+(4+6)+(5+5)+(6+4)+5=10×12+5=120+5=125,∴这组数的和为125.
18.(2020·宁波)图①、图②都是由边长为1的小等边三角形构成的网格,每个网格图中有3个小等边三角形已涂上阴影.请在余下的空白小等边三角形中,分别按下列要求选取一个涂上阴影:
(1)使得4个阴影小等边三角形组成一个轴对称图形.
解:轴对称图形如图①所示.(答案不唯一)
(2)使得4个阴影小等边三角形组成一个中心对称图形.(请将两个小题依次作答在图①,图②中,均只需画出符合条件的一种情形)
解:中心对称图形如图②所示.(答案不唯一)
19.如图,在平面直角坐标系中,△ABC的三个顶点的坐标分别是A(-3,2),B(0,4),C(0,2).
(1)将△ABC以点C为旋转中心旋转180°,画出旋转后对应的△A1B1C;平移△ABC,若点A的对应点A2的坐标为(0,-4),画出平移后对应的△A2B2C2.
【思路点拨】分别利用旋转、平移的性质作图即可;
解:如图所示.
(2)若将△A1B1C绕某一点旋转可以得到△A2B2C2,请直接写出旋转中心的坐标.
【思路点拨】先确定旋转角度为180°,再利用成中心对称的两个图形的性质找旋转中心;
解:旋转中心的坐标为.
(3)在x轴上有一点P,使得PA+PB的值最小,请直接写出点P的坐标.
【思路点拨】利用轴对称的性质作图,即可找到点P.
解:点P的坐标为(-2,0).
20.如图,线段AC,BD相交于点O,且AB∥CD,AB=CD,此图形是中心对称图形吗?试说明你的理由.
解:是中心对称图形,
∵AB∥CD,∴∠A=∠C,∠B=∠D.
在△AOB与△COD中,∠A=∠C,AB=CD,∠B=∠D,
∴△AOB≌△COD(ASA),
∴OA=OC,OB=OD,
∴此图形是中心对称图形.
21.如图,点O是平行四边形ABCD的对称中心,将直线BD绕点O顺时针方向旋转,分别交CD,AB于点E,F.
(1)证明:△DEO≌△BFO;
(2)若BD=2,AD=1,AB=5,当BD绕点O顺时针方向旋转45°时,判断四边形AECF的形状,并说明理由.
解:(1)在平行四边形ABCD中,CD∥AB,
∴∠CDO=∠ABO,∠DEO=∠BFO.
又∵点O是平行四边形ABCD的对称中心,
∴OD=OB,∴△DEO≌△BFO(AAS).
(2)四边形AECF是菱形,理由:∵在△ABD中,BD=2,AD=1,AB=5,∴BD2+AD2=AB2,
∴△ABD是直角三角形,且∠ADB=90°.
∵OD=OB=12BD=1,∴AD=OD,
∴△OAD是等腰直角三角形,
∴∠AOD=45°.当直线BD绕点O顺时针旋转45°时,即∠DOE=45°,∴∠AOE=90°.
∵△DEO≌△BFO,∴OE=OF,
又∵点O是平行四边形ABCD的对称中心,
∴OA=OC,
∴四边形AECF是菱形.
22.如图,在△ABC中,D是BC上一点,DE∥AC交AB于点E,DF∥AB交AC于点F.
(1)求证:四边形AEDF是中心对称图形;
(2)若AD平分∠BAC,求证:点E,F关于直线AD对称.
证明:(1)∵DE∥AC,DF∥AB,
∴四边形AEDF是平行四边形,
∴四边形AEDF是中心对称图形.
(2)连接EF.∵AD平分∠BAC,
∴∠BAD=∠CAD.
又∵DE∥AC,∴∠CAD=∠ADE,
∴∠BAD=∠ADE,
∴AE=DE.
由(1)知四边形AEDF是平行四边形,
∴四边形AEDF是菱形,∴AD垂直平分EF,
∴点E,F关于直线AD对称.
23.知识背景:过中心对称图形的对称中心的任意一条直线都将其分成全等的两个部分.
(1)如图1,直线m经过平行四边形ABCD对角线的交点O,则S四边形AEFB = S四边形CFED;(填“>”“<”或“=”)?
(2)如图2,两个正方形如图所示摆放,O为小正方形对角线的交点,作过点O的直线将整个图形分成面积相等的两部分;
(3)八个大小相同的正方形如图3所示摆放,作直线将整个图形分成面积相等的两部分.(用三种方法分割)
解:(2)如图1所示.
(3)如图2所示.(答案不唯一,合理即可)
同课章节目录
