人教八下课件矩形的性质
图片预览


文档简介
(共23张PPT)
19.2特殊的平行四边形
外语学校
liudeguang
19.2.1 矩形
19.2 特殊的平行四边形
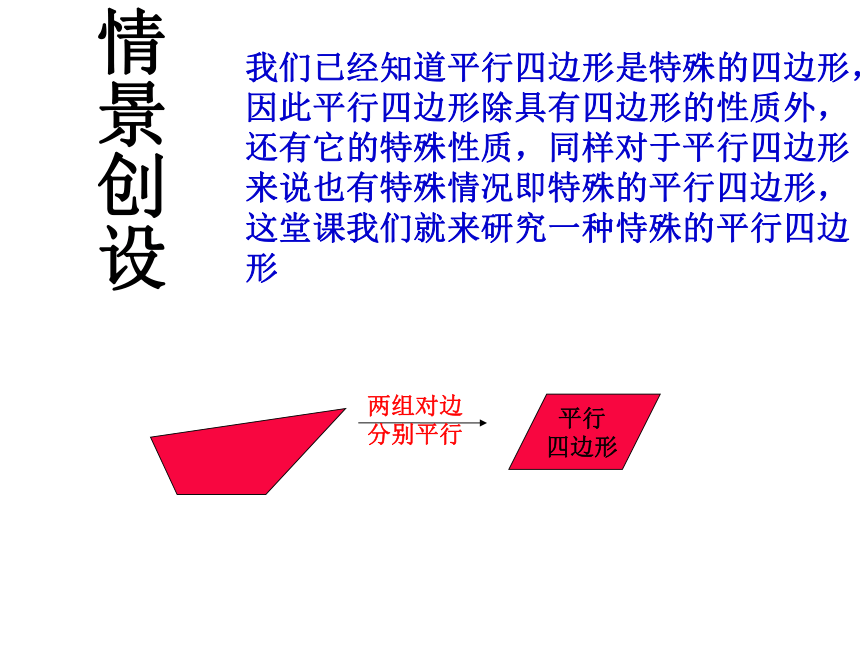
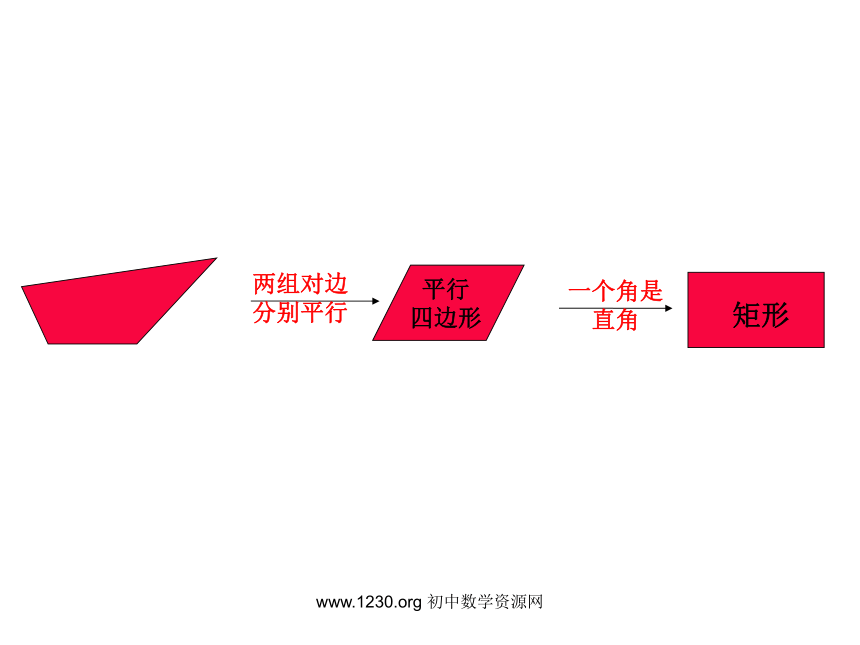
两组对边
分别平行
平行
四边形
情景创设
我们已经知道平行四边形是特殊的四边形,因此平行四边形除具有四边形的性质外,还有它的特殊性质,同样对于平行四边形来说也有特殊情况即特殊的平行四边形,这堂课我们就来研究一种恃殊的平行四边形
A
B
O
C
D
B
A
O
C
D
B
D
A
C
O
B
A
O
D
C
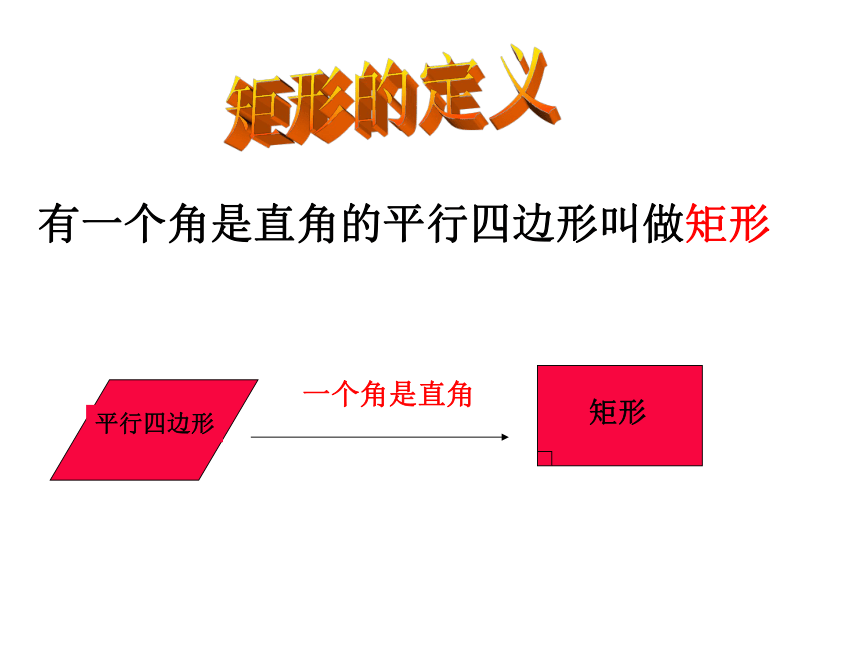
一个角是直角
有一个角是直角的平行四边形叫做矩形
矩形
平行四边形
两组对边
分别平行
一个角是
直角
平行
四边形
矩形
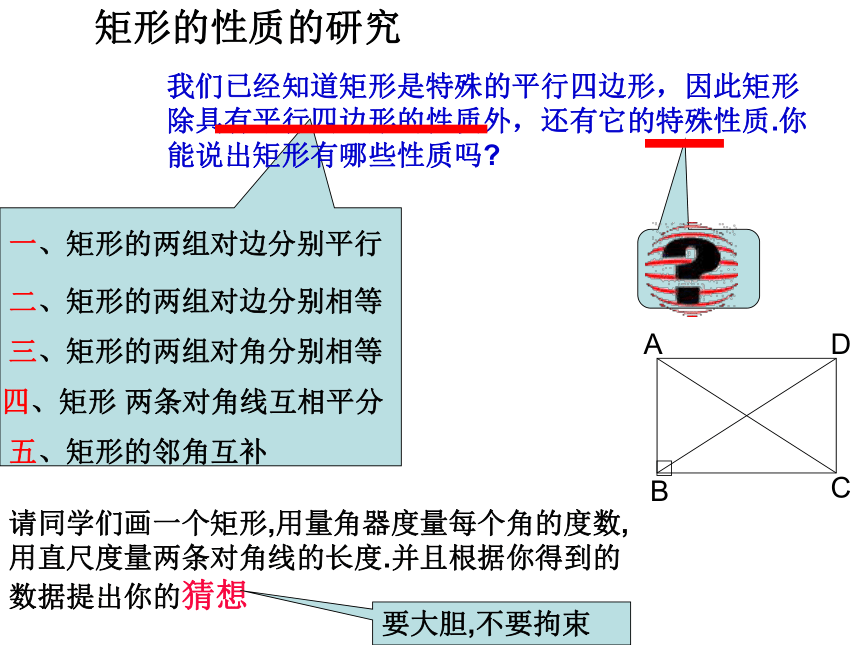
矩形的性质的研究
我们已经知道矩形是特殊的平行四边形,因此矩形除具有平行四边形的性质外,还有它的特殊性质.你能说出矩形有哪些性质吗
E 。
四、矩形 两条对角线互相平分
三、矩形的两组对角分别相等
二、矩形的两组对边分别相等
一、矩形的两组对边分别平行
五、矩形的邻角互补
请同学们画一个矩形,用量角器度量每个角的度数,用直尺度量两条对角线的长度.并且根据你得到的数据提出你的猜想
要大胆,不要拘束
A
B
C
D
□
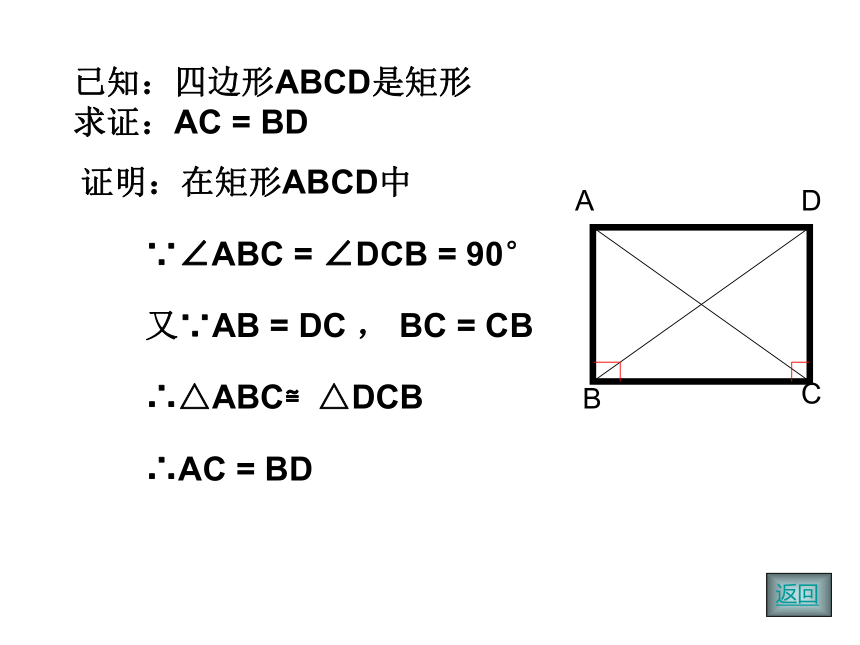
已知:四边形ABCD是矩形
求证:AC = BD
A
B
C
D
返回
证明:在矩形ABCD中
∵∠ABC = ∠DCB = 90°
又∵AB = DC , BC = CB
∴△ABC≌△DCB
∴AC = BD
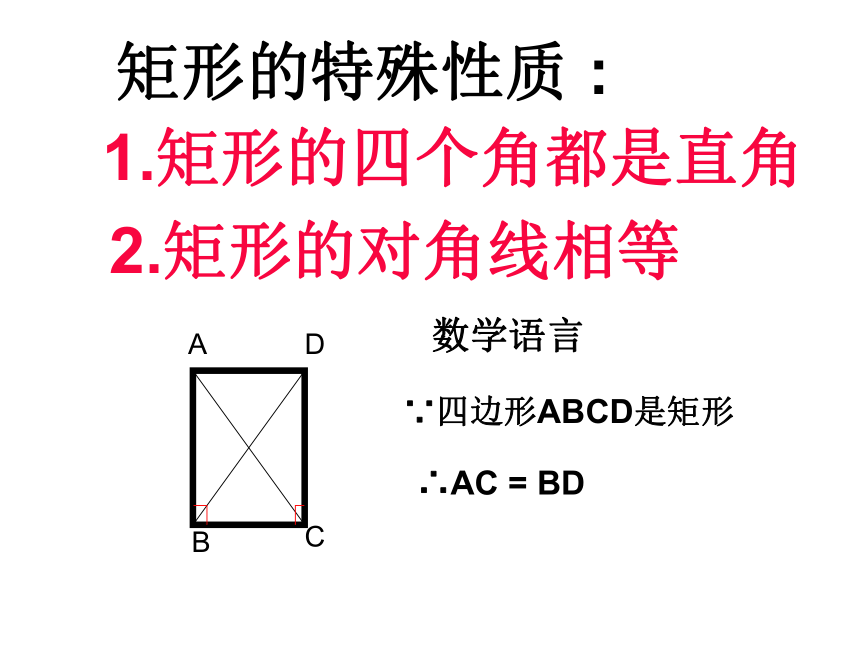
矩形的特殊性质 :
2.矩形的对角线相等
数学语言
A
B
C
D
∵四边形ABCD是矩形
∴AC = BD
1.矩形的四个角都是直角
矩形的 两条对角线互相平分
矩形的两组对边分别平行
矩形的两组对边分别相等
矩形的四个角都是直角
矩形 的两条对角线相等
边
对角线
角
数学语言
∵四边形ABCD是矩形
∴AD = BC ,CD = AB
∴AD ∥BC ,CD ∥AB
∴AC= BD
A
B
C
D
O
∴AO= CO ,OD = OB
推论:直角三角形斜边上的中线等
于斜边的一半.
如图,矩形ABCD中,对角线AC、BD相交于点O,请探讨OC与BD的关系
已知:在Rt△ABC中,∠ABC=900,BO是AC上的中线.
求证: BO = AC
O
C
B
A
D
D
证明: 延长BO至D,使OD=BO,
连结AD、DC.
∵AO=OC, BO=OD
∴四边形ABCD是平行四边形.
∵∠ABC=900
∴ ABCD是矩形
∴AC=BD
1
2
1
2
∴BO= BD= AC
再探新知
3.矩形是轴对称图形.
1.直角三角形斜边上的中线等于斜边的一半
再探新知
D
O
C
B
A
2.矩形的对角线把矩形分成两对全等的等腰三角形
有一个角是直角的
平行四边形叫矩形
2.矩形的性质:
对边平行且相等
四个角都是直角
对角线互相平分 且相等
1.矩形的定义:
边:
角:
对角线:
5.矩形是轴对称图形.
3.直角三角形斜边上的中线等于斜边的一半
4. 矩形的对角线把矩形分成两对全等的
等腰三角形
总结
例1 已知:矩形ABCD的两条对角线相交与O,∠AOD=120°,AB = 4cm.
求矩形对角线的长
∴BD = 2AB=2×4=8cm
A
B
C
D
O
1
解:∵四边形ABCD是矩形
∴OA = OD( )
∵ ∠AOD=120°
∴ ∠1=30°
又∵ ∠BAD=90°( )
矩形的对角线相等且平分
矩形的每个内角都是直角
例2:如图,矩形ABCD被两条对角线分成四个小三角形,如果四个小三角形的周长的和是86cm,对角线的长是13cm,那么矩形的周长是多少?
在矩形ABCD中,有
AD=BC;AB=CD;AC=DB;
AO=OC=OB=OD
∴AD+BC+AB+DC+2AC+2BD=86
又∵AC=DB=13
∴AD+AB+BC+DC=86-52=34
A
B
C
D
O
随堂练习
1. 矩形具有而一般平行四边形不具有的性质是( ).
A 对角线相等 B 对边相等
C 对角相等 D 对角线互相平分
A
2.在矩形ABCD中,
AE⊥BD于E,若
BE=OE=1,则
AC= , AB=---
B
C
D
E
A
O
4
2
3.如图,用8块相同的长方形地砖拼成一个矩形地面,则每块长方形地砖的长和宽分别是( )
(A)48cm,12cm; (B)48cm,16cm;
(C)44cm,16cm; (D)45cm,15cm.
60cm
D
(2).矩形的两条对角线将矩形分成四个面积
相等的等腰三角形( )
(1).矩形是平行四边形( )
4.矩形的短边长为3cm,两对角线所成的角是60 °,则它的另一边长是_______.
5. 已知矩形对角线长为4cm,一边长为 cm,
则矩形的面积是________.
cm2
6.判断题
(1)矩形具有而平行四边形不具有的性质( )
(A)内角和是360度(B)对角相等(C)对边平行且相等(D)对角线相等
(2)下面性质中,矩形不一定具有的是( )
(A)对角线相等(B)四个角相等(C)是轴对称图形(D)对角线垂直
(3)由已知矩形的一个顶点向其所对的对角线引垂线,该垂线分直角为3:1两部分,则垂线与另一条对角线的夹角是( )
(A)50度(B)45度(C)30度(D)22.5度
D
D
B
课堂练习
4. 过四边形的各个顶点分别作对角线的平行线,若这四
条平行线围成一个矩形,则原四边形一定是
课堂练习
A.对角线相等的四边形 B.对角线互相平分且相等的四边形
C.对角线互垂直平分的四边形 D.对角线垂直的四边形
5. 已知矩形的一条对角线与一边的夹角是40°,则两
条对角线所夹锐角的度数为
A.50° B.60° C.70° D.80°
6. 矩形ABCD中,AB=2BC,E在CD上,AE=AB,
则∠BAE等于
A.30° B.45° C.60° D.120°
[ ]
[ ]
[ ]
D
D
A
返回
如图,在矩形ABCD中,AC与BD相交于点O,AB=3cm,BC=4cm 则AC= cm,
AO= cm,BO= cm.
5
2.5
2.5
矩形的四个角都是直角.
※ 矩形的性质定理1
矩形的对角线相等.
※ 矩形的性质定理2
※ 推 论
直角三角形斜边上的中线等于斜边的一半.
矩形定义:
有一个角是直角的平行四边形叫做矩形.
19.2特殊的平行四边形
外语学校
liudeguang
19.2.1 矩形
19.2 特殊的平行四边形
两组对边
分别平行
平行
四边形
情景创设
我们已经知道平行四边形是特殊的四边形,因此平行四边形除具有四边形的性质外,还有它的特殊性质,同样对于平行四边形来说也有特殊情况即特殊的平行四边形,这堂课我们就来研究一种恃殊的平行四边形
A
B
O
C
D
B
A
O
C
D
B
D
A
C
O
B
A
O
D
C
一个角是直角
有一个角是直角的平行四边形叫做矩形
矩形
平行四边形
两组对边
分别平行
一个角是
直角
平行
四边形
矩形
矩形的性质的研究
我们已经知道矩形是特殊的平行四边形,因此矩形除具有平行四边形的性质外,还有它的特殊性质.你能说出矩形有哪些性质吗
E 。
四、矩形 两条对角线互相平分
三、矩形的两组对角分别相等
二、矩形的两组对边分别相等
一、矩形的两组对边分别平行
五、矩形的邻角互补
请同学们画一个矩形,用量角器度量每个角的度数,用直尺度量两条对角线的长度.并且根据你得到的数据提出你的猜想
要大胆,不要拘束
A
B
C
D
□
已知:四边形ABCD是矩形
求证:AC = BD
A
B
C
D
返回
证明:在矩形ABCD中
∵∠ABC = ∠DCB = 90°
又∵AB = DC , BC = CB
∴△ABC≌△DCB
∴AC = BD
矩形的特殊性质 :
2.矩形的对角线相等
数学语言
A
B
C
D
∵四边形ABCD是矩形
∴AC = BD
1.矩形的四个角都是直角
矩形的 两条对角线互相平分
矩形的两组对边分别平行
矩形的两组对边分别相等
矩形的四个角都是直角
矩形 的两条对角线相等
边
对角线
角
数学语言
∵四边形ABCD是矩形
∴AD = BC ,CD = AB
∴AD ∥BC ,CD ∥AB
∴AC= BD
A
B
C
D
O
∴AO= CO ,OD = OB
推论:直角三角形斜边上的中线等
于斜边的一半.
如图,矩形ABCD中,对角线AC、BD相交于点O,请探讨OC与BD的关系
已知:在Rt△ABC中,∠ABC=900,BO是AC上的中线.
求证: BO = AC
O
C
B
A
D
D
证明: 延长BO至D,使OD=BO,
连结AD、DC.
∵AO=OC, BO=OD
∴四边形ABCD是平行四边形.
∵∠ABC=900
∴ ABCD是矩形
∴AC=BD
1
2
1
2
∴BO= BD= AC
再探新知
3.矩形是轴对称图形.
1.直角三角形斜边上的中线等于斜边的一半
再探新知
D
O
C
B
A
2.矩形的对角线把矩形分成两对全等的等腰三角形
有一个角是直角的
平行四边形叫矩形
2.矩形的性质:
对边平行且相等
四个角都是直角
对角线互相平分 且相等
1.矩形的定义:
边:
角:
对角线:
5.矩形是轴对称图形.
3.直角三角形斜边上的中线等于斜边的一半
4. 矩形的对角线把矩形分成两对全等的
等腰三角形
总结
例1 已知:矩形ABCD的两条对角线相交与O,∠AOD=120°,AB = 4cm.
求矩形对角线的长
∴BD = 2AB=2×4=8cm
A
B
C
D
O
1
解:∵四边形ABCD是矩形
∴OA = OD( )
∵ ∠AOD=120°
∴ ∠1=30°
又∵ ∠BAD=90°( )
矩形的对角线相等且平分
矩形的每个内角都是直角
例2:如图,矩形ABCD被两条对角线分成四个小三角形,如果四个小三角形的周长的和是86cm,对角线的长是13cm,那么矩形的周长是多少?
在矩形ABCD中,有
AD=BC;AB=CD;AC=DB;
AO=OC=OB=OD
∴AD+BC+AB+DC+2AC+2BD=86
又∵AC=DB=13
∴AD+AB+BC+DC=86-52=34
A
B
C
D
O
随堂练习
1. 矩形具有而一般平行四边形不具有的性质是( ).
A 对角线相等 B 对边相等
C 对角相等 D 对角线互相平分
A
2.在矩形ABCD中,
AE⊥BD于E,若
BE=OE=1,则
AC= , AB=---
B
C
D
E
A
O
4
2
3.如图,用8块相同的长方形地砖拼成一个矩形地面,则每块长方形地砖的长和宽分别是( )
(A)48cm,12cm; (B)48cm,16cm;
(C)44cm,16cm; (D)45cm,15cm.
60cm
D
(2).矩形的两条对角线将矩形分成四个面积
相等的等腰三角形( )
(1).矩形是平行四边形( )
4.矩形的短边长为3cm,两对角线所成的角是60 °,则它的另一边长是_______.
5. 已知矩形对角线长为4cm,一边长为 cm,
则矩形的面积是________.
cm2
6.判断题
(1)矩形具有而平行四边形不具有的性质( )
(A)内角和是360度(B)对角相等(C)对边平行且相等(D)对角线相等
(2)下面性质中,矩形不一定具有的是( )
(A)对角线相等(B)四个角相等(C)是轴对称图形(D)对角线垂直
(3)由已知矩形的一个顶点向其所对的对角线引垂线,该垂线分直角为3:1两部分,则垂线与另一条对角线的夹角是( )
(A)50度(B)45度(C)30度(D)22.5度
D
D
B
课堂练习
4. 过四边形的各个顶点分别作对角线的平行线,若这四
条平行线围成一个矩形,则原四边形一定是
课堂练习
A.对角线相等的四边形 B.对角线互相平分且相等的四边形
C.对角线互垂直平分的四边形 D.对角线垂直的四边形
5. 已知矩形的一条对角线与一边的夹角是40°,则两
条对角线所夹锐角的度数为
A.50° B.60° C.70° D.80°
6. 矩形ABCD中,AB=2BC,E在CD上,AE=AB,
则∠BAE等于
A.30° B.45° C.60° D.120°
[ ]
[ ]
[ ]
D
D
A
返回
如图,在矩形ABCD中,AC与BD相交于点O,AB=3cm,BC=4cm 则AC= cm,
AO= cm,BO= cm.
5
2.5
2.5
矩形的四个角都是直角.
※ 矩形的性质定理1
矩形的对角线相等.
※ 矩形的性质定理2
※ 推 论
直角三角形斜边上的中线等于斜边的一半.
矩形定义:
有一个角是直角的平行四边形叫做矩形.
