动 态 几 何---面积的求法
图片预览

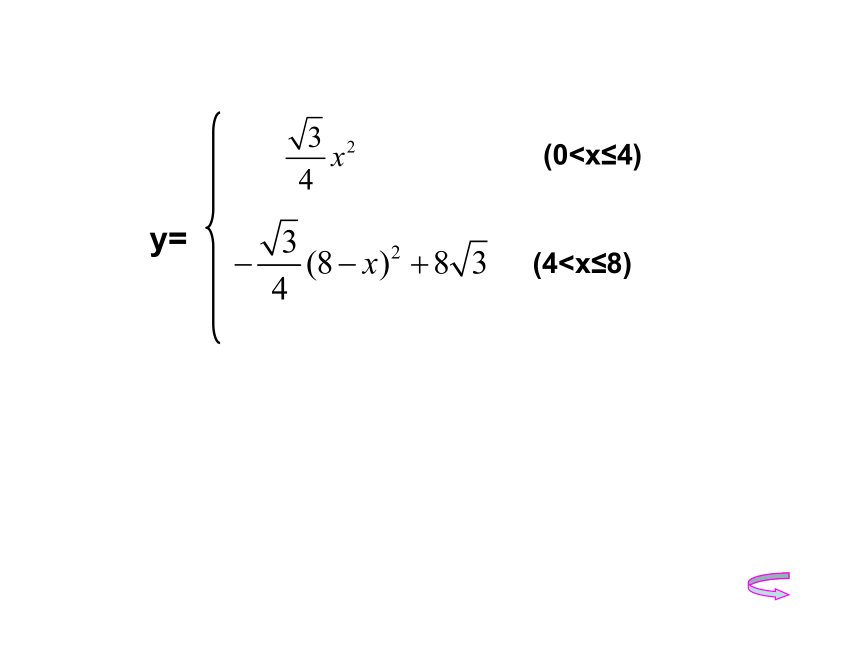

文档简介
(共25张PPT)
动 态 几 何
---面积的求法
一、点的运动变化引起面积的变化
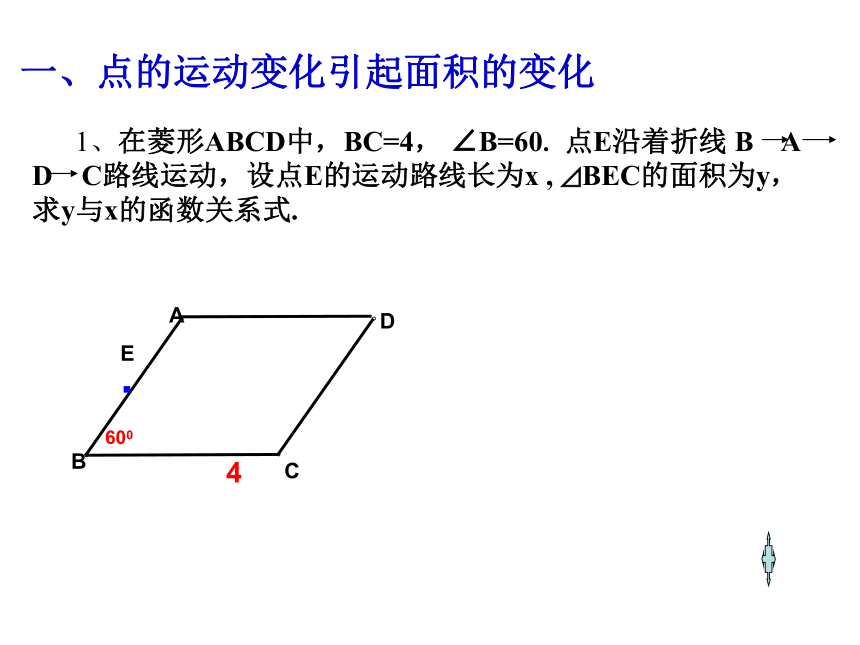
1、在菱形ABCD中,BC=4, ∠B=60. 点E沿着折线 B A D C路线运动,设点E的运动路线长为x , ⊿BEC的面积为y,求y与x的函数关系式.
4
600
D
A
C
B
·
E
一、点的运动变化引起面积的变化
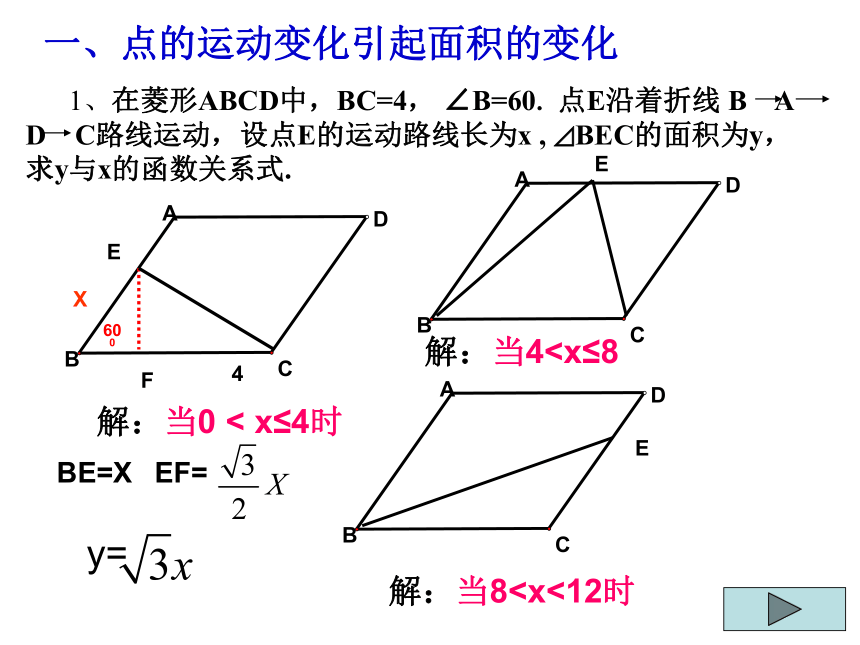
1、在菱形ABCD中,BC=4, ∠B=60. 点E沿着折线 B A D C路线运动,设点E的运动路线长为x , ⊿BEC的面积为y,求y与x的函数关系式.
4
600
·
D
A
C
B
E
X
F
D
A
C
B
E
D
A
C
B
E
解:当0 < x≤4时
y=
解:当4解:当8BE=X
EF=
一、点的运动变化引起面积的变化
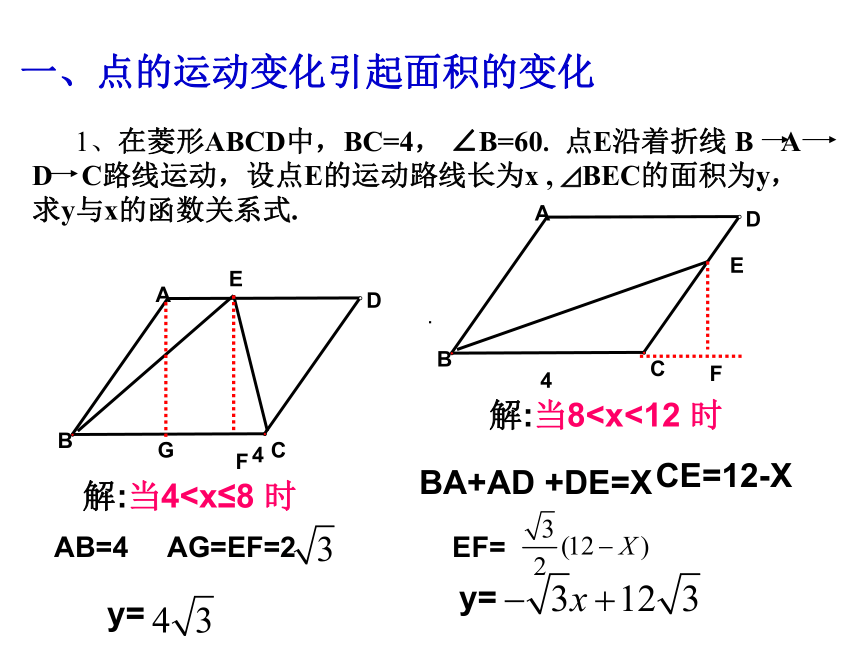
1、在菱形ABCD中,BC=4, ∠B=60. 点E沿着折线 B A D C路线运动,设点E的运动路线长为x , ⊿BEC的面积为y,求y与x的函数关系式.
4
·
D
A
C
B
E
解:当4D
A
C
B
E
解:当8F
F
4
y=
G
y=
AB=4
AG=EF=2
BA+AD +DE=X
CE=12-X
EF=
一、点的运动变化引起面积的变化
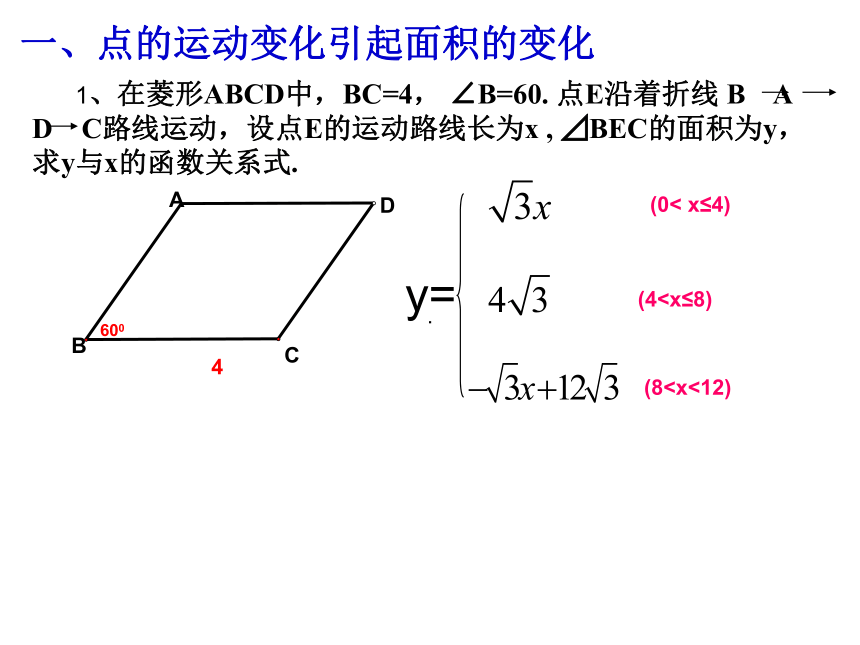
1、在菱形ABCD中,BC=4, ∠B=60. 点E沿着折线 B A D C路线运动,设点E的运动路线长为x , ⊿BEC的面积为y,求y与x的函数关系式.
4
600
·
D
A
C
B
(4(8(0< x≤4)
y=
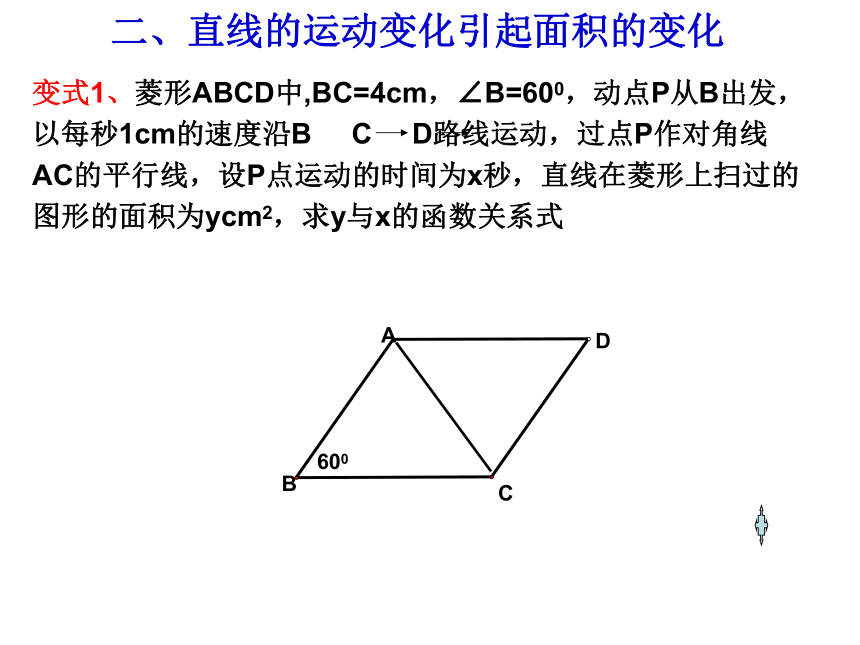
二、直线的运动变化引起面积的变化
变式1、菱形ABCD中,BC=4cm,∠B=600,动点P从B出发,以每秒1cm的速度沿B C D路线运动,过点P作对角线AC的平行线,设P点运动的时间为x秒,直线在菱形上扫过的图形的面积为ycm2,求y与x的函数关系式
D
A
C
B
600
二、直线的运动变化引起面积的变化
D
A
C
B
600
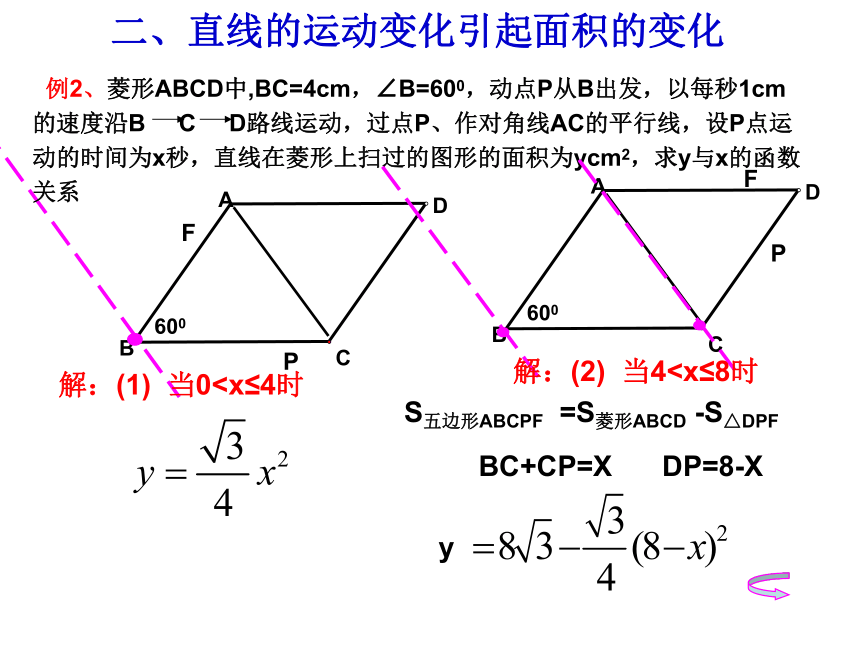
例2、菱形ABCD中,BC=4cm,∠B=600,动点P从B出发,以每秒1cm的速度沿B C D路线运动,过点P、作对角线AC的平行线,设P点运动的时间为x秒,直线在菱形上扫过的图形的面积为ycm2,求y与x的函数关系
P
F
D
A
C
B
600
P
F
解:(1) 当0解:(2) 当4BC+CP=X
DP=8-X
S五边形ABCPF =S菱形ABCD -S△DPF
y
y=
(0(4小结
动态几何的一般解题方法:
1、先分解图形的运动过程,寻找临界点;
2、然后画出图形动态变化草图,将复杂的运动问题转化为简单的数学问题;
3、找出图形动态变化中的常量和变量,抓住自变量的取值范围进行讨论,并求出它们之间的函数关系。
●数形结合、分类讨论是解决几何动态题的重要思想。
●求不规则图形面积时应采用转化的方法。
变式:菱形ABCD中,BC=4cm,∠B=600,动点P从B出发,以每秒1cm的速度沿B C D路线运动,点P出发2秒后,动点Q从B出发,在BC上以每秒1cm的速度运动,在CD上以每秒2cm的速度沿B C D运动,过P、Q两点分别作对角线AC的平行线,设P点运动的时间为x秒,这两条平行线在菱形上截出的图形的面积为ycm2,求面积y与时间x的关系式
D
B
C
A
P
C
D
A
B
P
E
解:(1)当0 < x≤2时
C
D
A
B
解:(2)当2<x≤4时
P
M
Q
N
C
D
A
B
P
Q
M
N
C
D
A
B
P
N
M
Q
解:(3)当4<x≤6时
解:(4)当6<x < 8时
例3:如图,已知直线 交坐标轴于 两点,以线段 为边向上作正方形 ,若正方形以每秒 个单位长度的速度沿射线 下滑,直至顶点 落在 轴上时停止.设正方形落在 轴下方部分的面积为 ,求 关于滑行时间 的函数关系式,并写出相应自变量 的取值范围;
三、图形的运动变化引起面积的变化
O
X
y
A
B
C
D
A
B
C
D
X
F
A
B
C
D
F
H
A
B
C
D
X
y
O
A’
B’
X
y
A’
B’
F
H
解:(1)当0<t≤1时
解:(2)当1<t≤2时
解:(3)当2<t≤3时
O
(2,0)
(2,0)
(0,1)
(0,1)
A’
y
(2,0)
(0,1)
O
B’
图1
解:应分三种情况考虑
图2
图3
动态几何问题
点动
线动
面动
清楚运
动规律
化动为静
策略
思想方法
小 结
类型
分类讨论
数形结合
转化思想
作业:练习纸
谢 谢 指 导 !
作业:Rt△PMN中,∠P=90°,PM=PN,MN=8cm,矩形ABCD的长和宽分别为8cm和2cm,C点和M点重合,BC和MN在一条直线上。令Rt△PMN不动,矩形ABCD沿MN所在直线向右以每秒1cm的速度移动,直到C点与N点重合为止。设移动x秒后,矩形ABCD与△PMN重叠部分的面积为y,
(1)求y与x之间的函数关系式?
(2)若重叠部分的面积为等腰直角ΔPMN面积的一半,求x?
A
B
C
D
M
N
P
8
2
8
热点聚焦 中考在线
8cm
8cm
2cm
(1) 0≤t≤2
(2) 2<t≤6
(3) 6<t≤8
F
A
B
C
D
M
N
P
8
2
8
A
B
C
D
2
8
解:(1)当0≤x≤2时,
∵MC=xcm,∠PMN=450
∴CE=xcm,
∴S重叠=SΔCEM= x2cm2
G
F
E
A
B
C
D
M
N
P
8
2
8
A
B
C
D
G
F
H
T
解:(2)当2<x≤6时,
∵MC=x,MF=GF=2,
∴CF=GD= x-2
∴S重叠=S梯形MCDG= (x-2+x) 2= 2x-2
A
B
C
D
M
N
P
8
A
B
C
D
G
F
H
T
解:(3)当6<x≤8时,
∴S重叠=S五边形GMCQH=S梯形GMNH-SΔQCN
Q
=12- (8-x)2
∵y=
x2 ,
0≤x≤2
2x-2,
2<x≤6
12- (8-x)2,
6<x≤8
(2)若重叠部分的面积为等腰直角ΔPMN面积的一半,求x?
则若 x2 =8,则x=±4,不合题意舍去
M
N
P
8
∵SΔPMN= ×4×8=16
则若2x-2 =8,则x=5,合题意,保留
∴当x=5时,重叠部分的面积为RtΔPNN的面积的一半
(2009衡阳)如图12,直线 与两坐标轴分别相交于A、B点,点M是线段AB上任意一点(A、B两点除外),过M分别作MC⊥OA于点C,MD⊥OB于D.
(1)当点M在AB上运动时,你认为四边形OCMD的周长是否发生变化?并说明理由;
(2)当点M运动到什么位置时,四边形OCMD的面积有最大值?最大值是多少?
(3)当四边形OCMD为正方形时,将四边形OCMD沿着x轴的正方向移动,设平移的距离为,正方形OCMD与△AOB重叠部分的面积为S.试求S与的函数关系式并画出该函数的图象.
三、图形的运动变化引起面积的变化
B
x
y
M
C
D
O
A
图12(1)
B
x
y
O
A
图12(2)
B
x
y
O
A
图12(3)
动 态 几 何
---面积的求法
一、点的运动变化引起面积的变化
1、在菱形ABCD中,BC=4, ∠B=60. 点E沿着折线 B A D C路线运动,设点E的运动路线长为x , ⊿BEC的面积为y,求y与x的函数关系式.
4
600
D
A
C
B
·
E
一、点的运动变化引起面积的变化
1、在菱形ABCD中,BC=4, ∠B=60. 点E沿着折线 B A D C路线运动,设点E的运动路线长为x , ⊿BEC的面积为y,求y与x的函数关系式.
4
600
·
D
A
C
B
E
X
F
D
A
C
B
E
D
A
C
B
E
解:当0 < x≤4时
y=
解:当4
EF=
一、点的运动变化引起面积的变化
1、在菱形ABCD中,BC=4, ∠B=60. 点E沿着折线 B A D C路线运动,设点E的运动路线长为x , ⊿BEC的面积为y,求y与x的函数关系式.
4
·
D
A
C
B
E
解:当4
A
C
B
E
解:当8
F
4
y=
G
y=
AB=4
AG=EF=2
BA+AD +DE=X
CE=12-X
EF=
一、点的运动变化引起面积的变化
1、在菱形ABCD中,BC=4, ∠B=60. 点E沿着折线 B A D C路线运动,设点E的运动路线长为x , ⊿BEC的面积为y,求y与x的函数关系式.
4
600
·
D
A
C
B
(4
y=
二、直线的运动变化引起面积的变化
变式1、菱形ABCD中,BC=4cm,∠B=600,动点P从B出发,以每秒1cm的速度沿B C D路线运动,过点P作对角线AC的平行线,设P点运动的时间为x秒,直线在菱形上扫过的图形的面积为ycm2,求y与x的函数关系式
D
A
C
B
600
二、直线的运动变化引起面积的变化
D
A
C
B
600
例2、菱形ABCD中,BC=4cm,∠B=600,动点P从B出发,以每秒1cm的速度沿B C D路线运动,过点P、作对角线AC的平行线,设P点运动的时间为x秒,直线在菱形上扫过的图形的面积为ycm2,求y与x的函数关系
P
F
D
A
C
B
600
P
F
解:(1) 当0
DP=8-X
S五边形ABCPF =S菱形ABCD -S△DPF
y
y=
(0
动态几何的一般解题方法:
1、先分解图形的运动过程,寻找临界点;
2、然后画出图形动态变化草图,将复杂的运动问题转化为简单的数学问题;
3、找出图形动态变化中的常量和变量,抓住自变量的取值范围进行讨论,并求出它们之间的函数关系。
●数形结合、分类讨论是解决几何动态题的重要思想。
●求不规则图形面积时应采用转化的方法。
变式:菱形ABCD中,BC=4cm,∠B=600,动点P从B出发,以每秒1cm的速度沿B C D路线运动,点P出发2秒后,动点Q从B出发,在BC上以每秒1cm的速度运动,在CD上以每秒2cm的速度沿B C D运动,过P、Q两点分别作对角线AC的平行线,设P点运动的时间为x秒,这两条平行线在菱形上截出的图形的面积为ycm2,求面积y与时间x的关系式
D
B
C
A
P
C
D
A
B
P
E
解:(1)当0 < x≤2时
C
D
A
B
解:(2)当2<x≤4时
P
M
Q
N
C
D
A
B
P
Q
M
N
C
D
A
B
P
N
M
Q
解:(3)当4<x≤6时
解:(4)当6<x < 8时
例3:如图,已知直线 交坐标轴于 两点,以线段 为边向上作正方形 ,若正方形以每秒 个单位长度的速度沿射线 下滑,直至顶点 落在 轴上时停止.设正方形落在 轴下方部分的面积为 ,求 关于滑行时间 的函数关系式,并写出相应自变量 的取值范围;
三、图形的运动变化引起面积的变化
O
X
y
A
B
C
D
A
B
C
D
X
F
A
B
C
D
F
H
A
B
C
D
X
y
O
A’
B’
X
y
A’
B’
F
H
解:(1)当0<t≤1时
解:(2)当1<t≤2时
解:(3)当2<t≤3时
O
(2,0)
(2,0)
(0,1)
(0,1)
A’
y
(2,0)
(0,1)
O
B’
图1
解:应分三种情况考虑
图2
图3
动态几何问题
点动
线动
面动
清楚运
动规律
化动为静
策略
思想方法
小 结
类型
分类讨论
数形结合
转化思想
作业:练习纸
谢 谢 指 导 !
作业:Rt△PMN中,∠P=90°,PM=PN,MN=8cm,矩形ABCD的长和宽分别为8cm和2cm,C点和M点重合,BC和MN在一条直线上。令Rt△PMN不动,矩形ABCD沿MN所在直线向右以每秒1cm的速度移动,直到C点与N点重合为止。设移动x秒后,矩形ABCD与△PMN重叠部分的面积为y,
(1)求y与x之间的函数关系式?
(2)若重叠部分的面积为等腰直角ΔPMN面积的一半,求x?
A
B
C
D
M
N
P
8
2
8
热点聚焦 中考在线
8cm
8cm
2cm
(1) 0≤t≤2
(2) 2<t≤6
(3) 6<t≤8
F
A
B
C
D
M
N
P
8
2
8
A
B
C
D
2
8
解:(1)当0≤x≤2时,
∵MC=xcm,∠PMN=450
∴CE=xcm,
∴S重叠=SΔCEM= x2cm2
G
F
E
A
B
C
D
M
N
P
8
2
8
A
B
C
D
G
F
H
T
解:(2)当2<x≤6时,
∵MC=x,MF=GF=2,
∴CF=GD= x-2
∴S重叠=S梯形MCDG= (x-2+x) 2= 2x-2
A
B
C
D
M
N
P
8
A
B
C
D
G
F
H
T
解:(3)当6<x≤8时,
∴S重叠=S五边形GMCQH=S梯形GMNH-SΔQCN
Q
=12- (8-x)2
∵y=
x2 ,
0≤x≤2
2x-2,
2<x≤6
12- (8-x)2,
6<x≤8
(2)若重叠部分的面积为等腰直角ΔPMN面积的一半,求x?
则若 x2 =8,则x=±4,不合题意舍去
M
N
P
8
∵SΔPMN= ×4×8=16
则若2x-2 =8,则x=5,合题意,保留
∴当x=5时,重叠部分的面积为RtΔPNN的面积的一半
(2009衡阳)如图12,直线 与两坐标轴分别相交于A、B点,点M是线段AB上任意一点(A、B两点除外),过M分别作MC⊥OA于点C,MD⊥OB于D.
(1)当点M在AB上运动时,你认为四边形OCMD的周长是否发生变化?并说明理由;
(2)当点M运动到什么位置时,四边形OCMD的面积有最大值?最大值是多少?
(3)当四边形OCMD为正方形时,将四边形OCMD沿着x轴的正方向移动,设平移的距离为,正方形OCMD与△AOB重叠部分的面积为S.试求S与的函数关系式并画出该函数的图象.
三、图形的运动变化引起面积的变化
B
x
y
M
C
D
O
A
图12(1)
B
x
y
O
A
图12(2)
B
x
y
O
A
图12(3)
同课章节目录
