查漏补缺,病理诊断方法指导,专题教学.ppt
文档属性
| 名称 | 查漏补缺,病理诊断方法指导,专题教学.ppt |

|
|
| 格式 | zip | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-05-15 00:00:00 | ||
图片预览



文档简介
(共47张PPT)
查漏补缺,病理诊断
方法指导,专题教学
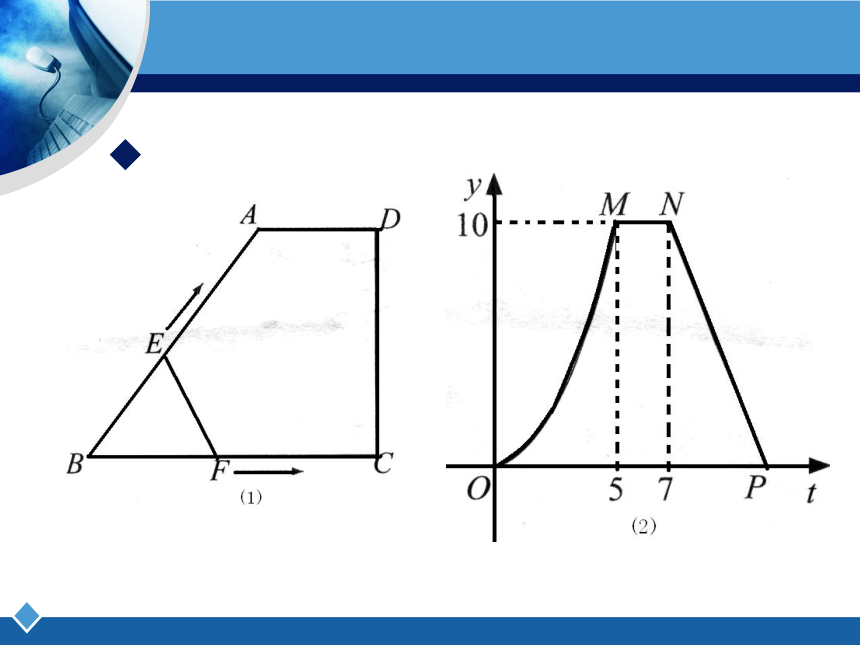
如图①,梯形ABCD中,∠C=90°.动点E、F同时从点B出发,点E沿折线 BA—AD—DC运动到点C时停止运动,点F沿BC运动到点C时停止运动,它们运动时的速度都是1 cm/s.设E、F出发t s时,△EBF的面积为y cm2.已知y与t的函数图象如图②所示,其中曲线OM为抛物线的一部分,MN、NP为线段.请根据图中的信息,解答下列问题:(1)梯形上底的长AD=_____cm,梯形ABCD的面积_____cm2;
(2)当点E在BA、DC上运动时,分别求出y与t的函数关系式(注明自变量的取值范围);
(3)当t为何值时,△EBF与梯形ABCD的面积之比为1:2.
题目
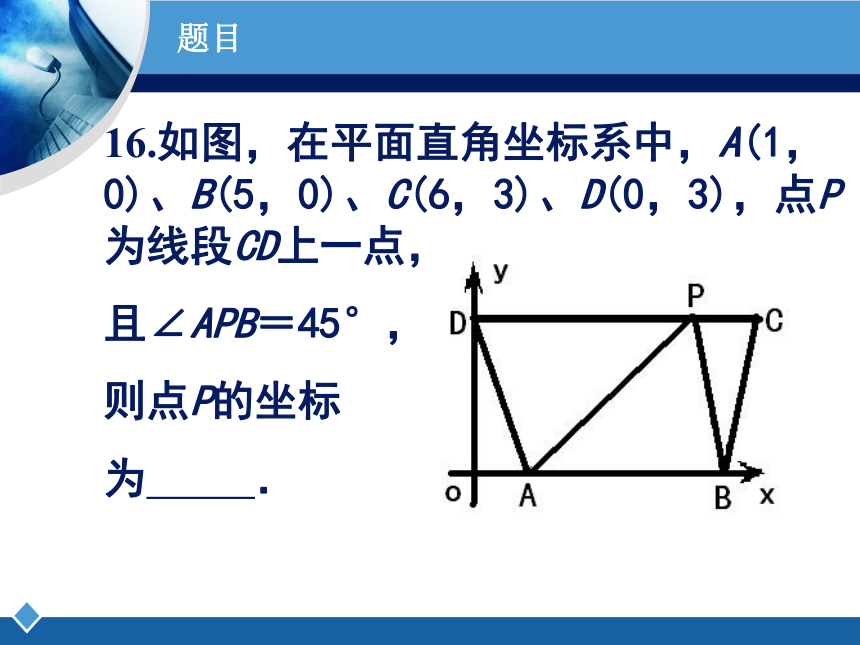
16.如图,在平面直角坐标系中,A(1,0)、B(5,0)、C(6,3)、D(0,3),点P为线段CD上一点,
且∠APB=45°,
则点P的坐标
为 .
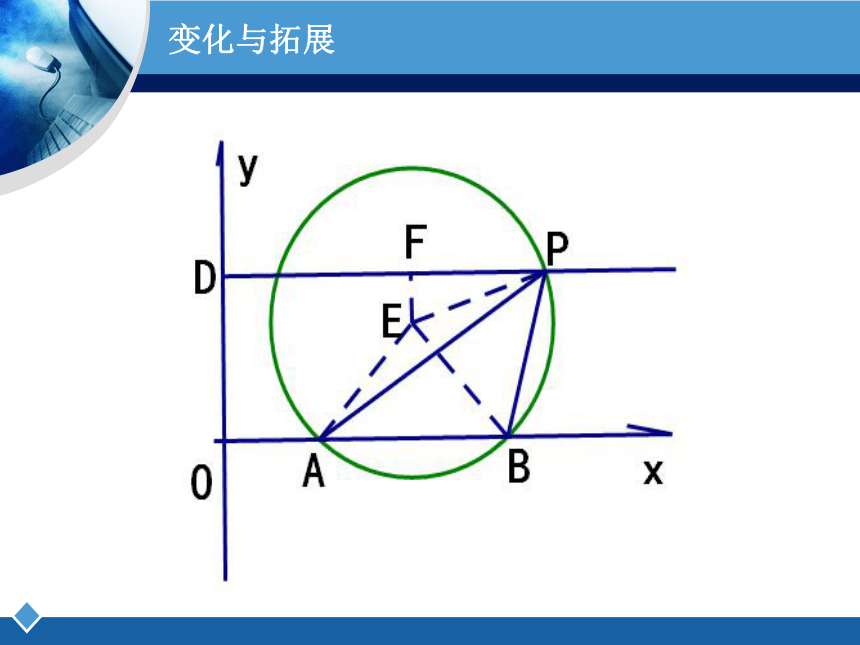
变化与拓展
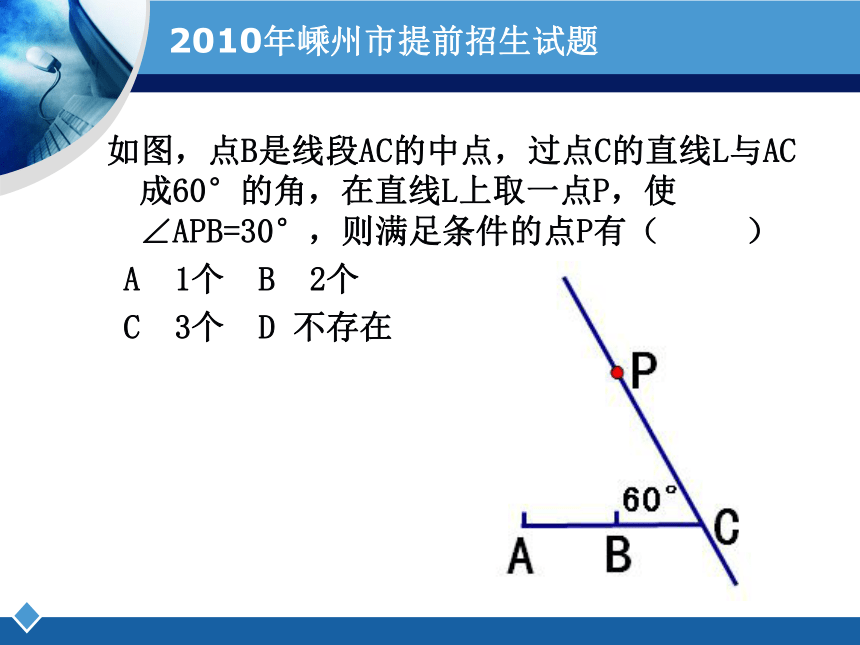
2010年嵊州市提前招生试题
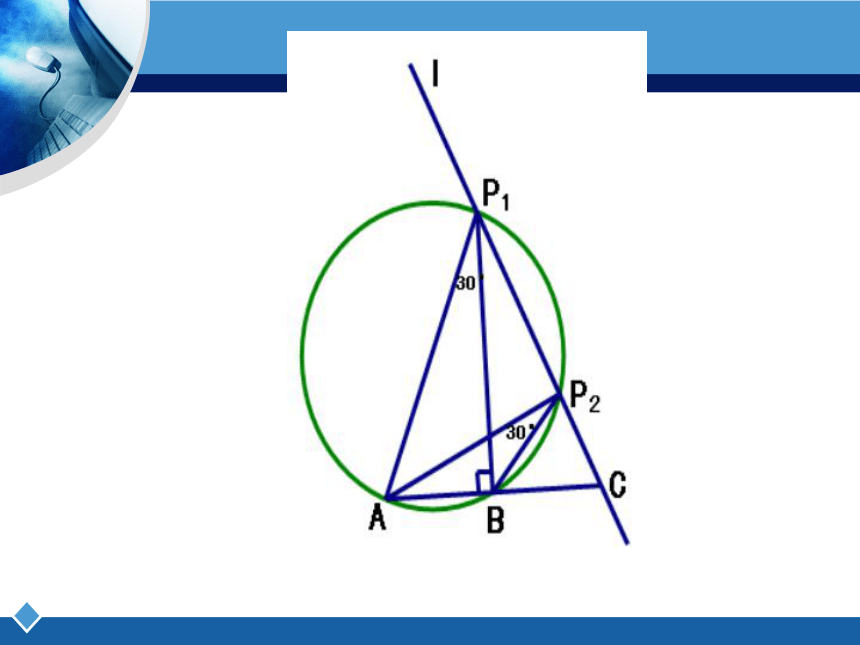
如图,点B是线段AC的中点,过点C的直线L与AC成60°的角,在直线L上取一点P,使∠APB=30°,则满足条件的点P有( )
A 1个 B 2个
C 3个 D 不存在
一、应用举例
问题1
问题 2
问题 3
问题 4
模式的选择与应用
------最值问题
A
B
A’
P
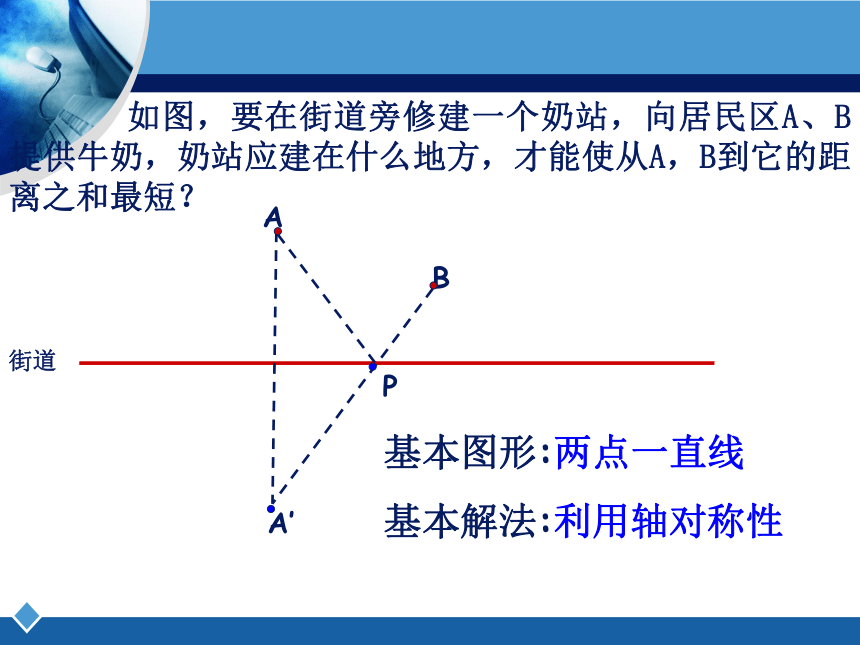
如图,要在街道旁修建一个奶站,向居民区A、B提供牛奶,奶站应建在什么地方,才能使从A,B到它的距离之和最短?
街道
基本图形:两点一直线
基本解法:利用轴对称性
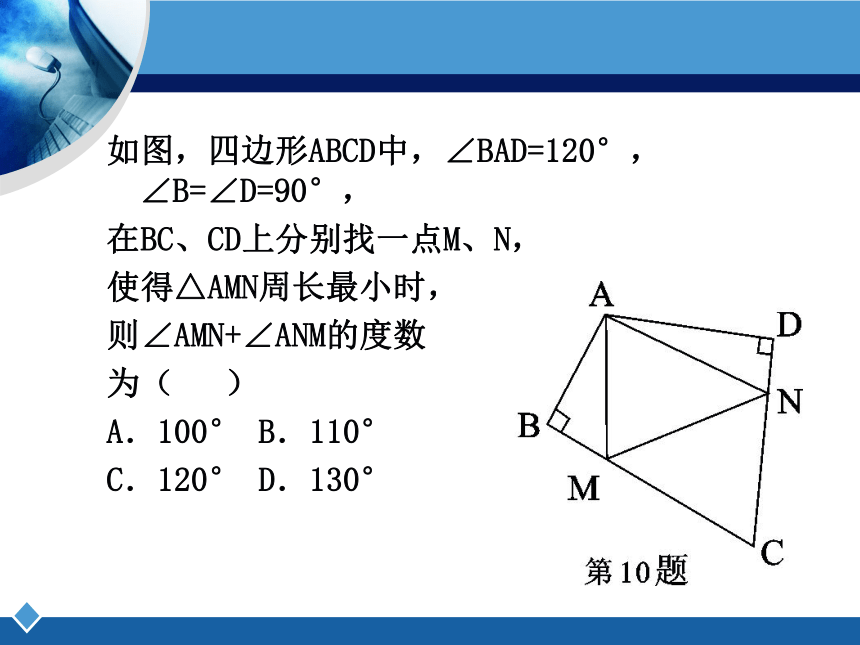
如图,四边形ABCD中,∠BAD=120°,∠B=∠D=90°,
在BC、CD上分别找一点M、N,
使得△AMN周长最小时,
则∠AMN+∠ANM的度数
为( )
A.100° B.110°
C.120° D.130°
A
B
C
D
M
(黑龙江)如图,正方形ABCD中,AB=2,P是对角线AC上任意一点,
P
P
找出基本图形
背景为正方形
(1)若M是AB边上的中点,求PM+PB的最小值
作法与理由:连结BA并延长BA交直线L于点P,点P即所求点。因为|AP-BP|≤AB,当且仅当P是BA延长线与直线交点时, =AB
模式1:(1)已知在直线L的同侧有两点A,B,在直线L上找一点P,使 最大
模式2:已知在直线L的异侧有两点A,B,在直线L上找一点Q,使
最大
L
L
Q
L
L
L
L
L
L
(2011龙岩)如图,∠MON的两边OM、OM上分别有点A、B,且∠MON=30°,OA=8,OD=4 B,C分别是边OM ON上的动点,求AC+BC+BD的最小值
L
(2011 福州)已知,如图,二次函数y=ax2+2ax﹣3a(a≠0)图象的顶点为H,与x轴交于A、B两点(B在A点右侧),点H、B关于直线l: 对称
(1)求A、B两点坐标,并证明点A在直线l上;
(2)求二次函数解析式;
(3)过点B作直线BK∥AH交直线l于K点,M、N分别为直线AH和直线l上的两个动点,连接HN、NM、MK,求HN+NM+MK和的最小值.
L
模式5:直线外一点与直线上各点连接
的所有线段中,垂线段最短。
B
作点N关于直线AD的对称点N′,由对称性知, N′在AC上,连MN′,则MN′=MN,要使BM+MN最小,只要BM+ MN′最小,必须使得BM, MN′在同一直线上,故这个最小值就是过点B作AC的垂线段的长
L
L
如图3,若F1: ,经过变换后, ,点P 是直线 AC 上的动点,求点P到点D的距离和到直线AD的距离之和的最小值.
转化为⊿ABD边AD上的高h.
模式的选择与应用(二)
题目(浙教版八年级上册P47第2题)
如图,在
和
在边BC的延长线上,且
求证:△CAB≌△ECD。
中,AC=CE,点D
第24题图1
(2,2)、
、
坐标系中三角形的面积公式
益阳市中考题
求:△PAB的最大面积
查漏补缺,病理诊断
方法指导,专题教学
如图①,梯形ABCD中,∠C=90°.动点E、F同时从点B出发,点E沿折线 BA—AD—DC运动到点C时停止运动,点F沿BC运动到点C时停止运动,它们运动时的速度都是1 cm/s.设E、F出发t s时,△EBF的面积为y cm2.已知y与t的函数图象如图②所示,其中曲线OM为抛物线的一部分,MN、NP为线段.请根据图中的信息,解答下列问题:(1)梯形上底的长AD=_____cm,梯形ABCD的面积_____cm2;
(2)当点E在BA、DC上运动时,分别求出y与t的函数关系式(注明自变量的取值范围);
(3)当t为何值时,△EBF与梯形ABCD的面积之比为1:2.
题目
16.如图,在平面直角坐标系中,A(1,0)、B(5,0)、C(6,3)、D(0,3),点P为线段CD上一点,
且∠APB=45°,
则点P的坐标
为 .
变化与拓展
2010年嵊州市提前招生试题
如图,点B是线段AC的中点,过点C的直线L与AC成60°的角,在直线L上取一点P,使∠APB=30°,则满足条件的点P有( )
A 1个 B 2个
C 3个 D 不存在
一、应用举例
问题1
问题 2
问题 3
问题 4
模式的选择与应用
------最值问题
A
B
A’
P
如图,要在街道旁修建一个奶站,向居民区A、B提供牛奶,奶站应建在什么地方,才能使从A,B到它的距离之和最短?
街道
基本图形:两点一直线
基本解法:利用轴对称性
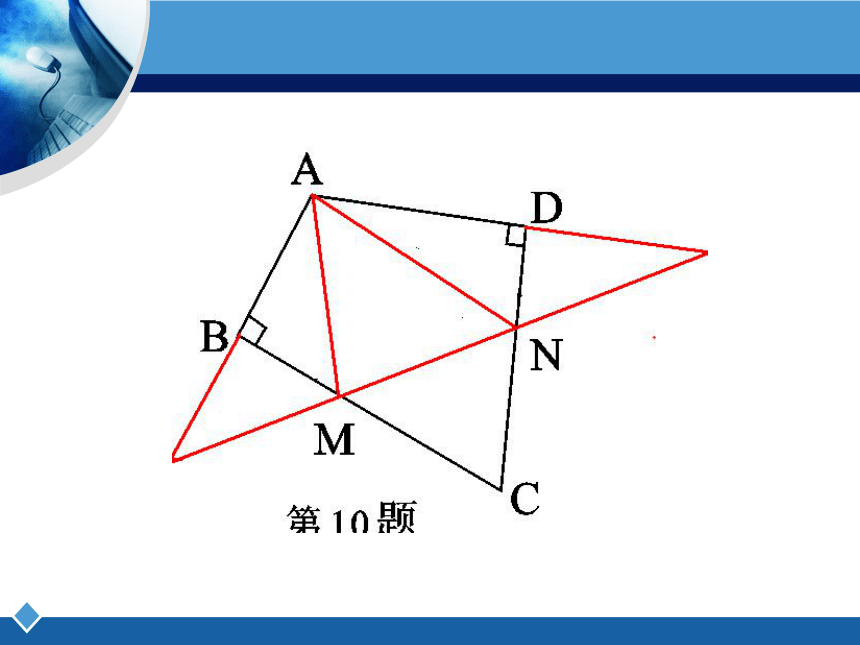
如图,四边形ABCD中,∠BAD=120°,∠B=∠D=90°,
在BC、CD上分别找一点M、N,
使得△AMN周长最小时,
则∠AMN+∠ANM的度数
为( )
A.100° B.110°
C.120° D.130°
A
B
C
D
M
(黑龙江)如图,正方形ABCD中,AB=2,P是对角线AC上任意一点,
P
P
找出基本图形
背景为正方形
(1)若M是AB边上的中点,求PM+PB的最小值
作法与理由:连结BA并延长BA交直线L于点P,点P即所求点。因为|AP-BP|≤AB,当且仅当P是BA延长线与直线交点时, =AB
模式1:(1)已知在直线L的同侧有两点A,B,在直线L上找一点P,使 最大
模式2:已知在直线L的异侧有两点A,B,在直线L上找一点Q,使
最大
L
L
Q
L
L
L
L
L
L
(2011龙岩)如图,∠MON的两边OM、OM上分别有点A、B,且∠MON=30°,OA=8,OD=4 B,C分别是边OM ON上的动点,求AC+BC+BD的最小值
L
(2011 福州)已知,如图,二次函数y=ax2+2ax﹣3a(a≠0)图象的顶点为H,与x轴交于A、B两点(B在A点右侧),点H、B关于直线l: 对称
(1)求A、B两点坐标,并证明点A在直线l上;
(2)求二次函数解析式;
(3)过点B作直线BK∥AH交直线l于K点,M、N分别为直线AH和直线l上的两个动点,连接HN、NM、MK,求HN+NM+MK和的最小值.
L
模式5:直线外一点与直线上各点连接
的所有线段中,垂线段最短。
B
作点N关于直线AD的对称点N′,由对称性知, N′在AC上,连MN′,则MN′=MN,要使BM+MN最小,只要BM+ MN′最小,必须使得BM, MN′在同一直线上,故这个最小值就是过点B作AC的垂线段的长
L
L
如图3,若F1: ,经过变换后, ,点P 是直线 AC 上的动点,求点P到点D的距离和到直线AD的距离之和的最小值.
转化为⊿ABD边AD上的高h.
模式的选择与应用(二)
题目(浙教版八年级上册P47第2题)
如图,在
和
在边BC的延长线上,且
求证:△CAB≌△ECD。
中,AC=CE,点D
第24题图1
(2,2)、
、
坐标系中三角形的面积公式
益阳市中考题
求:△PAB的最大面积
同课章节目录
