初数七下 知识点精讲 垂线(12张PPT)
文档属性
| 名称 | 初数七下 知识点精讲 垂线(12张PPT) |
|
|
| 格式 | pptx | ||
| 文件大小 | 747.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-15 00:00:00 | ||
图片预览


文档简介
垂线
考点聚焦
1.理解垂线的有关概念和表示方法,掌握垂线的画法;
2.会根据垂直进行简单的角的计算。
垂线的定义:
知识梳理
考点一 垂线的定义
两条直线相交成四个角,如果有一个角是直角,那么称这两条直线互相垂直。
注意:
两条线段互相垂直是指这两条线段所在的直线互相垂直。
知识梳理
考点二 垂线的表示方法
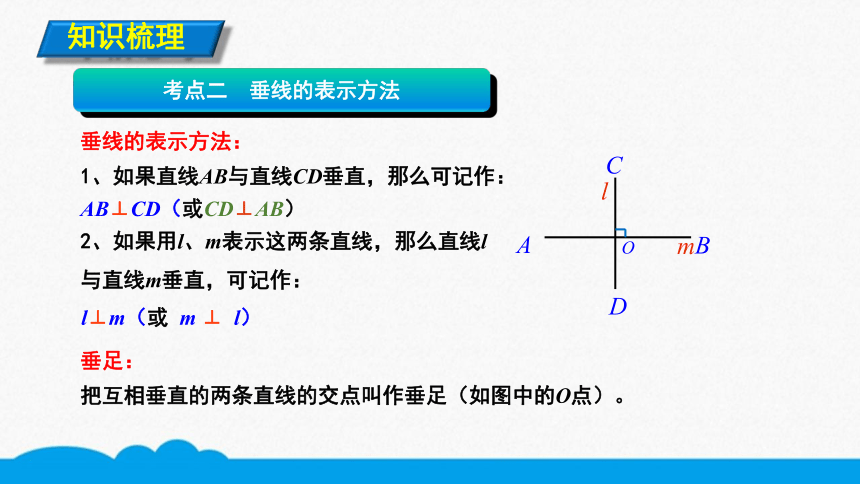
垂线的表示方法:
1、如果直线AB与直线CD垂直,那么可记作:
2、如果用l、m表示这两条直线,那么直线l与直线m垂直,可记作:
把互相垂直的两条直线的交点叫作垂足(如图中的O点)。
AB⊥CD(或CD⊥AB)
l⊥m(或 m ⊥ l)
垂足:
D
A
B
C
O
l
m
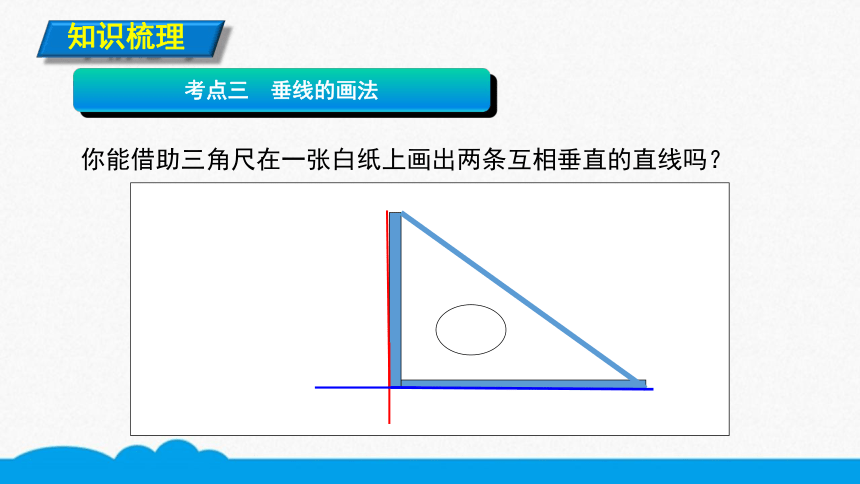
你能借助三角尺在一张白纸上画出两条互相垂直的直线吗?
知识梳理
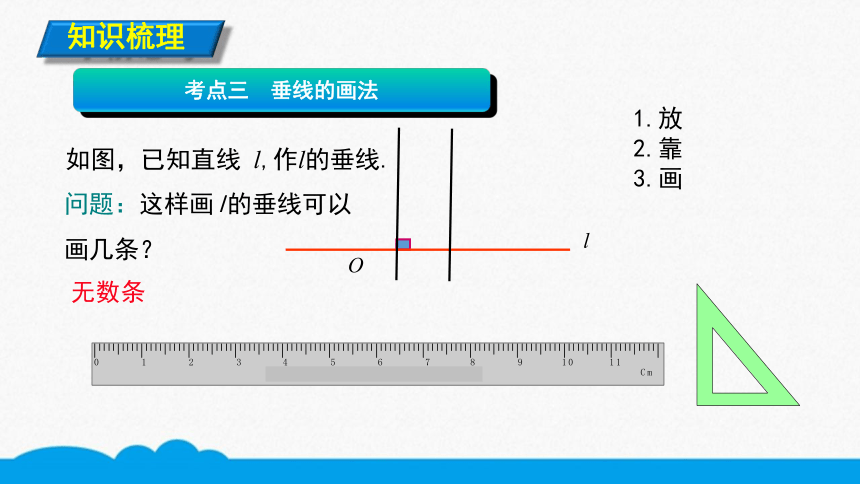
考点三 垂线的画法
问题:这样画l的垂线可以画几条?
1.放
2.靠
3.画
l
O
如图,已知直线 l,作l的垂线.
A
无数条
知识梳理
考点三 垂线的画法
l
A
B
1.放
2.靠
3.移
4.画
如图,已知直线 l 和l上的一点A ,作l的垂线.
问题:这样画l的垂线可以画几条?
一条
知识梳理
考点三 垂线的画法
l
A
B
1.放
2.靠
3.移
4.画
如图,已知直线 l 和l外的一点A ,作l的垂线.
问题:这样画l的垂线可以画几条?
一条
知识梳理
考点三 垂线的画法
典例剖析
由垂线的定义:两条直线相交成四个角,如果有一个角是直角,那么称这两条直线互相垂直。我们得到:直角和90度是等价表示的。
方法点拨
(1)如图1,若直线m、n相交于点O,∠1=90°,则 ;
(2)若直线AB、CD相交于点O,且AB⊥CD,则∠BOD =______。
O
m
n
1
图1
m⊥n
90°
O
C
B
A
解析(2)
D
垂直的角等于90度,一个角的补角加这个角的和等于180度。
方法点拨
典例剖析
如图2,BO⊥AO,∠BOC与∠BOA 的度数之比为1∶5,
那么∠COA=____,∠BOC的补角为______。
72°
162°
B
C
A
O
图2
解:因为∠BOA =90?,
∠BOC?∠BOA =1?5
所以∠BOC=90?×
∠COA=90?-18?=72?
∠BOC的补角:180?-18?=162?
备考技法
1、垂线的定义及表示方法;
2、垂线的画法及基本事实:
(1)已知直线l的垂线能画无数条。
(2)过直线l上的一点A画l的垂线,这样的垂线能画1条。
(3)过直线l外的一点B画l的垂线,这样的垂线能画1条。
垂线
垂足:把互相垂直的两条直线的交点叫作垂足。
定义:两条直线相交成四个角,如果有一个角是直角,那么称这两条直线互相垂直。
思维导图
垂线的画法
考点聚焦
1.理解垂线的有关概念和表示方法,掌握垂线的画法;
2.会根据垂直进行简单的角的计算。
垂线的定义:
知识梳理
考点一 垂线的定义
两条直线相交成四个角,如果有一个角是直角,那么称这两条直线互相垂直。
注意:
两条线段互相垂直是指这两条线段所在的直线互相垂直。
知识梳理
考点二 垂线的表示方法
垂线的表示方法:
1、如果直线AB与直线CD垂直,那么可记作:
2、如果用l、m表示这两条直线,那么直线l与直线m垂直,可记作:
把互相垂直的两条直线的交点叫作垂足(如图中的O点)。
AB⊥CD(或CD⊥AB)
l⊥m(或 m ⊥ l)
垂足:
D
A
B
C
O
l
m
你能借助三角尺在一张白纸上画出两条互相垂直的直线吗?
知识梳理
考点三 垂线的画法
问题:这样画l的垂线可以画几条?
1.放
2.靠
3.画
l
O
如图,已知直线 l,作l的垂线.
A
无数条
知识梳理
考点三 垂线的画法
l
A
B
1.放
2.靠
3.移
4.画
如图,已知直线 l 和l上的一点A ,作l的垂线.
问题:这样画l的垂线可以画几条?
一条
知识梳理
考点三 垂线的画法
l
A
B
1.放
2.靠
3.移
4.画
如图,已知直线 l 和l外的一点A ,作l的垂线.
问题:这样画l的垂线可以画几条?
一条
知识梳理
考点三 垂线的画法
典例剖析
由垂线的定义:两条直线相交成四个角,如果有一个角是直角,那么称这两条直线互相垂直。我们得到:直角和90度是等价表示的。
方法点拨
(1)如图1,若直线m、n相交于点O,∠1=90°,则 ;
(2)若直线AB、CD相交于点O,且AB⊥CD,则∠BOD =______。
O
m
n
1
图1
m⊥n
90°
O
C
B
A
解析(2)
D
垂直的角等于90度,一个角的补角加这个角的和等于180度。
方法点拨
典例剖析
如图2,BO⊥AO,∠BOC与∠BOA 的度数之比为1∶5,
那么∠COA=____,∠BOC的补角为______。
72°
162°
B
C
A
O
图2
解:因为∠BOA =90?,
∠BOC?∠BOA =1?5
所以∠BOC=90?×
∠COA=90?-18?=72?
∠BOC的补角:180?-18?=162?
备考技法
1、垂线的定义及表示方法;
2、垂线的画法及基本事实:
(1)已知直线l的垂线能画无数条。
(2)过直线l上的一点A画l的垂线,这样的垂线能画1条。
(3)过直线l外的一点B画l的垂线,这样的垂线能画1条。
垂线
垂足:把互相垂直的两条直线的交点叫作垂足。
定义:两条直线相交成四个角,如果有一个角是直角,那么称这两条直线互相垂直。
思维导图
垂线的画法
