初数七下 知识点精讲 垂线的性质(8张PPT)
文档属性
| 名称 | 初数七下 知识点精讲 垂线的性质(8张PPT) |
|
|
| 格式 | pptx | ||
| 文件大小 | 675.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-15 00:00:00 | ||
图片预览


文档简介
垂线的性质
考点聚焦
1.理解垂线的有关性质;
2.知道垂线段和点到直线的距离的概念,并会应用
其解决问题。
知识梳理
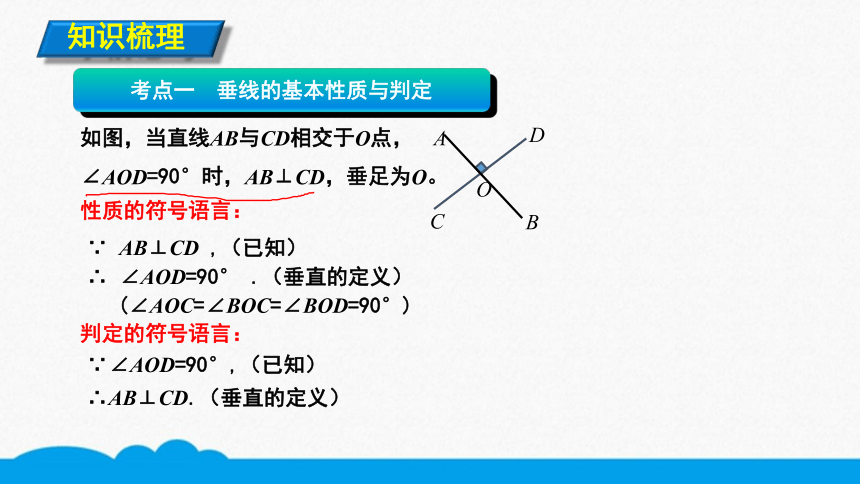
考点一 垂线的基本性质与判定
如图,当直线AB与CD相交于O点,∠AOD=90°时,AB⊥CD,垂足为O。
性质的符号语言:
A
B
C
D
O
∵ AB⊥CD ,(已知)
∴ ∠AOD=90° .(垂直的定义)
(∠AOC=∠BOC=∠BOD=90°)
判定的符号语言:
∵∠AOD=90°,(已知)
∴AB⊥CD.(垂直的定义)
知识梳理
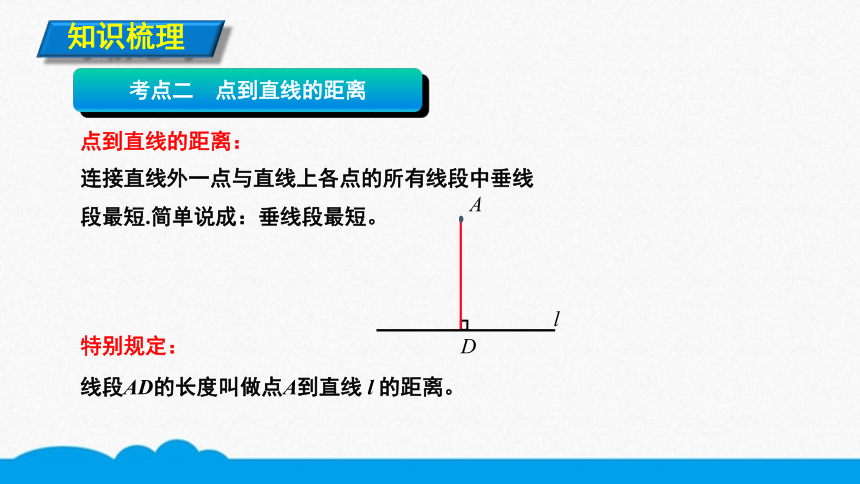
考点二 点到直线的距离
点到直线的距离:
连接直线外一点与直线上各点的所有线段中垂线段最短.简单说成:垂线段最短。
线段AD的长度叫做点A到直线 l 的距离。
特别规定:
D
l
A
典例剖析
在图中标清楚题干中的已知信息,根据垂线的定义和垂线的性质,我们就很容易得到角的度数。
方法点拨
如图,直线BC与MN相交于点O,AO⊥BC,∠BOE=∠NOE,若∠EON=20°,求∠AOM和∠NOC的度数。
解:∵∠BOE=∠NOE
∴∠BON=2∠EON=40°
∴∠NOC=180°-∠BON =180°-40°=140°
∠MOC=∠BON=40°.
∵AO⊥BC,
∴∠AOC=90°,
∠AOM=∠AOC-∠MOC=90°-40°=50°,
∴∠NOC=140°,∠AOM=50°.
解决这类题,除了在图中标清楚题干中的已知信息,还要综合运用垂直,余角,对顶角和角平分线的定义,不断转化角和角之间的运算关系进行计算。
方法点拨
典例剖析
如图,AO⊥FD,OD为∠BOC的平分线,OE为射线OB的反向延长线,若∠AOB=40°,求∠EOF、∠COE的度数。
解:∵AO⊥OD且∠AOB=40°,
∴∠BOD=90°-40°=50°,
∴∠EOF=50°
又∵OD平分∠BOC
A
F
D
O
B
C
E
∴∠DOC=∠BOD=50°,
∴∠COE=180°-50°-50°=80°.
备考技法
1、垂线的性质:在同一平面内,过一点有且只有一条直线与已知直线垂直(垂线段最短)。
2、注意:
(1)“过一点”中的点,可以在已知直线上,也可以在已知直线外;
(2)“有且只有”中,“有”指存在,“只有”指唯一性。
3、点和直线之间的距离:点到直线的垂线段的长度。
点和直线上各点之间的连线中,垂线段最短。
垂线的性质
“有且只有”中,“有”指存在,“只有”指唯一性。
“过一点”中的点,可以在已知直线上,也可以在已知直线外。
思维导图
垂线段最短
考点聚焦
1.理解垂线的有关性质;
2.知道垂线段和点到直线的距离的概念,并会应用
其解决问题。
知识梳理
考点一 垂线的基本性质与判定
如图,当直线AB与CD相交于O点,∠AOD=90°时,AB⊥CD,垂足为O。
性质的符号语言:
A
B
C
D
O
∵ AB⊥CD ,(已知)
∴ ∠AOD=90° .(垂直的定义)
(∠AOC=∠BOC=∠BOD=90°)
判定的符号语言:
∵∠AOD=90°,(已知)
∴AB⊥CD.(垂直的定义)
知识梳理
考点二 点到直线的距离
点到直线的距离:
连接直线外一点与直线上各点的所有线段中垂线段最短.简单说成:垂线段最短。
线段AD的长度叫做点A到直线 l 的距离。
特别规定:
D
l
A
典例剖析
在图中标清楚题干中的已知信息,根据垂线的定义和垂线的性质,我们就很容易得到角的度数。
方法点拨
如图,直线BC与MN相交于点O,AO⊥BC,∠BOE=∠NOE,若∠EON=20°,求∠AOM和∠NOC的度数。
解:∵∠BOE=∠NOE
∴∠BON=2∠EON=40°
∴∠NOC=180°-∠BON =180°-40°=140°
∠MOC=∠BON=40°.
∵AO⊥BC,
∴∠AOC=90°,
∠AOM=∠AOC-∠MOC=90°-40°=50°,
∴∠NOC=140°,∠AOM=50°.
解决这类题,除了在图中标清楚题干中的已知信息,还要综合运用垂直,余角,对顶角和角平分线的定义,不断转化角和角之间的运算关系进行计算。
方法点拨
典例剖析
如图,AO⊥FD,OD为∠BOC的平分线,OE为射线OB的反向延长线,若∠AOB=40°,求∠EOF、∠COE的度数。
解:∵AO⊥OD且∠AOB=40°,
∴∠BOD=90°-40°=50°,
∴∠EOF=50°
又∵OD平分∠BOC
A
F
D
O
B
C
E
∴∠DOC=∠BOD=50°,
∴∠COE=180°-50°-50°=80°.
备考技法
1、垂线的性质:在同一平面内,过一点有且只有一条直线与已知直线垂直(垂线段最短)。
2、注意:
(1)“过一点”中的点,可以在已知直线上,也可以在已知直线外;
(2)“有且只有”中,“有”指存在,“只有”指唯一性。
3、点和直线之间的距离:点到直线的垂线段的长度。
点和直线上各点之间的连线中,垂线段最短。
垂线的性质
“有且只有”中,“有”指存在,“只有”指唯一性。
“过一点”中的点,可以在已知直线上,也可以在已知直线外。
思维导图
垂线段最短
