初数七下 知识点精讲 解一元一次不等式组(8张PPT)
文档属性
| 名称 | 初数七下 知识点精讲 解一元一次不等式组(8张PPT) |
|
|
| 格式 | pptx | ||
| 文件大小 | 685.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-15 00:00:00 | ||
图片预览



文档简介
解一元一次
不等式组
考点聚焦
1.考点:解不等式组,确定解集;
2.题型:填空、选择、解答题的形式都会出现;
3.难度:中等.
知识梳理
考点 解一元一次不等式组
不等式组的解集:不等式组中所有不等式解集的公共部分,叫做不等式组的解集.
解不等式组:求不等式组的解集的过程叫做解不等式组.
定义: 一般地,由几个含有同一个未知数的一元一次不等式所组成的不等式组,叫做一元一次不等式组.
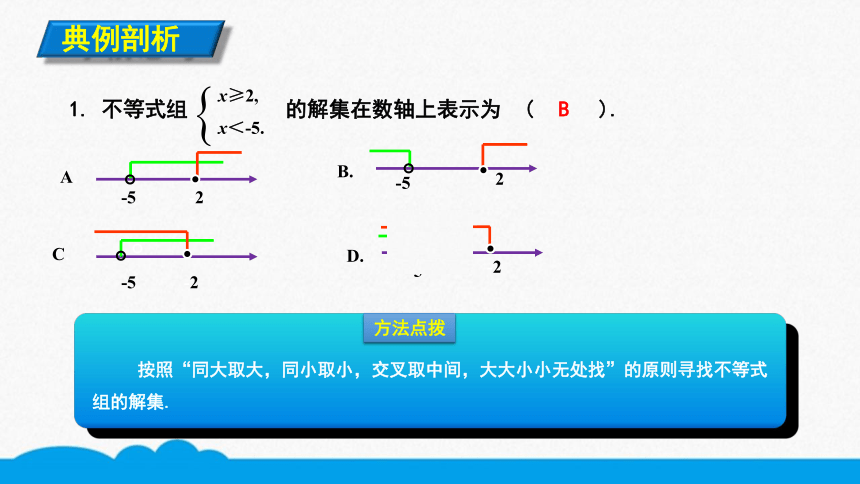
1. 不等式组 的解集在数轴上表示为 ( ).
x≥2,
x<-5.
A.
-5
-2
B.
-5
-2
C.
-5
-2
-2
-5
D.
B
典例剖析
按照“同大取大,同小取小,交叉取中间,大大小小无处找”的原则寻找不等式组的解集.
方法点拨
典例剖析
2. 不等式组 的负整数解是( )。
x≥-2,
x>-3.
A.-2,0,-1
B. -2
C.-2,-1,
D.不能确定.
c
解:同大取大,所以x≥-2,满足负整数解得就只有-2,-1
解不等式组时通常会遇到关键词“整数解”,“负整数解”,注意选择出符合条件的不等式组的解集。
方法点拨
典例剖析
一个长方形的花圃长为x米,宽为70米,如果它的周长大于240米,面积小于7000平方米,你能列出不等式解决这个问题吗?
解:
2(x+70)>240
70x﹤7000
①
②
x<100.
解不等式①得:
解不等式②得:
x>50,
在数轴上表示不等式①、②的解集:
50
100
50
公共部分50{
根据关键词“不大于”,“小于”列不等式,注意不等式组的解集符合实际意义。
方法点拨
备考技法
1、学会用数轴表示一元一次不等式的解。
2、根据同大取大,同小取小,交叉取中间,大大小小无处找的原则解不等式组。
3、解不等式组的注意事项:
(1)注意不等式组的解题方法:分开解,集中判
(2)注意解集在数轴上的表示方法。
(3)会找他们的公共部分,并会用不等式来表示。
思维导图
不等式的解
不等式组的解集
一元一次不等式
一元一次不等式组
不等式组
考点聚焦
1.考点:解不等式组,确定解集;
2.题型:填空、选择、解答题的形式都会出现;
3.难度:中等.
知识梳理
考点 解一元一次不等式组
不等式组的解集:不等式组中所有不等式解集的公共部分,叫做不等式组的解集.
解不等式组:求不等式组的解集的过程叫做解不等式组.
定义: 一般地,由几个含有同一个未知数的一元一次不等式所组成的不等式组,叫做一元一次不等式组.
1. 不等式组 的解集在数轴上表示为 ( ).
x≥2,
x<-5.
A.
-5
-2
B.
-5
-2
C.
-5
-2
-2
-5
D.
B
典例剖析
按照“同大取大,同小取小,交叉取中间,大大小小无处找”的原则寻找不等式组的解集.
方法点拨
典例剖析
2. 不等式组 的负整数解是( )。
x≥-2,
x>-3.
A.-2,0,-1
B. -2
C.-2,-1,
D.不能确定.
c
解:同大取大,所以x≥-2,满足负整数解得就只有-2,-1
解不等式组时通常会遇到关键词“整数解”,“负整数解”,注意选择出符合条件的不等式组的解集。
方法点拨
典例剖析
一个长方形的花圃长为x米,宽为70米,如果它的周长大于240米,面积小于7000平方米,你能列出不等式解决这个问题吗?
解:
2(x+70)>240
70x﹤7000
①
②
x<100.
解不等式①得:
解不等式②得:
x>50,
在数轴上表示不等式①、②的解集:
50
100
50
公共部分50
根据关键词“不大于”,“小于”列不等式,注意不等式组的解集符合实际意义。
方法点拨
备考技法
1、学会用数轴表示一元一次不等式的解。
2、根据同大取大,同小取小,交叉取中间,大大小小无处找的原则解不等式组。
3、解不等式组的注意事项:
(1)注意不等式组的解题方法:分开解,集中判
(2)注意解集在数轴上的表示方法。
(3)会找他们的公共部分,并会用不等式来表示。
思维导图
不等式的解
不等式组的解集
一元一次不等式
一元一次不等式组
