2021-2022学年北师大版数学八年级上册1.1.1 探索勾股定理---同步课件(28张PPT)
文档属性
| 名称 | 2021-2022学年北师大版数学八年级上册1.1.1 探索勾股定理---同步课件(28张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-15 16:46:54 | ||
图片预览

文档简介
1.1 第1课时 探索勾股定理
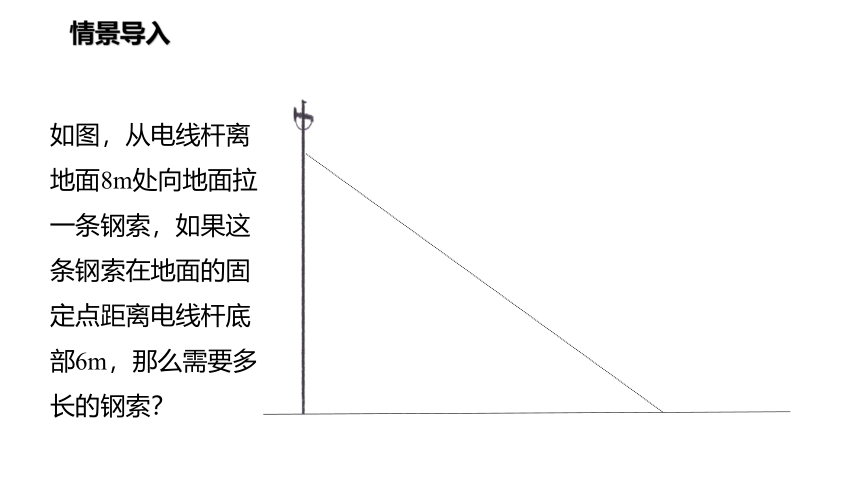
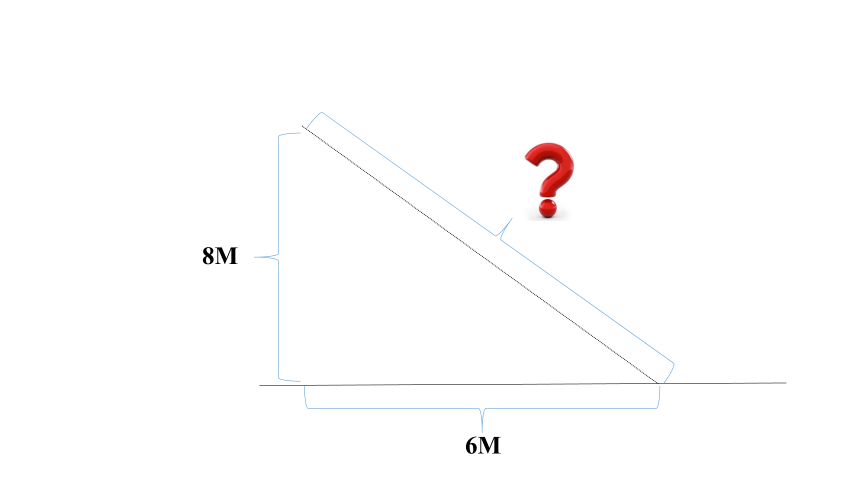
如图,从电线杆离地面8m处向地面拉一条钢索,如果这条钢索在地面的固定点距离电线杆底部6m,那么需要多长的钢索?
情景导入
8M
6M
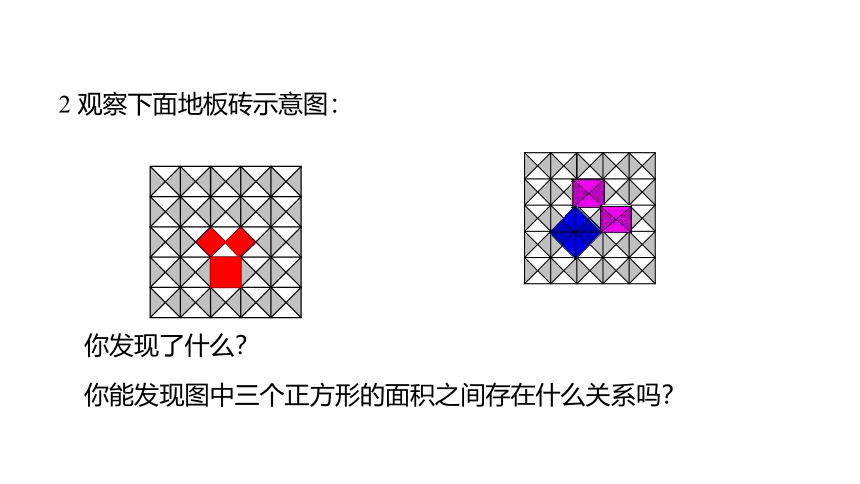
2 观察下面地板砖示意图:
你发现了什么?
你能发现图中三个正方形的面积之间存在什么关系吗?
(图中每一格代表
一平方厘米)
1
2
1
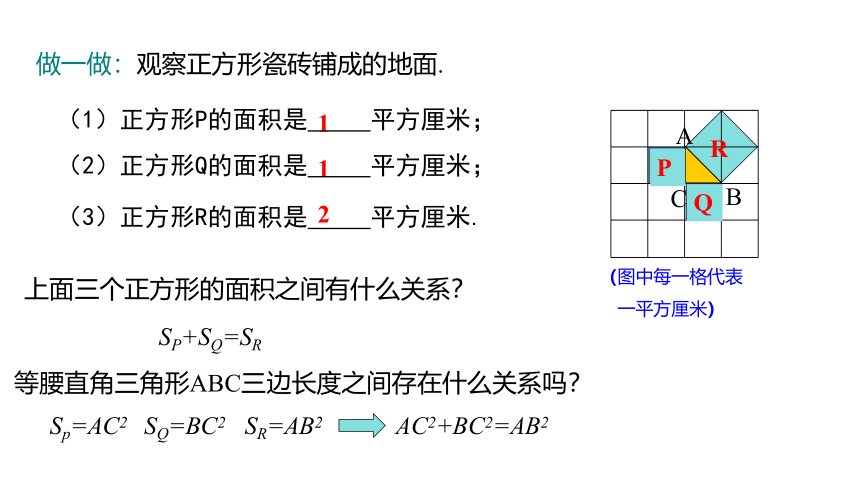
SP+SQ=SR
R
Q
P
A
C
B
AC2+BC2=AB2
等腰直角三角形ABC三边长度之间存在什么关系吗?
Sp=AC2 SQ=BC2 SR=AB2
上面三个正方形的面积之间有什么关系?
做一做:观察正方形瓷砖铺成的地面.
(1)正方形P的面积是 平方厘米;
(2)正方形Q的面积是 平方厘米;
(3)正方形R的面积是 平方厘米.
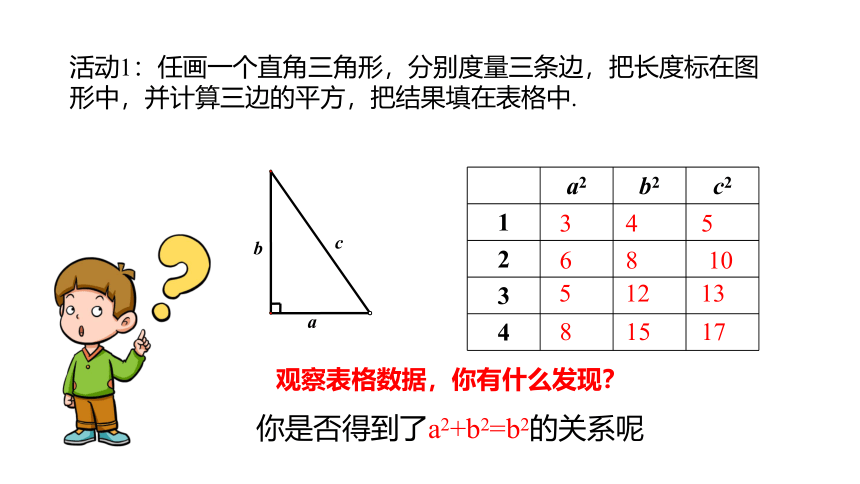
活动1:任画一个直角三角形,分别度量三条边,把长度标在图形中,并计算三边的平方,把结果填在表格中.
{93296810-A885-4BE3-A3E7-6D5BEEA58F35}
a2
b2
c2
1
2
3
4
c
b
a
观察表格数据,你有什么发现?
你是否得到了a2+b2=b2的关系呢
3
5
4
6
10
8
5
13
12
8
17
15
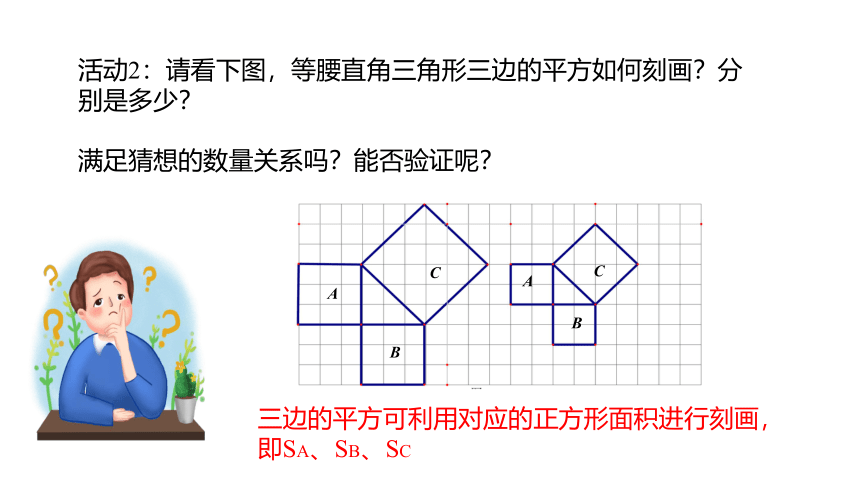
活动2:请看下图,等腰直角三角形三边的平方如何刻画?分别是多少?
满足猜想的数量关系吗?能否验证呢?
A
B
C
A
B
C
三边的平方可利用对应的正方形面积进行刻画,
即SA、SB、SC
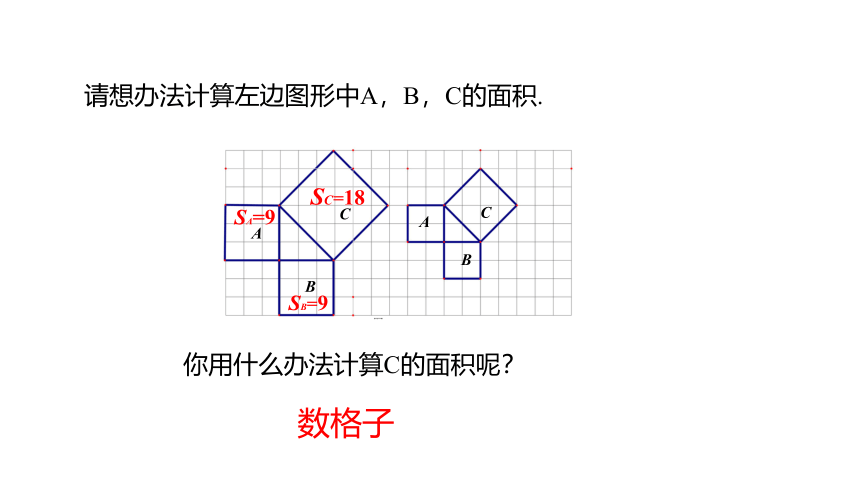
请想办法计算左边图形中A,B,C的面积.
A
B
C
A
B
C
你用什么办法计算C的面积呢?
数格子
SA=9
SC=18
SB=9
C
B
A
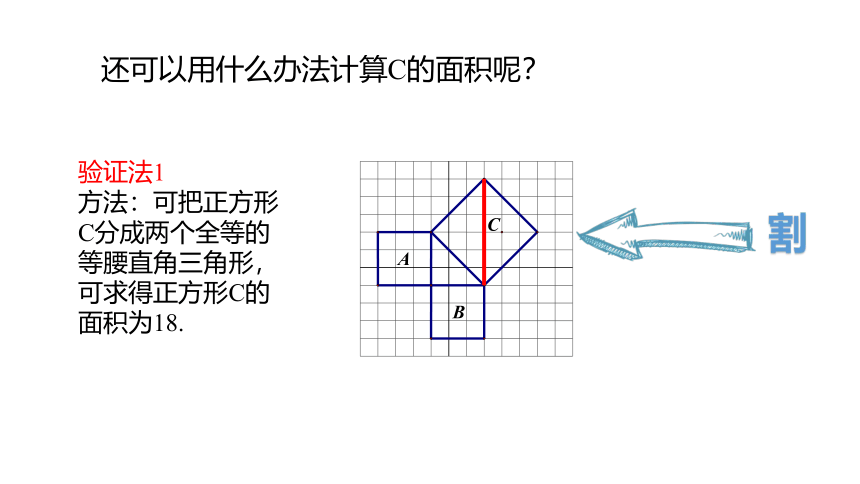
验证法1
方法:可把正方形
C分成两个全等的
等腰直角三角形,
可求得正方形C的
面积为18.
割
还可以用什么办法计算C的面积呢?
C
B
A
验证法2
方法:可把正方形
C分成四个全等的
等腰直角三角形,
可求得正方形C的
面积为18.
割
还可以用什么办法计算C的面积呢?
还可以用什么办法计算C的面积呢?
C
B
A
补
验证法3
方法:可在正方形C
外边圈一个大正方形
用大正方形的面积减
去4个直角三角形的
面积,即可求得正方
形C的面积为18.
C
B
A
由以上计算A,B ,C三
个图形的面积,我们能
得到什么结论?
SA+SB=SC
SC=18
SA=9
SB=9
以上的三角形具有特殊性,都是等腰直角三角形,一般直角三角形是否有这个关系,你还能验证吗?
活动3:看下图,验证是否满足
A
C
B
A
B
C
结论:SA+SB=SC 即:
补
数格子,可以吗?
看下图,验证是否满足
C
B
A
C
B
A
割
结论:SA+SB=SC 即:
勾股定理刻画了直角三角形三边的平方关系,你能用语言描述吗?
直角三角形两直角边的平方和等于斜边的平方.
我国古代学者把直角三角形较短的直角边称为“勾”,较长的直角边称为“股”,斜边称为“弦”.通过以上
探索可以发现:
即
c
b
a
文字语言
获取新知
勾股定理:
在直角三角形中,两条直角边的平方和等于斜边的平方.
在Rt△ABC中,直角边分别是a,b,斜边是c,则:
说明:勾股定理的应用条件是在直角三角形中;勾股定理是刻画直角三角形三边平方的关系.
c
b
a
数学语言
几何语言:
∵在Rt△ABC中 ,∠C=90°,
∴a2+b2=c2(勾股定理).
a
A
B
C
b
c
∟
几何语言
a、b、c可以为负值吗?
例题讲解
解决问题之想一想
如图,从电线杆离地面8m处向地面拉一条钢索,如果这条钢索在地面的固定点距离电线杆底部6m,那么需要多长的钢索?
利用勾股定理
可以得到c?=100,c=10m
求下列直角三角形中未知边的长:
8
x
17
12
5
x
解:由勾股定理可得:
82+ x2=172
即:x2=172-82
x=15
解:由勾股定理可得:
52+ 122= x2
即:x2=52+122
x=13
勾股定理刻画了直角三角形三边的数量关系,由“形”定“数”,有“数与形的第一定理”的美称,体现了“数”与“形”的完美结合,它还能解决哪些问题呢?
我方侦查员小王在距离东西向公路400m处侦查,发现一辆敌方汽车在公路疾驶,他赶紧拿出红外测距仪,测得汽车与他相距400m,10s后,汽车与他相距500m,你能帮小王计算敌方汽车的速度吗?
解:由勾股定理,可以得到AB2=BC2+AC2,也就是5002=BC2+4002,所以BC=300.
敌方汽车10s行驶了300m,那么它1h行驶的距离为300×6×60=108000(m),即它行驶的速度为108km/h
公路
C
B
400m
500m
A
课堂小结
认识
勾股定理
如果直角三角形两直角边长分别为a,b,斜边长为 c ,那么a2+b2=c2
利用勾股定理进行计算
数格子
割补法
测量法
随堂演练
1.图中阴影部分是一个正方形,则此正方形的面积为
36 cm?
8 cm
10 cm
2.求下列图中未知数x、y的值:
解:由勾股定理可得:
81+ 144=x2
即:x2=225 x=15
y2+ 144=169
即:y2=25 y=5
3.如图所示,在Rt△ABC 中,∠C= 90°,AB=10,AC=8,则BC的长度是多少?
解:由勾股定理得:
BC2=AB2-AC2
因为BC>0,所以BC=6.
4.如图所示,在锐角三角形ABC中,高AD=12,边AC=13,BC=14,求AB的长.
解:∵在Rt△ADC中,AD=12,AC=13,
∴由勾股定理,得CD2=AC2-AD2=132-122=52,
∵CD=5.BC=14,
∴BD=14-5=9.
在Rt△ABD中,由勾股定理,得AB2=AD2+BD2=122+92=152,
∴AB=15.
5.如图所示,在四边形ABCD中,∠BAD=90°,∠CBD=90°,AD=4,AB=3,BC=12,求正方形DCEF的面积.
解:∵在Rt△ABD中,由勾股定理,
得AD2+AB2=DB2,
∴42+32=DB2,∴DB=5.
在Rt△BCD中,根据勾股定理,得DB2+BC2=DC2,
∴52+122=DC2,∴DC=13,
∴S正方形DCEF=132=169.
S5=S1+S2=4,
S7=S5+S6=10.
6.已知S1=1,S2=3,S3=2,S4=4,求S5,S6,S7的值.
S6=S3+S4=6,
如图,从电线杆离地面8m处向地面拉一条钢索,如果这条钢索在地面的固定点距离电线杆底部6m,那么需要多长的钢索?
情景导入
8M
6M
2 观察下面地板砖示意图:
你发现了什么?
你能发现图中三个正方形的面积之间存在什么关系吗?
(图中每一格代表
一平方厘米)
1
2
1
SP+SQ=SR
R
Q
P
A
C
B
AC2+BC2=AB2
等腰直角三角形ABC三边长度之间存在什么关系吗?
Sp=AC2 SQ=BC2 SR=AB2
上面三个正方形的面积之间有什么关系?
做一做:观察正方形瓷砖铺成的地面.
(1)正方形P的面积是 平方厘米;
(2)正方形Q的面积是 平方厘米;
(3)正方形R的面积是 平方厘米.
活动1:任画一个直角三角形,分别度量三条边,把长度标在图形中,并计算三边的平方,把结果填在表格中.
{93296810-A885-4BE3-A3E7-6D5BEEA58F35}
a2
b2
c2
1
2
3
4
c
b
a
观察表格数据,你有什么发现?
你是否得到了a2+b2=b2的关系呢
3
5
4
6
10
8
5
13
12
8
17
15
活动2:请看下图,等腰直角三角形三边的平方如何刻画?分别是多少?
满足猜想的数量关系吗?能否验证呢?
A
B
C
A
B
C
三边的平方可利用对应的正方形面积进行刻画,
即SA、SB、SC
请想办法计算左边图形中A,B,C的面积.
A
B
C
A
B
C
你用什么办法计算C的面积呢?
数格子
SA=9
SC=18
SB=9
C
B
A
验证法1
方法:可把正方形
C分成两个全等的
等腰直角三角形,
可求得正方形C的
面积为18.
割
还可以用什么办法计算C的面积呢?
C
B
A
验证法2
方法:可把正方形
C分成四个全等的
等腰直角三角形,
可求得正方形C的
面积为18.
割
还可以用什么办法计算C的面积呢?
还可以用什么办法计算C的面积呢?
C
B
A
补
验证法3
方法:可在正方形C
外边圈一个大正方形
用大正方形的面积减
去4个直角三角形的
面积,即可求得正方
形C的面积为18.
C
B
A
由以上计算A,B ,C三
个图形的面积,我们能
得到什么结论?
SA+SB=SC
SC=18
SA=9
SB=9
以上的三角形具有特殊性,都是等腰直角三角形,一般直角三角形是否有这个关系,你还能验证吗?
活动3:看下图,验证是否满足
A
C
B
A
B
C
结论:SA+SB=SC 即:
补
数格子,可以吗?
看下图,验证是否满足
C
B
A
C
B
A
割
结论:SA+SB=SC 即:
勾股定理刻画了直角三角形三边的平方关系,你能用语言描述吗?
直角三角形两直角边的平方和等于斜边的平方.
我国古代学者把直角三角形较短的直角边称为“勾”,较长的直角边称为“股”,斜边称为“弦”.通过以上
探索可以发现:
即
c
b
a
文字语言
获取新知
勾股定理:
在直角三角形中,两条直角边的平方和等于斜边的平方.
在Rt△ABC中,直角边分别是a,b,斜边是c,则:
说明:勾股定理的应用条件是在直角三角形中;勾股定理是刻画直角三角形三边平方的关系.
c
b
a
数学语言
几何语言:
∵在Rt△ABC中 ,∠C=90°,
∴a2+b2=c2(勾股定理).
a
A
B
C
b
c
∟
几何语言
a、b、c可以为负值吗?
例题讲解
解决问题之想一想
如图,从电线杆离地面8m处向地面拉一条钢索,如果这条钢索在地面的固定点距离电线杆底部6m,那么需要多长的钢索?
利用勾股定理
可以得到c?=100,c=10m
求下列直角三角形中未知边的长:
8
x
17
12
5
x
解:由勾股定理可得:
82+ x2=172
即:x2=172-82
x=15
解:由勾股定理可得:
52+ 122= x2
即:x2=52+122
x=13
勾股定理刻画了直角三角形三边的数量关系,由“形”定“数”,有“数与形的第一定理”的美称,体现了“数”与“形”的完美结合,它还能解决哪些问题呢?
我方侦查员小王在距离东西向公路400m处侦查,发现一辆敌方汽车在公路疾驶,他赶紧拿出红外测距仪,测得汽车与他相距400m,10s后,汽车与他相距500m,你能帮小王计算敌方汽车的速度吗?
解:由勾股定理,可以得到AB2=BC2+AC2,也就是5002=BC2+4002,所以BC=300.
敌方汽车10s行驶了300m,那么它1h行驶的距离为300×6×60=108000(m),即它行驶的速度为108km/h
公路
C
B
400m
500m
A
课堂小结
认识
勾股定理
如果直角三角形两直角边长分别为a,b,斜边长为 c ,那么a2+b2=c2
利用勾股定理进行计算
数格子
割补法
测量法
随堂演练
1.图中阴影部分是一个正方形,则此正方形的面积为
36 cm?
8 cm
10 cm
2.求下列图中未知数x、y的值:
解:由勾股定理可得:
81+ 144=x2
即:x2=225 x=15
y2+ 144=169
即:y2=25 y=5
3.如图所示,在Rt△ABC 中,∠C= 90°,AB=10,AC=8,则BC的长度是多少?
解:由勾股定理得:
BC2=AB2-AC2
因为BC>0,所以BC=6.
4.如图所示,在锐角三角形ABC中,高AD=12,边AC=13,BC=14,求AB的长.
解:∵在Rt△ADC中,AD=12,AC=13,
∴由勾股定理,得CD2=AC2-AD2=132-122=52,
∵CD=5.BC=14,
∴BD=14-5=9.
在Rt△ABD中,由勾股定理,得AB2=AD2+BD2=122+92=152,
∴AB=15.
5.如图所示,在四边形ABCD中,∠BAD=90°,∠CBD=90°,AD=4,AB=3,BC=12,求正方形DCEF的面积.
解:∵在Rt△ABD中,由勾股定理,
得AD2+AB2=DB2,
∴42+32=DB2,∴DB=5.
在Rt△BCD中,根据勾股定理,得DB2+BC2=DC2,
∴52+122=DC2,∴DC=13,
∴S正方形DCEF=132=169.
S5=S1+S2=4,
S7=S5+S6=10.
6.已知S1=1,S2=3,S3=2,S4=4,求S5,S6,S7的值.
S6=S3+S4=6,
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
