2021-2022学年八年级数学北师大版上册第四章 一次函数 4.3.1正比例函数的图象与性质课件 (25张PPT)
文档属性
| 名称 | 2021-2022学年八年级数学北师大版上册第四章 一次函数 4.3.1正比例函数的图象与性质课件 (25张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 347.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-15 22:43:54 | ||
图片预览


文档简介
4.3 第1课时 正比例函数的图象与性质
知识回顾
1、在下列函数
2、函数有哪些表示方法?
图象法、列表法、关系式法
(2),(4)
(2)
三种方法可以相互转化
3、你能将关系式法转化成图象法吗?
什么是函数的图象?
是一次函数的是 , 是正比例函数的是 .
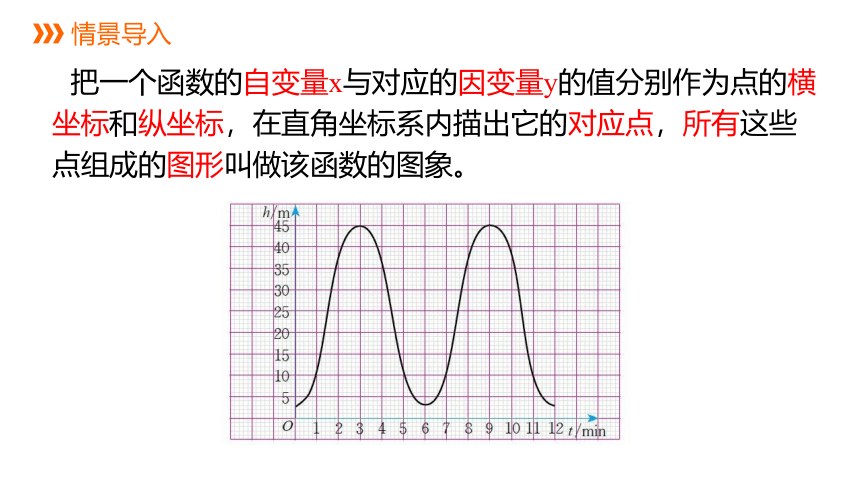
把一个函数的自变量x与对应的因变量y的值分别作为点的横坐标和纵坐标,在直角坐标系内描出它的对应点,所有这些点组成的图形叫做该函数的图象。
情景导入
函数图象的画法步骤
获取新知
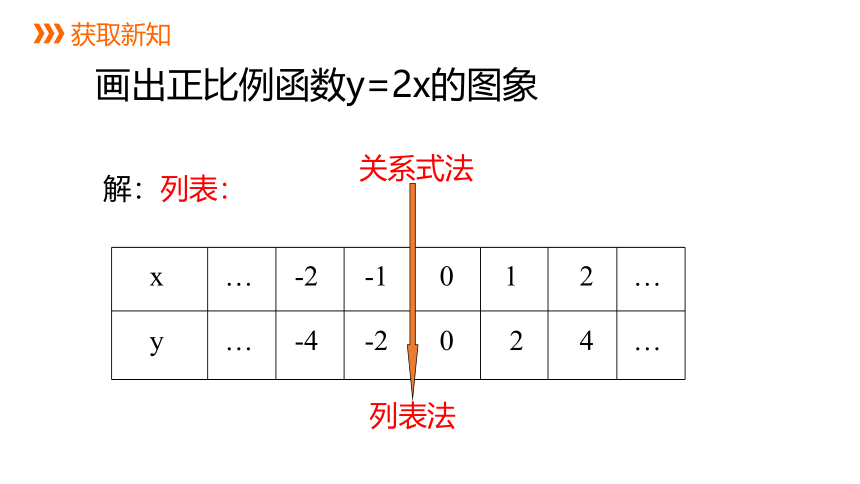
画出正比例函数y=2x的图象
解:列表:
x
y
1
0
0
-1
2
-2
…
…
…
…
2
4
-2
-4
关系式法
列表法
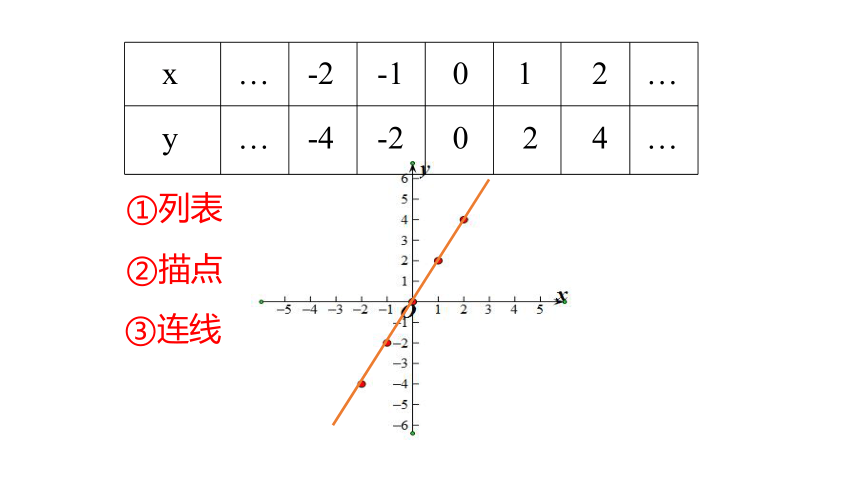
②描点
x
y
1
0
0
-1
2
-2
…
…
…
…
2
4
-2
-4
③连线
①列表
画函数图象的一般步骤:
①列表
②描点
③连线
(1)根据这个步骤画出函数y=-3x的图象
(2)在所作的图象上取几个点,找出它们的横坐标和纵坐标,并验证它们是否都满足关系y=-3x.
y
1
2
4
5
-
1
-
2
-
3
-
4
-
5
-
1
-
2
-
3
-
4
1
4
3
0
y=
-
3x
3
2
x
1
2
5
-
1
-
2
-
3
-
4
-
5
-
1
-
2
-
3
-
4
1
4
3
0
-
3
2
x
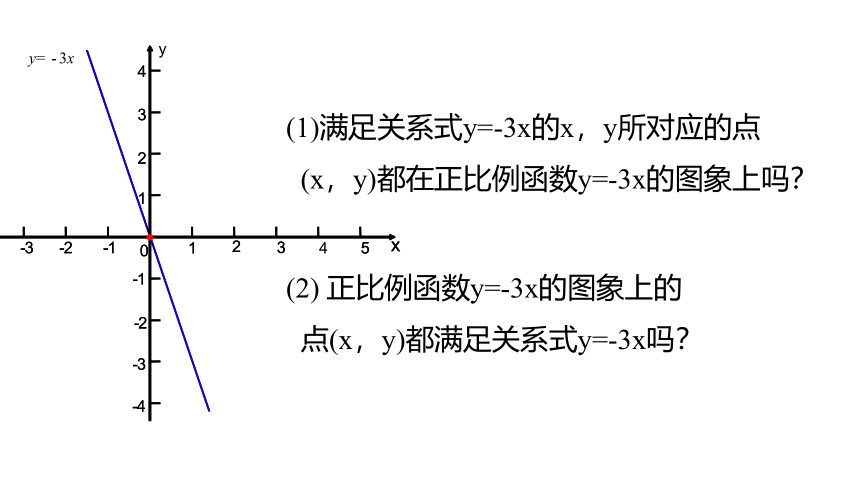
(1)满足关系式y=-3x的x,y所对应的点
(x,y)都在正比例函数y=-3x的图象上吗?
(2) 正比例函数y=-3x的图象上的
点(x,y)都满足关系式y=-3x吗?
y
1
2
4
5
-
1
-
2
-
3
-
4
-
5
-
1
-
2
-
3
-
4
1
4
3
0
y=
-
3x
3
2
x
1
2
5
-
1
-
2
-
3
-
4
-
5
-
1
-
2
-
3
-
4
1
4
3
0
-
3
2
x
y=2x
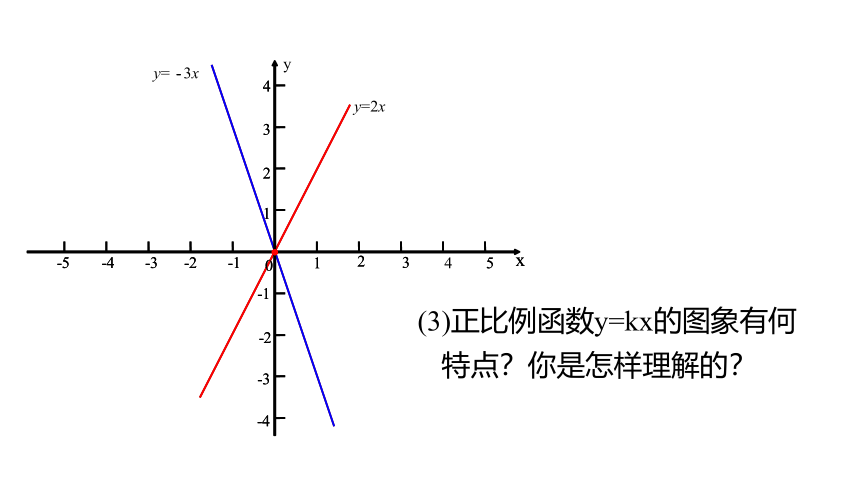
(3)正比例函数y=kx的图象有何特点?你是怎样理解的?
正比例函数y=kx的图象
是一条经过原点的直线。
通过以上学习,画正比例函数图象有无简便的办法?
思考
x
y
0
x
y
0
1
1
y= 2x
y= -3x
-3
2
正比例函数图象经过点(0,0)和点(1,k).
1
k
1
k
y= kx (k>0)
y= kx
(k<0)
y
x
y
x
正比例函数的图像是一条直线,而两点确定一条直线.
画正比例函数的图像时,只需描两个点(0,0)和(1,k),然后过这两个点画一条直线.
例题讲解
例1 在同一直角坐标系内作出y=x, y=3x,y= - x , y=-4x的图象
x
0
1
y=x
0
1
y=3x
0
3
y=-x
0
-1
y=-4x
0
-4
解:列表
观察所画图象,能否进行分类?
能否总结每一类的特征吗?
与同伴交流一下
当k>0时,正比例函数的图像经过第一、三象限,
自变量x逐渐增大时,y的值也随着逐渐增大.
(2) 当k<0时,正比例函数的图像经过第二、四象限,
自变量x逐渐增大时,y的值则随着逐渐减小.
正比例函数y=kx(k≠0)的性质
例2 已知正比例函数y=(m+1)xm2 ,它的图象 经过第几象限?
m+1=2>0
该函数是正比例函数
m2=1
{
∴根据正比例函数的性质,k>0可得该图象经过一、三象限.
解:
∴m=1
(1)正比例函数y=x和y=3x中,随着x值的增大y的值都增加了,其中哪一个增加得更快?你能说明其中的道理吗?
(2)正比例函数y=- x和y=-4x中,随着x值的增大y的值都减小了,其中哪一个减小得更快?你是如何判断的?
|k|越大,直线越陡,直线越靠近y轴.
y=-4x
y=3x
1.正比例函数y=k1x和y=k2x的图象如图,则k1和k2的大小关系是( )
A k1>k2 B k1=k2
C k1y=k1x
y=k2x
x
y
o
A
2.已知正比例函数y=mx的图象经过点(m,4),且y的值随着x值的增大而减小,求m的值.
解:因为函数图象经过点(m,4),所以4=m·m,解得m=±2.
又y的值随着x值的增大而减小,
所以m<0,故m=-2.
练习:
课堂小结
画正比例函数图象的一般步骤:列表、描点、连线
两点作图法:一般取(0,0),(1,k)这两点
性质1
当k>0时,经过第一、三象限;
当k<0时,经过第二、四象限.
性质2
当k>0时,y的值随x值的增大而增大;
当k<0时,y的值随x值的增大而减小.
图象:经过原点的一条直线.
性质3
|k|越大,直线越陡,直线越靠近y轴
性质
图象
正比例函数
随堂演练
1.正比例函数y=3x的大致图象是( )
B
2.已知正比例函数y=3x的图象经过点(1,m),则
m的值为( )
A. B.3
C. D.-3
B
3.对于正比例函数y =(k-2)x,当x 增大时,y 随x 的增大而增大,则k的取值范围 ( )
A.k<2 B.k≤2
C.k>2 D.k≥2
C
4.已知正比例函数y=(2m+4)x.
(1)当m ,函数图象经过第一、三象限;
(2)当m ,y 随x 的增大而减小;
(3)当m ,函数图象经过点(2,10).
>-2
<-2
=0.5
5. 如图分别是函数y=k1 x,y=k2 x,y=k3 x,y=k4 x的图象.
(1)k1 k2,k3 k4(填“>”或“<”或“=”);
(2)用不等号将k1, k2, k3, k4及0依次连接起来.
<
解: k1<k2 <0<k3 <k4
4
2
-2
-4
4
x
y
O
y =k4 x
-4
-2
2
y =k3 x
y =k2 x
y =k1 x
<
6. 已知某小汽车的耗油量是每100km耗油15 L.所用的汽油为5元/ L .
(1)写出汽车行驶途中耗油费y(元)与行程 x(km)之间的函数关系式.
(2)在平面直角坐标系内描出大致的函数图象.
(3)计算该汽车行驶220 km所需油费是多少.
(1)y=5×15x/100,
即 .
解:
(2)
x
0
4
y
0
3
列表
描点
连线
y/元
x/km
1 2 3 4 5 6 7
6
5
4
3
2
1
O
(3)当x=220时,
答:该汽车行驶220 km所需油费是165元.
(元).
知识回顾
1、在下列函数
2、函数有哪些表示方法?
图象法、列表法、关系式法
(2),(4)
(2)
三种方法可以相互转化
3、你能将关系式法转化成图象法吗?
什么是函数的图象?
是一次函数的是 , 是正比例函数的是 .
把一个函数的自变量x与对应的因变量y的值分别作为点的横坐标和纵坐标,在直角坐标系内描出它的对应点,所有这些点组成的图形叫做该函数的图象。
情景导入
函数图象的画法步骤
获取新知
画出正比例函数y=2x的图象
解:列表:
x
y
1
0
0
-1
2
-2
…
…
…
…
2
4
-2
-4
关系式法
列表法
②描点
x
y
1
0
0
-1
2
-2
…
…
…
…
2
4
-2
-4
③连线
①列表
画函数图象的一般步骤:
①列表
②描点
③连线
(1)根据这个步骤画出函数y=-3x的图象
(2)在所作的图象上取几个点,找出它们的横坐标和纵坐标,并验证它们是否都满足关系y=-3x.
y
1
2
4
5
-
1
-
2
-
3
-
4
-
5
-
1
-
2
-
3
-
4
1
4
3
0
y=
-
3x
3
2
x
1
2
5
-
1
-
2
-
3
-
4
-
5
-
1
-
2
-
3
-
4
1
4
3
0
-
3
2
x
(1)满足关系式y=-3x的x,y所对应的点
(x,y)都在正比例函数y=-3x的图象上吗?
(2) 正比例函数y=-3x的图象上的
点(x,y)都满足关系式y=-3x吗?
y
1
2
4
5
-
1
-
2
-
3
-
4
-
5
-
1
-
2
-
3
-
4
1
4
3
0
y=
-
3x
3
2
x
1
2
5
-
1
-
2
-
3
-
4
-
5
-
1
-
2
-
3
-
4
1
4
3
0
-
3
2
x
y=2x
(3)正比例函数y=kx的图象有何特点?你是怎样理解的?
正比例函数y=kx的图象
是一条经过原点的直线。
通过以上学习,画正比例函数图象有无简便的办法?
思考
x
y
0
x
y
0
1
1
y= 2x
y= -3x
-3
2
正比例函数图象经过点(0,0)和点(1,k).
1
k
1
k
y= kx (k>0)
y= kx
(k<0)
y
x
y
x
正比例函数的图像是一条直线,而两点确定一条直线.
画正比例函数的图像时,只需描两个点(0,0)和(1,k),然后过这两个点画一条直线.
例题讲解
例1 在同一直角坐标系内作出y=x, y=3x,y= - x , y=-4x的图象
x
0
1
y=x
0
1
y=3x
0
3
y=-x
0
-1
y=-4x
0
-4
解:列表
观察所画图象,能否进行分类?
能否总结每一类的特征吗?
与同伴交流一下
当k>0时,正比例函数的图像经过第一、三象限,
自变量x逐渐增大时,y的值也随着逐渐增大.
(2) 当k<0时,正比例函数的图像经过第二、四象限,
自变量x逐渐增大时,y的值则随着逐渐减小.
正比例函数y=kx(k≠0)的性质
例2 已知正比例函数y=(m+1)xm2 ,它的图象 经过第几象限?
m+1=2>0
该函数是正比例函数
m2=1
{
∴根据正比例函数的性质,k>0可得该图象经过一、三象限.
解:
∴m=1
(1)正比例函数y=x和y=3x中,随着x值的增大y的值都增加了,其中哪一个增加得更快?你能说明其中的道理吗?
(2)正比例函数y=- x和y=-4x中,随着x值的增大y的值都减小了,其中哪一个减小得更快?你是如何判断的?
|k|越大,直线越陡,直线越靠近y轴.
y=-4x
y=3x
1.正比例函数y=k1x和y=k2x的图象如图,则k1和k2的大小关系是( )
A k1>k2 B k1=k2
C k1
y=k2x
x
y
o
A
2.已知正比例函数y=mx的图象经过点(m,4),且y的值随着x值的增大而减小,求m的值.
解:因为函数图象经过点(m,4),所以4=m·m,解得m=±2.
又y的值随着x值的增大而减小,
所以m<0,故m=-2.
练习:
课堂小结
画正比例函数图象的一般步骤:列表、描点、连线
两点作图法:一般取(0,0),(1,k)这两点
性质1
当k>0时,经过第一、三象限;
当k<0时,经过第二、四象限.
性质2
当k>0时,y的值随x值的增大而增大;
当k<0时,y的值随x值的增大而减小.
图象:经过原点的一条直线.
性质3
|k|越大,直线越陡,直线越靠近y轴
性质
图象
正比例函数
随堂演练
1.正比例函数y=3x的大致图象是( )
B
2.已知正比例函数y=3x的图象经过点(1,m),则
m的值为( )
A. B.3
C. D.-3
B
3.对于正比例函数y =(k-2)x,当x 增大时,y 随x 的增大而增大,则k的取值范围 ( )
A.k<2 B.k≤2
C.k>2 D.k≥2
C
4.已知正比例函数y=(2m+4)x.
(1)当m ,函数图象经过第一、三象限;
(2)当m ,y 随x 的增大而减小;
(3)当m ,函数图象经过点(2,10).
>-2
<-2
=0.5
5. 如图分别是函数y=k1 x,y=k2 x,y=k3 x,y=k4 x的图象.
(1)k1 k2,k3 k4(填“>”或“<”或“=”);
(2)用不等号将k1, k2, k3, k4及0依次连接起来.
<
解: k1<k2 <0<k3 <k4
4
2
-2
-4
4
x
y
O
y =k4 x
-4
-2
2
y =k3 x
y =k2 x
y =k1 x
<
6. 已知某小汽车的耗油量是每100km耗油15 L.所用的汽油为5元/ L .
(1)写出汽车行驶途中耗油费y(元)与行程 x(km)之间的函数关系式.
(2)在平面直角坐标系内描出大致的函数图象.
(3)计算该汽车行驶220 km所需油费是多少.
(1)y=5×15x/100,
即 .
解:
(2)
x
0
4
y
0
3
列表
描点
连线
y/元
x/km
1 2 3 4 5 6 7
6
5
4
3
2
1
O
(3)当x=220时,
答:该汽车行驶220 km所需油费是165元.
(元).
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
