5.2.1代入消元法课件 2021-2022学年北师大版八年级数学上册(17张)
文档属性
| 名称 | 5.2.1代入消元法课件 2021-2022学年北师大版八年级数学上册(17张) |  | |
| 格式 | pptx | ||
| 文件大小 | 221.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-16 10:09:36 | ||
图片预览





文档简介
5.2 第1课时 代入消元法
知识回顾
1:什么是二元一次方程?
答:含有两个未知数,并且所含未知数的项的次数都是1的方程叫做二元一次方程.
2、解方程:2(x-3)=8
答案:x=7
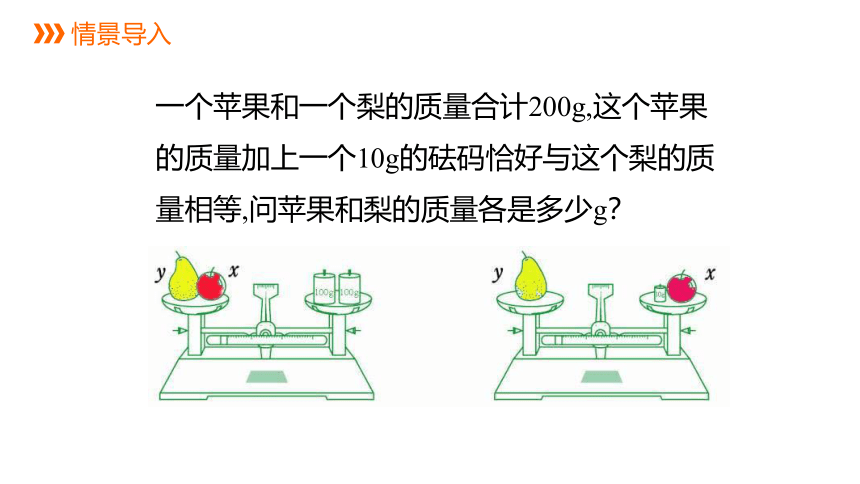
情景导入
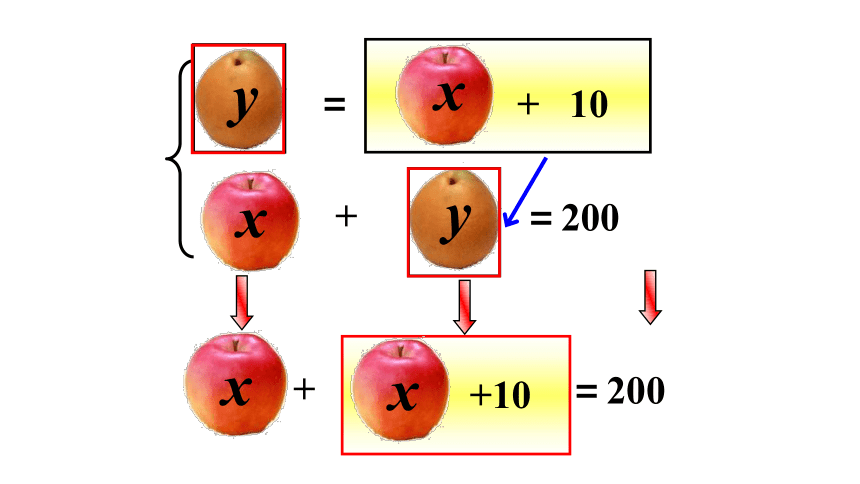
一个苹果和一个梨的质量合计200g,这个苹果的质量加上一个10g的砝码恰好与这个梨的质量相等,问苹果和梨的质量各是多少g?
+
=200
x
y
=
+ 10
x
y
+10
+
=200
x
x
x + y = 200
y = x + 10
(x+10)
x +( x +10) = 200
①
②
x = 95
y = 105
∴方程组 的解是
y = x + 10
x + y = 200
x = 95,
y =105.
求方程组解的过程叫做解方程组
将未知数的个数由多化少,逐一解决的思想,叫做消元思想.
转化
要点归纳
解二元一次方程组的基本思路“消元”
二元一次方程组
一元一次方程
消元
转化
用“代入”的方法进行“消元”,这种解方程组的方法称为代入消元法,简称代入法.
代入法是解二元一次方程组常用的方法之一.
获取新知
在本章第一节课中老牛和小马各驮了多少个包裹的问题中,需要解二元一次方程组
①
②
由①,得 y=x-2.③
由于方程组中相同的字母代表同一对象,所以方程②中的y也等于x-2,可以用x-2代替方程②中的y.这样有
x+1=2( x-2 -1).④
解所得的一元一次方程④,得x=7.
再把x=7代入③,得y=5.
我们得到二元一次方程组的解
因此,老牛驮了7个包裹,小马驮了5个包裹.
把二元化为一元了
例题讲解
例1 解方程组
3x+2y=14 ①
x=y+3 ②
解:将②代入①,得 3(y+3)+2y=14
3y+9+2y=14
5y=5
y=1
将y=1代入②, 得 x=4
所以原方程组的解是
注:想知道答案对不对?最后把求出的解代入原方程组检验就可以了
直接给出x=y+3
例2 解方程组
2x+3y=16, ①
x+4y=13. ②
解:由② ,得 x=13 - 4y. ③
将③代入① ,得 2(13 - 4y)+3y=16,
26 –8y +3y =16,
-5y= -10,
y=2.
y=2时 , x=5
∴
方程组没直接给出x或y等式
将②移项恒等变形为③
将恒等变形后的③代入①中求y值
x=2
y=5
上面解方程组的基本思路是什么?主要步骤有哪些?
基本思路 “消元”(把“二元”变为“一元”)
主要步骤:
1、将方程组中的一个方程的某个未知数用含有另外一个未知数的表达式表示出来;
2、将表示出来的未知数代入另一个方程中,从而消去一个未知数,化二元一次方程组为一元一次方程,解出其中的解;
课堂小结
解二元一次方程组
基本思路“消元”
代入法解二元一次方程组的一般步骤
变:用含一个未知数的式子表示另一个未知数
代:用这个式子替代另一个方程中相应未知数
求:求出两个未知数的值
写:写出方程组的解
D
1.已知方程组 用代入法消去y后的方程是( )
A.x+x-1=3
B.x+2x-1=3
C.x+x-2=3
D.x+2(x-1)=3
y=x-1
x+2y=3
随堂演练
2.二元一次方程组 的解是( )
A.
B.
C.
D.
D
3.解方程组:
x+y=1
2x+y=3
2x+y=4
5x-2y=1
解:(1)
x+y=1 ①
2x+y=3 ②
由①得y=1-x.③
把③代入②,得2x+1-x=3,
解得x=2.
把x=2代入③,得y=-1.所以原方程组的解为
x=2
y=-1
x+y=1 ①
2x+y=3 ②
2x+y=4 ①
5x-2y=1 ②
由①得y=4-2x.③
把③代入②,得5x-2(4-2x)=1,
解得x=1.
把x=1代入③,得y=2.所以原方程组的解为
x=1
y=2
(2)
4.李大叔去年承包了10亩地种植甲、乙两种蔬菜,共获利18000元,其中甲种蔬菜每亩获利2000元,乙种蔬菜每亩获利1500元,李大叔去年甲、乙两种蔬菜各种植多少亩?
解: 设甲、乙两种蔬菜各种植了x、y亩,依题意得:
x+y=10 ①
2000x+1500y=18000 ②
将由①得 y=10-x . ③
将③代入②,得 2000x+1500(10-x)=18000 .
解得 x=6.
将x=6代入③,得y=4.
答:李大叔去年甲、乙两种蔬菜各种植了6亩、4亩.
知识回顾
1:什么是二元一次方程?
答:含有两个未知数,并且所含未知数的项的次数都是1的方程叫做二元一次方程.
2、解方程:2(x-3)=8
答案:x=7
情景导入
一个苹果和一个梨的质量合计200g,这个苹果的质量加上一个10g的砝码恰好与这个梨的质量相等,问苹果和梨的质量各是多少g?
+
=200
x
y
=
+ 10
x
y
+10
+
=200
x
x
x + y = 200
y = x + 10
(x+10)
x +( x +10) = 200
①
②
x = 95
y = 105
∴方程组 的解是
y = x + 10
x + y = 200
x = 95,
y =105.
求方程组解的过程叫做解方程组
将未知数的个数由多化少,逐一解决的思想,叫做消元思想.
转化
要点归纳
解二元一次方程组的基本思路“消元”
二元一次方程组
一元一次方程
消元
转化
用“代入”的方法进行“消元”,这种解方程组的方法称为代入消元法,简称代入法.
代入法是解二元一次方程组常用的方法之一.
获取新知
在本章第一节课中老牛和小马各驮了多少个包裹的问题中,需要解二元一次方程组
①
②
由①,得 y=x-2.③
由于方程组中相同的字母代表同一对象,所以方程②中的y也等于x-2,可以用x-2代替方程②中的y.这样有
x+1=2( x-2 -1).④
解所得的一元一次方程④,得x=7.
再把x=7代入③,得y=5.
我们得到二元一次方程组的解
因此,老牛驮了7个包裹,小马驮了5个包裹.
把二元化为一元了
例题讲解
例1 解方程组
3x+2y=14 ①
x=y+3 ②
解:将②代入①,得 3(y+3)+2y=14
3y+9+2y=14
5y=5
y=1
将y=1代入②, 得 x=4
所以原方程组的解是
注:想知道答案对不对?最后把求出的解代入原方程组检验就可以了
直接给出x=y+3
例2 解方程组
2x+3y=16, ①
x+4y=13. ②
解:由② ,得 x=13 - 4y. ③
将③代入① ,得 2(13 - 4y)+3y=16,
26 –8y +3y =16,
-5y= -10,
y=2.
y=2时 , x=5
∴
方程组没直接给出x或y等式
将②移项恒等变形为③
将恒等变形后的③代入①中求y值
x=2
y=5
上面解方程组的基本思路是什么?主要步骤有哪些?
基本思路 “消元”(把“二元”变为“一元”)
主要步骤:
1、将方程组中的一个方程的某个未知数用含有另外一个未知数的表达式表示出来;
2、将表示出来的未知数代入另一个方程中,从而消去一个未知数,化二元一次方程组为一元一次方程,解出其中的解;
课堂小结
解二元一次方程组
基本思路“消元”
代入法解二元一次方程组的一般步骤
变:用含一个未知数的式子表示另一个未知数
代:用这个式子替代另一个方程中相应未知数
求:求出两个未知数的值
写:写出方程组的解
D
1.已知方程组 用代入法消去y后的方程是( )
A.x+x-1=3
B.x+2x-1=3
C.x+x-2=3
D.x+2(x-1)=3
y=x-1
x+2y=3
随堂演练
2.二元一次方程组 的解是( )
A.
B.
C.
D.
D
3.解方程组:
x+y=1
2x+y=3
2x+y=4
5x-2y=1
解:(1)
x+y=1 ①
2x+y=3 ②
由①得y=1-x.③
把③代入②,得2x+1-x=3,
解得x=2.
把x=2代入③,得y=-1.所以原方程组的解为
x=2
y=-1
x+y=1 ①
2x+y=3 ②
2x+y=4 ①
5x-2y=1 ②
由①得y=4-2x.③
把③代入②,得5x-2(4-2x)=1,
解得x=1.
把x=1代入③,得y=2.所以原方程组的解为
x=1
y=2
(2)
4.李大叔去年承包了10亩地种植甲、乙两种蔬菜,共获利18000元,其中甲种蔬菜每亩获利2000元,乙种蔬菜每亩获利1500元,李大叔去年甲、乙两种蔬菜各种植多少亩?
解: 设甲、乙两种蔬菜各种植了x、y亩,依题意得:
x+y=10 ①
2000x+1500y=18000 ②
将由①得 y=10-x . ③
将③代入②,得 2000x+1500(10-x)=18000 .
解得 x=6.
将x=6代入③,得y=4.
答:李大叔去年甲、乙两种蔬菜各种植了6亩、4亩.
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
