5.4 应用二元一次方程组 增收节支-同步课件 2021-2022学年八年级数学北师大版上册(18张)
文档属性
| 名称 | 5.4 应用二元一次方程组 增收节支-同步课件 2021-2022学年八年级数学北师大版上册(18张) |  | |
| 格式 | pptx | ||
| 文件大小 | 288.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-16 10:11:59 | ||
图片预览






文档简介
5.4 应用二元一次方程组——增收节支
知识回顾
1.一种商品进价为150元,售价为165元,则该商品的利润为_____元;
2.一种商品进价为150元,售价为165元,则该商品的利润率为______;
3.一种商品标价为150元,打八折后的售价为____元;
4.一种商品标价为200元,当打______折后的售价为170元.
15
10﹪
120
8.5
5.某工厂去年的总收入是x万元,今年的总产值比去年增加了20%,则今年的总收入是__________万元;
6.若该厂去年的总支出为y万元,今年的总支出比去年减少了10%,则今年的总支出是__________万元;
7.若该厂今年的利润为780万元,那么由5, 6可得方程___________________________.
(1+20%) x
(1+20%) x- (1-10%) y=780
(1-10%) y
问1:增长(亏损)率问题的公式?
问2:银行利率问题中的公式?(利息、本金、利率)
原量×(1+增长率)=新量
原量×(1-亏损率)=新量
利息=本金×利率×期数(时间)
本息和=本金+利息
利润:总产值-总支出
利润率:(总产值-总支出)/总产值×100%
根据上述公式,我们可以列出二元一次方程组,解决实际问题.
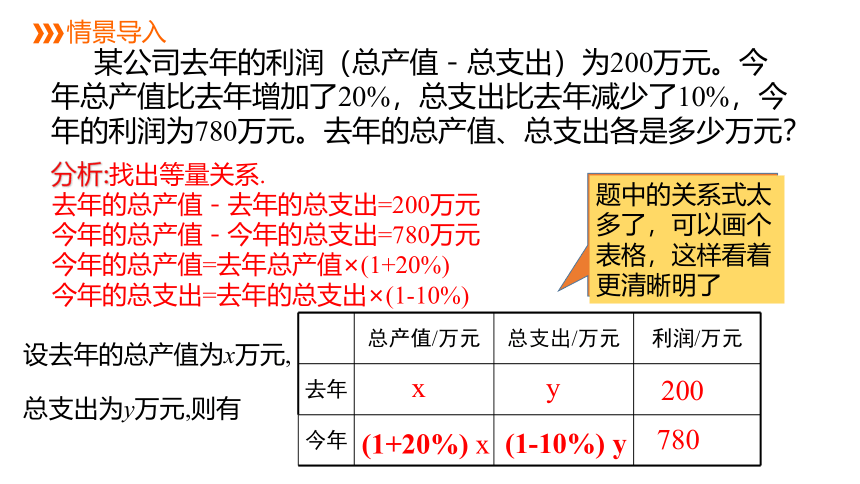
某公司去年的利润(总产值-总支出)为200万元。今年总产值比去年增加了20%,总支出比去年减少了10%,今年的利润为780万元。去年的总产值、总支出各是多少万元?
分析:找出等量关系.
去年的总产值-去年的总支出=200万元
今年的总产值-今年的总支出=780万元
今年的总产值=去年总产值×(1+20%)
今年的总支出=去年的总支出×(1-10%)
题中的关系式太多了,可以画个表格,这样看着更清晰明了
设去年的总产值为x万元,
总支出为y万元,则有
总产值/万元
总支出/万元
利润/万元
去年
今年
x
y
200
780
(1-10%) y
(1+20%) x
情景导入
解:设去年的总产值为x万元,总支出为y万元,
则今年的总产值=(1+20%)x万元,
今年的总支出=(1-10%)y万元。
由题意得:
x-y=200 ①
(1+20%)x-(1-10%)y=780 ②
解得
x=2000
y=1800
答:去年的总收入为2000万元, 总支出为1800万元。
根据列出来的关系表格可以快速的列出二元一次方程组
例题讲解
例 医院用甲、乙两种原料为手术后的病人配制营养品,每克甲原料含0.5单位蛋白质和1单位铁质,每克乙原料含0.7单位蛋白质和0.4单位铁质, 若病人每餐需要35单位蛋白质和40单位铁质, 那么每餐甲、乙原料各多少克恰好满足病人的需要?
分析:找出等量关系式.
每餐甲原料中含蛋白质量=0.5×每餐甲原料的质量
每餐乙原料中含蛋白质量=0.7×每餐乙原料的质量
每餐甲原料中含蛋白质量+每餐乙原料中含蛋白质量=35
所以每餐需甲原料28 g,乙原料30 g.
根据题意,得方程组
0.5x+0.7y=35
x+0.4y=40
解为:
解:设每餐甲、乙原料各x g、y g
甲原料x g
乙原料y g
所配的营养品
其中所含蛋白质
其中所含铁质
0.5x
x
0.7y
0.4y
35
40
获取新知
实际问题
设未知数、找等量关系、
列方程(组)
数学问题
[方程(组)]
解方程(组)
数学问题的解
双检验
实际问题的答案
例题讲解
如图,长青化工厂与A,B两地有公路、铁路相连,这家工厂从A地购买一批每吨1000元的原料运回工厂,制成每吨8 000元的产品运到B地.已知公路运价为1.5 元/(吨·千米),铁路运价为1.2元/(吨·千米),这两次运输共支出公路运费15000元,铁路运费97200元,这批产品的销售款比原料费与运输费的和多多少元?
分析:销售款与产品数量有关,原料费与原材料有关.设制成x吨产品,购买y吨原料.根据题意填写下表:
1.5× 20x
1.2× 110x
8 000x
1.5× 10y
1.2× 120y
1 000y
15 000
97 200
价 值(元)
铁路运费(元)
公路运费(元)
合 计
原料y吨
产品x吨
解:根据图表,列出方程组
解方程组得
x=300,
y=400.
8 000x-1 000y-15 000-97 200
=8000×300-1 000×400-15 000-97 200
=1 887 800(元)
答:这批产品的销售款比原料费与运输费的和多1887800元.
1.5 × 20x+ 1.5×10y=15 000,
1.2 × 110x+ 1.2×120y=97 200.
课堂小结
列方程组解决实际问题
随堂演练
1.某公司购买甲、乙两种货物,设甲、乙两种货物的进货
价分别为x元和y元.若已知两种货物的进货价共30000元,
则可列方程__________;若共获利3150元,已知甲种货物的
利润率是10%,乙种货物的利润率是11%,则可列方程
_______________,由此可得方程组______________.
x+y=30000
10%x+11%y=3150
x+y=30000
10%x+11%y=3150
2.某市现有人口42万人,计划一年后城镇人口增加0.8%,农村人口增加1.1%,这样全市人口将增加1%,则这个城市现有城镇人口和农村人口的数量分别为( )
A.28万,14万 B.24万,18万
C.14万,28万 D.18万,24万
C
3.今年五一期间,某市外来与外出旅游的总人数为226万人,
分别比去年同期增长30%和20%,去年同期外来旅游比外出旅
游的人数多20万人.求该市今年外来和外出旅游的人数.
解:设该市去年外来旅游的人数为x万人,外出旅游的人数为y万人.
根据题意,得
解得
x-y=20
(1+30%)x+(1+20%)y=226
x=100
y=80
所以(1+30%)x=(1+30%)×100=130,
(1+20%)y=(1+20%)×80=96.
答:该市今年外来和外出旅游的人数分别是130万人和96万人.
知识回顾
1.一种商品进价为150元,售价为165元,则该商品的利润为_____元;
2.一种商品进价为150元,售价为165元,则该商品的利润率为______;
3.一种商品标价为150元,打八折后的售价为____元;
4.一种商品标价为200元,当打______折后的售价为170元.
15
10﹪
120
8.5
5.某工厂去年的总收入是x万元,今年的总产值比去年增加了20%,则今年的总收入是__________万元;
6.若该厂去年的总支出为y万元,今年的总支出比去年减少了10%,则今年的总支出是__________万元;
7.若该厂今年的利润为780万元,那么由5, 6可得方程___________________________.
(1+20%) x
(1+20%) x- (1-10%) y=780
(1-10%) y
问1:增长(亏损)率问题的公式?
问2:银行利率问题中的公式?(利息、本金、利率)
原量×(1+增长率)=新量
原量×(1-亏损率)=新量
利息=本金×利率×期数(时间)
本息和=本金+利息
利润:总产值-总支出
利润率:(总产值-总支出)/总产值×100%
根据上述公式,我们可以列出二元一次方程组,解决实际问题.
某公司去年的利润(总产值-总支出)为200万元。今年总产值比去年增加了20%,总支出比去年减少了10%,今年的利润为780万元。去年的总产值、总支出各是多少万元?
分析:找出等量关系.
去年的总产值-去年的总支出=200万元
今年的总产值-今年的总支出=780万元
今年的总产值=去年总产值×(1+20%)
今年的总支出=去年的总支出×(1-10%)
题中的关系式太多了,可以画个表格,这样看着更清晰明了
设去年的总产值为x万元,
总支出为y万元,则有
总产值/万元
总支出/万元
利润/万元
去年
今年
x
y
200
780
(1-10%) y
(1+20%) x
情景导入
解:设去年的总产值为x万元,总支出为y万元,
则今年的总产值=(1+20%)x万元,
今年的总支出=(1-10%)y万元。
由题意得:
x-y=200 ①
(1+20%)x-(1-10%)y=780 ②
解得
x=2000
y=1800
答:去年的总收入为2000万元, 总支出为1800万元。
根据列出来的关系表格可以快速的列出二元一次方程组
例题讲解
例 医院用甲、乙两种原料为手术后的病人配制营养品,每克甲原料含0.5单位蛋白质和1单位铁质,每克乙原料含0.7单位蛋白质和0.4单位铁质, 若病人每餐需要35单位蛋白质和40单位铁质, 那么每餐甲、乙原料各多少克恰好满足病人的需要?
分析:找出等量关系式.
每餐甲原料中含蛋白质量=0.5×每餐甲原料的质量
每餐乙原料中含蛋白质量=0.7×每餐乙原料的质量
每餐甲原料中含蛋白质量+每餐乙原料中含蛋白质量=35
所以每餐需甲原料28 g,乙原料30 g.
根据题意,得方程组
0.5x+0.7y=35
x+0.4y=40
解为:
解:设每餐甲、乙原料各x g、y g
甲原料x g
乙原料y g
所配的营养品
其中所含蛋白质
其中所含铁质
0.5x
x
0.7y
0.4y
35
40
获取新知
实际问题
设未知数、找等量关系、
列方程(组)
数学问题
[方程(组)]
解方程(组)
数学问题的解
双检验
实际问题的答案
例题讲解
如图,长青化工厂与A,B两地有公路、铁路相连,这家工厂从A地购买一批每吨1000元的原料运回工厂,制成每吨8 000元的产品运到B地.已知公路运价为1.5 元/(吨·千米),铁路运价为1.2元/(吨·千米),这两次运输共支出公路运费15000元,铁路运费97200元,这批产品的销售款比原料费与运输费的和多多少元?
分析:销售款与产品数量有关,原料费与原材料有关.设制成x吨产品,购买y吨原料.根据题意填写下表:
1.5× 20x
1.2× 110x
8 000x
1.5× 10y
1.2× 120y
1 000y
15 000
97 200
价 值(元)
铁路运费(元)
公路运费(元)
合 计
原料y吨
产品x吨
解:根据图表,列出方程组
解方程组得
x=300,
y=400.
8 000x-1 000y-15 000-97 200
=8000×300-1 000×400-15 000-97 200
=1 887 800(元)
答:这批产品的销售款比原料费与运输费的和多1887800元.
1.5 × 20x+ 1.5×10y=15 000,
1.2 × 110x+ 1.2×120y=97 200.
课堂小结
列方程组解决实际问题
随堂演练
1.某公司购买甲、乙两种货物,设甲、乙两种货物的进货
价分别为x元和y元.若已知两种货物的进货价共30000元,
则可列方程__________;若共获利3150元,已知甲种货物的
利润率是10%,乙种货物的利润率是11%,则可列方程
_______________,由此可得方程组______________.
x+y=30000
10%x+11%y=3150
x+y=30000
10%x+11%y=3150
2.某市现有人口42万人,计划一年后城镇人口增加0.8%,农村人口增加1.1%,这样全市人口将增加1%,则这个城市现有城镇人口和农村人口的数量分别为( )
A.28万,14万 B.24万,18万
C.14万,28万 D.18万,24万
C
3.今年五一期间,某市外来与外出旅游的总人数为226万人,
分别比去年同期增长30%和20%,去年同期外来旅游比外出旅
游的人数多20万人.求该市今年外来和外出旅游的人数.
解:设该市去年外来旅游的人数为x万人,外出旅游的人数为y万人.
根据题意,得
解得
x-y=20
(1+30%)x+(1+20%)y=226
x=100
y=80
所以(1+30%)x=(1+30%)×100=130,
(1+20%)y=(1+20%)×80=96.
答:该市今年外来和外出旅游的人数分别是130万人和96万人.
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
