人教版三年级上册数学9 数学广角——集合课件(31张PPT)
文档属性
| 名称 | 人教版三年级上册数学9 数学广角——集合课件(31张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 5.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-15 21:15:06 | ||
图片预览







文档简介
(共30张PPT)
人教版数学三年级(上)
数学广角——集合
9
1.经历解决问题的过程,了解简单的集合知识,初步感受它的意义。
2.学会借助维恩图,利用集合的思想方法来解决较简单的实际问题,从而感受数学与生活之间的相互关系。
3.培养乐于观察,合作学习的意识和学习的兴趣。
学习目标
【重点】
理解集合的意义,了解维恩图。
【难点】
能利用集合思想解决问题。
课堂导入
脑筋急转弯。
两位妈妈和两个女儿一同去看电影(每人都得买一张票),可是她们只买了3张票,便顺利地进了电影院。这是为什么?
姥姥
妈妈
女儿
妈妈
女儿
探究新知
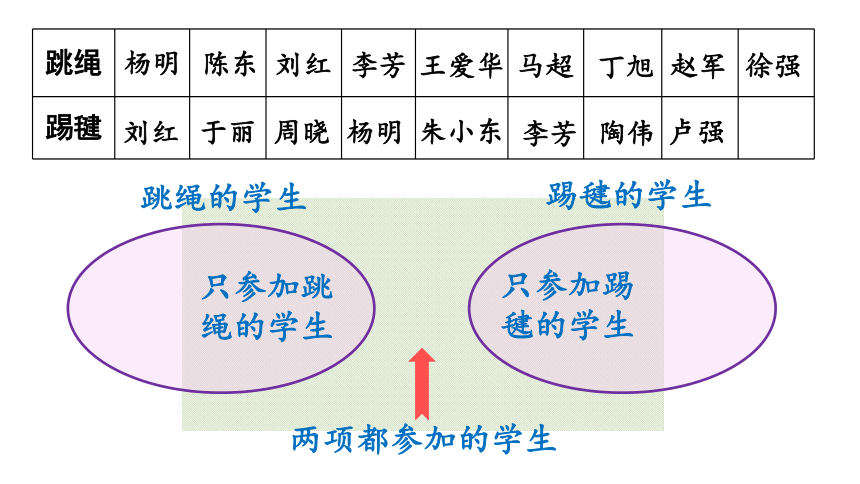
下面是三(1)班参加跳绳、踢毽的学生名单。
参加这两项比赛的共有多少人?
跳绳
踢毽
杨明
陈东
刘红
李芳
王爱华
马超
丁旭
赵军
徐强
杨明
刘红
于丽
周晓
朱小东
陶伟
李芳
卢强
1
跳绳的有9人,踢毽的有8人。
跳绳
踢毽
杨明
陈东
刘红
李芳
王爱华
马超
丁旭
赵军
徐强
杨明
刘红
于丽
周晓
朱小东
陶伟
李芳
卢强
一共有17人。
可是参加这两项比赛的没有17人呀?
我发现有的人两项比赛都参加了。
跳绳
踢毽
杨明
陈东
刘红
李芳
王爱华
马超
丁旭
赵军
徐强
杨明
刘红
于丽
周晓
朱小东
陶伟
李芳
卢强
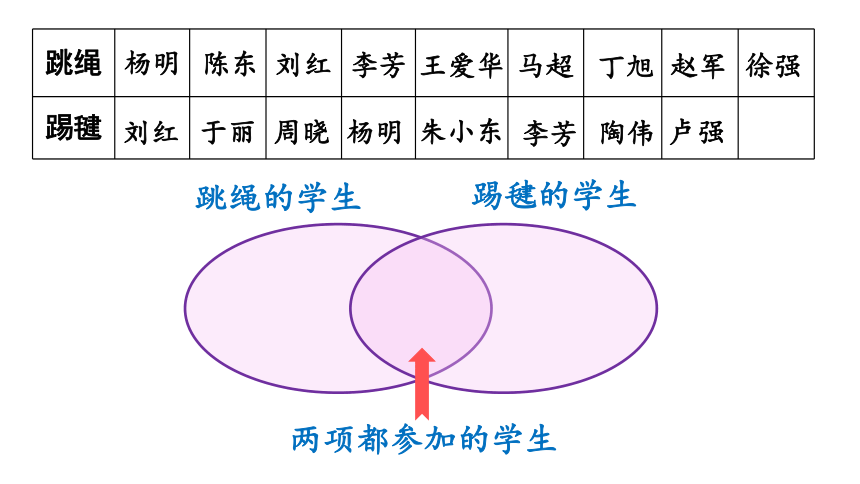
怎样表示能清楚地看出来呢?
我把两项比赛都参加的人连起来,有3个重复的。
跳绳
踢毽
杨明
陈东
刘红
李芳
王爱华
马超
丁旭
赵军
徐强
杨明
刘红
于丽
周晓
朱小东
陶伟
李芳
卢强
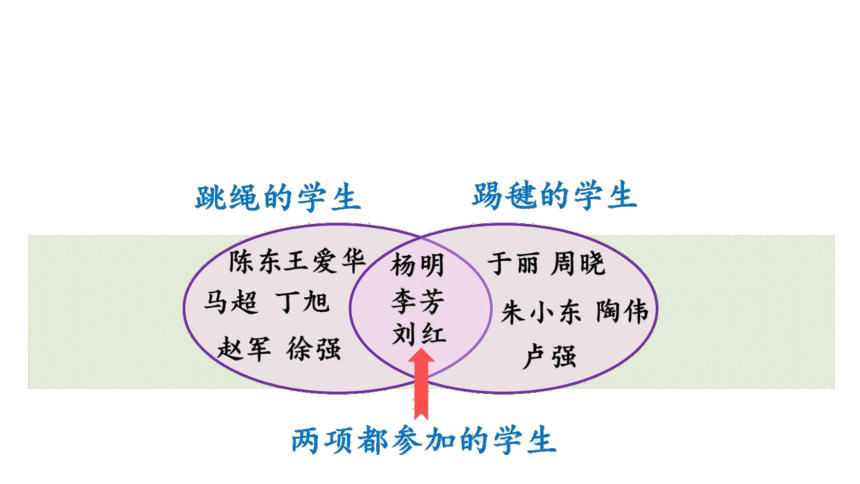
用图表示就清楚了
跳绳
踢毽
杨明
陈东
刘红
李芳
王爱华
马超
丁旭
赵军
徐强
杨明
刘红
于丽
周晓
朱小东
陶伟
李芳
卢强
两项都参加的学生
只参加跳绳的学生
只参加踢毽的学生
跳绳的学生
踢毽的学生
跳绳
踢毽
杨明
陈东
刘红
李芳
王爱华
马超
丁旭
赵军
徐强
杨明
刘红
于丽
周晓
朱小东
陶伟
李芳
卢强
两项都参加的学生
跳绳的学生
踢毽的学生
把指定的具有某种性质的事物看作一个整体,这个整体就是一个集合。
想一想,可以怎样列式解答?
在数学中,我们经常用平面上封闭曲线的内部代表集合,这种图称为维恩图。
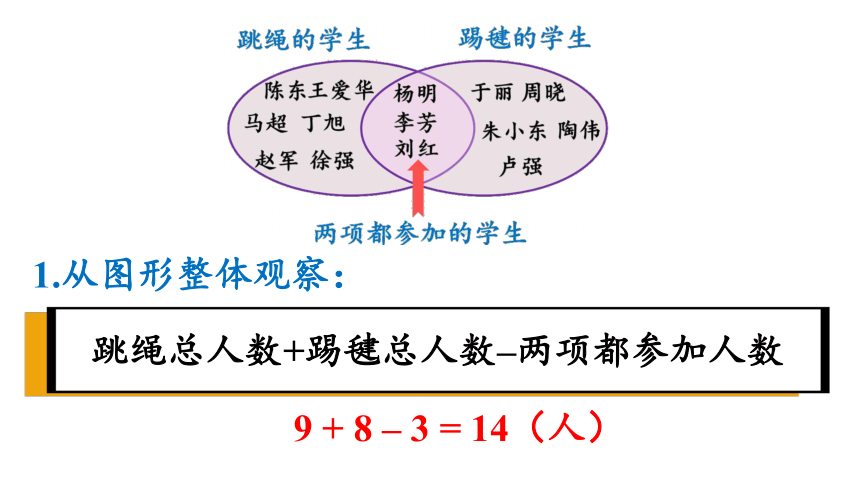
跳绳总人数+踢毽总人数–两项都参加人数
9 + 8 – 3 = 14(人)
1.从图形整体观察:
只参加跳绳人数+踢毽总人数
9 – 3 + 8 = 14(人)
2.从图形左侧入手观察:
8 – 3 + 9 = 14(人)
只参加踢毽人数+跳绳总人数
3.从图形右侧入手观察:
两项都参加人数 + 只参加跳绳人数 + 只参加踢毽人数
4.从图形中心入手观察:
3 +(9 – 3)+(8 – 3)= 14(人)
答:参加比赛的共有14人。
参加这两项比赛的共有多少人?
9 + 8 – 3 = 14(人)
3 +(9 – 3)+(8 – 3)= 14(人)
9 – 3 + 8 = 14(人)
8 – 3 + 9 = 14(人)
课堂练习
教材第105页“做一做”
1.把下面动物的序号填写在合适的圈里。
会游泳的
会飞的
表示什么?
做一做
①
②
③
④
⑤
⑥
⑦
⑧
⑨
⑩
教材第105页“做一做”
会游泳的
会飞的
表示什么?
①
②
③
④
⑤
⑥
⑦
⑧
⑨
⑩
既会游泳又会飞的
2.
(1)既荣获“语文之星”又荣获“数学之星”的
有( )人。
6
做一做
2.
(2)上光荣榜的一共有( )人。
19
做一做
13 + 12 – 6 = 19(人)
3.下面三(1)班同学喜欢球类运动的情况。
喜欢篮球
喜欢足球
喜欢篮球
喜欢足球
既喜欢篮球又喜欢足球
(1)把图补充完整。
陈明
张旭
刘东
刘红
李平
赵霞
张伟
刘东
苏军
李丽
李丽
卢强
王鹏
陶伟
陈明
马涛
王鹏
3.下面三(1)班同学喜欢球类运动的情况。
喜欢篮球
喜欢足球
陈明
张旭
刘东
刘红
李平
赵霞
张伟
刘东
苏军
李丽
李丽
卢强
王鹏
陶伟
陈明
马涛
王鹏
(2)三(1)班喜欢篮球的有( )人;喜欢足球的有( )人;既喜欢篮球又喜欢足球的有( )人。
8
9
4
3.下面三(1)班同学喜欢球类运动的情况。
喜欢篮球
喜欢足球
陈明
张旭
刘东
刘红
李平
赵霞
张伟
刘东
苏军
李丽
李丽
卢强
王鹏
陶伟
陈明
马涛
王鹏
(3)三(1)班喜欢球类运动的一共 多少人?
8 + 9 – 4 = 13(人)
13
教材第105页思考题
4.学校举行乒乓球比赛,A组、B组两个小组各有16人,每组两人一对进行比赛,负者被淘汰,胜者进入下一轮,最后两组第一名进行决赛。两个小组赛一共要进行多少场比赛?
提示:求两个小组赛一共参加比赛的场次,即要求出A、B两组的比赛场次,不加上决赛。
教材第105页思考题
8+4+2+1=15(场)
15 + 15 = 30(场)
答:两个小组赛一共要进行30场比赛。
4.学校举行乒乓球比赛,A组、B组两个小组各有16人,每组两人一对进行比赛,负者被淘汰,胜者进入下一轮,最后两组第一名进行决赛。两个小组赛一共要进行多少场比赛?
方法一
A或B参加比赛的场次
16÷2=8(场)
8÷2=4(场)
4÷2=2(场)
教材第105页思考题
15 + 15 = 30(场)
答:两个小组赛一共要进行30场比赛。
4.学校举行乒乓球比赛,A组、B组两个小组各有16人,每组两人一对进行比赛,负者被淘汰,胜者进入下一轮,最后两组第一名进行决赛。两个小组赛一共要进行多少场比赛?
方法二
要想淘汰一人
进行一场比赛
每组要淘汰15人
每组进行15场比赛
02
01
课堂小结
重叠问题的解题方法
只参加A的
只参加B的
A和B
总数= 只参加A的+只参加B的+A和B都参加的
总数= 参加A的+参加B的-A和B都参加的
相关练习。
02
01
课后练习第1题。
课后作业
人教版数学三年级(上)
数学广角——集合
9
1.经历解决问题的过程,了解简单的集合知识,初步感受它的意义。
2.学会借助维恩图,利用集合的思想方法来解决较简单的实际问题,从而感受数学与生活之间的相互关系。
3.培养乐于观察,合作学习的意识和学习的兴趣。
学习目标
【重点】
理解集合的意义,了解维恩图。
【难点】
能利用集合思想解决问题。
课堂导入
脑筋急转弯。
两位妈妈和两个女儿一同去看电影(每人都得买一张票),可是她们只买了3张票,便顺利地进了电影院。这是为什么?
姥姥
妈妈
女儿
妈妈
女儿
探究新知
下面是三(1)班参加跳绳、踢毽的学生名单。
参加这两项比赛的共有多少人?
跳绳
踢毽
杨明
陈东
刘红
李芳
王爱华
马超
丁旭
赵军
徐强
杨明
刘红
于丽
周晓
朱小东
陶伟
李芳
卢强
1
跳绳的有9人,踢毽的有8人。
跳绳
踢毽
杨明
陈东
刘红
李芳
王爱华
马超
丁旭
赵军
徐强
杨明
刘红
于丽
周晓
朱小东
陶伟
李芳
卢强
一共有17人。
可是参加这两项比赛的没有17人呀?
我发现有的人两项比赛都参加了。
跳绳
踢毽
杨明
陈东
刘红
李芳
王爱华
马超
丁旭
赵军
徐强
杨明
刘红
于丽
周晓
朱小东
陶伟
李芳
卢强
怎样表示能清楚地看出来呢?
我把两项比赛都参加的人连起来,有3个重复的。
跳绳
踢毽
杨明
陈东
刘红
李芳
王爱华
马超
丁旭
赵军
徐强
杨明
刘红
于丽
周晓
朱小东
陶伟
李芳
卢强
用图表示就清楚了
跳绳
踢毽
杨明
陈东
刘红
李芳
王爱华
马超
丁旭
赵军
徐强
杨明
刘红
于丽
周晓
朱小东
陶伟
李芳
卢强
两项都参加的学生
只参加跳绳的学生
只参加踢毽的学生
跳绳的学生
踢毽的学生
跳绳
踢毽
杨明
陈东
刘红
李芳
王爱华
马超
丁旭
赵军
徐强
杨明
刘红
于丽
周晓
朱小东
陶伟
李芳
卢强
两项都参加的学生
跳绳的学生
踢毽的学生
把指定的具有某种性质的事物看作一个整体,这个整体就是一个集合。
想一想,可以怎样列式解答?
在数学中,我们经常用平面上封闭曲线的内部代表集合,这种图称为维恩图。
跳绳总人数+踢毽总人数–两项都参加人数
9 + 8 – 3 = 14(人)
1.从图形整体观察:
只参加跳绳人数+踢毽总人数
9 – 3 + 8 = 14(人)
2.从图形左侧入手观察:
8 – 3 + 9 = 14(人)
只参加踢毽人数+跳绳总人数
3.从图形右侧入手观察:
两项都参加人数 + 只参加跳绳人数 + 只参加踢毽人数
4.从图形中心入手观察:
3 +(9 – 3)+(8 – 3)= 14(人)
答:参加比赛的共有14人。
参加这两项比赛的共有多少人?
9 + 8 – 3 = 14(人)
3 +(9 – 3)+(8 – 3)= 14(人)
9 – 3 + 8 = 14(人)
8 – 3 + 9 = 14(人)
课堂练习
教材第105页“做一做”
1.把下面动物的序号填写在合适的圈里。
会游泳的
会飞的
表示什么?
做一做
①
②
③
④
⑤
⑥
⑦
⑧
⑨
⑩
教材第105页“做一做”
会游泳的
会飞的
表示什么?
①
②
③
④
⑤
⑥
⑦
⑧
⑨
⑩
既会游泳又会飞的
2.
(1)既荣获“语文之星”又荣获“数学之星”的
有( )人。
6
做一做
2.
(2)上光荣榜的一共有( )人。
19
做一做
13 + 12 – 6 = 19(人)
3.下面三(1)班同学喜欢球类运动的情况。
喜欢篮球
喜欢足球
喜欢篮球
喜欢足球
既喜欢篮球又喜欢足球
(1)把图补充完整。
陈明
张旭
刘东
刘红
李平
赵霞
张伟
刘东
苏军
李丽
李丽
卢强
王鹏
陶伟
陈明
马涛
王鹏
3.下面三(1)班同学喜欢球类运动的情况。
喜欢篮球
喜欢足球
陈明
张旭
刘东
刘红
李平
赵霞
张伟
刘东
苏军
李丽
李丽
卢强
王鹏
陶伟
陈明
马涛
王鹏
(2)三(1)班喜欢篮球的有( )人;喜欢足球的有( )人;既喜欢篮球又喜欢足球的有( )人。
8
9
4
3.下面三(1)班同学喜欢球类运动的情况。
喜欢篮球
喜欢足球
陈明
张旭
刘东
刘红
李平
赵霞
张伟
刘东
苏军
李丽
李丽
卢强
王鹏
陶伟
陈明
马涛
王鹏
(3)三(1)班喜欢球类运动的一共 多少人?
8 + 9 – 4 = 13(人)
13
教材第105页思考题
4.学校举行乒乓球比赛,A组、B组两个小组各有16人,每组两人一对进行比赛,负者被淘汰,胜者进入下一轮,最后两组第一名进行决赛。两个小组赛一共要进行多少场比赛?
提示:求两个小组赛一共参加比赛的场次,即要求出A、B两组的比赛场次,不加上决赛。
教材第105页思考题
8+4+2+1=15(场)
15 + 15 = 30(场)
答:两个小组赛一共要进行30场比赛。
4.学校举行乒乓球比赛,A组、B组两个小组各有16人,每组两人一对进行比赛,负者被淘汰,胜者进入下一轮,最后两组第一名进行决赛。两个小组赛一共要进行多少场比赛?
方法一
A或B参加比赛的场次
16÷2=8(场)
8÷2=4(场)
4÷2=2(场)
教材第105页思考题
15 + 15 = 30(场)
答:两个小组赛一共要进行30场比赛。
4.学校举行乒乓球比赛,A组、B组两个小组各有16人,每组两人一对进行比赛,负者被淘汰,胜者进入下一轮,最后两组第一名进行决赛。两个小组赛一共要进行多少场比赛?
方法二
要想淘汰一人
进行一场比赛
每组要淘汰15人
每组进行15场比赛
02
01
课堂小结
重叠问题的解题方法
只参加A的
只参加B的
A和B
总数= 只参加A的+只参加B的+A和B都参加的
总数= 参加A的+参加B的-A和B都参加的
相关练习。
02
01
课后练习第1题。
课后作业
