山东省淄博市高青县2020-2021学年第二学期(五四学制)六年级数学期末试题(word版,含答案)
文档属性
| 名称 | 山东省淄博市高青县2020-2021学年第二学期(五四学制)六年级数学期末试题(word版,含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 277.2KB | ||
| 资源类型 | 素材 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-15 00:00:00 | ||
图片预览




文档简介
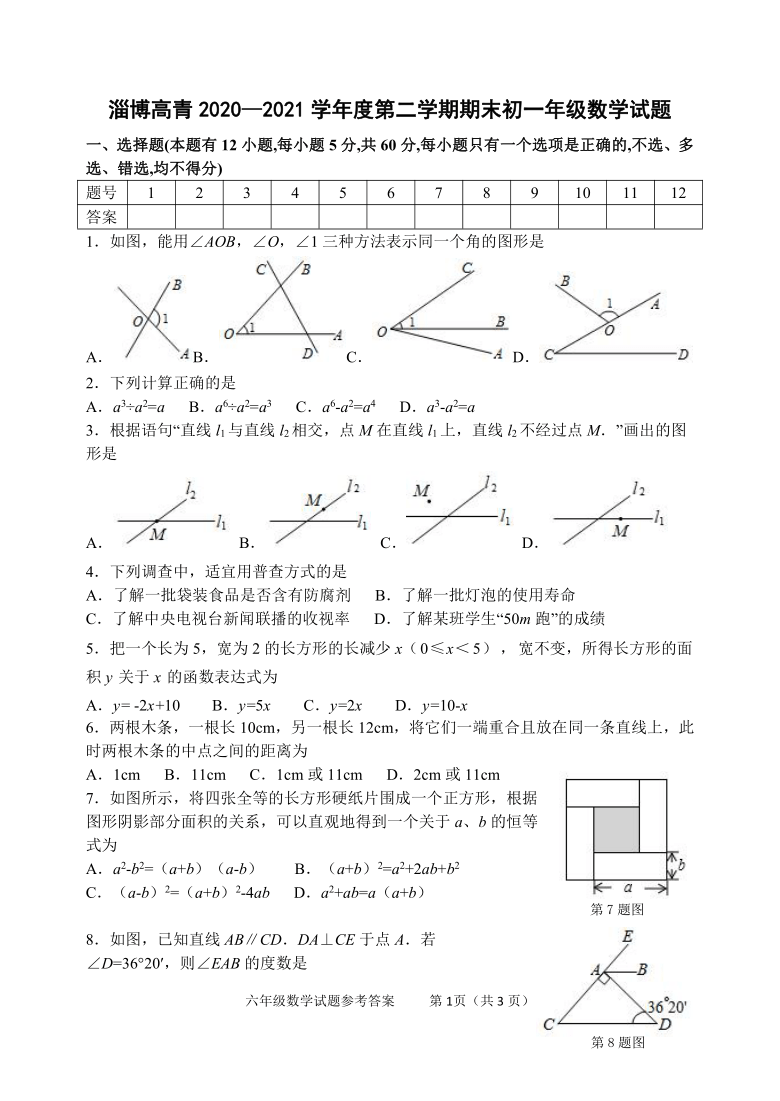
淄博高青2020—2021学年度第二学期期末初一年级数学试题
一、选择题(本题有12小题,每小题5分,共60分,每小题只有一个选项是正确的,不选、多选、错选,均不得分)
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
1.如图,能用∠AOB,∠O,∠1三种方法表示同一个角的图形是
A.B.C.D.
2.下列计算正确的是
A.a3÷a2=a
B.a6÷a2=a3
C.a6-a2=a4
D.a3-a2=a
3.根据语句“直线l1与直线l2相交,点M在直线l1上,直线l2不经过点M.”画出的图形是
A.
B.
C.
D.
4.下列调查中,适宜用普查方式的是
A.了解一批袋装食品是否含有防腐剂
B.了解一批灯泡的使用寿命
C.了解中央电视台新闻联播的收视率
D.了解某班学生“50m跑”的成绩
5.把一个长为5,宽为2的长方形的长减少x(0≤x<5),宽不变,所得长方形的面积y关于x的函数表达式为
A.y=
-2x+10
B.y=5x
C.y=2x
D.y=10-x
6.两根木条,一根长10cm,另一根长12cm,将它们一端重合且放在同一条直线上,此时两根木条的中点之间的距离为
A.1cm
B.11cm
C.1cm?或11cm
D.2cm或11cm
7.如图所示,将四张全等的长方形硬纸片围成一个正方形,根据图形阴影部分面积的关系,可以直观地得到一个关于a、b的恒等式为
A.a2-b2=(a+b)(a-b)
B.(a+b)2=a2+2ab+b2
C.(a-b)2=(a+b)2-4ab
D.a2+ab=a(a+b)
8.如图,已知直线AB∥CD.DA⊥CE于点A.若
∠D=36°20′,则∠EAB的度数是
A.63°40′
B.53°40′
C.44°40′
D.36°20′
9.某学校为了加强学生的安全意识,组织学生观看了纪实片《孩子,请不要私自下水》,并对部分学生进行调查.根据下面两幅不完整的统计图可以求出,在这次调查中被调查的学生有
A.400名
B.380名
C.350名
D.300名
10.为了建设社会主义新农村,我市积极推进“行政村通畅工程”,对甲村和乙村之间的道路需要进行改造,施工队在工作了一段时间后,因暴雨被迫停工几天,不过施工队随后加快了施工进度,按时完成了两村之间道路的改造,下面能反映该工程改造道路里程y(公里)与时间x(天)的函数关系大致的图象是
A.
B.C.D.
11.有一个长方形内部剪掉了一个小长方形,它们的尺寸如图所示,则余下的部分(阴影部分)的面积
A.4a2
B.4a2-ab-2b2
C.4a2+ab
D.
4a2-ab
12.在同一平面内,若∠A与∠B的两边分别平行,且∠A比∠B的3倍少40°,则∠A的度数为
A.20°
B.55°
C.20°或125°
D.20°或55°
二、填空题(共5小题,每小题4分,满分20分)
13.如图,点O在直线AE上,射线OC平分∠AOE.如果∠DOB=90°,∠1=25°,那么∠AOB的度数为
°.
第13题图
第17题图
14.已知10a=2,10b=3,则102a+3b=
.
15.小鸡孵化场孵化出一批小鸡,工人在其中50只小鸡上做记号后让这批小鸡充分跑散,后来再任意抓出100只小鸡,其中有记号的有10只,则这批小鸡大约有
只.
16.某市出租车白天的收费起步价为7元,即路程不超过3千米时收费7元,超过部分每千米收费1.2元,如果乘客白天乘坐出租车的路程为x(x>3)千米,乘车费为y元,那么y与x之间的关系为
.
17.如图,已知AB∥CD,则∠A、∠C、∠P的数量关系为
.
三、解答题(共7小题,共70分)
18.化简:
(1)2(2x2-xy)+x(x-y);
(2)ab(2ab2-a2b)-(2ab)2b+a3b2.
19.如图,点B是线段AC上一点,且AB=21cm,BC=AB.
(1)试求出线段AC的长;
(2)如果点O是线段AC的中点,请求线段OB的长.
20.某校进行“垃圾分一分,环境美十分”的主题宣传活动,随机调查了部分学生对垃圾分类知识的了解情况.调查选项分为“A:非常了解,B:比较了解,C:基本了解,D:不了解”四种,并将调查结果绘制成如图两幅不完整的统计图.
请根据图中提供的信息,解答下列问题:
(1)把两幅统计图补充完整;
(2)本次调查了
名学生;
(3)根据上述调查数据,请你提出一条合理化建议
.
21.“珍重生命,注意安全!”同学们在上下学途中一定要注意骑车安全.小明骑单车上学,当他骑了一段时,想起要买某本书,于是又折回到刚经过的新华书店,买到书后继续去学校,以下是他本次行程离家距离与所用的时间的关系示意图.根据图中提供的信息回答下列问题:
(1)小明家到学校的路程是多少米?
(2)小明在书店停留了多少分钟?
(3)本次从家到学校的整个过程中,小明一共行驶了多少米?一共用了多少分钟?
(4)我们认为骑单车的速度超过300米/分钟就超越了安全限度.问:在整个上学的途中哪个时间段小明骑车速度最快,速度在安全限度内吗?
22.如图,AC∥FE,∠1+∠3=180°.
(1)判定∠FAB与∠4的大小关系,并说明理由;
(2)若AC平分∠FAB,EF⊥BE于点E,∠4=78°,求∠BCD的度数.
23.如图1,将一个长为4a,宽为2b的长方形,沿图中虚线均匀分成4个小长方形,然后按图2形状拼成一个正方形.
(1)图2的空白部分的边长是多少?(用含a、b的式子表示)
(2)若2a+b=7,且ab=3,求图2中的空白正方形的面积.
(3)观察图2,用等式表示出(2a-b)2,ab和(2a+b)2的数量关系.
24.如图,AB∥CD,∠ABE=120°.
(1)如图①,写出∠BED与∠D的数量关系,并证明你的结论;
(2)如图②,∠DEF=2∠BEF,∠CDF=∠CDE,EF与DF交于点F,求∠EFD的度数;
(3)如图③,过B作BG⊥AB于G点,∠CDE=4∠GDE,求的值.
2020——2021学年度第二学期期末考试
六年级数学参考答案
一、选择题:本题共12小题,每小题5分,共60分
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
B
A
D
D
A
C
C
B
A
B
D
C
二、填空题:每小题4分,共20分
题号
13
14
15
16
17
答案
25
108
500
y=1.2x+3.4
∠A+∠C-∠P=180°
三、解答题:
18.解:(1)2(2x2-xy)+x(x-y)=4x2-2xy+x2-xy=5x2-3xy;………………………4分
(2)ab(2ab2-a2b)-(2ab)2b+a3b2=2a2b3-a3b2-4a2b3+a3b2=-2a2b3.………………8分
19.解:(1)∵AB=21cm,BC=AB=7cm,
∴AC=AB+BC=21+7=28(cm);…………………………………………4分
(2)由(1)知:AC=28cm,
∵点O是线段AC的中点,
∴CO=AC=×28=14(cm),
∴OB=CO-BC=14-7=7(cm).……………………………………………8分
20.解:(1)5÷10%=50(人),25÷50=50%,50×26%=13(人),50-5-25-13=7(人),7÷50=14%,补全的统计图如图所示:
……………………4分
(2)5÷10%=50(人);…………………………………………………………………7分
(3)根据对垃圾分类知识的了解情况,各占的百分比,对于“非常了解”的占比较小(或仍有14%的同学不了解),需要进一步加强宣传的力度.……………………10分
21.解:(1)根据图象,小明家到学校的路程是1500米;……………………2分
(2)根据题意,小明在书店停留的时间为从(8分)到(12分),
故小明在书店停留了4分钟.………………………………………………………4分
(3)一共行驶的总路程=1200+(1200-600)+(1500-600)
=1200+600+900=2700米;共用了14分钟.………………………………………7分
(4)由图象可知:0~6分钟时,平均速度==200米/分,
6~8分钟时,平均速度==300米/分,
12~14分钟时,平均速度==450米/分,
所以,12~14分钟时速度最快,不在安全限度内.……………………………10分
22.解:(1)∠FAB=∠4,
理由如下:∵AC∥EF,∴∠1+∠2=180°,
又∵∠1+∠3=180°,∴∠2=∠3,∴FA∥CD,∴∠FAB=∠4;………………5分
(2)∵AC平分∠FAB,∴∠2=∠CAD,
∵∠2=∠3,∴∠CAD=∠3,
∵∠4=∠3+∠CAD,∴∠3=∠4=×78°=39°,
∵EF⊥BE,AC∥EF,∴AC⊥BE,∴∠ACB=90°,
∴∠BCD=90°-∠3=51°.…………………………………………………………10分
23.解:(1)图2的空白部分的边长是2a-b…………………………4分
(2)由图21-2可知,小正方形的面积=大正方形的面积-4个小长方形的面积,
∵大正方形的边长=2a+b=7,∴大正方形的面积=(2a+b)2=49,
又∵4个小长方形的面积之和=大长方形的面积=4a×2b=8ab=8×3=24,
∴小正方形的面积=(2a-b)2=49-24=25………………………………8分
(3)由图2可以看出,大正方形面积=空白部分的正方形的面积+四个小长方形的面积
即:(2a+b)2-(2a-b)2=8ab.…………………………………………12分
24.解:(1)结论:∠BED+∠D=120°,
证明:如图①,延长AB交DE于点F,
∵AB∥CD,∴∠BFE=∠D,
∵∠ABE=120°,∴∠BFE+∠BED=∠ABE=120°,
∴∠D+∠BED=120°;……………………4分
(2)如图②,
∵∠DEF=2∠BEF,∠CDF=∠CDE,
即∠CDE=3∠CDF,
设∠BEF=α,∠CDF=β,
∴∠DEF=2α,∠DEB=3α,∠CDE=3β,∠EDF=2β,
由(1)知:∠BED+∠CDE=120°,
∴3α+3β=120°,
∴α+β=40°,
∴2α+2β=80°,
∴∠EFD=180°-∠DEF-∠EDF=180°-(2α+2β)=180°-80°=100°,
答:∠EFD的度数为100°;…………………………8分
(3)如图③,∵BG⊥AB,∴∠ABG=90°,
∵∠ABE=120°.∴∠GBE=∠ABE-∠ABG=30°,
∵∠CDE=4∠GDE,∴∠GDE=∠CDE,
∵∠G+∠GBE=∠E+∠GDE,∴∠G+30°=∠E+∠CDE,
由(1)知:∠BED+∠CDE=120°,
∴∠CDE=120°-∠E,
∴∠G+30°=∠E+(120°-∠E),
∴∠G=∠E,
∴=.…………………………………………12分
六年级数学试题参考答案
第7页(共3页)
一、选择题(本题有12小题,每小题5分,共60分,每小题只有一个选项是正确的,不选、多选、错选,均不得分)
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
1.如图,能用∠AOB,∠O,∠1三种方法表示同一个角的图形是
A.B.C.D.
2.下列计算正确的是
A.a3÷a2=a
B.a6÷a2=a3
C.a6-a2=a4
D.a3-a2=a
3.根据语句“直线l1与直线l2相交,点M在直线l1上,直线l2不经过点M.”画出的图形是
A.
B.
C.
D.
4.下列调查中,适宜用普查方式的是
A.了解一批袋装食品是否含有防腐剂
B.了解一批灯泡的使用寿命
C.了解中央电视台新闻联播的收视率
D.了解某班学生“50m跑”的成绩
5.把一个长为5,宽为2的长方形的长减少x(0≤x<5),宽不变,所得长方形的面积y关于x的函数表达式为
A.y=
-2x+10
B.y=5x
C.y=2x
D.y=10-x
6.两根木条,一根长10cm,另一根长12cm,将它们一端重合且放在同一条直线上,此时两根木条的中点之间的距离为
A.1cm
B.11cm
C.1cm?或11cm
D.2cm或11cm
7.如图所示,将四张全等的长方形硬纸片围成一个正方形,根据图形阴影部分面积的关系,可以直观地得到一个关于a、b的恒等式为
A.a2-b2=(a+b)(a-b)
B.(a+b)2=a2+2ab+b2
C.(a-b)2=(a+b)2-4ab
D.a2+ab=a(a+b)
8.如图,已知直线AB∥CD.DA⊥CE于点A.若
∠D=36°20′,则∠EAB的度数是
A.63°40′
B.53°40′
C.44°40′
D.36°20′
9.某学校为了加强学生的安全意识,组织学生观看了纪实片《孩子,请不要私自下水》,并对部分学生进行调查.根据下面两幅不完整的统计图可以求出,在这次调查中被调查的学生有
A.400名
B.380名
C.350名
D.300名
10.为了建设社会主义新农村,我市积极推进“行政村通畅工程”,对甲村和乙村之间的道路需要进行改造,施工队在工作了一段时间后,因暴雨被迫停工几天,不过施工队随后加快了施工进度,按时完成了两村之间道路的改造,下面能反映该工程改造道路里程y(公里)与时间x(天)的函数关系大致的图象是
A.
B.C.D.
11.有一个长方形内部剪掉了一个小长方形,它们的尺寸如图所示,则余下的部分(阴影部分)的面积
A.4a2
B.4a2-ab-2b2
C.4a2+ab
D.
4a2-ab
12.在同一平面内,若∠A与∠B的两边分别平行,且∠A比∠B的3倍少40°,则∠A的度数为
A.20°
B.55°
C.20°或125°
D.20°或55°
二、填空题(共5小题,每小题4分,满分20分)
13.如图,点O在直线AE上,射线OC平分∠AOE.如果∠DOB=90°,∠1=25°,那么∠AOB的度数为
°.
第13题图
第17题图
14.已知10a=2,10b=3,则102a+3b=
.
15.小鸡孵化场孵化出一批小鸡,工人在其中50只小鸡上做记号后让这批小鸡充分跑散,后来再任意抓出100只小鸡,其中有记号的有10只,则这批小鸡大约有
只.
16.某市出租车白天的收费起步价为7元,即路程不超过3千米时收费7元,超过部分每千米收费1.2元,如果乘客白天乘坐出租车的路程为x(x>3)千米,乘车费为y元,那么y与x之间的关系为
.
17.如图,已知AB∥CD,则∠A、∠C、∠P的数量关系为
.
三、解答题(共7小题,共70分)
18.化简:
(1)2(2x2-xy)+x(x-y);
(2)ab(2ab2-a2b)-(2ab)2b+a3b2.
19.如图,点B是线段AC上一点,且AB=21cm,BC=AB.
(1)试求出线段AC的长;
(2)如果点O是线段AC的中点,请求线段OB的长.
20.某校进行“垃圾分一分,环境美十分”的主题宣传活动,随机调查了部分学生对垃圾分类知识的了解情况.调查选项分为“A:非常了解,B:比较了解,C:基本了解,D:不了解”四种,并将调查结果绘制成如图两幅不完整的统计图.
请根据图中提供的信息,解答下列问题:
(1)把两幅统计图补充完整;
(2)本次调查了
名学生;
(3)根据上述调查数据,请你提出一条合理化建议
.
21.“珍重生命,注意安全!”同学们在上下学途中一定要注意骑车安全.小明骑单车上学,当他骑了一段时,想起要买某本书,于是又折回到刚经过的新华书店,买到书后继续去学校,以下是他本次行程离家距离与所用的时间的关系示意图.根据图中提供的信息回答下列问题:
(1)小明家到学校的路程是多少米?
(2)小明在书店停留了多少分钟?
(3)本次从家到学校的整个过程中,小明一共行驶了多少米?一共用了多少分钟?
(4)我们认为骑单车的速度超过300米/分钟就超越了安全限度.问:在整个上学的途中哪个时间段小明骑车速度最快,速度在安全限度内吗?
22.如图,AC∥FE,∠1+∠3=180°.
(1)判定∠FAB与∠4的大小关系,并说明理由;
(2)若AC平分∠FAB,EF⊥BE于点E,∠4=78°,求∠BCD的度数.
23.如图1,将一个长为4a,宽为2b的长方形,沿图中虚线均匀分成4个小长方形,然后按图2形状拼成一个正方形.
(1)图2的空白部分的边长是多少?(用含a、b的式子表示)
(2)若2a+b=7,且ab=3,求图2中的空白正方形的面积.
(3)观察图2,用等式表示出(2a-b)2,ab和(2a+b)2的数量关系.
24.如图,AB∥CD,∠ABE=120°.
(1)如图①,写出∠BED与∠D的数量关系,并证明你的结论;
(2)如图②,∠DEF=2∠BEF,∠CDF=∠CDE,EF与DF交于点F,求∠EFD的度数;
(3)如图③,过B作BG⊥AB于G点,∠CDE=4∠GDE,求的值.
2020——2021学年度第二学期期末考试
六年级数学参考答案
一、选择题:本题共12小题,每小题5分,共60分
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
B
A
D
D
A
C
C
B
A
B
D
C
二、填空题:每小题4分,共20分
题号
13
14
15
16
17
答案
25
108
500
y=1.2x+3.4
∠A+∠C-∠P=180°
三、解答题:
18.解:(1)2(2x2-xy)+x(x-y)=4x2-2xy+x2-xy=5x2-3xy;………………………4分
(2)ab(2ab2-a2b)-(2ab)2b+a3b2=2a2b3-a3b2-4a2b3+a3b2=-2a2b3.………………8分
19.解:(1)∵AB=21cm,BC=AB=7cm,
∴AC=AB+BC=21+7=28(cm);…………………………………………4分
(2)由(1)知:AC=28cm,
∵点O是线段AC的中点,
∴CO=AC=×28=14(cm),
∴OB=CO-BC=14-7=7(cm).……………………………………………8分
20.解:(1)5÷10%=50(人),25÷50=50%,50×26%=13(人),50-5-25-13=7(人),7÷50=14%,补全的统计图如图所示:
……………………4分
(2)5÷10%=50(人);…………………………………………………………………7分
(3)根据对垃圾分类知识的了解情况,各占的百分比,对于“非常了解”的占比较小(或仍有14%的同学不了解),需要进一步加强宣传的力度.……………………10分
21.解:(1)根据图象,小明家到学校的路程是1500米;……………………2分
(2)根据题意,小明在书店停留的时间为从(8分)到(12分),
故小明在书店停留了4分钟.………………………………………………………4分
(3)一共行驶的总路程=1200+(1200-600)+(1500-600)
=1200+600+900=2700米;共用了14分钟.………………………………………7分
(4)由图象可知:0~6分钟时,平均速度==200米/分,
6~8分钟时,平均速度==300米/分,
12~14分钟时,平均速度==450米/分,
所以,12~14分钟时速度最快,不在安全限度内.……………………………10分
22.解:(1)∠FAB=∠4,
理由如下:∵AC∥EF,∴∠1+∠2=180°,
又∵∠1+∠3=180°,∴∠2=∠3,∴FA∥CD,∴∠FAB=∠4;………………5分
(2)∵AC平分∠FAB,∴∠2=∠CAD,
∵∠2=∠3,∴∠CAD=∠3,
∵∠4=∠3+∠CAD,∴∠3=∠4=×78°=39°,
∵EF⊥BE,AC∥EF,∴AC⊥BE,∴∠ACB=90°,
∴∠BCD=90°-∠3=51°.…………………………………………………………10分
23.解:(1)图2的空白部分的边长是2a-b…………………………4分
(2)由图21-2可知,小正方形的面积=大正方形的面积-4个小长方形的面积,
∵大正方形的边长=2a+b=7,∴大正方形的面积=(2a+b)2=49,
又∵4个小长方形的面积之和=大长方形的面积=4a×2b=8ab=8×3=24,
∴小正方形的面积=(2a-b)2=49-24=25………………………………8分
(3)由图2可以看出,大正方形面积=空白部分的正方形的面积+四个小长方形的面积
即:(2a+b)2-(2a-b)2=8ab.…………………………………………12分
24.解:(1)结论:∠BED+∠D=120°,
证明:如图①,延长AB交DE于点F,
∵AB∥CD,∴∠BFE=∠D,
∵∠ABE=120°,∴∠BFE+∠BED=∠ABE=120°,
∴∠D+∠BED=120°;……………………4分
(2)如图②,
∵∠DEF=2∠BEF,∠CDF=∠CDE,
即∠CDE=3∠CDF,
设∠BEF=α,∠CDF=β,
∴∠DEF=2α,∠DEB=3α,∠CDE=3β,∠EDF=2β,
由(1)知:∠BED+∠CDE=120°,
∴3α+3β=120°,
∴α+β=40°,
∴2α+2β=80°,
∴∠EFD=180°-∠DEF-∠EDF=180°-(2α+2β)=180°-80°=100°,
答:∠EFD的度数为100°;…………………………8分
(3)如图③,∵BG⊥AB,∴∠ABG=90°,
∵∠ABE=120°.∴∠GBE=∠ABE-∠ABG=30°,
∵∠CDE=4∠GDE,∴∠GDE=∠CDE,
∵∠G+∠GBE=∠E+∠GDE,∴∠G+30°=∠E+∠CDE,
由(1)知:∠BED+∠CDE=120°,
∴∠CDE=120°-∠E,
∴∠G+30°=∠E+(120°-∠E),
∴∠G=∠E,
∴=.…………………………………………12分
六年级数学试题参考答案
第7页(共3页)
同课章节目录
