山东省淄博市高青县2020-2021学年第二学期(五四学制)七年级数学期末试题(word版,含答案)
文档属性
| 名称 | 山东省淄博市高青县2020-2021学年第二学期(五四学制)七年级数学期末试题(word版,含答案) | 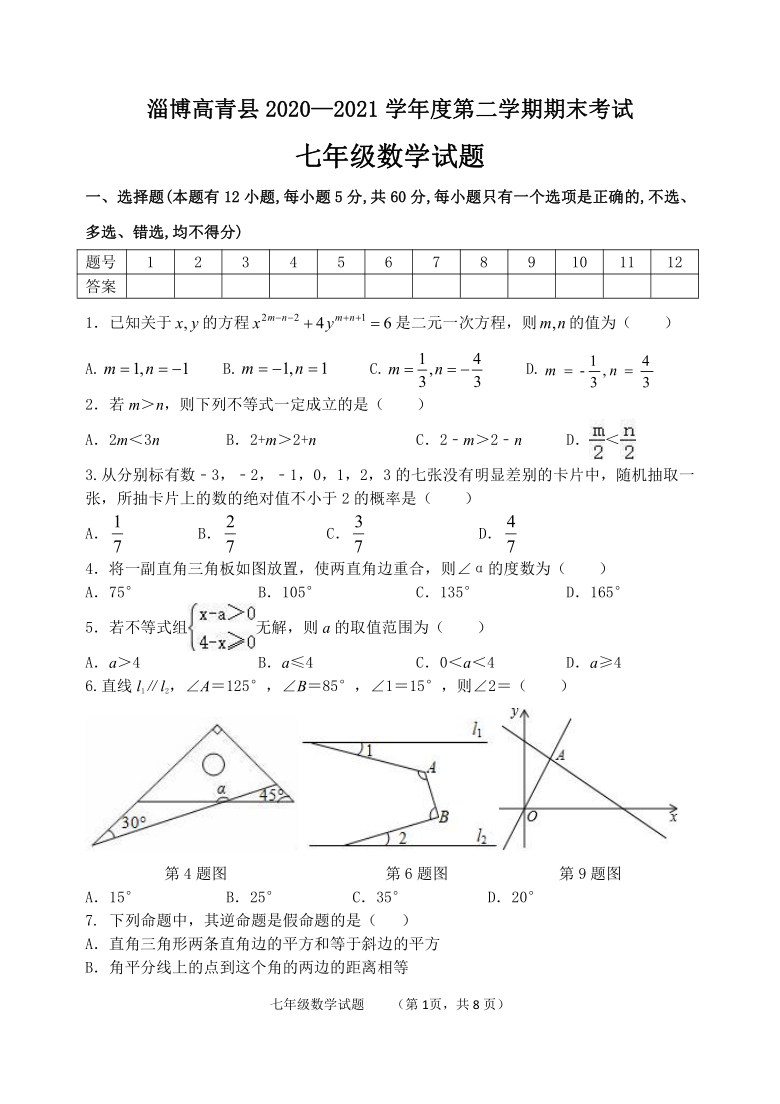 | |
| 格式 | zip | ||
| 文件大小 | 215.1KB | ||
| 资源类型 | 素材 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-15 17:23:06 | ||
图片预览





文档简介
淄博高青县2020—2021学年度第二学期期末考试
七年级数学试题
一、选择题(本题有12小题,每小题5分,共60分,每小题只有一个选项是正确的,不选、多选、错选,均不得分)
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
1.已知关于的方程是二元一次方程,则的值为(
)
A.
B.
C.
D.
2.若m>n,则下列不等式一定成立的是( )
A.2m<3n
B.2+m>2+n
C.2﹣m>2﹣n
D.<
3.从分别标有数﹣3,﹣2,﹣1,0,1,2,3的七张没有明显差别的卡片中,随机抽取一张,所抽卡片上的数的绝对值不小于2的概率是( )
A.
B.
C.
D.
4.将一副直角三角板如图放置,使两直角边重合,则∠α的度数为( )
A.75°
B.105°
C.135°
D.165°
5.若不等式组无解,则a的取值范围为( )
A.a>4
B.a≤4
C.0<a<4
D.a≥4
6.直线l1∥l2,∠A=125°,∠B=85°,∠1=15°,则∠2=( )
第4题图
第6题图
第9题图
A.15°
B.25°
C.35°
D.20°
7.
下列命题中,其逆命题是假命题的是(
)
A.直角三角形两条直角边的平方和等于斜边的平方
B.角平分线上的点到这个角的两边的距离相等
C.如果a3=b3,那么a2=b2
D.两直线平行,内错角相等
8.
两位同学在解方程组时,甲同学由正确地解出,乙同学因把c写错了解得,则a+b+c的值为( )
A.3
B.0
C.1
D.7
9.如图,函数y=2x和y=ax+4的图象相交于点A(m,3),则不等式2x≤ax+4的解集为
A.
x≤3
B.
x≥3
C.
x≤
D.
x≥
10.如图,在Rt△ABC中,∠C=90°,BE平分∠ABC,ED垂直平分AB于D,若AC=9,则AE的值是( )
A.3
B.5
C.6
D.4
11.如图,已知GF⊥AB,∠1=∠2,∠B=∠AGH,则下列结论中:①GH∥BC;②∠D=∠F;③HE平分∠AHG;④HE⊥AB,其中正确的有( )
A.0个
B.1个
C.2个
D.3个
第10题图
第11题图
第12题图
12.
如图,AD是△ABC的角平分线,DF⊥AB于点F,且DE=DG,S△ADG=24,S△AED=18,则△DEF的面积为( )
A.2
B.3
C.4
D.6
二、填空题(共5小题,每小题4分,满分20分)
13.已知关于x的不等式组的整数解共有5个,则a的取值范围是
.
14.若方程组的解也是二元一次方程x﹣y=1的一个解,则a=
.
15.如图,“赵爽弦图”是吴国的赵爽创制的.以直角三角形的斜边为边长得到一个正方形,该正方形由4个全等的直角三角形再加上中间的小正方形组成,在一次游园活动中,数学小组制作了一面“赵爽弦图锣”,其中∠ABC=90°,AC=13cm,AB=5cm,小明蒙上眼睛用棍子击中了锣面,他击中阴影部分的概率是
.
16.如图,将一条对边互相平行的纸带进行两次折叠,折痕分别为AB,CD.若CD∥BE,∠1=28°,则∠2的度数是
.
第15题图
第16题图
第17题图
17.如图,已知△ABC中,AB=AC,AD是BC边上的中线,且∠BAD=40°.点E是边AC上的一点,若△ADE为等腰三角形,则∠EDC的度数是
.
三、解答题(共7小题,共70分)
18.
解下列方程组
(1)
(2)
19.
(1)解不等式组,并把解集在数轴上表示出来.
(2)求不等式组的整数解
20.
如图,AD∥EF,∠1+∠2=180°.
(1)若∠1=50°,求∠BAD的度数;
(2)若DG⊥AC,垂足为G,∠BAC=90°,试说明:DG平分∠ADC.
21.一个不透明的袋中装有红、黄、白三种颜色球共100个,它们除颜色外其他都相同,其中黄球个数是白球个数的2倍少5个.已知从袋中摸出一个球是红球的概率是.
(1)求袋中红球的个数;
(2)求从袋中摸出一个球是白球的概率;
(3)取走10个球(其中没有红球)后,求从剩余的球中摸出一个球是红球的概率.
22.为了美化校园,我校欲购进甲、乙两种工具,如果购买甲种3件,乙种2件,共需56元;如果购买甲种1件,乙种4件,共需32元.
(1)甲、乙两种工具每件各多少元?
(2)现要购买甲、乙两种工具共100件,总费用不超过1000元,那么甲种工具最多购买多少件?
23.如图,△ABC和△EBD中,∠ABC=∠DBE=90°,AB=CB,BE=BD,连接AE,CD,AE与CD交于点M,AE与BC交于点N.
(1)求证:AE=CD;
(2)求证:AE⊥CD;
(3)求证:MB平分∠AMD.
24.已知,在△ABC中,∠ABC=∠ACB,点D为射线CB上一点,过点D作DE⊥AC于点E.
(1)如图1,当点D在线段BC上时,请直接写出∠BAC与∠EDC的数量关系:
.
(2)如图2,当点D在CB的延长线上时,画出图形,探究∠BAC与∠EDC的数量关系,并说明理由.
(3)在(2)的条件下,点F为线段BC上一点,过点F作FG⊥AC于点G,连接AF,且∠AFG=∠CFG,∠BAF=∠BFA,延长ED、AB交于点K,求∠EKA的度数.
参考答案
一、选择题:本题共12小题,每小题5分,共60分
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
A
B
D
D
D
A
C
D
C
C
C
B
二、填空题:每小题4分,共20分。
13.
﹣3<a≤﹣2
14.
15.
16.56°
17.50°或20°
三、解答题:
18.(每小题4分,共8分)
解:(1)
原方程组的解是.……………………………………………………………4分
(2)
原方程组的解是.…………………………………………………………4分
19.(每小题4分,共8分)
(1)由(1)得:
由(2)得:
…………………3分
……………………………………………………………1分
(2)化简得
整理得:-1≤x<3.
…………………………………………………………………………3分
原不等式组的整数解为:x=-1,0,1,2.
………………………………………………1分
20.
(1)解:∵AD∥EF,
∴∠BAD+∠2=180°,
∵∠1+∠2=180°,
∴∠1=∠BAD,
∵∠1=50°,
∴∠BAD=50°;………………………………………………………………………5分
(2)证明:∵DG⊥AC,
∴∠DGC=90°,
∵∠BAC=90°,
∴∠BAC=∠DGC,
∴AB∥DG,
∴∠BAD=∠ADG,
由(1)得∠1=∠BAD,
∴∠1=∠ADG,
∴DG平分∠ADC.………………………………………………………………………5分
21.
解:(1)根据题意得100×=30(个),所以红球有30个.
……2分
(2)设白球有x个,则黄球有(2x-5)个.
根据题意得x+2x-5=100-30,解得x=25.
所以摸出一个球是白球的概率为=;……………………………………………4分
(3)因为取走10个球后,还剩90个球,其中红球的个数没有变化,所以从剩余的球中摸出一个球是红球的概率为.……………………………………………4分
22.
解:(1)设甲种工具每件x元,乙种工具每件y元,
依题意得:,……………………………………………………………………3分
解得:.………………………………………………………………………2分
答:甲种工具每件16元,乙种工具每件4元.
(2)设甲种工具购买了m件,则乙种工具购买了(100﹣m)件,
依题意得:16m+4(100﹣m)≤1000,………………………………………3分
解得:m≤50.………………………………………………………………2分
答:甲种工具最多购买50件.
23.
证明:(1)∵∠ABC=∠DBE=90°,
∴∠ABE=∠CBD,
在△ABE和△CBD中,
,
∴△ABE≌△CBD(SAS),
∴AE=CD;…………………………………………………………………4分
(2)∵△ABE≌△CBD,
∴∠AEB=∠CDB,
∵∠AEB+∠DME=∠CDB+∠DBE,
∵∠DBE=90°,
∴∠DME=∠DBE=90°,
∴AE⊥CD;…………………………………………………………………4分
(3)过B分别作BP⊥AE,BQ⊥CD,垂足分别为P,Q,
∵△ABE≌△CBD,
∴S△ABE=S△CBD,AE=CD,
∴BP=BQ,
∴B点在∠AMD的平分线上,
即MB平分∠AMD.…………………………………………………4分
24(1)如图1中,作AH⊥BC于H.
∵AB=AC,AH⊥BC,∴∠BAH=∠CAH,
∵DE⊥AC,∴∠AHC=∠CED=90°,
∴∠C+∠CAH=90°,∠C+∠EDC=90°,
∴∠CAH=∠EDC,
∴∠BAC=2∠EDC.……………………………………4分
(2)如图2中,结论:∠BAC=2∠EDC.
理由:∵AB=AC,AH⊥BC,∴∠BAH=∠CAH,
∵DE⊥AC,∴∠AHC=∠CED=90°,
∴∠C+∠CAH=90°,∠C+∠EDC=90°,
∴∠CAH=∠EDC,
∴∠BAC=2∠EDC.……………………………………4分
(3)如图2中,设∠C=∠FAC=∠ABC=x,则∠BAF=∠BFA=2x,
∴5x=180°,
∴x=36°,∴∠EAK=∠ABC+∠C=72°,
∵KE⊥EC,
∴∠E=90°,
∴∠EKA=90°﹣72°=18°.……………………………………4分
七年级数学试题
(第11页,共8页)
七年级数学试题
一、选择题(本题有12小题,每小题5分,共60分,每小题只有一个选项是正确的,不选、多选、错选,均不得分)
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
1.已知关于的方程是二元一次方程,则的值为(
)
A.
B.
C.
D.
2.若m>n,则下列不等式一定成立的是( )
A.2m<3n
B.2+m>2+n
C.2﹣m>2﹣n
D.<
3.从分别标有数﹣3,﹣2,﹣1,0,1,2,3的七张没有明显差别的卡片中,随机抽取一张,所抽卡片上的数的绝对值不小于2的概率是( )
A.
B.
C.
D.
4.将一副直角三角板如图放置,使两直角边重合,则∠α的度数为( )
A.75°
B.105°
C.135°
D.165°
5.若不等式组无解,则a的取值范围为( )
A.a>4
B.a≤4
C.0<a<4
D.a≥4
6.直线l1∥l2,∠A=125°,∠B=85°,∠1=15°,则∠2=( )
第4题图
第6题图
第9题图
A.15°
B.25°
C.35°
D.20°
7.
下列命题中,其逆命题是假命题的是(
)
A.直角三角形两条直角边的平方和等于斜边的平方
B.角平分线上的点到这个角的两边的距离相等
C.如果a3=b3,那么a2=b2
D.两直线平行,内错角相等
8.
两位同学在解方程组时,甲同学由正确地解出,乙同学因把c写错了解得,则a+b+c的值为( )
A.3
B.0
C.1
D.7
9.如图,函数y=2x和y=ax+4的图象相交于点A(m,3),则不等式2x≤ax+4的解集为
A.
x≤3
B.
x≥3
C.
x≤
D.
x≥
10.如图,在Rt△ABC中,∠C=90°,BE平分∠ABC,ED垂直平分AB于D,若AC=9,则AE的值是( )
A.3
B.5
C.6
D.4
11.如图,已知GF⊥AB,∠1=∠2,∠B=∠AGH,则下列结论中:①GH∥BC;②∠D=∠F;③HE平分∠AHG;④HE⊥AB,其中正确的有( )
A.0个
B.1个
C.2个
D.3个
第10题图
第11题图
第12题图
12.
如图,AD是△ABC的角平分线,DF⊥AB于点F,且DE=DG,S△ADG=24,S△AED=18,则△DEF的面积为( )
A.2
B.3
C.4
D.6
二、填空题(共5小题,每小题4分,满分20分)
13.已知关于x的不等式组的整数解共有5个,则a的取值范围是
.
14.若方程组的解也是二元一次方程x﹣y=1的一个解,则a=
.
15.如图,“赵爽弦图”是吴国的赵爽创制的.以直角三角形的斜边为边长得到一个正方形,该正方形由4个全等的直角三角形再加上中间的小正方形组成,在一次游园活动中,数学小组制作了一面“赵爽弦图锣”,其中∠ABC=90°,AC=13cm,AB=5cm,小明蒙上眼睛用棍子击中了锣面,他击中阴影部分的概率是
.
16.如图,将一条对边互相平行的纸带进行两次折叠,折痕分别为AB,CD.若CD∥BE,∠1=28°,则∠2的度数是
.
第15题图
第16题图
第17题图
17.如图,已知△ABC中,AB=AC,AD是BC边上的中线,且∠BAD=40°.点E是边AC上的一点,若△ADE为等腰三角形,则∠EDC的度数是
.
三、解答题(共7小题,共70分)
18.
解下列方程组
(1)
(2)
19.
(1)解不等式组,并把解集在数轴上表示出来.
(2)求不等式组的整数解
20.
如图,AD∥EF,∠1+∠2=180°.
(1)若∠1=50°,求∠BAD的度数;
(2)若DG⊥AC,垂足为G,∠BAC=90°,试说明:DG平分∠ADC.
21.一个不透明的袋中装有红、黄、白三种颜色球共100个,它们除颜色外其他都相同,其中黄球个数是白球个数的2倍少5个.已知从袋中摸出一个球是红球的概率是.
(1)求袋中红球的个数;
(2)求从袋中摸出一个球是白球的概率;
(3)取走10个球(其中没有红球)后,求从剩余的球中摸出一个球是红球的概率.
22.为了美化校园,我校欲购进甲、乙两种工具,如果购买甲种3件,乙种2件,共需56元;如果购买甲种1件,乙种4件,共需32元.
(1)甲、乙两种工具每件各多少元?
(2)现要购买甲、乙两种工具共100件,总费用不超过1000元,那么甲种工具最多购买多少件?
23.如图,△ABC和△EBD中,∠ABC=∠DBE=90°,AB=CB,BE=BD,连接AE,CD,AE与CD交于点M,AE与BC交于点N.
(1)求证:AE=CD;
(2)求证:AE⊥CD;
(3)求证:MB平分∠AMD.
24.已知,在△ABC中,∠ABC=∠ACB,点D为射线CB上一点,过点D作DE⊥AC于点E.
(1)如图1,当点D在线段BC上时,请直接写出∠BAC与∠EDC的数量关系:
.
(2)如图2,当点D在CB的延长线上时,画出图形,探究∠BAC与∠EDC的数量关系,并说明理由.
(3)在(2)的条件下,点F为线段BC上一点,过点F作FG⊥AC于点G,连接AF,且∠AFG=∠CFG,∠BAF=∠BFA,延长ED、AB交于点K,求∠EKA的度数.
参考答案
一、选择题:本题共12小题,每小题5分,共60分
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
A
B
D
D
D
A
C
D
C
C
C
B
二、填空题:每小题4分,共20分。
13.
﹣3<a≤﹣2
14.
15.
16.56°
17.50°或20°
三、解答题:
18.(每小题4分,共8分)
解:(1)
原方程组的解是.……………………………………………………………4分
(2)
原方程组的解是.…………………………………………………………4分
19.(每小题4分,共8分)
(1)由(1)得:
由(2)得:
…………………3分
……………………………………………………………1分
(2)化简得
整理得:-1≤x<3.
…………………………………………………………………………3分
原不等式组的整数解为:x=-1,0,1,2.
………………………………………………1分
20.
(1)解:∵AD∥EF,
∴∠BAD+∠2=180°,
∵∠1+∠2=180°,
∴∠1=∠BAD,
∵∠1=50°,
∴∠BAD=50°;………………………………………………………………………5分
(2)证明:∵DG⊥AC,
∴∠DGC=90°,
∵∠BAC=90°,
∴∠BAC=∠DGC,
∴AB∥DG,
∴∠BAD=∠ADG,
由(1)得∠1=∠BAD,
∴∠1=∠ADG,
∴DG平分∠ADC.………………………………………………………………………5分
21.
解:(1)根据题意得100×=30(个),所以红球有30个.
……2分
(2)设白球有x个,则黄球有(2x-5)个.
根据题意得x+2x-5=100-30,解得x=25.
所以摸出一个球是白球的概率为=;……………………………………………4分
(3)因为取走10个球后,还剩90个球,其中红球的个数没有变化,所以从剩余的球中摸出一个球是红球的概率为.……………………………………………4分
22.
解:(1)设甲种工具每件x元,乙种工具每件y元,
依题意得:,……………………………………………………………………3分
解得:.………………………………………………………………………2分
答:甲种工具每件16元,乙种工具每件4元.
(2)设甲种工具购买了m件,则乙种工具购买了(100﹣m)件,
依题意得:16m+4(100﹣m)≤1000,………………………………………3分
解得:m≤50.………………………………………………………………2分
答:甲种工具最多购买50件.
23.
证明:(1)∵∠ABC=∠DBE=90°,
∴∠ABE=∠CBD,
在△ABE和△CBD中,
,
∴△ABE≌△CBD(SAS),
∴AE=CD;…………………………………………………………………4分
(2)∵△ABE≌△CBD,
∴∠AEB=∠CDB,
∵∠AEB+∠DME=∠CDB+∠DBE,
∵∠DBE=90°,
∴∠DME=∠DBE=90°,
∴AE⊥CD;…………………………………………………………………4分
(3)过B分别作BP⊥AE,BQ⊥CD,垂足分别为P,Q,
∵△ABE≌△CBD,
∴S△ABE=S△CBD,AE=CD,
∴BP=BQ,
∴B点在∠AMD的平分线上,
即MB平分∠AMD.…………………………………………………4分
24(1)如图1中,作AH⊥BC于H.
∵AB=AC,AH⊥BC,∴∠BAH=∠CAH,
∵DE⊥AC,∴∠AHC=∠CED=90°,
∴∠C+∠CAH=90°,∠C+∠EDC=90°,
∴∠CAH=∠EDC,
∴∠BAC=2∠EDC.……………………………………4分
(2)如图2中,结论:∠BAC=2∠EDC.
理由:∵AB=AC,AH⊥BC,∴∠BAH=∠CAH,
∵DE⊥AC,∴∠AHC=∠CED=90°,
∴∠C+∠CAH=90°,∠C+∠EDC=90°,
∴∠CAH=∠EDC,
∴∠BAC=2∠EDC.……………………………………4分
(3)如图2中,设∠C=∠FAC=∠ABC=x,则∠BAF=∠BFA=2x,
∴5x=180°,
∴x=36°,∴∠EAK=∠ABC+∠C=72°,
∵KE⊥EC,
∴∠E=90°,
∴∠EKA=90°﹣72°=18°.……………………………………4分
七年级数学试题
(第11页,共8页)
同课章节目录
