山东省淄博市高青县2020-2021学年第二学期(五四学制)八年级数学期末试题(word版,含答案)
文档属性
| 名称 | 山东省淄博市高青县2020-2021学年第二学期(五四学制)八年级数学期末试题(word版,含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 195.1KB | ||
| 资源类型 | 素材 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-15 17:27:10 | ||
图片预览




文档简介
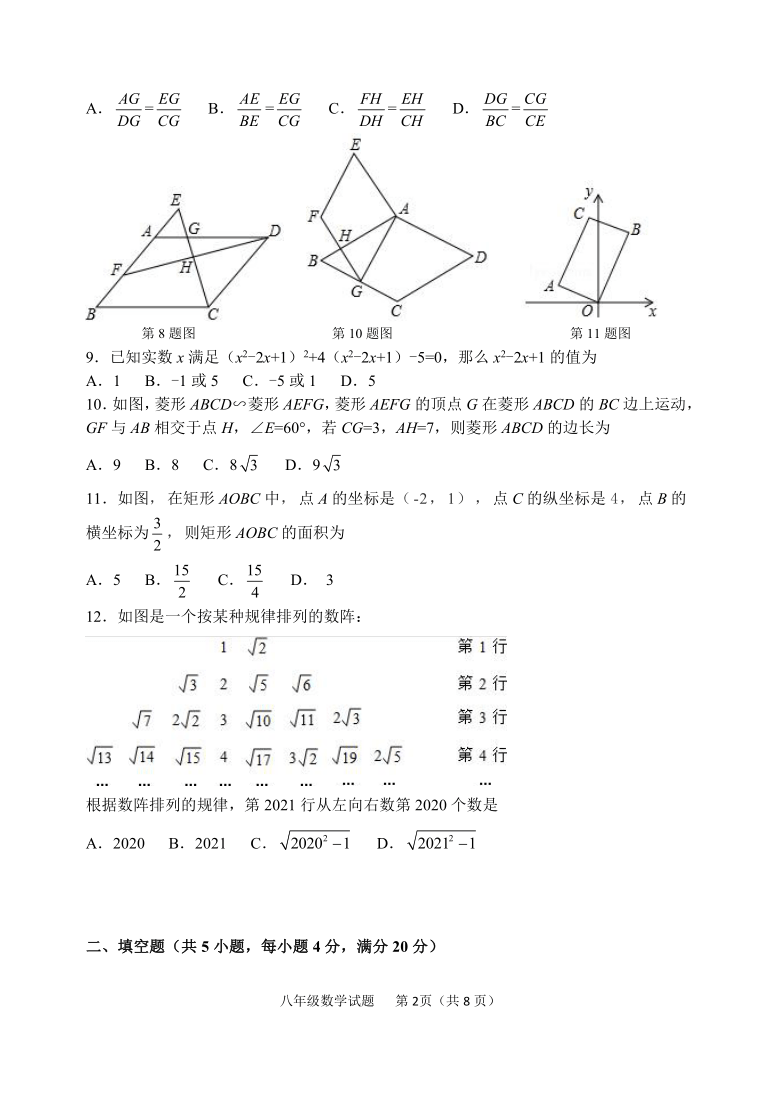
2020—2021学年度第二学期期末初三数学试题
一、选择题(本题有12小题,每小题5分,共60分,每小题只有一个选项是正确的,不选、多选、错选,均不得分)
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
1.下列方程是一元二次方程的是
A.x+y-1=0
B.x2+=2
C.x2=2x+3
D.xy=-6
2.若3a=2b,则的值为
A.
B.
C.
D.
3.若使算式3〇的运算结果最小,则〇表示的运算符号是
A.+
B.-
C.×
D.÷
4.如图,矩形ABCD的对角线AC=8cm,∠BOC=120°,则BC的长为
A.2cm
B.4cm
C.4cm
D.8cm
第4题图
第6题图
5.已知x=+2,则代数式x2-x-2的值为
A.9+5
B.9+3
C.5+5
D.5+3
6.如图,在菱形ABCD中,∠ABC=80°,E是线段BD上一动点(点E不与点B,D重合),当△ABE是等腰三角形时,∠DAE=
A.30°
B.70°
C.30°或60°
D.40°或70°
7.若x1,x2是方程x2-4x-2020=0的两个实数根,则代数式x12-2x1+2x2的值等于
A.2020
B.2019
C.2029
D.2028
8.如图,在平行四边形ABCD中,点E、F分别是AB及BA延长线上一点,连接CE、DF相交于点H,CE交AD于点G,下列结论错误的是
A.=
B.=
C.=
D.=
第8题图
第10题图
第11题图
9.已知实数x满足(x2-2x+1)2+4(x2-2x+1)-5=0,那么x2-2x+1的值为
A.1
B.-1或5
C.-5或1
D.5
10.如图,菱形ABCD∽菱形AEFG,菱形AEFG的顶点G在菱形ABCD的BC边上运动,GF与AB相交于点H,∠E=60°,若CG=3,AH=7,则菱形ABCD的边长为
A.9
B.8
C.8
D.9
11.如图,在矩形AOBC中,点A的坐标是(-2,1),点C的纵坐标是4,点B的横坐标为,则矩形AOBC的面积为
A.5
B.
C.
D.
3
12.如图是一个按某种规律排列的数阵:
根据数阵排列的规律,第2021行从左向右数第2020个数是
A.2020
B.2021
C.
D.
二、填空题(共5小题,每小题4分,满分20分)
13.计算-2等于
.
14.若关于x的一元二次方程(m-1)x2-4x+1=0有两个不相等的实数根,则m的取值范围为
.
15.如图,用一段篱笆靠墙围成一个大长方形花圃(靠墙处不用篱笆),中间用篱笆隔开分成两个小长方形区域,分别种植两种花草,篱笆总长为17米(恰好用完),围成的大长方形花圃的面积为24平方米,设垂直于墙的一段篱笆长为x米,可列出方程为
.
第15题图
第16题图
第17题图
16.如图,正方形DEFG的边EF在△ABC的边BC上,顶点D、G分别在边AB、AC上.已知△ABC的边BC=16cm,高AH为10cm,则正方形DEFG的边长为
cm.
17.如图所示,在正方形ABCD中,点E在AB边上,BE=4,M是对角线BD上的一点(∠EMB是锐角),连接EM,EM=5,过点M作MN⊥EM交BC边于点N.过点N作NH⊥BD于H,则△HMN的面积=
.
三、解答题(共7小题,共70分)
18.解答下列各题
(1)计算:.
(2)解方程:3x2-x-4=0.
19.如图,在△ABC中,点D在AB边上,∠ABC=∠ACD.
(1)求证:△ABC∽△ACD;
(2)若AD=4,AB=9,求AC的长.
20.已知关于x的一元二次方程(m-2)x2-2x+1=0有两个实数根.
(1)求m的取值范围;
(2)在1,2,4三个数中,取一个合适的m值代入方程,并解这个方程.
21.某商场以每件220元的价格购进一批商品,当每件商品售价为280元时,每天可售出30件,为了迎接“618购物节”,扩大销售,商场决定采取适当降价的方式促销,经调查发现,如果每件商品降价1元,那么商场每天就可以多售出3件.
(1)降价前商场每天销售该商品的利润是多少元?
(2)要使商场每天销售这种商品的利润达到降价前每天利润的两倍,且更有利于减少库存,则每件商品应降价多少元?
22.如图,在正方形ABCD中,在BC边上取中点E,连接DE,过点E做EF⊥ED交AB于点G、交AD延长线于点F.
(1)求证:△ECD∽△DEF;
(2)若CD=4,求AF的长.
23.【阅读材料】把形如ax2+bx+c的二次三项式(或其一部分)经过适当变形配成完全平方式的方法叫配方法,配方法在因式分解、证明恒等式、利用a2≥0求代数式最值等问题中都有广泛应用.
例如:利用配方法将x2-6x+8变形为a(x+m)2+n的形式,并把二次三项式分解因式.
配方:x2-6x+8=x2-6x+32-32+8=(x-3)2-1
分解因式:x2-6x+8=(x-3)2-1=(x-3+1)(x-3-1)=(x-2)(x-4)
【解决问题】根据以上材料,解答下列问题:
(1)利用配方法将多项式x2-4x-5化成a(x+m)2+n的形式.
(2)利用配方法把二次三项式x2-2x-35分解因式.
(3)若a、b、c分别是△ABC的三边,且a2+2b2+3c2-2ab-2b-6c+4=0,试判断△ABC的形状,并说明理由.
(4)求证:无论x,y取任何实数,代数式x2+y2+4x-6y+15的值恒为正数.
24.如图,在菱形ABCD中,∠ABC=60°,M为AD的中点,连接BM,交AC于E,在CB上取一点F,使得CF=AE,连接AF,交BM于G,连接CG.
(1)求∠BGF的度数;
(2)求的值;
(3)求证:BG⊥CG.
数学参考答案
一、选择题:本题共12小题,每小题5分,共60分
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
C
A
B
C
D
C
D
B
A
A
B
D
二、填空题:每小题4分,共20分
题号
13
14
15
16
17
答案
m<5且m≠1
x(17-3x)=24
6
三、解答题:
18.(1)解:原式=2+4×-×3+3×
=2+2-2+=3.………………………………4分
(2)解:∵3x2-x-4=0,∴(x+1)(3x-4)=0,
则x+1=0或3x-4=0,解得x=-1或x=.………………………8分
19.(1)证明:∵∠ABC=∠ACD,∠A=∠A,
∴△ABC∽△ACD;……………………4分
(2)解:∵△ABC∽△ACD,
∴=,即=,
∴AC=6.…………………………………8分
20.解:(1)根据题意,b2-4ac=(-2)2-4(m-2)≥0,且m-2≠0,
∴m≤3,m≠2;…………………………………………5分
(2)∵m≤3且m≠2,
∴可取m=1,
当m=1时,原方程化为-x2-2x+1=0,
∴x=,
解得x1=-1-,x2=-1+.…………………………10分
21.解:(1)(280-220)×30=1800?(元).
∴降价前商场每天销售该商品的利润是1800元.………………………………5分
(2)设每件商品应降价x元,
由题意,得?(280-x-220)(30+3x)=1800×2,
解得?x1=20,x2=30.
∵要更有利于减少库存,∴x=30.
答:每件商品应降价30元.…………………………………………………………10分
22.解:(1)证明:∵四边形ABCD是正方形,EF⊥ED,
∴∠FED=∠C=90°,BC∥AD,∴∠CED=∠FDE,
∴△ECD∽△DEF;………………………………………………………………4分
(2)解:∵四边形ABCD是正方形,∴∠C=90°,AD=BC=CD=4,
∵E为BC的中点,∴CE=BC=2,
在Rt△DCE中,由勾股定理得:DE===2,
∵△ECD∽△DEF,∴=,∴=,解得:DF=10,
∵AD=4,∴AF=DF-AD=10-4=6.…………………………………………………10分
23.解:(1)x2-4x-5=x2-4x+22-22-5=(x-2)2-9.…………………………3分
(2)x2-2x-35=x2-2x+1-1-35=(x-1)2-62
=(x-1+6)(x-1-6)=(x+5)(x-7).………………………………………6分
(3)△ABC为等边三角形,理由如下:
∵a2+2b2+3c2-2ab-2b-6c+4=0,
∴(a2-2ab+b2)+(b2-2b+1)+3(c2-2c+1)=0,
∴(a-b)2+(b-1)2+3(c-1)2=0,
∵(a-b)2≥0,(b-1)2≥0,3(c-1)2≥0,
∴a-b=0,b-1=0,c-1=0,
∴a=b,b=1,c=1,
∴a=b=c,
∴△ABC为等边三角形.……………………………………………………………9分
(4)证明:x2+y2+4x-6y+15
=x2+4x+4+y2-6y+9+2
=(x+2)2+(y-3)2+2,
∵(x+2)2≥0,(y-3)2≥0,
∴(x+2)2+(y-3)2+2≥2,
∴代数式x2+y2+4x-6y+15的值恒为正数.…………………………………………12分
24.解:(1)∵四边形ABCD是菱形,
∴AB=BC=CD=AD,∠ABC=∠ADC=60°,
∴△ABC,△ADC都是等边三角形,
∴AB=AC,∠BAE=∠ACF=60°,
∵AE=CF,
∴△BAE≌△ACF(SAS),
∴∠ABE=∠CAF,
∴∠BGF=∠ABE+∠BAG=∠CAF+∠BAG=∠BAC=60°.……………………………4分
(2)∵∠BAG+∠ABG=∠ABG+∠CBM=60°,
∴∠BAG=∠CBM,
∵AD∥CB,∴∠AMB=∠CBM,∴∠BAG=∠BMA,
∵∠ABG=∠ABM,∴△BAG∽△BMA,∴=,∴=,
∵AM=MD=AD=AB,
∴=.…………………………………………8分
(3)连结CM.∵△ACD是等边三角形,∴CM⊥AD,
∴CM⊥BC,∴∠BCM=90°,
由(2)知△BAG∽△BMA,∴,
∵BC=BA,∴,∴
∵∠CBG=∠MBC,∴△BCG∽△BMC,
∴∠BGC=∠BCM=90°,∴BG⊥CG.…………………………………………12分
八年级数学试题
第11页(共8页)
一、选择题(本题有12小题,每小题5分,共60分,每小题只有一个选项是正确的,不选、多选、错选,均不得分)
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
1.下列方程是一元二次方程的是
A.x+y-1=0
B.x2+=2
C.x2=2x+3
D.xy=-6
2.若3a=2b,则的值为
A.
B.
C.
D.
3.若使算式3〇的运算结果最小,则〇表示的运算符号是
A.+
B.-
C.×
D.÷
4.如图,矩形ABCD的对角线AC=8cm,∠BOC=120°,则BC的长为
A.2cm
B.4cm
C.4cm
D.8cm
第4题图
第6题图
5.已知x=+2,则代数式x2-x-2的值为
A.9+5
B.9+3
C.5+5
D.5+3
6.如图,在菱形ABCD中,∠ABC=80°,E是线段BD上一动点(点E不与点B,D重合),当△ABE是等腰三角形时,∠DAE=
A.30°
B.70°
C.30°或60°
D.40°或70°
7.若x1,x2是方程x2-4x-2020=0的两个实数根,则代数式x12-2x1+2x2的值等于
A.2020
B.2019
C.2029
D.2028
8.如图,在平行四边形ABCD中,点E、F分别是AB及BA延长线上一点,连接CE、DF相交于点H,CE交AD于点G,下列结论错误的是
A.=
B.=
C.=
D.=
第8题图
第10题图
第11题图
9.已知实数x满足(x2-2x+1)2+4(x2-2x+1)-5=0,那么x2-2x+1的值为
A.1
B.-1或5
C.-5或1
D.5
10.如图,菱形ABCD∽菱形AEFG,菱形AEFG的顶点G在菱形ABCD的BC边上运动,GF与AB相交于点H,∠E=60°,若CG=3,AH=7,则菱形ABCD的边长为
A.9
B.8
C.8
D.9
11.如图,在矩形AOBC中,点A的坐标是(-2,1),点C的纵坐标是4,点B的横坐标为,则矩形AOBC的面积为
A.5
B.
C.
D.
3
12.如图是一个按某种规律排列的数阵:
根据数阵排列的规律,第2021行从左向右数第2020个数是
A.2020
B.2021
C.
D.
二、填空题(共5小题,每小题4分,满分20分)
13.计算-2等于
.
14.若关于x的一元二次方程(m-1)x2-4x+1=0有两个不相等的实数根,则m的取值范围为
.
15.如图,用一段篱笆靠墙围成一个大长方形花圃(靠墙处不用篱笆),中间用篱笆隔开分成两个小长方形区域,分别种植两种花草,篱笆总长为17米(恰好用完),围成的大长方形花圃的面积为24平方米,设垂直于墙的一段篱笆长为x米,可列出方程为
.
第15题图
第16题图
第17题图
16.如图,正方形DEFG的边EF在△ABC的边BC上,顶点D、G分别在边AB、AC上.已知△ABC的边BC=16cm,高AH为10cm,则正方形DEFG的边长为
cm.
17.如图所示,在正方形ABCD中,点E在AB边上,BE=4,M是对角线BD上的一点(∠EMB是锐角),连接EM,EM=5,过点M作MN⊥EM交BC边于点N.过点N作NH⊥BD于H,则△HMN的面积=
.
三、解答题(共7小题,共70分)
18.解答下列各题
(1)计算:.
(2)解方程:3x2-x-4=0.
19.如图,在△ABC中,点D在AB边上,∠ABC=∠ACD.
(1)求证:△ABC∽△ACD;
(2)若AD=4,AB=9,求AC的长.
20.已知关于x的一元二次方程(m-2)x2-2x+1=0有两个实数根.
(1)求m的取值范围;
(2)在1,2,4三个数中,取一个合适的m值代入方程,并解这个方程.
21.某商场以每件220元的价格购进一批商品,当每件商品售价为280元时,每天可售出30件,为了迎接“618购物节”,扩大销售,商场决定采取适当降价的方式促销,经调查发现,如果每件商品降价1元,那么商场每天就可以多售出3件.
(1)降价前商场每天销售该商品的利润是多少元?
(2)要使商场每天销售这种商品的利润达到降价前每天利润的两倍,且更有利于减少库存,则每件商品应降价多少元?
22.如图,在正方形ABCD中,在BC边上取中点E,连接DE,过点E做EF⊥ED交AB于点G、交AD延长线于点F.
(1)求证:△ECD∽△DEF;
(2)若CD=4,求AF的长.
23.【阅读材料】把形如ax2+bx+c的二次三项式(或其一部分)经过适当变形配成完全平方式的方法叫配方法,配方法在因式分解、证明恒等式、利用a2≥0求代数式最值等问题中都有广泛应用.
例如:利用配方法将x2-6x+8变形为a(x+m)2+n的形式,并把二次三项式分解因式.
配方:x2-6x+8=x2-6x+32-32+8=(x-3)2-1
分解因式:x2-6x+8=(x-3)2-1=(x-3+1)(x-3-1)=(x-2)(x-4)
【解决问题】根据以上材料,解答下列问题:
(1)利用配方法将多项式x2-4x-5化成a(x+m)2+n的形式.
(2)利用配方法把二次三项式x2-2x-35分解因式.
(3)若a、b、c分别是△ABC的三边,且a2+2b2+3c2-2ab-2b-6c+4=0,试判断△ABC的形状,并说明理由.
(4)求证:无论x,y取任何实数,代数式x2+y2+4x-6y+15的值恒为正数.
24.如图,在菱形ABCD中,∠ABC=60°,M为AD的中点,连接BM,交AC于E,在CB上取一点F,使得CF=AE,连接AF,交BM于G,连接CG.
(1)求∠BGF的度数;
(2)求的值;
(3)求证:BG⊥CG.
数学参考答案
一、选择题:本题共12小题,每小题5分,共60分
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
C
A
B
C
D
C
D
B
A
A
B
D
二、填空题:每小题4分,共20分
题号
13
14
15
16
17
答案
m<5且m≠1
x(17-3x)=24
6
三、解答题:
18.(1)解:原式=2+4×-×3+3×
=2+2-2+=3.………………………………4分
(2)解:∵3x2-x-4=0,∴(x+1)(3x-4)=0,
则x+1=0或3x-4=0,解得x=-1或x=.………………………8分
19.(1)证明:∵∠ABC=∠ACD,∠A=∠A,
∴△ABC∽△ACD;……………………4分
(2)解:∵△ABC∽△ACD,
∴=,即=,
∴AC=6.…………………………………8分
20.解:(1)根据题意,b2-4ac=(-2)2-4(m-2)≥0,且m-2≠0,
∴m≤3,m≠2;…………………………………………5分
(2)∵m≤3且m≠2,
∴可取m=1,
当m=1时,原方程化为-x2-2x+1=0,
∴x=,
解得x1=-1-,x2=-1+.…………………………10分
21.解:(1)(280-220)×30=1800?(元).
∴降价前商场每天销售该商品的利润是1800元.………………………………5分
(2)设每件商品应降价x元,
由题意,得?(280-x-220)(30+3x)=1800×2,
解得?x1=20,x2=30.
∵要更有利于减少库存,∴x=30.
答:每件商品应降价30元.…………………………………………………………10分
22.解:(1)证明:∵四边形ABCD是正方形,EF⊥ED,
∴∠FED=∠C=90°,BC∥AD,∴∠CED=∠FDE,
∴△ECD∽△DEF;………………………………………………………………4分
(2)解:∵四边形ABCD是正方形,∴∠C=90°,AD=BC=CD=4,
∵E为BC的中点,∴CE=BC=2,
在Rt△DCE中,由勾股定理得:DE===2,
∵△ECD∽△DEF,∴=,∴=,解得:DF=10,
∵AD=4,∴AF=DF-AD=10-4=6.…………………………………………………10分
23.解:(1)x2-4x-5=x2-4x+22-22-5=(x-2)2-9.…………………………3分
(2)x2-2x-35=x2-2x+1-1-35=(x-1)2-62
=(x-1+6)(x-1-6)=(x+5)(x-7).………………………………………6分
(3)△ABC为等边三角形,理由如下:
∵a2+2b2+3c2-2ab-2b-6c+4=0,
∴(a2-2ab+b2)+(b2-2b+1)+3(c2-2c+1)=0,
∴(a-b)2+(b-1)2+3(c-1)2=0,
∵(a-b)2≥0,(b-1)2≥0,3(c-1)2≥0,
∴a-b=0,b-1=0,c-1=0,
∴a=b,b=1,c=1,
∴a=b=c,
∴△ABC为等边三角形.……………………………………………………………9分
(4)证明:x2+y2+4x-6y+15
=x2+4x+4+y2-6y+9+2
=(x+2)2+(y-3)2+2,
∵(x+2)2≥0,(y-3)2≥0,
∴(x+2)2+(y-3)2+2≥2,
∴代数式x2+y2+4x-6y+15的值恒为正数.…………………………………………12分
24.解:(1)∵四边形ABCD是菱形,
∴AB=BC=CD=AD,∠ABC=∠ADC=60°,
∴△ABC,△ADC都是等边三角形,
∴AB=AC,∠BAE=∠ACF=60°,
∵AE=CF,
∴△BAE≌△ACF(SAS),
∴∠ABE=∠CAF,
∴∠BGF=∠ABE+∠BAG=∠CAF+∠BAG=∠BAC=60°.……………………………4分
(2)∵∠BAG+∠ABG=∠ABG+∠CBM=60°,
∴∠BAG=∠CBM,
∵AD∥CB,∴∠AMB=∠CBM,∴∠BAG=∠BMA,
∵∠ABG=∠ABM,∴△BAG∽△BMA,∴=,∴=,
∵AM=MD=AD=AB,
∴=.…………………………………………8分
(3)连结CM.∵△ACD是等边三角形,∴CM⊥AD,
∴CM⊥BC,∴∠BCM=90°,
由(2)知△BAG∽△BMA,∴,
∵BC=BA,∴,∴
∵∠CBG=∠MBC,∴△BCG∽△BMC,
∴∠BGC=∠BCM=90°,∴BG⊥CG.…………………………………………12分
八年级数学试题
第11页(共8页)
同课章节目录
