2012年高一数学新课程教学课件:1.3.1交集与并集(北师大版必修1)
文档属性
| 名称 | 2012年高一数学新课程教学课件:1.3.1交集与并集(北师大版必修1) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-05-15 00:00:00 | ||
图片预览







文档简介
(共22张PPT)
§3 集合的基本运算
3.1 交集与并集
理解两个集合的交集与并集的含义,会求两个简单集合的交集与并集。
能使用Venn图表达集合的关系及运算,体会直观图示对理解抽象概念的作用.
能够正确的理解不同语言表示的集合的本质并且能够在解题时准确表达.
实数有加减乘除的基本运算,集合是否有类似的运算法则呢 ?
引入新课
考察下列各个集合,你能说出集合A,B与集合C之间的关系吗
A={2,4,6,8,10}, B={3,5,8,12} ,C={8};
(2)A={x|x是新华中学2011年9月在校的女同学},
B={x|x是新华中学2011年9月入学的高一级同学},
C={x|x是新华中学2011年9月入学的高一级女同学}.
实例分析
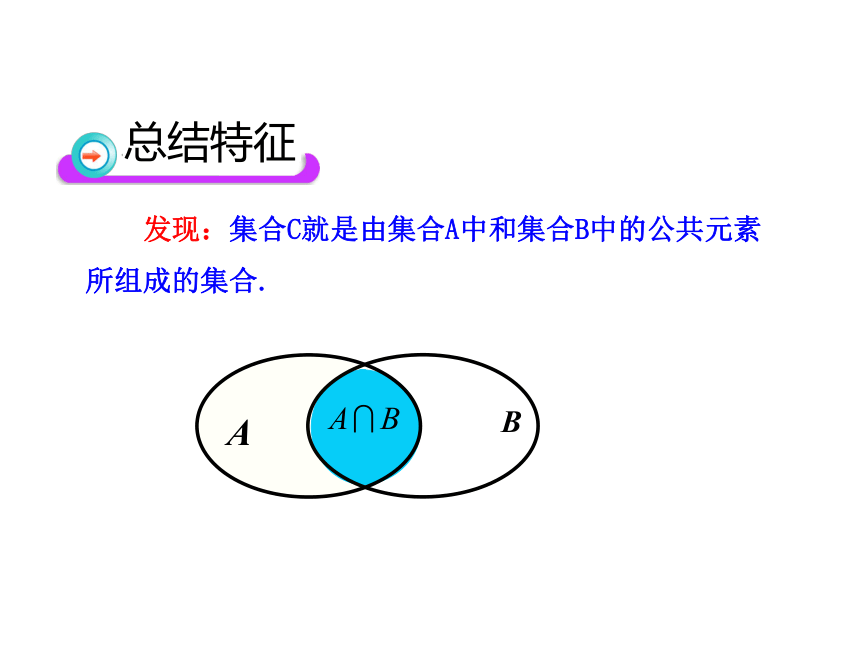
发现:集合C就是由集合A中和集合B中的公共元素所组成的集合.
总结特征
一般地,由既属于集合A又属于集合B的所有元素组成的集合,叫作A与B的交集,记作A∩B,(读作“A交B”),即
A∩B={x|x∈A,且x∈B}.
抽象概括
A
B
A∩B
1、新华中学开运动会,设
A={x|x是新华中学高一年级参加百米赛跑的同学}
B={x|x是新华中学高一年级参加跳高比赛的同学},
求A∩B.
解:A∩B={x|x是新华中学高一年级既参加百米赛跑又参加跳高比赛的同学}.
概念巩固
解:
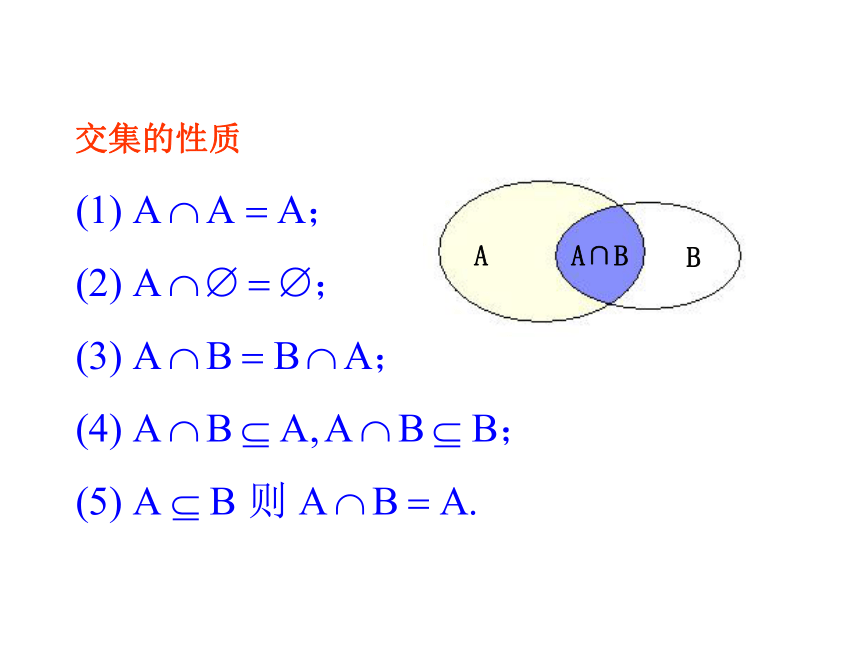
交集的性质
A
B
A∩B
考察下列各个集合,你能说出集合C与集合A,B之间的关系吗
(1) A={1,3,5}, B={2,4,6} ,C={1,2,3,4,5,6}
(2) A={x|x是有理数},B={x|x是无理数},
C={x|x是实数}.
实例分析
发现:集合C(阴影部分)就是由集合A中和集合B中的所有公共元素所组成的集合.
A
B
C
总结特征
一般地,由属于集合A或属于集合B的所有元素组成的集合,叫作A与B的并集,记作A∪B,(读作“A并B”).即
A∪B={x|x∈A,或x∈B}
抽象概括
1、A={4,5,6,8}, B={3,5,7,8},求A∪B.
2、设集合A={x|x为等腰三角形},集合B={x|x为直角三角形},求A∪B.
A∪B={3,4,5,6,7,8}.
A∪B={x|x为等腰三角形或直角三角形}.
概念巩固
并集的性质
例1 某学校所有男生组成集合A,一年级的所有学生组成集合B,一年级的所有男生组成集合C,一年级的所有女生组成集合D.求
例题分析
例2 设A={x|x是不大于10的正奇数},B={x|x是12的正约数}.求
解: A={x|x是不大于10的正奇数}={1,3,5,7,9},
B={x|x是12的正约数}={1,2,3,4,6,12},
举例验证下列等式,并与同学讨论交流:
思考交流
1、设A={x x是锐角三角形},
则A∩B=___________;
A∪B= .
{x|x是斜三角形}
B={x x是钝角三角形},
2、设A={x︱x>-2},B={x︱x<3},求A∩B,A∪B.
解: A∩B ={x|-2A∪B=R .
3、 已知A={2,-1,x2-x+1}, B={2y,-4,x+4},
C={-1,7}且A∩B=C,求x,y的值及A∪B.
1. 理解两个集合交集与并集的概念和性质.
2. 求两个集合的交集与并集,常用数轴法和
图示法.
3.注意灵活、准确地运用性质解题;
§3 集合的基本运算
3.1 交集与并集
理解两个集合的交集与并集的含义,会求两个简单集合的交集与并集。
能使用Venn图表达集合的关系及运算,体会直观图示对理解抽象概念的作用.
能够正确的理解不同语言表示的集合的本质并且能够在解题时准确表达.
实数有加减乘除的基本运算,集合是否有类似的运算法则呢 ?
引入新课
考察下列各个集合,你能说出集合A,B与集合C之间的关系吗
A={2,4,6,8,10}, B={3,5,8,12} ,C={8};
(2)A={x|x是新华中学2011年9月在校的女同学},
B={x|x是新华中学2011年9月入学的高一级同学},
C={x|x是新华中学2011年9月入学的高一级女同学}.
实例分析
发现:集合C就是由集合A中和集合B中的公共元素所组成的集合.
总结特征
一般地,由既属于集合A又属于集合B的所有元素组成的集合,叫作A与B的交集,记作A∩B,(读作“A交B”),即
A∩B={x|x∈A,且x∈B}.
抽象概括
A
B
A∩B
1、新华中学开运动会,设
A={x|x是新华中学高一年级参加百米赛跑的同学}
B={x|x是新华中学高一年级参加跳高比赛的同学},
求A∩B.
解:A∩B={x|x是新华中学高一年级既参加百米赛跑又参加跳高比赛的同学}.
概念巩固
解:
交集的性质
A
B
A∩B
考察下列各个集合,你能说出集合C与集合A,B之间的关系吗
(1) A={1,3,5}, B={2,4,6} ,C={1,2,3,4,5,6}
(2) A={x|x是有理数},B={x|x是无理数},
C={x|x是实数}.
实例分析
发现:集合C(阴影部分)就是由集合A中和集合B中的所有公共元素所组成的集合.
A
B
C
总结特征
一般地,由属于集合A或属于集合B的所有元素组成的集合,叫作A与B的并集,记作A∪B,(读作“A并B”).即
A∪B={x|x∈A,或x∈B}
抽象概括
1、A={4,5,6,8}, B={3,5,7,8},求A∪B.
2、设集合A={x|x为等腰三角形},集合B={x|x为直角三角形},求A∪B.
A∪B={3,4,5,6,7,8}.
A∪B={x|x为等腰三角形或直角三角形}.
概念巩固
并集的性质
例1 某学校所有男生组成集合A,一年级的所有学生组成集合B,一年级的所有男生组成集合C,一年级的所有女生组成集合D.求
例题分析
例2 设A={x|x是不大于10的正奇数},B={x|x是12的正约数}.求
解: A={x|x是不大于10的正奇数}={1,3,5,7,9},
B={x|x是12的正约数}={1,2,3,4,6,12},
举例验证下列等式,并与同学讨论交流:
思考交流
1、设A={x x是锐角三角形},
则A∩B=___________;
A∪B= .
{x|x是斜三角形}
B={x x是钝角三角形},
2、设A={x︱x>-2},B={x︱x<3},求A∩B,A∪B.
解: A∩B ={x|-2
3、 已知A={2,-1,x2-x+1}, B={2y,-4,x+4},
C={-1,7}且A∩B=C,求x,y的值及A∪B.
1. 理解两个集合交集与并集的概念和性质.
2. 求两个集合的交集与并集,常用数轴法和
图示法.
3.注意灵活、准确地运用性质解题;
