2012年高一数学新课程教学课件:1.3.2全集与补集(北师大版必修1)
文档属性
| 名称 | 2012年高一数学新课程教学课件:1.3.2全集与补集(北师大版必修1) |

|
|
| 格式 | zip | ||
| 文件大小 | 950.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-05-15 00:00:00 | ||
图片预览




文档简介
(共19张PPT)
3.2 全集与补集
在理解两个集合交集与并集含义的基础上理解全集和补集的概念.
能使用Venn图表达集合的关系和运算,体会直观图示对理解抽象概念的作用.
能够正确的理解不同语言表示的集合的本质并且能够在解题时准确表达.
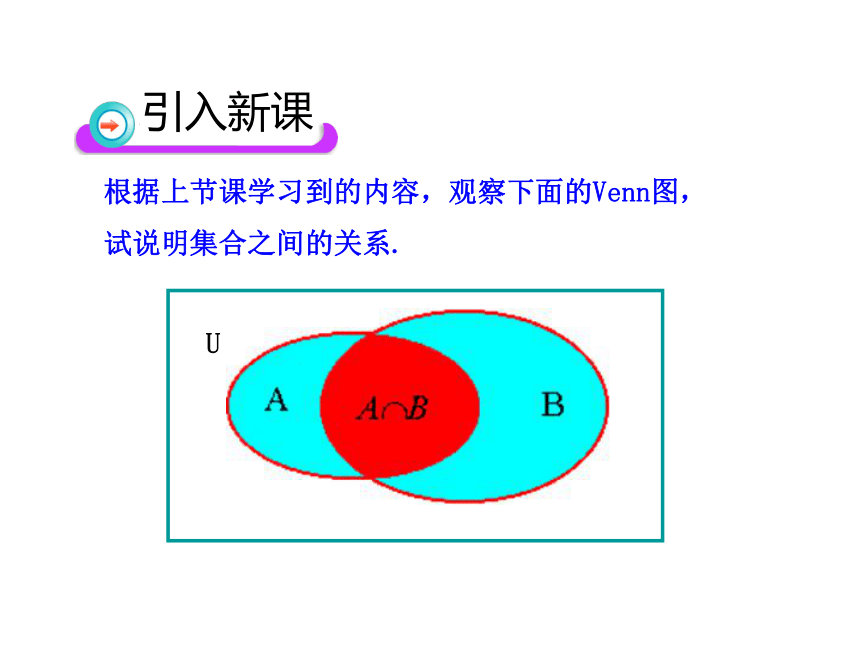
根据上节课学习到的内容,观察下面的Venn图,试说明集合之间的关系.
引入新课
U
U
试分析以下三个集合的关系:
A={x|x是本班同学},
B={x|x是本班男生},
C={x|x是本班女生}.
发现:集合C就是集合A中的元素除去集合B中的元素后余下来的元素所组成的集合.
实例分析
1. 全集
在研究某些集合的时候,这些集合往往是某个给定集合的子集,这个给定的集合叫作全集,常用符号U表示.全集含有我们所要研究的这些集合的全部元素.
注意:全集是相对于所研究问题而言的一个相对概念,它含有与所研究问题有关的各个集合的全部元素.因此全集因问题而异.例如在研究数集时,常常把实数集看作全集.
抽象概括
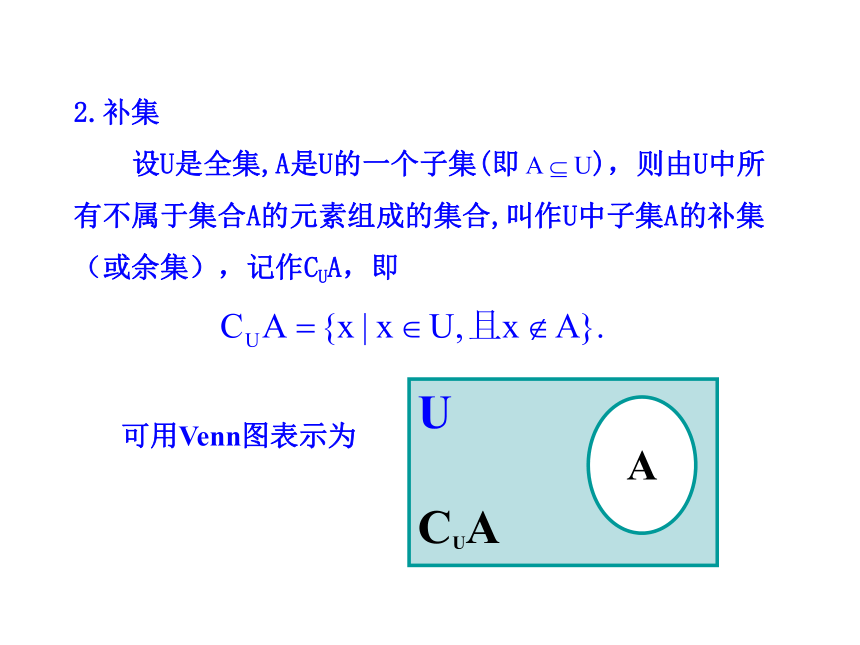
可用Venn图表示为
U
CUA
A
2.补集
设U是全集,A是U的一个子集(即 ),则由U中所有不属于集合A的元素组成的集合,叫作U中子集A的补集(或余集),记作CUA,即
若设全集U为全体实数集,A是有理数集,那么U中A的补集就为无理数集,想一想,你是否还能举出身边的例子呢?
想一想?
3.性质
1.设U={x|x是小于9的正整数},A={1,2,3},B={3,4,5,6},求CUA, CUB.
知识强化
解:据题意知U={1,2,3,4,5,6,7,8},故
CUA= {4,5,6,7,8,9}, CUB ={1,2,7,8}
2. 设U={x|x是三角形},A={x|x是锐角三角形},B={x|x是钝角三角形}.求A∩B, CU (A∪B).
解:由题意知A∩B= ,
CU(A∪B)={x|x是直角三角形}.
例1 试用集合A,B的交集、并集、补集分别表示下图中Ⅰ、Ⅱ、Ⅲ、Ⅳ四个部分所表示的集合.
U
Ⅰ
A
B
Ⅱ
Ⅲ
Ⅳ
解:Ⅰ部分:
Ⅱ部分:
Ⅲ部分:
Ⅳ部分:
例题分析
5
4
3
-1
1
0
2
6
x
5
4
1
3
-1
0
2
6
x
(3)在数轴上,画出集合CRA,CRB如图示
_________.
______________.
4.已知全集U={1,2,3,4,5,6,7},A={2,4,5},
B={1,3,5,7}求A∩(CUB),(CUA)∩ (CUB).
解:由题意可知
CUA={1,3,6,7}, CUB={2,4,6},
则A∩(CUB)={2,4},
(CUA)∩ (CUB)={6}.
若a≠1,且a≠4,a≠3,则A∪B={1,3,4,a},
A∩B= .
若a=3,则A∪B={1,3,4} ,A∩B= ,
5.设集合A={x|(x-3)(x-a)=0,a∈R},
B={x|(x-4)(x-1)=0},求A∪B,A∩B.
解:由题意可知
B={1,4}, A={a,3},
若a=1,则A∪B={1,3,4} ,A∩B={1};
若a=4,则A∪B={1,3,4} ,A∩B={4},
本节我们在集合的并、交两种基本运算的基础上学习了全集和补集的概念,在掌握概念的基础上能够熟练运用自然语言、符号语言、图形语言来表示和理解集合的全集和补集以及并集、交集的综合运算.
3.2 全集与补集
在理解两个集合交集与并集含义的基础上理解全集和补集的概念.
能使用Venn图表达集合的关系和运算,体会直观图示对理解抽象概念的作用.
能够正确的理解不同语言表示的集合的本质并且能够在解题时准确表达.
根据上节课学习到的内容,观察下面的Venn图,试说明集合之间的关系.
引入新课
U
U
试分析以下三个集合的关系:
A={x|x是本班同学},
B={x|x是本班男生},
C={x|x是本班女生}.
发现:集合C就是集合A中的元素除去集合B中的元素后余下来的元素所组成的集合.
实例分析
1. 全集
在研究某些集合的时候,这些集合往往是某个给定集合的子集,这个给定的集合叫作全集,常用符号U表示.全集含有我们所要研究的这些集合的全部元素.
注意:全集是相对于所研究问题而言的一个相对概念,它含有与所研究问题有关的各个集合的全部元素.因此全集因问题而异.例如在研究数集时,常常把实数集看作全集.
抽象概括
可用Venn图表示为
U
CUA
A
2.补集
设U是全集,A是U的一个子集(即 ),则由U中所有不属于集合A的元素组成的集合,叫作U中子集A的补集(或余集),记作CUA,即
若设全集U为全体实数集,A是有理数集,那么U中A的补集就为无理数集,想一想,你是否还能举出身边的例子呢?
想一想?
3.性质
1.设U={x|x是小于9的正整数},A={1,2,3},B={3,4,5,6},求CUA, CUB.
知识强化
解:据题意知U={1,2,3,4,5,6,7,8},故
CUA= {4,5,6,7,8,9}, CUB ={1,2,7,8}
2. 设U={x|x是三角形},A={x|x是锐角三角形},B={x|x是钝角三角形}.求A∩B, CU (A∪B).
解:由题意知A∩B= ,
CU(A∪B)={x|x是直角三角形}.
例1 试用集合A,B的交集、并集、补集分别表示下图中Ⅰ、Ⅱ、Ⅲ、Ⅳ四个部分所表示的集合.
U
Ⅰ
A
B
Ⅱ
Ⅲ
Ⅳ
解:Ⅰ部分:
Ⅱ部分:
Ⅲ部分:
Ⅳ部分:
例题分析
5
4
3
-1
1
0
2
6
x
5
4
1
3
-1
0
2
6
x
(3)在数轴上,画出集合CRA,CRB如图示
_________.
______________.
4.已知全集U={1,2,3,4,5,6,7},A={2,4,5},
B={1,3,5,7}求A∩(CUB),(CUA)∩ (CUB).
解:由题意可知
CUA={1,3,6,7}, CUB={2,4,6},
则A∩(CUB)={2,4},
(CUA)∩ (CUB)={6}.
若a≠1,且a≠4,a≠3,则A∪B={1,3,4,a},
A∩B= .
若a=3,则A∪B={1,3,4} ,A∩B= ,
5.设集合A={x|(x-3)(x-a)=0,a∈R},
B={x|(x-4)(x-1)=0},求A∪B,A∩B.
解:由题意可知
B={1,4}, A={a,3},
若a=1,则A∪B={1,3,4} ,A∩B={1};
若a=4,则A∪B={1,3,4} ,A∩B={4},
本节我们在集合的并、交两种基本运算的基础上学习了全集和补集的概念,在掌握概念的基础上能够熟练运用自然语言、符号语言、图形语言来表示和理解集合的全集和补集以及并集、交集的综合运算.
