2012年高一数学新课程教学课件:2.5《简单的幂函数》(北师大版必修1)
文档属性
| 名称 | 2012年高一数学新课程教学课件:2.5《简单的幂函数》(北师大版必修1) |  | |
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-05-15 13:53:42 | ||
图片预览







文档简介
(共23张PPT)
§5 简单的幂函数
1.了解指数是整数的简单幂函数的概念,会利用定义证明简单函数的奇偶性.
2.了解利用奇偶性画函数图像和研究函数的方法.
3.培养学生从特殊归纳出一般的意识.
问题引入:我们先看下面几个具体问题:
(1)如果张红买了每千克1元的蔬菜W千克,那么她需要支
付____________.
(2)如果正方形的边长为 a,那么正方形的面积___________.
(3)如果立方体的边长为a,那么立方体的体积_____________.
(4)如果正方形的面积为S,那么正方形的边长___________.
p是w的函数
S 是a的函数
V是a的函数
a是S的函数
新课引入
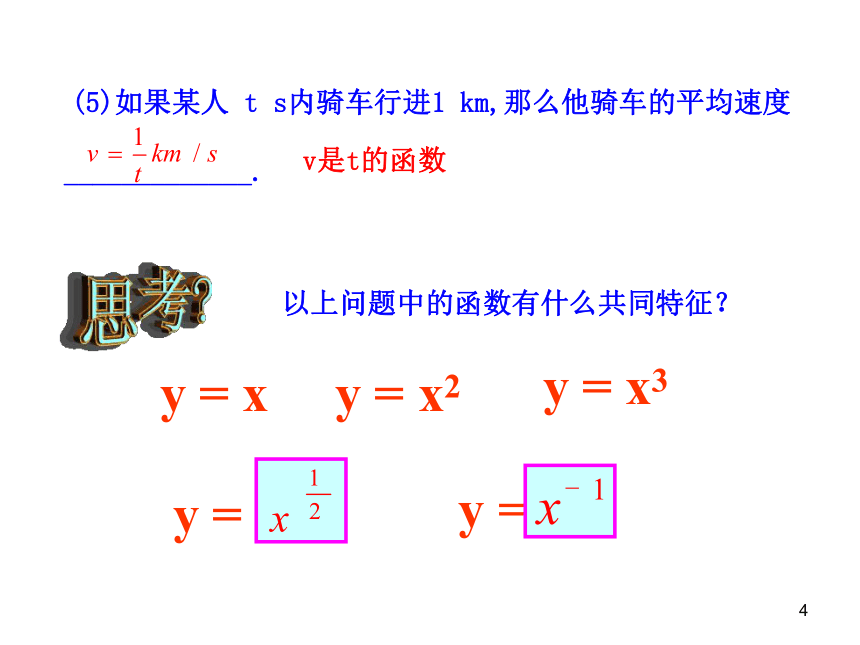
(5)如果某人 t s内骑车行进1 km,那么他骑车的平均速度
_____________.
v是t的函数
以上问题中的函数有什么共同特征?
y =
y =
y = x3
y = x
y = x2
1
x
y
o
1
-1
-1
1
x
y
o
1
-1
-1
1
x
y
o
1
-1
-1
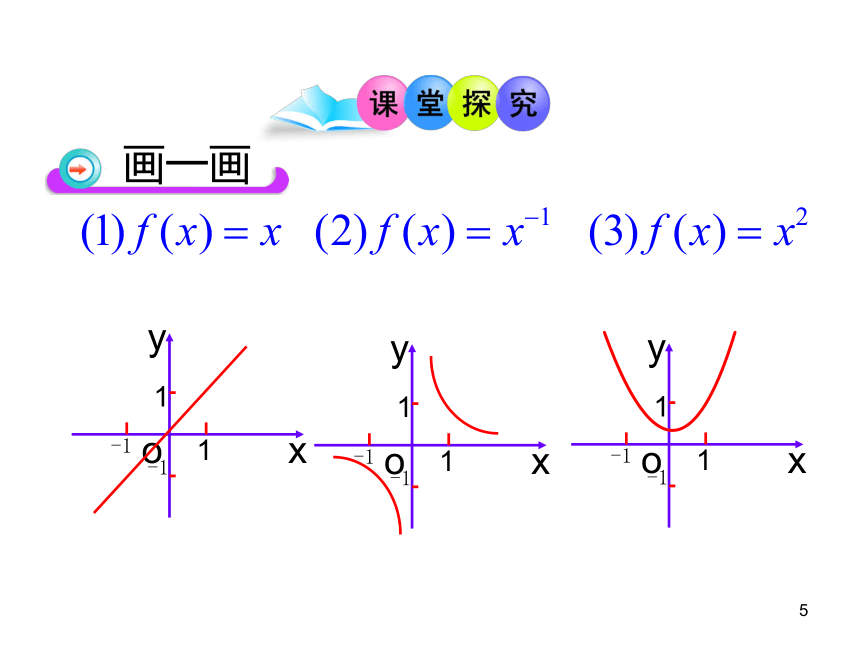
画一画
上述三个函数解析式有什么异同?
底数是自变量x,只是指数不同.
幂函数的定义:
判断下列函数是否为幂函数.
仅(3)是幂函数
判一判
画出幂函数y=x3的图像,并讨论其图像特征
(单调性、对称性等).
试一试
x … -2 -1 -1/2 0 1/2 1 2 …
y … …
-8 -1 -1/8 0 1/8 1 8
x
y
o
特征:
1.单调性:
2.对称性:
在R上是增加的.
关于原点对称
在第一象限中,幂函数的单调性
奇函数
一般地,图像关于原点对称的函数叫作奇函数.
具有的特点
偶函数
一般地,图像关于y轴对称的函数叫作偶函数.
具有的特点
例如:
1
x
y
o
1
-1
-1
y=x2
x
y
o
x
y
o
b
y=-x2
y=b
画出下列函数的图像,判断其奇偶性.
练一练
x
y
o
x
y
o
-3
3
x
y
o
-3
x
y
o
-1
1
x
y
o
1
x
y
o
1
-1
-1
-8
8
4
4
思考:
例2 判断函数f(x)=-2x5和g(x)=x4+2的奇偶性.
解: 因为在R上f(x)=-2x5
f(-x)=-2(-x)5=2x5,所以
∴ f(-x)=-f(x)
于是f(x)是奇函数.
而g(x)=x4+2 ,g(-x)=(-x)4+2= x4+2
所以 g(-x)=g(x)
于是g(x)是偶函数.
补全下面四个函数的图像
x
y
o
y=x-1
x
y
o
y=-x3
x
y
o
1
y=x2+1
x
y
o
y=-x4
1.函数f(x)=x2,x [-1,1)为偶函数.( )
2.函数y=f(x)在定义域R上是奇函数,且在(- ,0]上是增加的的,则f(x)在[0,+ )上也是增加的.( )
3.函数y=f(x)在定义域R上是偶函数,且在
(- ,0]上是减少的,则f(x)在[0,+ )上也
是减少的.( )
2.填空
(1)函数y=2x2是 函数.(填奇或偶)
(2)函数y=2x2+1是 函数.(填奇或偶)
(3)函数y=2x2+4x+1是 函数.(填奇或偶或非奇非偶)
偶
偶
非奇非偶
3.二次函数f(x)=(m-1)x2+2mx+3是偶函数,则f(x)在(- ,0]
上是( )
A.增加的 B.减少的
C.先增加后减少的 D.先减少后增加的
A
f(-2)1.几种简单幂函数的图像及性质.
2.判断函数奇偶性的方法:
(1)图像法
(2)解析法
图像关于原点对称 f(x)是奇函数.
图像关于y轴对称 f(x)是偶函数.
f(-x)=-f(x)
y=f(x)为奇函数
f(-x)=f(x)
y=f(x)为偶函数
§5 简单的幂函数
1.了解指数是整数的简单幂函数的概念,会利用定义证明简单函数的奇偶性.
2.了解利用奇偶性画函数图像和研究函数的方法.
3.培养学生从特殊归纳出一般的意识.
问题引入:我们先看下面几个具体问题:
(1)如果张红买了每千克1元的蔬菜W千克,那么她需要支
付____________.
(2)如果正方形的边长为 a,那么正方形的面积___________.
(3)如果立方体的边长为a,那么立方体的体积_____________.
(4)如果正方形的面积为S,那么正方形的边长___________.
p是w的函数
S 是a的函数
V是a的函数
a是S的函数
新课引入
(5)如果某人 t s内骑车行进1 km,那么他骑车的平均速度
_____________.
v是t的函数
以上问题中的函数有什么共同特征?
y =
y =
y = x3
y = x
y = x2
1
x
y
o
1
-1
-1
1
x
y
o
1
-1
-1
1
x
y
o
1
-1
-1
画一画
上述三个函数解析式有什么异同?
底数是自变量x,只是指数不同.
幂函数的定义:
判断下列函数是否为幂函数.
仅(3)是幂函数
判一判
画出幂函数y=x3的图像,并讨论其图像特征
(单调性、对称性等).
试一试
x … -2 -1 -1/2 0 1/2 1 2 …
y … …
-8 -1 -1/8 0 1/8 1 8
x
y
o
特征:
1.单调性:
2.对称性:
在R上是增加的.
关于原点对称
在第一象限中,幂函数的单调性
奇函数
一般地,图像关于原点对称的函数叫作奇函数.
具有的特点
偶函数
一般地,图像关于y轴对称的函数叫作偶函数.
具有的特点
例如:
1
x
y
o
1
-1
-1
y=x2
x
y
o
x
y
o
b
y=-x2
y=b
画出下列函数的图像,判断其奇偶性.
练一练
x
y
o
x
y
o
-3
3
x
y
o
-3
x
y
o
-1
1
x
y
o
1
x
y
o
1
-1
-1
-8
8
4
4
思考:
例2 判断函数f(x)=-2x5和g(x)=x4+2的奇偶性.
解: 因为在R上f(x)=-2x5
f(-x)=-2(-x)5=2x5,所以
∴ f(-x)=-f(x)
于是f(x)是奇函数.
而g(x)=x4+2 ,g(-x)=(-x)4+2= x4+2
所以 g(-x)=g(x)
于是g(x)是偶函数.
补全下面四个函数的图像
x
y
o
y=x-1
x
y
o
y=-x3
x
y
o
1
y=x2+1
x
y
o
y=-x4
1.函数f(x)=x2,x [-1,1)为偶函数.( )
2.函数y=f(x)在定义域R上是奇函数,且在(- ,0]上是增加的的,则f(x)在[0,+ )上也是增加的.( )
3.函数y=f(x)在定义域R上是偶函数,且在
(- ,0]上是减少的,则f(x)在[0,+ )上也
是减少的.( )
2.填空
(1)函数y=2x2是 函数.(填奇或偶)
(2)函数y=2x2+1是 函数.(填奇或偶)
(3)函数y=2x2+4x+1是 函数.(填奇或偶或非奇非偶)
偶
偶
非奇非偶
3.二次函数f(x)=(m-1)x2+2mx+3是偶函数,则f(x)在(- ,0]
上是( )
A.增加的 B.减少的
C.先增加后减少的 D.先减少后增加的
A
f(-2)
2.判断函数奇偶性的方法:
(1)图像法
(2)解析法
图像关于原点对称 f(x)是奇函数.
图像关于y轴对称 f(x)是偶函数.
f(-x)=-f(x)
y=f(x)为奇函数
f(-x)=f(x)
y=f(x)为偶函数
