2012年高一数学新课程教学课件:2.2.2函数的表示法(北师大版必修1)
文档属性
| 名称 | 2012年高一数学新课程教学课件:2.2.2函数的表示法(北师大版必修1) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-05-15 00:00:00 | ||
图片预览






文档简介
(共23张PPT)
2.2 函数的表示法
通过丰富的实例,体会函数的三种表示方法.
体会三种表示方法的使用情境与各自的特点.
3.通过具体实例,了解简单的分段函数,并能简单应用.
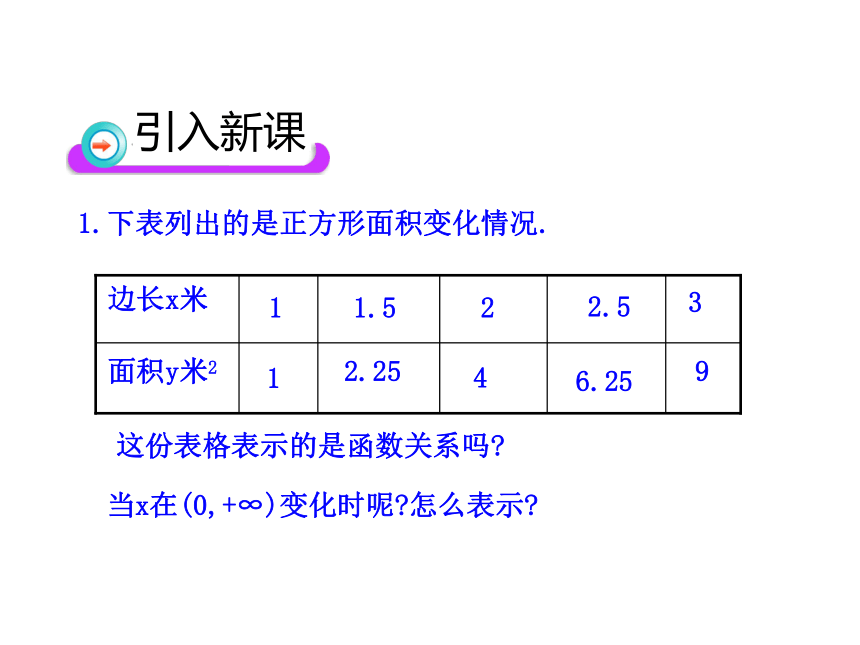
1.下表列出的是正方形面积变化情况.
这份表格表示的是函数关系吗
边长x米
面积y米2
1
1.5
2.5
2
3
1
2.25
4
6.25
9
当x在(0,+∞)变化时呢 怎么表示
引入新课
x
y
o
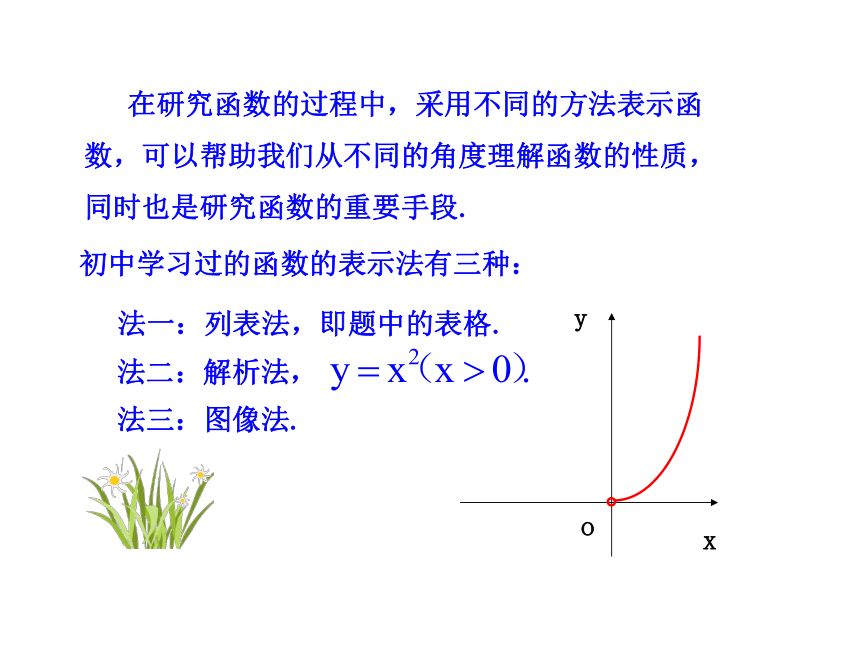
法一:列表法,即题中的表格.
法二:解析法,
法三:图像法.
初中学习过的函数的表示法有三种:
在研究函数的过程中,采用不同的方法表示函数,可以帮助我们从不同的角度理解函数的性质,同时也是研究函数的重要手段.
1.列表法
在实际问题中常常使用表格,有些表格描述了两个变量间的函数关系,比如,某天一昼夜温度变化情况如下表.
时刻 0:00 4:00 8:00 12:00 16:00 20:00 24:00
温度(℃) -2 -5 4 9 8.5 3.5 -1
像这样,用表格的形式表示两个变量之间函数关系的方法,称为列表法.
特点:列表法不用通过计算就能知道两个变量之间的对应关系,比较直观.但是,它只能表示有限个元素间的函数关系.
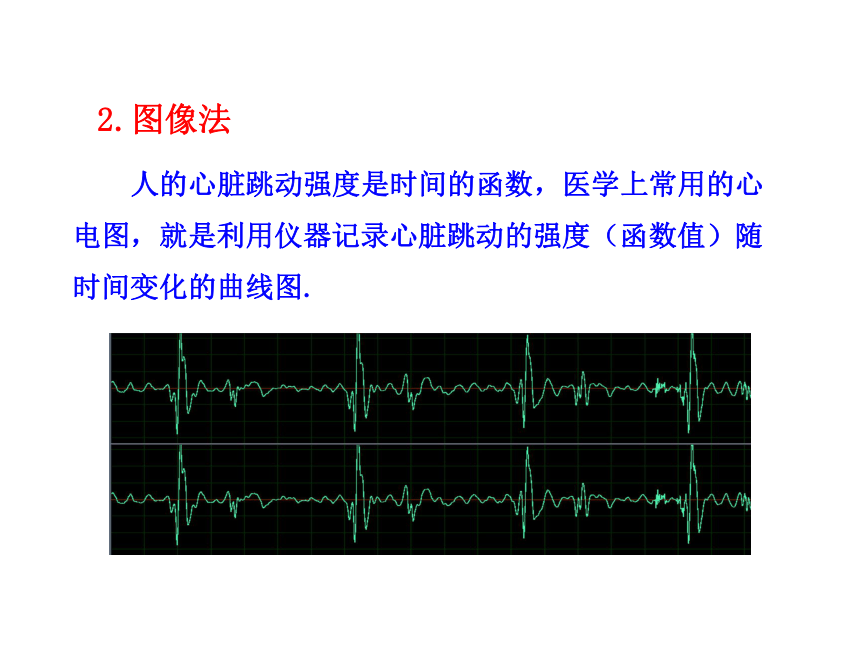
2.图像法
人的心脏跳动强度是时间的函数,医学上常用的心电图,就是利用仪器记录心脏跳动的强度(函数值)随时间变化的曲线图.
特点:图像法可以直观地表示函数的局部变化规律,进而可以预测它的整体趋势.
像这样,用图像把两个变量间的函数关系表示出来的方法,称为图像法.
3.解析法
一个函数的对应关系可以用自变量的解析表达式
(简称解析式)表示出来,这种方法称为解析法.
例如,设正方形的边长为x,面积为y,则y是x的函数,用解析式表示为
特点:解析法表示的函数关系能较便利地通过计算等手段研究函数性质.但是,一些实际问题很难找到它的解析式.
信函质量
(m)/g
邮资(M)/元 1.20 2.40 3.60 4.80 6.00
例1.国内跨省市之间邮寄信函,每封信函的质量和对应的邮资如下表:
请画出图像,并写出函数的解析式.
例题讲解
解:
邮资是信函质量的函数, 其图像如下:
m/g
1.20
2.40
3.60
4.80
6.00
20
M/元
40
60
80
100
。
。
。
。
。
O
有些函数在它的定义域中,对于自变量的不同取值范围,对应关系不同,这种函数通常称为分段函数。
1.20, 02.40, 20M= 3.60, 404.80, 606.00, 80函数解析式为
这种在定义域的不同部分,有不同的对应关系的函数称为分段函数。
1.分段函数是一个函数,不要把它误认为是“几个函数”;
2. 有些函数既可用列表法表示,也可用图像法或解析法
表示.
注意
例2.某质点在30s内运动速度v是时间t的函数,它的图像如下图.用解析法表示出
这个函数, 并求出9s时
质点的速度.
10
20
30
10
30
v cm/s
t/s
O
解: 解析式为v(t)=
t+10, t∈[0,5);
3t, t∈[5,10);
30, t∈[10,20);
由上式可得,t=9s时,质点的速度
v(9)=3×9=27 (cm/s).
-3t+90, t∈[20,30).
1.请画出函数y=|x|的图像.
解:由绝对值的定义,得
它的图像为第一和第二象限
的角平分线,如图:
x
y
-2
1
-3
0
2
3
2
3
4
5
-1
2.某种笔记本的单价是5元,买x 个笔
记本需要多少元?试用函数的三种表示法表示函数.
解:这个函数的定义域是数集{1,2,3,4,5}用解析法可将函数y=f(x)表示为
用列表法可将函数表示为
笔记本数x 1 2 3 4 5
钱数y 5 10 15 20 25
用图像法可将函数表示为下图
.
.
.
.
.
0
1
2
3
4
5
5
10
15
20
25
x
y
笔记本数x 1 2 3 4 5
钱数y 5 10 15 20 25
3.某市空调公共汽车的票价按下列规则制定:
(1)5公里以内(含5公里),票价2元;
(2)5公里以上,每增加5公里,票价增加1元(不足5 公里的按5公里计算).
已知两个相邻的公共汽车站间相距为1公里,如果沿途(包括起点站和终点站)有21个汽车站,请根据题意,写出票价与里程之间的函数解析式,并画出函数的图像.
解: 设票价为y,里程为x,则根据题意,如果某空调汽车运行路线中设21个汽车站,那么汽车行驶的里程约为20公里,所以自变量x的取值范围是(0,20]
由空调汽车票价的规定,可得到以下函数解析式:
0
5
10
15
20
1
2
3
4
5
x
y
根据函数解析式,可画出函数图像,如下图
○
○
○
○
1.掌握函数的三种表示法的优点,灵活运用三种表示法来表示函数.
2.掌握运用复合函数来表达实际问题.
3.注意灵活、准确地运用函数图像解题;
2.2 函数的表示法
通过丰富的实例,体会函数的三种表示方法.
体会三种表示方法的使用情境与各自的特点.
3.通过具体实例,了解简单的分段函数,并能简单应用.
1.下表列出的是正方形面积变化情况.
这份表格表示的是函数关系吗
边长x米
面积y米2
1
1.5
2.5
2
3
1
2.25
4
6.25
9
当x在(0,+∞)变化时呢 怎么表示
引入新课
x
y
o
法一:列表法,即题中的表格.
法二:解析法,
法三:图像法.
初中学习过的函数的表示法有三种:
在研究函数的过程中,采用不同的方法表示函数,可以帮助我们从不同的角度理解函数的性质,同时也是研究函数的重要手段.
1.列表法
在实际问题中常常使用表格,有些表格描述了两个变量间的函数关系,比如,某天一昼夜温度变化情况如下表.
时刻 0:00 4:00 8:00 12:00 16:00 20:00 24:00
温度(℃) -2 -5 4 9 8.5 3.5 -1
像这样,用表格的形式表示两个变量之间函数关系的方法,称为列表法.
特点:列表法不用通过计算就能知道两个变量之间的对应关系,比较直观.但是,它只能表示有限个元素间的函数关系.
2.图像法
人的心脏跳动强度是时间的函数,医学上常用的心电图,就是利用仪器记录心脏跳动的强度(函数值)随时间变化的曲线图.
特点:图像法可以直观地表示函数的局部变化规律,进而可以预测它的整体趋势.
像这样,用图像把两个变量间的函数关系表示出来的方法,称为图像法.
3.解析法
一个函数的对应关系可以用自变量的解析表达式
(简称解析式)表示出来,这种方法称为解析法.
例如,设正方形的边长为x,面积为y,则y是x的函数,用解析式表示为
特点:解析法表示的函数关系能较便利地通过计算等手段研究函数性质.但是,一些实际问题很难找到它的解析式.
信函质量
(m)/g
邮资(M)/元 1.20 2.40 3.60 4.80 6.00
例1.国内跨省市之间邮寄信函,每封信函的质量和对应的邮资如下表:
请画出图像,并写出函数的解析式.
例题讲解
解:
邮资是信函质量的函数, 其图像如下:
m/g
1.20
2.40
3.60
4.80
6.00
20
M/元
40
60
80
100
。
。
。
。
。
O
有些函数在它的定义域中,对于自变量的不同取值范围,对应关系不同,这种函数通常称为分段函数。
1.20, 0
这种在定义域的不同部分,有不同的对应关系的函数称为分段函数。
1.分段函数是一个函数,不要把它误认为是“几个函数”;
2. 有些函数既可用列表法表示,也可用图像法或解析法
表示.
注意
例2.某质点在30s内运动速度v是时间t的函数,它的图像如下图.用解析法表示出
这个函数, 并求出9s时
质点的速度.
10
20
30
10
30
v cm/s
t/s
O
解: 解析式为v(t)=
t+10, t∈[0,5);
3t, t∈[5,10);
30, t∈[10,20);
由上式可得,t=9s时,质点的速度
v(9)=3×9=27 (cm/s).
-3t+90, t∈[20,30).
1.请画出函数y=|x|的图像.
解:由绝对值的定义,得
它的图像为第一和第二象限
的角平分线,如图:
x
y
-2
1
-3
0
2
3
2
3
4
5
-1
2.某种笔记本的单价是5元,买x 个笔
记本需要多少元?试用函数的三种表示法表示函数.
解:这个函数的定义域是数集{1,2,3,4,5}用解析法可将函数y=f(x)表示为
用列表法可将函数表示为
笔记本数x 1 2 3 4 5
钱数y 5 10 15 20 25
用图像法可将函数表示为下图
.
.
.
.
.
0
1
2
3
4
5
5
10
15
20
25
x
y
笔记本数x 1 2 3 4 5
钱数y 5 10 15 20 25
3.某市空调公共汽车的票价按下列规则制定:
(1)5公里以内(含5公里),票价2元;
(2)5公里以上,每增加5公里,票价增加1元(不足5 公里的按5公里计算).
已知两个相邻的公共汽车站间相距为1公里,如果沿途(包括起点站和终点站)有21个汽车站,请根据题意,写出票价与里程之间的函数解析式,并画出函数的图像.
解: 设票价为y,里程为x,则根据题意,如果某空调汽车运行路线中设21个汽车站,那么汽车行驶的里程约为20公里,所以自变量x的取值范围是(0,20]
由空调汽车票价的规定,可得到以下函数解析式:
0
5
10
15
20
1
2
3
4
5
x
y
根据函数解析式,可画出函数图像,如下图
○
○
○
○
1.掌握函数的三种表示法的优点,灵活运用三种表示法来表示函数.
2.掌握运用复合函数来表达实际问题.
3.注意灵活、准确地运用函数图像解题;
