2012年高一数学新课程教学课件:3.6《指数函数、幂函数、对数函数增长的比较》(北师大版必修1)
文档属性
| 名称 | 2012年高一数学新课程教学课件:3.6《指数函数、幂函数、对数函数增长的比较》(北师大版必修1) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-05-15 00:00:00 | ||
图片预览



文档简介
(共13张PPT)
§6 指数函数、幂函数、
对数函数增长的比较
巩固幂函数、指数函数、对数函数的图象与性质。
通过比较幂函数、指数函数、对数函数的增长快慢,
了解这三种函数增速的差别。
3. 体会数形结合思想在研究图象与性质中的应用。
复习
1.幂函数
2.指数函数
3.对数函数
复习导入
如果一个函数,底数是自变量x,指数是常数 ,
1.幂函数:
这样的函数称为幂函数.
即
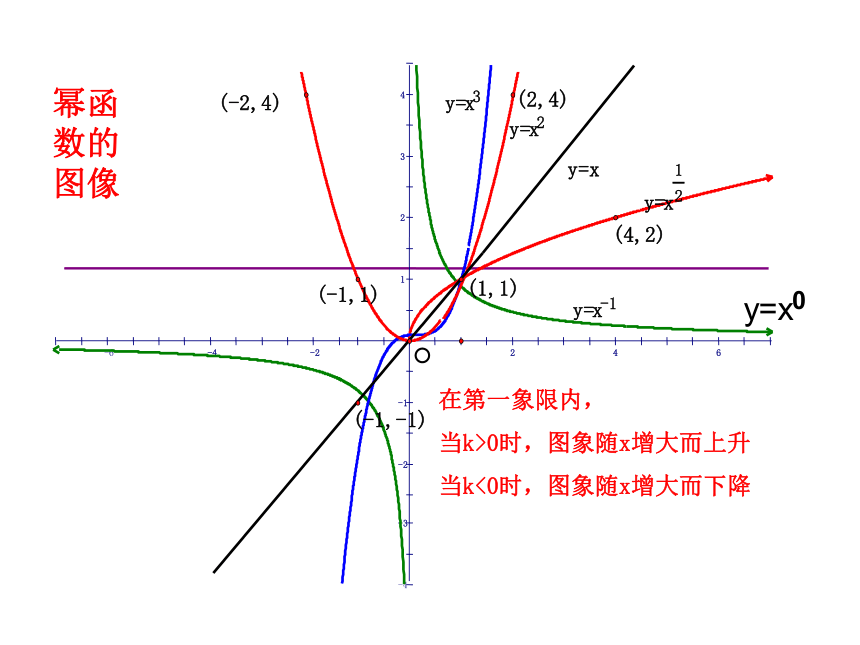
在第一象限内,
当k>0时,图象随x增大而上升
当k<0时,图象随x增大而下降
4
3
2
1
-1
-2
-3
-4
-6
-4
-2
2
4
6
y=
x
-1
y=
x
1
2
y=
x
3
y=
x
2
y=x
(4,2)
(-2,4)
(2,4)
(-1,1)
(-1,-1)
(1,1)
幂函
数的
图像
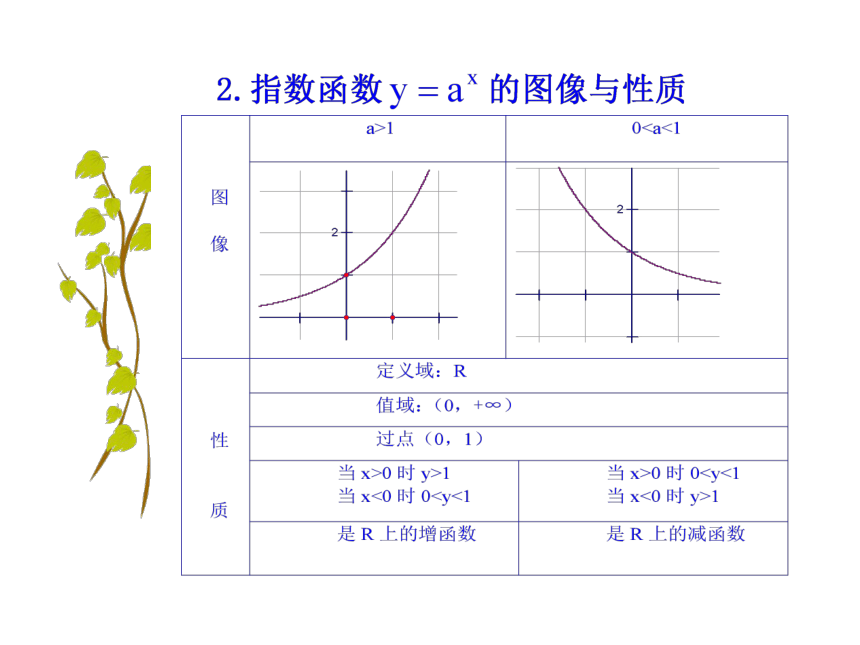
a>1 0图象
性
质 定义域:
值域:
在(0,+∞)上是
函数 在(0,+∞)上是
函数
(0,+∞)
过点(1,0),即当x=1时,y=0
增
减
0
>
y
3.对数函数
y=logax
(a>0,且
a≠1)
问题提出:
我们知道:
当a>1时,指数函数是增函数,
当a逐渐增大时,
函数值增加的越来越快;
当0 < a<1时,对数函数是减函数,
当a逐渐增大时,
函数值减少的越来越快;
当x>0时,幂函数y=xn 在(0,+∞)上单调递增;
且当x>1,n逐渐增大时,函数值增大得越来越快。
那么,对于这三种增加的函数,
它们的函数值的增加快慢有何差别呢?
我们通过三个具体的函数
y=2x,y=x100,y=㏒2x的函数值(取近似值)的比较,来体会它们的增长的快慢。
动手实践
结论:在这三个函数中,指数函数增长最快,人们常称这种现象为“指数爆炸”。
通过比较幂函数、指数函数、对数函数的增长快慢,我们要了解这三种函数增速的差别。
§6 指数函数、幂函数、
对数函数增长的比较
巩固幂函数、指数函数、对数函数的图象与性质。
通过比较幂函数、指数函数、对数函数的增长快慢,
了解这三种函数增速的差别。
3. 体会数形结合思想在研究图象与性质中的应用。
复习
1.幂函数
2.指数函数
3.对数函数
复习导入
如果一个函数,底数是自变量x,指数是常数 ,
1.幂函数:
这样的函数称为幂函数.
即
在第一象限内,
当k>0时,图象随x增大而上升
当k<0时,图象随x增大而下降
4
3
2
1
-1
-2
-3
-4
-6
-4
-2
2
4
6
y=
x
-1
y=
x
1
2
y=
x
3
y=
x
2
y=x
(4,2)
(-2,4)
(2,4)
(-1,1)
(-1,-1)
(1,1)
幂函
数的
图像
a>1 0
性
质 定义域:
值域:
在(0,+∞)上是
函数 在(0,+∞)上是
函数
(0,+∞)
过点(1,0),即当x=1时,y=0
增
减
0
>
y
3.对数函数
y=logax
(a>0,且
a≠1)
问题提出:
我们知道:
当a>1时,指数函数是增函数,
当a逐渐增大时,
函数值增加的越来越快;
当0 < a<1时,对数函数是减函数,
当a逐渐增大时,
函数值减少的越来越快;
当x>0时,幂函数y=xn 在(0,+∞)上单调递增;
且当x>1,n逐渐增大时,函数值增大得越来越快。
那么,对于这三种增加的函数,
它们的函数值的增加快慢有何差别呢?
我们通过三个具体的函数
y=2x,y=x100,y=㏒2x的函数值(取近似值)的比较,来体会它们的增长的快慢。
动手实践
结论:在这三个函数中,指数函数增长最快,人们常称这种现象为“指数爆炸”。
通过比较幂函数、指数函数、对数函数的增长快慢,我们要了解这三种函数增速的差别。
