苏科版数学九年级上册第2章 对称图形——圆2.1.1圆(21张PPT)
文档属性
| 名称 | 苏科版数学九年级上册第2章 对称图形——圆2.1.1圆(21张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-15 21:10:20 | ||
图片预览







文档简介
(共21张PPT)
Add
your
text
here
and
write
down
your
opnion
thank
you
add
your
text
here
一石激起千层浪
乐在其中
欣赏
奥运五环
福建土楼
欣赏
祥
子
小憩片刻
欣赏
车轮为什么做成圆形?
思考
线段OP绕它固定的一个端点O旋转一周,另一端点P运动所形成的图形叫做圆。
定点O叫做圆心。
线段OP叫做圆的半径。
表示:
以O为圆心的圆,记做“⊙O”,
读做“圆O”。
在同一平面内,
●
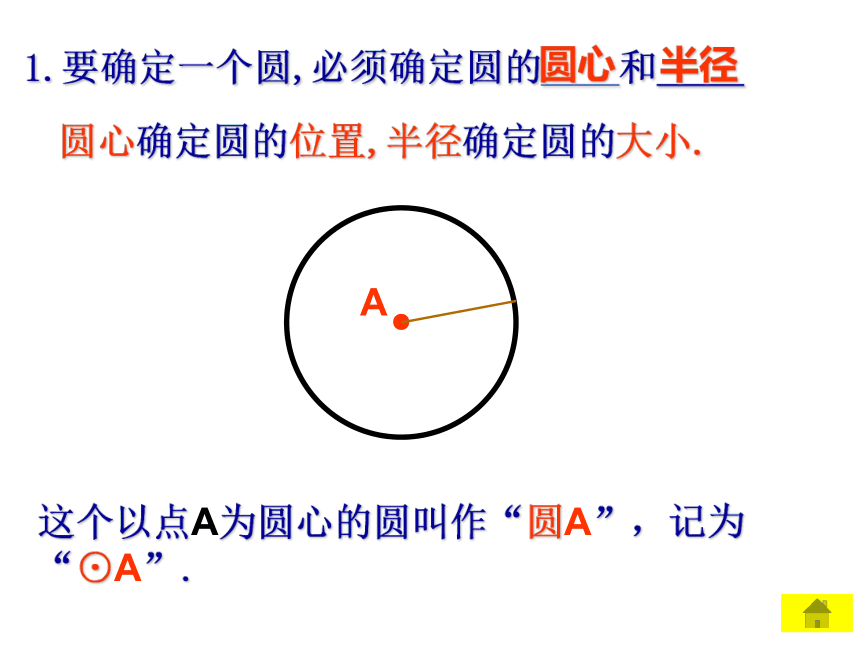
1.要确定一个圆,必须确定圆的____和____
圆心
半径
圆心确定圆的位置,半径确定圆的大小.
A
这个以点A为圆心的圆叫作“圆A”,记为“⊙A”.
爱好运动的小华、小强、小兵三人相邀搞一次掷飞镖比赛。他们把靶子钉在一面土墙上,规则是谁掷出落点离红心越近,谁就胜。如下图中A、B、C三点分别是他们三人某一轮掷镖的落点,你认为这一轮中谁的成绩好?
问题情境
A
B
C
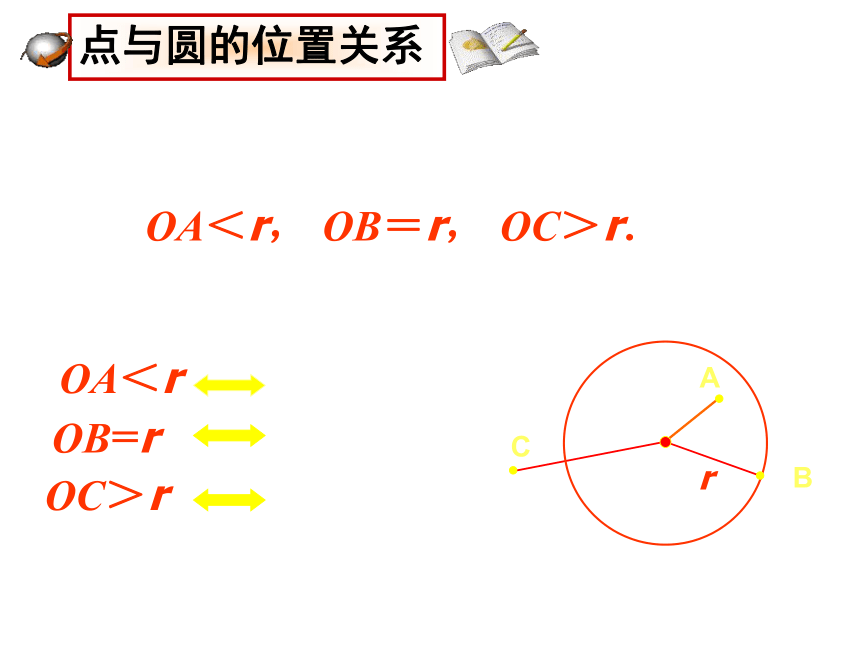
如图,设⊙O
的半径为r,A点在圆内,
B点在圆上,C点在圆外,那么
点A在⊙O内
点B在⊙O上
点C在⊙O外
OA<r,
OB=r,
OC>r.
反过来也成立,如果已知点到圆心的距离和圆的半径的关系,就可以判断点和圆的位置关系。
点与圆的位置关系
OA<r
OB=r
OC>r
A
B
C
r
o
设⊙O
的半径为r,点P到圆心的距离OP=d,则有:
点P在⊙O内
点P在⊙O上
点P在⊙O外
点与圆的位置关系
d<r
d=r
d>r
r
p
d
p
r
d
P
r
d
圆的集合定义
圆外的点
圆内的点
圆上的点
平面上的一个圆,把平面上的点分成三类:圆上的点,圆内的点和圆外的点。
圆的内部可以看成是到圆心的距离小于半径的的点的集合;圆的外部可以看成是
。
到圆心的距离大于半径的点的集合
思考:平面上的一个圆把平面上的点分成哪几部分?
圆上各点到圆心(定点)的距离都等于半径(定长);到圆心距离等于半径的点都在圆上.也就是说:
圆是到定点距离等于定长的点的集合.
总结:
圆上各点到圆心(定点)的距离都等于半径(定长);到圆心距离等于半径的点都在圆上.也就是说:圆是到定点距离等于定长的点的集合.
圆内各点到圆心的距离都小于半径;到圆心
距离小于半径的点都在圆内.也就是说:圆的内部可以看作是到圆心距离小于半径的点的集合.
圆外的点到圆心的距离都大于半径;到圆心距离大于半径的点都在圆外.也就是说:圆的外部可以看作是到圆心距离大于半径的点的集合.
角的平分线可以看成是
哪些点的集合?
线段的垂直平分线呢?
尝试与交流(动手)
如图:已知点P,Q.且PQ=4cm.
P
Q
(1)画出下列图形:到点P的距离等于2cm的点的集合;到点Q的距离等于3cm的点的集合;
(2)在所画图中,到点P的距离等于2cm,且到点Q的距离等于3cm的点有几个?请在图中将它们表示出来。
(3)在所画图中,到点P的距离小于或等于2cm,且到点Q的距离大于或等于3cm的点的集合是怎样的图形?把它画出来。
例:如图已知矩形ABCD的边AB=3厘米,AD=4厘米
典型例题
A
D
C
B
(1)以点A为圆心,3厘米为半径作圆A,则点B、C、D与圆A的位置关系如何?
(B在圆上,D在圆外,C在圆外)
(2)以点A为圆心,4厘米为半径作圆A,则点B、C、D与圆A的位置关系如何?
(B在圆内,D在圆上,C在圆外)
(3)以点A为圆心,5厘米为半径作圆A,则点B、C、D与圆A的位置关系如何?
(B在圆内,D在圆内,C在圆上)
练一练
1、⊙O的半径10cm,A、B、C三点到圆心的距离分别为8cm、10cm、12cm,则点A、B、C与⊙O的位置关系是:点A在
;点B在
;点C在
。
2、⊙O的半径6cm,当OP=6时,点A在
;
当OP
时点P在圆内;当OP
时,点P不在圆外。
3、正方形ABCD的边长为2cm,以A为圆心2cm为半径作⊙A,则点B在⊙A
;点C在⊙A
;点D在⊙A
。
圆内
圆上
圆外
圆上
<6
≤6
上
外
上
4、已知AB为⊙O的直径,P为⊙O
上任意一点,则点P关于AB的对称点P′与⊙O的位置为(
)
(A)在⊙O内
(B)在⊙O
外
(C)在⊙O
上
(D)不能确定
c
能力提高
例:
2005年9月11日,第十五号台风“卡努”登陆浙
江,A市接到台风警报时,台风中心位于A市正南方
向125km的B处,正以15km/h的速度沿BC方向移动。
已知A市到BC的距离AD=35km,如果在距离台风中
心40km(包括40km)的区域内都将受到台风影响
试问A市受到台风影响的时间是多长?
问题1:请用点与圆的位置关系描述A市何时受到台风影响?
问题2:请用点到圆心的距离和圆的半径的大小关系表示出A市何时受台风影响?
-5
-5
5
5
x
y
o
例.如图所示,P(x,y)是以坐标原点为圆心,5为半径
的圆周上的点,若x,y都是整数,问这样的点共有多少个?
坐标分别是什么?
例.
已知:如图,BD、CE是ABC的高,M是BC的中点。试问:点B、C、D、E在以点M为圆心的圆上吗?
基础例题
在同一平面内,线段OP绕它固定的一个端点O旋转一周,另一端点P
运动所形成的图形叫做圆。
要确定一个圆,必须确定圆的_圆心___和_半径___,圆心确定圆的位置,半径确定圆的大小.
点到圆心O的距离为d,那么:
点A在圆
内
d
<
r
点B在圆
上
d
=
r
点C在圆
外
d
>
r
圆是到定点距离等于定长的点的集合.
?
作业:
见当堂训练
Add
your
text
here
and
write
down
your
opnion
thank
you
add
your
text
here
一石激起千层浪
乐在其中
欣赏
奥运五环
福建土楼
欣赏
祥
子
小憩片刻
欣赏
车轮为什么做成圆形?
思考
线段OP绕它固定的一个端点O旋转一周,另一端点P运动所形成的图形叫做圆。
定点O叫做圆心。
线段OP叫做圆的半径。
表示:
以O为圆心的圆,记做“⊙O”,
读做“圆O”。
在同一平面内,
●
1.要确定一个圆,必须确定圆的____和____
圆心
半径
圆心确定圆的位置,半径确定圆的大小.
A
这个以点A为圆心的圆叫作“圆A”,记为“⊙A”.
爱好运动的小华、小强、小兵三人相邀搞一次掷飞镖比赛。他们把靶子钉在一面土墙上,规则是谁掷出落点离红心越近,谁就胜。如下图中A、B、C三点分别是他们三人某一轮掷镖的落点,你认为这一轮中谁的成绩好?
问题情境
A
B
C
如图,设⊙O
的半径为r,A点在圆内,
B点在圆上,C点在圆外,那么
点A在⊙O内
点B在⊙O上
点C在⊙O外
OA<r,
OB=r,
OC>r.
反过来也成立,如果已知点到圆心的距离和圆的半径的关系,就可以判断点和圆的位置关系。
点与圆的位置关系
OA<r
OB=r
OC>r
A
B
C
r
o
设⊙O
的半径为r,点P到圆心的距离OP=d,则有:
点P在⊙O内
点P在⊙O上
点P在⊙O外
点与圆的位置关系
d<r
d=r
d>r
r
p
d
p
r
d
P
r
d
圆的集合定义
圆外的点
圆内的点
圆上的点
平面上的一个圆,把平面上的点分成三类:圆上的点,圆内的点和圆外的点。
圆的内部可以看成是到圆心的距离小于半径的的点的集合;圆的外部可以看成是
。
到圆心的距离大于半径的点的集合
思考:平面上的一个圆把平面上的点分成哪几部分?
圆上各点到圆心(定点)的距离都等于半径(定长);到圆心距离等于半径的点都在圆上.也就是说:
圆是到定点距离等于定长的点的集合.
总结:
圆上各点到圆心(定点)的距离都等于半径(定长);到圆心距离等于半径的点都在圆上.也就是说:圆是到定点距离等于定长的点的集合.
圆内各点到圆心的距离都小于半径;到圆心
距离小于半径的点都在圆内.也就是说:圆的内部可以看作是到圆心距离小于半径的点的集合.
圆外的点到圆心的距离都大于半径;到圆心距离大于半径的点都在圆外.也就是说:圆的外部可以看作是到圆心距离大于半径的点的集合.
角的平分线可以看成是
哪些点的集合?
线段的垂直平分线呢?
尝试与交流(动手)
如图:已知点P,Q.且PQ=4cm.
P
Q
(1)画出下列图形:到点P的距离等于2cm的点的集合;到点Q的距离等于3cm的点的集合;
(2)在所画图中,到点P的距离等于2cm,且到点Q的距离等于3cm的点有几个?请在图中将它们表示出来。
(3)在所画图中,到点P的距离小于或等于2cm,且到点Q的距离大于或等于3cm的点的集合是怎样的图形?把它画出来。
例:如图已知矩形ABCD的边AB=3厘米,AD=4厘米
典型例题
A
D
C
B
(1)以点A为圆心,3厘米为半径作圆A,则点B、C、D与圆A的位置关系如何?
(B在圆上,D在圆外,C在圆外)
(2)以点A为圆心,4厘米为半径作圆A,则点B、C、D与圆A的位置关系如何?
(B在圆内,D在圆上,C在圆外)
(3)以点A为圆心,5厘米为半径作圆A,则点B、C、D与圆A的位置关系如何?
(B在圆内,D在圆内,C在圆上)
练一练
1、⊙O的半径10cm,A、B、C三点到圆心的距离分别为8cm、10cm、12cm,则点A、B、C与⊙O的位置关系是:点A在
;点B在
;点C在
。
2、⊙O的半径6cm,当OP=6时,点A在
;
当OP
时点P在圆内;当OP
时,点P不在圆外。
3、正方形ABCD的边长为2cm,以A为圆心2cm为半径作⊙A,则点B在⊙A
;点C在⊙A
;点D在⊙A
。
圆内
圆上
圆外
圆上
<6
≤6
上
外
上
4、已知AB为⊙O的直径,P为⊙O
上任意一点,则点P关于AB的对称点P′与⊙O的位置为(
)
(A)在⊙O内
(B)在⊙O
外
(C)在⊙O
上
(D)不能确定
c
能力提高
例:
2005年9月11日,第十五号台风“卡努”登陆浙
江,A市接到台风警报时,台风中心位于A市正南方
向125km的B处,正以15km/h的速度沿BC方向移动。
已知A市到BC的距离AD=35km,如果在距离台风中
心40km(包括40km)的区域内都将受到台风影响
试问A市受到台风影响的时间是多长?
问题1:请用点与圆的位置关系描述A市何时受到台风影响?
问题2:请用点到圆心的距离和圆的半径的大小关系表示出A市何时受台风影响?
-5
-5
5
5
x
y
o
例.如图所示,P(x,y)是以坐标原点为圆心,5为半径
的圆周上的点,若x,y都是整数,问这样的点共有多少个?
坐标分别是什么?
例.
已知:如图,BD、CE是ABC的高,M是BC的中点。试问:点B、C、D、E在以点M为圆心的圆上吗?
基础例题
在同一平面内,线段OP绕它固定的一个端点O旋转一周,另一端点P
运动所形成的图形叫做圆。
要确定一个圆,必须确定圆的_圆心___和_半径___,圆心确定圆的位置,半径确定圆的大小.
点到圆心O的距离为d,那么:
点A在圆
内
d
<
r
点B在圆
上
d
=
r
点C在圆
外
d
>
r
圆是到定点距离等于定长的点的集合.
?
作业:
见当堂训练
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
