山东省烟台招远市(五四制)2020-2021学年六年级下学期期末考试数学试题(word版 含答案)
文档属性
| 名称 | 山东省烟台招远市(五四制)2020-2021学年六年级下学期期末考试数学试题(word版 含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 910.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-15 00:00:00 | ||
图片预览




文档简介
绝密★启用前
2020-2021学年度第二学期期末考试
初一数学试卷
说明:1. 考试时间120分钟,满分120分。
2. 考试过程允许学生进行剪、拼、折叠等实验。
一.选择题(本大题共12个小题,每小题3分,满分36分)
1.如图所示,某同学的家在P处,他想尽快赶到附近公路边搭顺风车,他选择P→C路线,用几何知识解释其道理正确的是( )
A.两点确定一条直线 B.垂线段最短
C.两点之间线段最短 D.经过一点有无数条直线
2.给出下列计算,其中正确的是( )
A.a5+a5=a10 B.(2a2)3=6a6 C.a8÷a2=a4 D.(a3)4=a12
3.为了了解某校六年级1000名学生期中数学考试情况,从中抽取了80名学生的数学成绩进行了统计,下面4个判断中正确的有( )个.
①这种调查的方式是抽样调查;
②1000名学生是总体;
③每名学生的数学成绩是个体;
④80名学生是总体的一个样本;
A.1 B.2 C.3 D.4
4.如图,一个长方形推拉窗,窗高1.4m,当活动窗扇沿图中所示的方向移动时,随着窗扇拉开长度b (m)的变化,窗户的通风面积A (m2) 也发生了变化。在这个变化过程中,当拉开长度b从0.1m变化到0.4m时,通风面积A从_ m2变化到___ m2. ( )
A.0.14 5.6 B.0.24 0.48 C.0.14 0.56 D.2.4 5.6
.
5.如图,把一块直角三角尺的直角顶点放在直尺的一边上,若∠1=58°,则∠2的度数为( )
A.32° B.42° C.52° D.58°
6.为了了解本校六年级学生的体能情况,随机抽查了其中30名学生,测试了1分钟仰卧起坐的次数,并绘制成如图所示的频数分布直方图(每组数据包含最小值,不包含最大值),则仰卧起坐次数在25次(含25次)以上的人数共有( )
A.22人 B.17人 C.12人 D.都不对
7.若10x=10,10y= ,则x,y之间的关系为( )
A.x,y互为相反数 B.x,y互为倒数
C.x=y D.无法判断
8.研究表明,当每公顷钾肥和磷肥的施用量一定时,氮肥施用量与土豆的产量有如表所示的关系:
氮肥施用量/千克 0 34 67 101 135 202 259 336 404 471
土豆产量/吨 15.18 21.36 25.72 32.29 34.05 39.45 43.15 43.46 40.83 30.75
下列说法错误的是( )
A.氮肥施用量是自变量,土豆产量是因变量
B.当氮肥的施用量是202千克/公顷时,土豆的产量是39.45吨/公顷
C.如果不施氮肥,土豆的产量是15.18吨/公顷
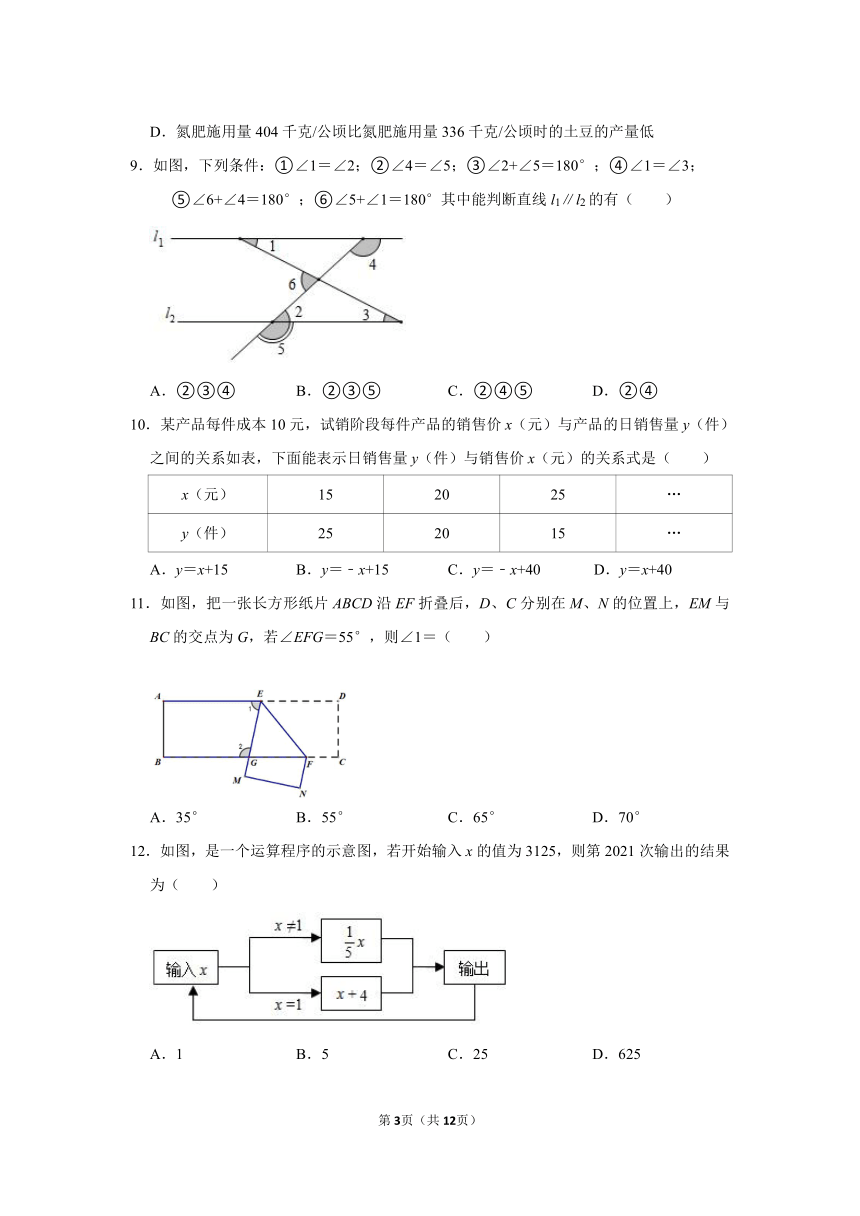
D.氮肥施用量404千克/公顷比氮肥施用量336千克/公顷时的土豆的产量低
9.如图,下列条件:①∠1=∠2;②∠4=∠5;③∠2+∠5=180°;④∠1=∠3;
⑤∠6+∠4=180°;⑥∠5+∠1=180°其中能判断直线l1∥l2的有( )
A.②③④ B.②③⑤ C.②④⑤ D.②④
10.某产品每件成本10元,试销阶段每件产品的销售价x(元)与产品的日销售量y(件)之间的关系如表,下面能表示日销售量y(件)与销售价x(元)的关系式是( )
x(元) 15 20 25 …
y(件) 25 20 15 …
A.y=x+15 B.y=﹣x+15 C.y=﹣x+40 D.y=x+40
11.如图,把一张长方形纸片ABCD沿EF折叠后,D、C分别在M、N的位置上,EM与BC的交点为G,若∠EFG=55°,则∠1=( )
A.35° B.55° C.65° D.70°
12.如图,是一个运算程序的示意图,若开始输入x的值为3125,则第2021次输出的结果为( )
A.1 B.5 C.25 D.625
二.填空题(本大题共6个小题,每小题3分,满分18分)
13.检查一批袋装食品中防腐剂的含量,宜采用的调查方式是 . (选填“普查”或“抽样调查”)
14.如图是一,二两组同学将本组最近5次数学平均成绩.分别绘制成的折线统计图.由统计图可知 组进步更大.(选填“一“或“二”)
15.如图,将一副三角尺按不同的位置摆放,下列摆放方式中,∠α与∠β互余的是
16.如图,在长方形ABCD中,动点P从A出发,以相同的速度,沿A→B→C→D→A方向运动到点A处停止.设点P运动的路程为x,△PCD的面积为y,如果y与x之间的关系如图所示,那么长方形ABCD的面积为 (图中6和16改为7和17)
17.如图,已知AB∥CD,∠ABE和∠CDE的平分线相交于F,∠BED=110°,则∠BFD的度数为
18.如图,下列每个三角形中的三个数之间均具有相同的规律,按此规律,最后一个三角形中y与x之间关系的表达式是 .
三.解答题(第19、20、21、22题各8分,第23题10分,第24题11分,第25题13分)
19.计算
(1)103×97(利用乘法公式计算)
(2)先化简,再求值:(3a5b3+a4b2)÷(﹣a2b)2﹣(2+a)(2﹣a)﹣(a﹣b)2,其中a=﹣,b=2.
20.请将下列题目的证明过程补充完整,将答案填写在横线处:
如图,F是BC上一点,FG⊥AC于点G,H是AB上一点,HE⊥AC于点E,∠1=∠2,求证:DE∥BC.
证明:连接EF.
因为FG⊥AC,HE⊥AC,
所以∠FGC=∠HEC=90°.
所以FG∥ ① ( ② ).
∴∠3= ③ ( ④ ).
又∵∠1=∠2,
∴ ⑤ = ⑥ ,
即 ⑦ =∠EFC.
∴DE∥BC( ⑧ ).
21.我省有关部门要求各中小学要把“阳光体育”写入课表,为了响应这一号召,某校围绕着“你最喜欢的体育活动项目是什么?(只写一项)”的问题,对在校学生进行了随机抽样调查,从而得到一组数据,如图1是根据这组数据绘制的条形统计图,请结合统计图回答下列问题:
(1)该校对多少名学生进行了抽样调查?
(2)本次抽样调查中,最喜欢足球活动的有多少人?占被调查人数的百分比是多少?
(3)若该校九年级共有300名学生,图2是根据各年级学生人数占全校学生总人数的百分比绘制的扇形统计图,请你估计全校学生中最喜欢篮球活动的人数约为多少?
22.如图,直线AB,CD交于点O,将一个三角板的直角顶点放置于点O处,使其两条直角边分别位于OC的两侧.若OC刚好平分∠BOF,∠BOE=2∠COE,求∠COE的度数.
23.飞机飞行跟海拔高度和相应高度处气温有密切的联系。下面表格是某处当日海拔高度h(千米)与相应高度处气温t(℃)的关系:
海拔高度h(千米) 0 1 2 3 4 5 …
气温t(℃) 20 14 8 2 ﹣4 ﹣10 …
根据上表,回答以下问题:
(1)由上表可知海拔5千米的上空气温约为 ℃;
某日飞机在航行过程中玻璃爆裂,立刻降落。飞机下降过程中海拔高度与玻璃爆裂后立即返回地面所用的时间关系图如下.根据图象回答以下问题:
(2)挡风玻璃在高空爆裂时飞机所处的高度为 千米,返回地面用了 分钟;飞机在2千米高空水平面上大约盘旋了 分钟;
(3)挡风玻璃在高空爆裂时,当时飞机所处高空的气温为多少?
24.问题情境
在综合与实践课上,老师让同学们以“两条平行线AB,CD和一块含60°角的直角三角尺EFG(∠EFG=90°,∠EGF=60°)”为主题开展数学活动.
操作发现
(1)如图(1),小明把三角尺的60°角的顶点G放在CD上,若∠2=∠1,求∠1的度数;
(2)如图(2),小颖把三角尺的两个锐角的顶点E、G分别放在AB和CD上,请你探索并说明∠AEF与∠FGC之间的数量关系;
结论应用
(3)如图(3),小亮把三角尺的直角顶点F放在CD上,30°角的顶点E落在AB上.若∠AEG=α,则∠CFG等于 (用含α的式子表示).
25.小明和小华是姐弟俩,某日早晨,小明7:40先从家出发去学校,走了一段后,在途中广场看到志愿者们在向过往行人讲解卫生防疫常识,小明想起自己在学校学到的卫生防疫常识,于是停下来加入了志愿者队伍,后来发现上课时间快到了,就开始跑步上学,恰好在8:00赶到学校;小华离家后沿着与小明同一条道路前往学校,速度一直保持不变,也恰好在8:00赶到学校,他们从家到学校已走的路程s(米)和所用时间t(分钟)的关系图如图所示,请结合图中信息解答下列问题:
(1)小明家和学校的距离是 米;小明在广场向行人讲解卫生防疫常识所用的时间是 分钟;小华到校所用的时间是 分钟
(2)分别求小华的速度和小明从广场跑去学校的速度;
(3)求小华在广场看到小明时是几点几分?
(4)如果小明在广场进行卫生防疫常识讲解后,继续以之前的速度去往学校,假设讲解1次卫生防疫常识需要1分钟,在保证不迟到(不超过8:00)的情况下,通过计算求小明最多可以讲解几次?(结果保留整数)
2020—2021学年度第二学期期末考试
初一数学参考答案及评分意见
一.选择题(本大题共12个小题,每小题3分,满分36分)
1.B 2.D 3.B 4.C 5.A 6.B 7.A 8.A 9.D 10.C 11.D 12. A
二.填空题(本大题共6个小题,每小题3分,满分18分)
13抽样调查 14.“一” 15.图① 16. 21 17. 125? 18.y=x+2x-1
解答题(第19、20、21、23题各8分,第22题10分,第24、25题12分)
19.计算
(1) 103×97
=(100+3)×(100﹣3)
=1002﹣32
=10000﹣9
=9991. ...............................................................3分
(2)(3a5b3+a4b2)÷(﹣a2b)2﹣(2+a)(2﹣a)﹣(a﹣b)2
=(3a5b3+a4b2)÷a4b2﹣(4﹣a2)﹣(a2﹣2ab+b2)
=3ab+1﹣4+a2﹣a2+2ab﹣b2
=5ab﹣b2﹣3, ...............................................................6分
当,b=2时,
原式==﹣9................................................................8分
① HE ...............................................................1分
② 同位角相等,两直线平行 ...............................................................2分
③ ∠4 ...............................................................3分
④ 两直线平行,内错角相等 ...............................................................4分
⑤ ∠1+∠3 ...............................................................5分
⑥ ∠2+∠4, ...............................................................6分
⑦ ∠ DEF ...............................................................7分
⑧ 内错角相等,两直线平行 . ..............................................................8分
21.解:(1)4﹢8﹢10﹢18﹢10=50(名)
答:该校对50名学生进行了抽样调查..............................................2分
(2)最喜欢足球活动的有10人,占被调查人数的20%.....................................4分
(3)全校学生人数:300÷(1﹣30%﹣24%﹣26%)
=300÷20%
=1500(人)
则全校学生中最喜欢篮球活动的人数约为1500×=540(人)........8分
22.解:设∠COE=α,
由于已知∠BOE=2∠COE,
所以∠BOE=2α, ...............................................................2分
所以∠BOC=∠BOE+∠COE=2α+α=3α, ..................................................4分
因为OC平分∠BOF,根据角平分线的定义,
所以∠BOC=∠FOC=3α, ...............................................................5分
因为∠EOF是直角,
所以∠EOF=90°,
所以∠EOF=∠FOC+∠COE=3α+α=4α=90°,.......................................8分
所以α=22.5°, .......................................9分
即∠COE=22.5°. .......................................10分
解:(1)﹣10; .......................................2分
(2)9,20,2 .......................................5分
(3)当h=9时,t=20﹣6×9=﹣34(℃),
答:气温为﹣34℃.......................................8分
24.
解:(1)如图1,因为AB∥CD,
所以∠1=∠EGD,
又因为∠2=∠1,
所以∠2=∠EGD, .......................................2分
又因为∠FGE=60°,
所以∠EGD+∠2=180°﹣∠FGE,
所以∠EGD=(180°﹣60°)=60°,
所以∠1=60°; .......................................4分
(2)如图2,因为AB∥CD,
所以∠AEG+∠CGE=180°,
即∠AEF+∠FEG+∠EGF+∠FGC=180°, .......................................6分
因为∠F=90°
所以∠FEG+∠EGF=90°,
所以∠AEF+∠FGC=90°; .......................................8分
(3)如图3,因为AB∥CD,
所以∠AEF+∠CFE=180°,
即∠AEG+∠FEG+∠EFG+∠GFC=180°, .......................................10分
又因为∠GFE=90°,∠GEF=30°,∠AEG=α,
∴∠GFC=180°﹣90°﹣30°﹣α=60°﹣α. .......................................12分
25.解:(1)1280;6;16 .......................................3分
(2)小华的速度为:1280÷(20﹣4)=80(米/分),
小明从广场跑去学校的速度为:(1280﹣560)÷(20﹣14)=120(米/分);
.......................................5分
(3)560÷80=7(分),40+4+7=51(分),
答:小华在广场看到小明时是7:51;
.......................................8分
(4)1280÷(560÷8)=(分),
20﹣=(分),
,
答:在保证不迟到的情况下,小明最多可以讲解1次.
.......................................12分
第1页(共1页)
2020-2021学年度第二学期期末考试
初一数学试卷
说明:1. 考试时间120分钟,满分120分。
2. 考试过程允许学生进行剪、拼、折叠等实验。
一.选择题(本大题共12个小题,每小题3分,满分36分)
1.如图所示,某同学的家在P处,他想尽快赶到附近公路边搭顺风车,他选择P→C路线,用几何知识解释其道理正确的是( )
A.两点确定一条直线 B.垂线段最短
C.两点之间线段最短 D.经过一点有无数条直线
2.给出下列计算,其中正确的是( )
A.a5+a5=a10 B.(2a2)3=6a6 C.a8÷a2=a4 D.(a3)4=a12
3.为了了解某校六年级1000名学生期中数学考试情况,从中抽取了80名学生的数学成绩进行了统计,下面4个判断中正确的有( )个.
①这种调查的方式是抽样调查;
②1000名学生是总体;
③每名学生的数学成绩是个体;
④80名学生是总体的一个样本;
A.1 B.2 C.3 D.4
4.如图,一个长方形推拉窗,窗高1.4m,当活动窗扇沿图中所示的方向移动时,随着窗扇拉开长度b (m)的变化,窗户的通风面积A (m2) 也发生了变化。在这个变化过程中,当拉开长度b从0.1m变化到0.4m时,通风面积A从_ m2变化到___ m2. ( )
A.0.14 5.6 B.0.24 0.48 C.0.14 0.56 D.2.4 5.6
.
5.如图,把一块直角三角尺的直角顶点放在直尺的一边上,若∠1=58°,则∠2的度数为( )
A.32° B.42° C.52° D.58°
6.为了了解本校六年级学生的体能情况,随机抽查了其中30名学生,测试了1分钟仰卧起坐的次数,并绘制成如图所示的频数分布直方图(每组数据包含最小值,不包含最大值),则仰卧起坐次数在25次(含25次)以上的人数共有( )
A.22人 B.17人 C.12人 D.都不对
7.若10x=10,10y= ,则x,y之间的关系为( )
A.x,y互为相反数 B.x,y互为倒数
C.x=y D.无法判断
8.研究表明,当每公顷钾肥和磷肥的施用量一定时,氮肥施用量与土豆的产量有如表所示的关系:
氮肥施用量/千克 0 34 67 101 135 202 259 336 404 471
土豆产量/吨 15.18 21.36 25.72 32.29 34.05 39.45 43.15 43.46 40.83 30.75
下列说法错误的是( )
A.氮肥施用量是自变量,土豆产量是因变量
B.当氮肥的施用量是202千克/公顷时,土豆的产量是39.45吨/公顷
C.如果不施氮肥,土豆的产量是15.18吨/公顷
D.氮肥施用量404千克/公顷比氮肥施用量336千克/公顷时的土豆的产量低
9.如图,下列条件:①∠1=∠2;②∠4=∠5;③∠2+∠5=180°;④∠1=∠3;
⑤∠6+∠4=180°;⑥∠5+∠1=180°其中能判断直线l1∥l2的有( )
A.②③④ B.②③⑤ C.②④⑤ D.②④
10.某产品每件成本10元,试销阶段每件产品的销售价x(元)与产品的日销售量y(件)之间的关系如表,下面能表示日销售量y(件)与销售价x(元)的关系式是( )
x(元) 15 20 25 …
y(件) 25 20 15 …
A.y=x+15 B.y=﹣x+15 C.y=﹣x+40 D.y=x+40
11.如图,把一张长方形纸片ABCD沿EF折叠后,D、C分别在M、N的位置上,EM与BC的交点为G,若∠EFG=55°,则∠1=( )
A.35° B.55° C.65° D.70°
12.如图,是一个运算程序的示意图,若开始输入x的值为3125,则第2021次输出的结果为( )
A.1 B.5 C.25 D.625
二.填空题(本大题共6个小题,每小题3分,满分18分)
13.检查一批袋装食品中防腐剂的含量,宜采用的调查方式是 . (选填“普查”或“抽样调查”)
14.如图是一,二两组同学将本组最近5次数学平均成绩.分别绘制成的折线统计图.由统计图可知 组进步更大.(选填“一“或“二”)
15.如图,将一副三角尺按不同的位置摆放,下列摆放方式中,∠α与∠β互余的是
16.如图,在长方形ABCD中,动点P从A出发,以相同的速度,沿A→B→C→D→A方向运动到点A处停止.设点P运动的路程为x,△PCD的面积为y,如果y与x之间的关系如图所示,那么长方形ABCD的面积为 (图中6和16改为7和17)
17.如图,已知AB∥CD,∠ABE和∠CDE的平分线相交于F,∠BED=110°,则∠BFD的度数为
18.如图,下列每个三角形中的三个数之间均具有相同的规律,按此规律,最后一个三角形中y与x之间关系的表达式是 .
三.解答题(第19、20、21、22题各8分,第23题10分,第24题11分,第25题13分)
19.计算
(1)103×97(利用乘法公式计算)
(2)先化简,再求值:(3a5b3+a4b2)÷(﹣a2b)2﹣(2+a)(2﹣a)﹣(a﹣b)2,其中a=﹣,b=2.
20.请将下列题目的证明过程补充完整,将答案填写在横线处:
如图,F是BC上一点,FG⊥AC于点G,H是AB上一点,HE⊥AC于点E,∠1=∠2,求证:DE∥BC.
证明:连接EF.
因为FG⊥AC,HE⊥AC,
所以∠FGC=∠HEC=90°.
所以FG∥ ① ( ② ).
∴∠3= ③ ( ④ ).
又∵∠1=∠2,
∴ ⑤ = ⑥ ,
即 ⑦ =∠EFC.
∴DE∥BC( ⑧ ).
21.我省有关部门要求各中小学要把“阳光体育”写入课表,为了响应这一号召,某校围绕着“你最喜欢的体育活动项目是什么?(只写一项)”的问题,对在校学生进行了随机抽样调查,从而得到一组数据,如图1是根据这组数据绘制的条形统计图,请结合统计图回答下列问题:
(1)该校对多少名学生进行了抽样调查?
(2)本次抽样调查中,最喜欢足球活动的有多少人?占被调查人数的百分比是多少?
(3)若该校九年级共有300名学生,图2是根据各年级学生人数占全校学生总人数的百分比绘制的扇形统计图,请你估计全校学生中最喜欢篮球活动的人数约为多少?
22.如图,直线AB,CD交于点O,将一个三角板的直角顶点放置于点O处,使其两条直角边分别位于OC的两侧.若OC刚好平分∠BOF,∠BOE=2∠COE,求∠COE的度数.
23.飞机飞行跟海拔高度和相应高度处气温有密切的联系。下面表格是某处当日海拔高度h(千米)与相应高度处气温t(℃)的关系:
海拔高度h(千米) 0 1 2 3 4 5 …
气温t(℃) 20 14 8 2 ﹣4 ﹣10 …
根据上表,回答以下问题:
(1)由上表可知海拔5千米的上空气温约为 ℃;
某日飞机在航行过程中玻璃爆裂,立刻降落。飞机下降过程中海拔高度与玻璃爆裂后立即返回地面所用的时间关系图如下.根据图象回答以下问题:
(2)挡风玻璃在高空爆裂时飞机所处的高度为 千米,返回地面用了 分钟;飞机在2千米高空水平面上大约盘旋了 分钟;
(3)挡风玻璃在高空爆裂时,当时飞机所处高空的气温为多少?
24.问题情境
在综合与实践课上,老师让同学们以“两条平行线AB,CD和一块含60°角的直角三角尺EFG(∠EFG=90°,∠EGF=60°)”为主题开展数学活动.
操作发现
(1)如图(1),小明把三角尺的60°角的顶点G放在CD上,若∠2=∠1,求∠1的度数;
(2)如图(2),小颖把三角尺的两个锐角的顶点E、G分别放在AB和CD上,请你探索并说明∠AEF与∠FGC之间的数量关系;
结论应用
(3)如图(3),小亮把三角尺的直角顶点F放在CD上,30°角的顶点E落在AB上.若∠AEG=α,则∠CFG等于 (用含α的式子表示).
25.小明和小华是姐弟俩,某日早晨,小明7:40先从家出发去学校,走了一段后,在途中广场看到志愿者们在向过往行人讲解卫生防疫常识,小明想起自己在学校学到的卫生防疫常识,于是停下来加入了志愿者队伍,后来发现上课时间快到了,就开始跑步上学,恰好在8:00赶到学校;小华离家后沿着与小明同一条道路前往学校,速度一直保持不变,也恰好在8:00赶到学校,他们从家到学校已走的路程s(米)和所用时间t(分钟)的关系图如图所示,请结合图中信息解答下列问题:
(1)小明家和学校的距离是 米;小明在广场向行人讲解卫生防疫常识所用的时间是 分钟;小华到校所用的时间是 分钟
(2)分别求小华的速度和小明从广场跑去学校的速度;
(3)求小华在广场看到小明时是几点几分?
(4)如果小明在广场进行卫生防疫常识讲解后,继续以之前的速度去往学校,假设讲解1次卫生防疫常识需要1分钟,在保证不迟到(不超过8:00)的情况下,通过计算求小明最多可以讲解几次?(结果保留整数)
2020—2021学年度第二学期期末考试
初一数学参考答案及评分意见
一.选择题(本大题共12个小题,每小题3分,满分36分)
1.B 2.D 3.B 4.C 5.A 6.B 7.A 8.A 9.D 10.C 11.D 12. A
二.填空题(本大题共6个小题,每小题3分,满分18分)
13抽样调查 14.“一” 15.图① 16. 21 17. 125? 18.y=x+2x-1
解答题(第19、20、21、23题各8分,第22题10分,第24、25题12分)
19.计算
(1) 103×97
=(100+3)×(100﹣3)
=1002﹣32
=10000﹣9
=9991. ...............................................................3分
(2)(3a5b3+a4b2)÷(﹣a2b)2﹣(2+a)(2﹣a)﹣(a﹣b)2
=(3a5b3+a4b2)÷a4b2﹣(4﹣a2)﹣(a2﹣2ab+b2)
=3ab+1﹣4+a2﹣a2+2ab﹣b2
=5ab﹣b2﹣3, ...............................................................6分
当,b=2时,
原式==﹣9................................................................8分
① HE ...............................................................1分
② 同位角相等,两直线平行 ...............................................................2分
③ ∠4 ...............................................................3分
④ 两直线平行,内错角相等 ...............................................................4分
⑤ ∠1+∠3 ...............................................................5分
⑥ ∠2+∠4, ...............................................................6分
⑦ ∠ DEF ...............................................................7分
⑧ 内错角相等,两直线平行 . ..............................................................8分
21.解:(1)4﹢8﹢10﹢18﹢10=50(名)
答:该校对50名学生进行了抽样调查..............................................2分
(2)最喜欢足球活动的有10人,占被调查人数的20%.....................................4分
(3)全校学生人数:300÷(1﹣30%﹣24%﹣26%)
=300÷20%
=1500(人)
则全校学生中最喜欢篮球活动的人数约为1500×=540(人)........8分
22.解:设∠COE=α,
由于已知∠BOE=2∠COE,
所以∠BOE=2α, ...............................................................2分
所以∠BOC=∠BOE+∠COE=2α+α=3α, ..................................................4分
因为OC平分∠BOF,根据角平分线的定义,
所以∠BOC=∠FOC=3α, ...............................................................5分
因为∠EOF是直角,
所以∠EOF=90°,
所以∠EOF=∠FOC+∠COE=3α+α=4α=90°,.......................................8分
所以α=22.5°, .......................................9分
即∠COE=22.5°. .......................................10分
解:(1)﹣10; .......................................2分
(2)9,20,2 .......................................5分
(3)当h=9时,t=20﹣6×9=﹣34(℃),
答:气温为﹣34℃.......................................8分
24.
解:(1)如图1,因为AB∥CD,
所以∠1=∠EGD,
又因为∠2=∠1,
所以∠2=∠EGD, .......................................2分
又因为∠FGE=60°,
所以∠EGD+∠2=180°﹣∠FGE,
所以∠EGD=(180°﹣60°)=60°,
所以∠1=60°; .......................................4分
(2)如图2,因为AB∥CD,
所以∠AEG+∠CGE=180°,
即∠AEF+∠FEG+∠EGF+∠FGC=180°, .......................................6分
因为∠F=90°
所以∠FEG+∠EGF=90°,
所以∠AEF+∠FGC=90°; .......................................8分
(3)如图3,因为AB∥CD,
所以∠AEF+∠CFE=180°,
即∠AEG+∠FEG+∠EFG+∠GFC=180°, .......................................10分
又因为∠GFE=90°,∠GEF=30°,∠AEG=α,
∴∠GFC=180°﹣90°﹣30°﹣α=60°﹣α. .......................................12分
25.解:(1)1280;6;16 .......................................3分
(2)小华的速度为:1280÷(20﹣4)=80(米/分),
小明从广场跑去学校的速度为:(1280﹣560)÷(20﹣14)=120(米/分);
.......................................5分
(3)560÷80=7(分),40+4+7=51(分),
答:小华在广场看到小明时是7:51;
.......................................8分
(4)1280÷(560÷8)=(分),
20﹣=(分),
,
答:在保证不迟到的情况下,小明最多可以讲解1次.
.......................................12分
第1页(共1页)
同课章节目录
