2012年高一数学新课程教学课件:4.2《实际问题的函数建模》(北师大版必修1)
文档属性
| 名称 | 2012年高一数学新课程教学课件:4.2《实际问题的函数建模》(北师大版必修1) |  | |
| 格式 | zip | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-05-15 13:53:42 | ||
图片预览










文档简介
(共34张PPT)
§2 实际问题的函数建模
1.了解数学建模,掌握根据已知条件建立函数关系式的
方法;
2.通过例题的学习,增强应用数学的意识以及分析问题、解决问题的能力。
学习目标
④还原:将用数学知识和方法得出的结论,还原为实际问题的意义.
解决应用题的一般程序是:
①审题:弄清题意,分清条件和结论,理顺数量关系;
②建模:将文字语言转化为数学语言,利用数学知识,
建立相应的数学模型;
③解模:求解数学模型,得出数学结论;
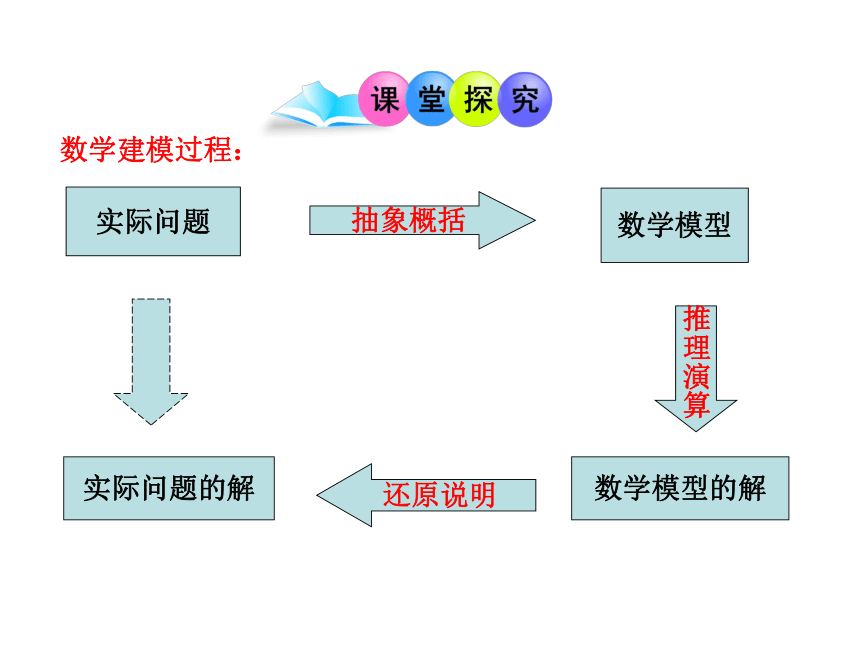
数学建模过程:
实际问题
抽象概括
数学模型
推理演算
数学模型的解
还原说明
实际问题的解
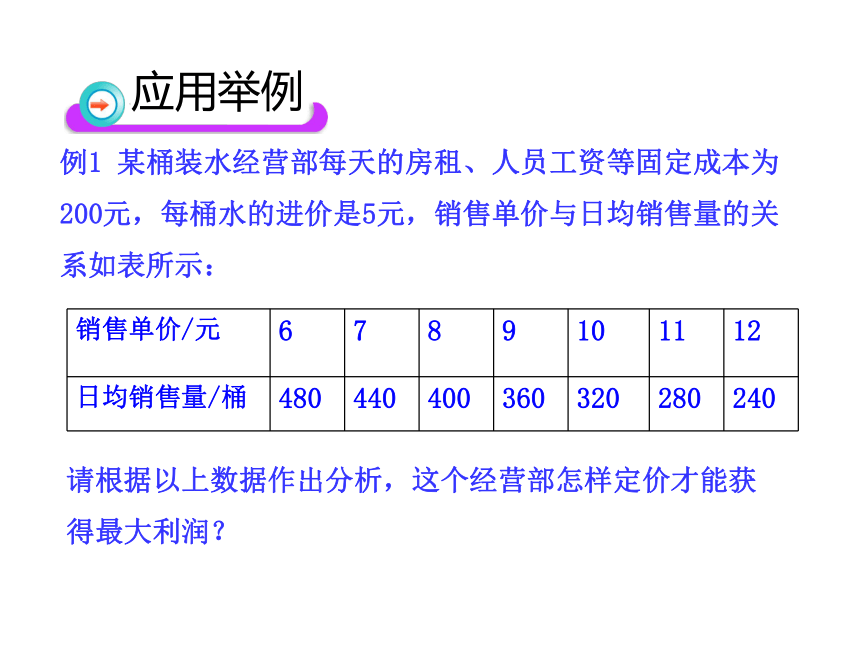
例1 某桶装水经营部每天的房租、人员工资等固定成本为200元,每桶水的进价是5元,销售单价与日均销售量的关系如表所示:
请根据以上数据作出分析,这个经营部怎样定价才能获得最大利润?
销售单价/元 6 7 8 9 10 11 12
日均销售量/桶 480 440 400 360 320 280 240
应用举例
分析:由表中信息可知①销售单价每增加1元,
日均销售量就减少40桶②销售利润怎样计算较好?
解:设在进价基础上增加x元后,日均经营利润为y元,
则有日均销售量为
而
有最大值
只需将销售单价定为11.5元,就可获得最大的利润.
例2 已知某商品的价格每上涨x%,销售的数量就减少kx%,其中k为正常数.
(1)当 时,该商品的价格上涨多少,就能使销售的
总金额最大?
(2)如果适当的涨价,能使销售总金额增加,求k的取值范
围.
解:(1)设商品现在定价为a元,卖出的数量为b个。由题设:
当价格上涨x%时,销售总额为
即
取 ,得:
当 x = 50时, 即该商品的价格上涨50%时,
销售总金额最大.
(2)∵二次函数
在 上递增,
在 上递减
∴适当地涨价,即 x>0 , 即
就是 0 < k <1 ,能使销售总金额增加.
例3、按复利计算利息的一种储蓄,本金为a元,每期利率为r,设本利和为y,存期为x,写出本利和y随存期x变化的函数式。如果存入本金1000元,每期利率2.25%,试计算5期后的本利和是多少?
(1)复利是计算利率的一个方法,即把前一期的利息和本金加在一起做本金,再计算下一期的利息,设本金为P,每期利率为r,本利和为y ,存期为x, 则复利函数式为y=p(1+r)x.
思路分析
(2)1期后本利和为:
2期后本利和为:
……
x期后,本利和为:
将a=1000元,r=2.25%,x=5代入上式:
由计算器算得:y = 1117.68(元)
其中t表示经过的时间, 表示t=0时的人口数,
r表示人口的年平均增长率。
例4. 人口问题是当今世界各国普遍关注的问题,认识人口数量的变化规律,可以为有效控制人口增长提供依据。早在1798年,英国经济学家马尔萨(T.R.Malthus,
1766-1834)就提出了自然状态下的人口增长模型:
年份
1950
1951
1952
1953
1954
1955
1956
1957
1958
1959
人数/万人
55196
56300
57482
58796
60266
61456
62828
64563
65994
67207
下表是1950~1959年我国的人口数据资料:
(1)如果以各年人口增长谐振平均值作为我国这一时期的人口增长率(精确到0.0001),用马尔萨斯人口增长模型建立我国在这一时期具体人口增长模型,并检验所得模型与实际人口数据是否相符;
(2)如果按表的增长趋势,大约在哪一年我国的人口达到13亿
解:(1)设1951~1959年的人口增长率分别为
于是, 1951~1959年期间,我国人口的年均增长率为
由
可得1951的人口增长率为
同理可得,
根据表格中的数据作出散点图,并作出函数的图象.
令
则我国在1950-1959年期间的人口
增长模型为
由图像可以看出,所得模型
与1950~1959年的实际人口数据基本吻合.
所以,如果按上表的增长趋势,那么大约在1950年后的第39年(即1989年)我国的人口就已达到13亿.由此可以看到,如果不实行计划生育,而是让人口自然增长,今天我国将面临难以承受的人口压力.
将y=130000代入
计算可得
(2)海拔为h米处的大气压强为0.5066(105Pa),
求该处的海拔h
(c,k为常量)
y=cekx
在海拔5 (km)处的大气压强为0.5683 (105Pa) ,
在海拔5.5 (km)处的大气压强为0.5366 (105Pa),
(1)问海拔6.710 (km)处的大气压强约为多少?
(精确到0.0001)
y与x之间的函数关系式是
是y(105Pa),
练习:科学研究表明:在海拔x(km)处的大气压强
解:(1)把x=5,y=0.5683,x=5.5,y=0.5366
代入函数表达式y=cekx ,得:
把 x=6.712代入上述函数式,得
≈0.4668 (105Pa)
答:7 (km)高空的大气压强为0.4516 (105Pa).
(2)由1.01·e-0.115x=0.5066
答:该处的海拔为6(km)
解得x=6(km)
例5 以下是某地不同身高的未成年男性的体重平均值表
身高
体重
60
70
80
90
100
110
120
130
140
150
160
170
6.13
7.90
9.99
12.15
15.02
17.50
26.86
20.92
31.11
38.85
47.25
55.05
⑴根据上表中各组对应的数据,能否从我们学过的函数
中找到一种函数,使它比较近似地反映该地未成年男性体重y关于身高x的函数关系,试写出这个函数的解析式,并求出a,b的值.
⑵若体重超过相同身高男性平均值的1.2倍为偏胖,低于0.8倍为偏瘦,那么该地某校一男生身高 175 cm 体重78 kg,他的体重是否正常?
分析:(1)根据上表的数据描点画出图像(如下)
(2)根据上表的数据描点画出图象,观察这个图象,发现各点的连线是一条向上弯曲的曲线,因此,可以判断它不能用函数来近似反映.根据这些点的走向趋势,我们可以考虑用函数来近似反映
解:⑴将已知数据输入计算机,画出图像;
如果取其中的两组数据(70,7.90)(160,47.25)
根据图像,选择函数
进行拟合.
代入函数
由计算器得
从而函数模型为
将已知数据代人所得函数关系式,或作出所得函数的图象,可知函数能较好地反映该地区未成年男性体重与身高的关系.
所以,该地区未成年男性体重关于身高的函数关系式可以选为
⑵将x=175代人
得
有计算器计算得 y=63.98,
所以,这个男生体重偏胖.
由于
点评:函数拟合与预测的步骤:
⑴ 能够根据原始数据、表格. 绘出散点图;
⑵ 通过考察散点图,画出“最贴近”的直线或曲线,即拟合直线或拟合曲线.
如果所有实际点都落到了拟合直线或曲线上,一“点”不漏,那么这将是个十分完美的事情,但在实际应用中,这种情况是不可能发生的.
⑷利用函数关系式,根据条件对所给问题进行预测和控制,为决策和管理提供依据.
因此,使实际点尽可能均匀分布在直线或曲线两侧,使两侧的点大体相等,得出的拟合直线或拟合曲线就是“最贴近”的了.
⑶根据所学函数知识,求出拟合直线或拟合曲线的函数关系式.
1.一家旅社有100间相同的客房,经过一段时间的经营实践,
旅社经理发现,每间客房每天的价格与住房率之间有如下关系:
每间每天房价
住房率
20元
18元
16元
14元
65%
75%
85%
95%
要使每天收入达到最高,每间定价应为( )
A.20元 B.18元 C.16元 D.14元
C
2.将进货单价为80元的商品按90元一个售出时,能卖出400
个,已知这种商品每个涨价1元,其销售量就减少20个,为
了取得最大利润,每个售价应定为( )
A.95元 B.100元 C.105元 D.110元
A
y=(90+x-80)(400-20x)
为常数),
已知四月份该产品的产量为1.37万件,
请问:用以上那个函数作模拟函数较好?说明理由。
3.某工厂今年1月、2月、3月生产某产品分别为1万件、1.2万件、1.3万件,为估计以后每月的产量,以这三个月的产量为依据,用一个函数模拟该产品的月产量y与月份x的关系,模拟函数可选用二次函数或
解:设二次函数为:
由已知得
所以
当x=4时,
又对于函数
由已知得:
所以
当x=4时,
由四月份的实际产量为1.37万件,
∴选用函数 作模拟函数较好。
(2)利用待定系数法,确定具体函数模型;
1.利用给定函数模型或建立确定的函数模型解决实际问题的方法;
(3)对所确定的函数模型进行适当的评价;
(1)根据题意选用恰当的函数模型来描述所涉及的数量之间的关系;
(4)根据实际问题对模型进行适当的修正.
2.本节课的体会:根据收集到的数据,作出散点图,然后通过观察图象,判断问题适用的函数模型,借助计算器或计算机数据处理功能,利用待定系数法得出具体的函数解析式,再利用得到的函数模型解决相应的问题,这是函数应用的一个基本过程.
§2 实际问题的函数建模
1.了解数学建模,掌握根据已知条件建立函数关系式的
方法;
2.通过例题的学习,增强应用数学的意识以及分析问题、解决问题的能力。
学习目标
④还原:将用数学知识和方法得出的结论,还原为实际问题的意义.
解决应用题的一般程序是:
①审题:弄清题意,分清条件和结论,理顺数量关系;
②建模:将文字语言转化为数学语言,利用数学知识,
建立相应的数学模型;
③解模:求解数学模型,得出数学结论;
数学建模过程:
实际问题
抽象概括
数学模型
推理演算
数学模型的解
还原说明
实际问题的解
例1 某桶装水经营部每天的房租、人员工资等固定成本为200元,每桶水的进价是5元,销售单价与日均销售量的关系如表所示:
请根据以上数据作出分析,这个经营部怎样定价才能获得最大利润?
销售单价/元 6 7 8 9 10 11 12
日均销售量/桶 480 440 400 360 320 280 240
应用举例
分析:由表中信息可知①销售单价每增加1元,
日均销售量就减少40桶②销售利润怎样计算较好?
解:设在进价基础上增加x元后,日均经营利润为y元,
则有日均销售量为
而
有最大值
只需将销售单价定为11.5元,就可获得最大的利润.
例2 已知某商品的价格每上涨x%,销售的数量就减少kx%,其中k为正常数.
(1)当 时,该商品的价格上涨多少,就能使销售的
总金额最大?
(2)如果适当的涨价,能使销售总金额增加,求k的取值范
围.
解:(1)设商品现在定价为a元,卖出的数量为b个。由题设:
当价格上涨x%时,销售总额为
即
取 ,得:
当 x = 50时, 即该商品的价格上涨50%时,
销售总金额最大.
(2)∵二次函数
在 上递增,
在 上递减
∴适当地涨价,即 x>0 , 即
就是 0 < k <1 ,能使销售总金额增加.
例3、按复利计算利息的一种储蓄,本金为a元,每期利率为r,设本利和为y,存期为x,写出本利和y随存期x变化的函数式。如果存入本金1000元,每期利率2.25%,试计算5期后的本利和是多少?
(1)复利是计算利率的一个方法,即把前一期的利息和本金加在一起做本金,再计算下一期的利息,设本金为P,每期利率为r,本利和为y ,存期为x, 则复利函数式为y=p(1+r)x.
思路分析
(2)1期后本利和为:
2期后本利和为:
……
x期后,本利和为:
将a=1000元,r=2.25%,x=5代入上式:
由计算器算得:y = 1117.68(元)
其中t表示经过的时间, 表示t=0时的人口数,
r表示人口的年平均增长率。
例4. 人口问题是当今世界各国普遍关注的问题,认识人口数量的变化规律,可以为有效控制人口增长提供依据。早在1798年,英国经济学家马尔萨(T.R.Malthus,
1766-1834)就提出了自然状态下的人口增长模型:
年份
1950
1951
1952
1953
1954
1955
1956
1957
1958
1959
人数/万人
55196
56300
57482
58796
60266
61456
62828
64563
65994
67207
下表是1950~1959年我国的人口数据资料:
(1)如果以各年人口增长谐振平均值作为我国这一时期的人口增长率(精确到0.0001),用马尔萨斯人口增长模型建立我国在这一时期具体人口增长模型,并检验所得模型与实际人口数据是否相符;
(2)如果按表的增长趋势,大约在哪一年我国的人口达到13亿
解:(1)设1951~1959年的人口增长率分别为
于是, 1951~1959年期间,我国人口的年均增长率为
由
可得1951的人口增长率为
同理可得,
根据表格中的数据作出散点图,并作出函数的图象.
令
则我国在1950-1959年期间的人口
增长模型为
由图像可以看出,所得模型
与1950~1959年的实际人口数据基本吻合.
所以,如果按上表的增长趋势,那么大约在1950年后的第39年(即1989年)我国的人口就已达到13亿.由此可以看到,如果不实行计划生育,而是让人口自然增长,今天我国将面临难以承受的人口压力.
将y=130000代入
计算可得
(2)海拔为h米处的大气压强为0.5066(105Pa),
求该处的海拔h
(c,k为常量)
y=cekx
在海拔5 (km)处的大气压强为0.5683 (105Pa) ,
在海拔5.5 (km)处的大气压强为0.5366 (105Pa),
(1)问海拔6.710 (km)处的大气压强约为多少?
(精确到0.0001)
y与x之间的函数关系式是
是y(105Pa),
练习:科学研究表明:在海拔x(km)处的大气压强
解:(1)把x=5,y=0.5683,x=5.5,y=0.5366
代入函数表达式y=cekx ,得:
把 x=6.712代入上述函数式,得
≈0.4668 (105Pa)
答:7 (km)高空的大气压强为0.4516 (105Pa).
(2)由1.01·e-0.115x=0.5066
答:该处的海拔为6(km)
解得x=6(km)
例5 以下是某地不同身高的未成年男性的体重平均值表
身高
体重
60
70
80
90
100
110
120
130
140
150
160
170
6.13
7.90
9.99
12.15
15.02
17.50
26.86
20.92
31.11
38.85
47.25
55.05
⑴根据上表中各组对应的数据,能否从我们学过的函数
中找到一种函数,使它比较近似地反映该地未成年男性体重y关于身高x的函数关系,试写出这个函数的解析式,并求出a,b的值.
⑵若体重超过相同身高男性平均值的1.2倍为偏胖,低于0.8倍为偏瘦,那么该地某校一男生身高 175 cm 体重78 kg,他的体重是否正常?
分析:(1)根据上表的数据描点画出图像(如下)
(2)根据上表的数据描点画出图象,观察这个图象,发现各点的连线是一条向上弯曲的曲线,因此,可以判断它不能用函数来近似反映.根据这些点的走向趋势,我们可以考虑用函数来近似反映
解:⑴将已知数据输入计算机,画出图像;
如果取其中的两组数据(70,7.90)(160,47.25)
根据图像,选择函数
进行拟合.
代入函数
由计算器得
从而函数模型为
将已知数据代人所得函数关系式,或作出所得函数的图象,可知函数能较好地反映该地区未成年男性体重与身高的关系.
所以,该地区未成年男性体重关于身高的函数关系式可以选为
⑵将x=175代人
得
有计算器计算得 y=63.98,
所以,这个男生体重偏胖.
由于
点评:函数拟合与预测的步骤:
⑴ 能够根据原始数据、表格. 绘出散点图;
⑵ 通过考察散点图,画出“最贴近”的直线或曲线,即拟合直线或拟合曲线.
如果所有实际点都落到了拟合直线或曲线上,一“点”不漏,那么这将是个十分完美的事情,但在实际应用中,这种情况是不可能发生的.
⑷利用函数关系式,根据条件对所给问题进行预测和控制,为决策和管理提供依据.
因此,使实际点尽可能均匀分布在直线或曲线两侧,使两侧的点大体相等,得出的拟合直线或拟合曲线就是“最贴近”的了.
⑶根据所学函数知识,求出拟合直线或拟合曲线的函数关系式.
1.一家旅社有100间相同的客房,经过一段时间的经营实践,
旅社经理发现,每间客房每天的价格与住房率之间有如下关系:
每间每天房价
住房率
20元
18元
16元
14元
65%
75%
85%
95%
要使每天收入达到最高,每间定价应为( )
A.20元 B.18元 C.16元 D.14元
C
2.将进货单价为80元的商品按90元一个售出时,能卖出400
个,已知这种商品每个涨价1元,其销售量就减少20个,为
了取得最大利润,每个售价应定为( )
A.95元 B.100元 C.105元 D.110元
A
y=(90+x-80)(400-20x)
为常数),
已知四月份该产品的产量为1.37万件,
请问:用以上那个函数作模拟函数较好?说明理由。
3.某工厂今年1月、2月、3月生产某产品分别为1万件、1.2万件、1.3万件,为估计以后每月的产量,以这三个月的产量为依据,用一个函数模拟该产品的月产量y与月份x的关系,模拟函数可选用二次函数或
解:设二次函数为:
由已知得
所以
当x=4时,
又对于函数
由已知得:
所以
当x=4时,
由四月份的实际产量为1.37万件,
∴选用函数 作模拟函数较好。
(2)利用待定系数法,确定具体函数模型;
1.利用给定函数模型或建立确定的函数模型解决实际问题的方法;
(3)对所确定的函数模型进行适当的评价;
(1)根据题意选用恰当的函数模型来描述所涉及的数量之间的关系;
(4)根据实际问题对模型进行适当的修正.
2.本节课的体会:根据收集到的数据,作出散点图,然后通过观察图象,判断问题适用的函数模型,借助计算器或计算机数据处理功能,利用待定系数法得出具体的函数解析式,再利用得到的函数模型解决相应的问题,这是函数应用的一个基本过程.
