2012年高一数学新课程教学课件:4.1.1《利用函数性质判定方程解的存在》(北师大版必修1)
文档属性
| 名称 | 2012年高一数学新课程教学课件:4.1.1《利用函数性质判定方程解的存在》(北师大版必修1) |
|
|
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-05-15 00:00:00 | ||
图片预览




文档简介
(共17张PPT)
第四章 函数应用
§1 函数与方程
1.1 利用函数性质判定
方程解的存在
1.理解函数(结合二次函数)零点的概念,领会函数零点
与相应方程解的关系.
2.掌握零点存在的判定条件.
学习目标
韦达(Viete,Francois,seigneurdeLaBigotiere)是法国
十六世纪最有影响的数学家之一。
第一个引进系统的代数符号,并对方程论做了改进。
他的《解析方法入门》一书(1591年),集中了他以前在代数方面的大成,使代数学真正成为数学中的一个优秀分支。他对方程论的贡献是在《论方程的整理和修正》一书中提出了二次、三次和四次方程的解。
引入新课
第一个有意识地和系统地使用字母来表示已知数、未知数及其乘幂,带来了代数学理论研究的重大进步。韦达讨论了方程根的各种有理变换,发现了方程根与系数之间的关系(所以人们把叙述一元二次方程根与系数关系的结论称为“韦达定理”)。
x
y
o
1
-1
2
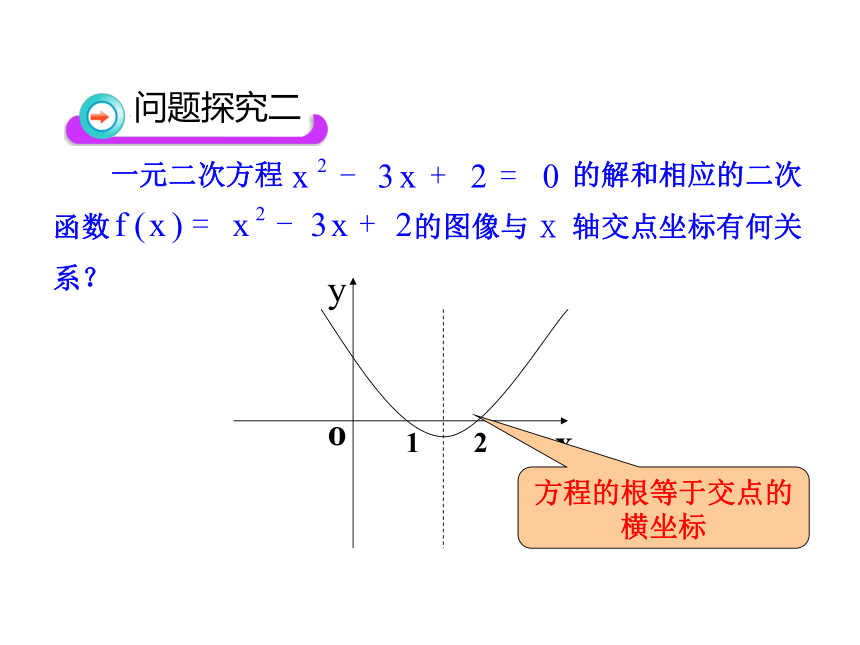
一元一次方程 的解和相应的一次函数
的图像与 轴交点坐标有何关系?
x
方程的根等于交点的横坐标
问题探究一
x
y
o
1
2
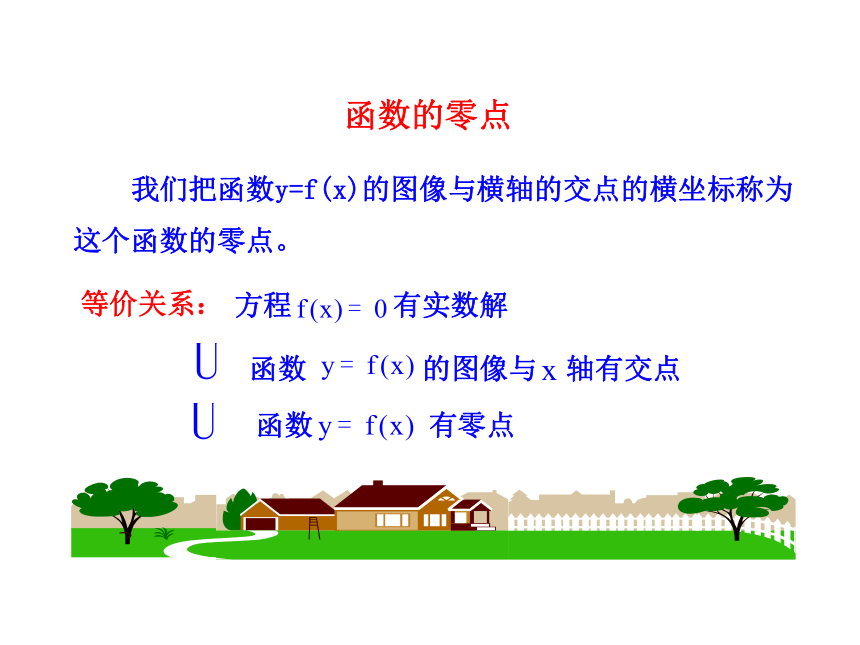
一元二次方程 的解和相应的二次函数 的图像与 轴交点坐标有何关系?
x
方程的根等于交点的横坐标
问题探究二
函数的零点
我们把函数y=f(x)的图像与横轴的交点的横坐标称为这个函数的零点。
方程 有实数解
函数 的图像与 轴有交点
函数 有零点
等价关系:
1.利用函数图像判断下列方程有没有实数解,有几个:
(1)-x2+3x+5=0;
(2)2x(x-2)=-3;
有,2个
x
y
0
没有
巩固练习1
(3) x2 =4x-4;
(4)5 x2 +2x=3 x2 +5.
有,2个
有,1个
观察二次函数f(x)=x2-2x-3的图像:
[-2,1] f(-2)>0 f(1)<0
f(-2)·f(1)<0 (-2,1)x=-1
x2-2x-3=0的一个解
[2,4] f(2)<0 f(4)>0 f(2)·f(4)<0
(2,4)x=3 x2-2x-3=0的另一个解
.
.
.
.
.
x
y
0
-1
3
2
1
1
2
-1
-2
-3
-4
-2
4
知识探究
零点存在定理:
若函数y=f(x)在区间[a,b]上的图像是连续曲线,
并且在区间端点的函数值符号相反,即f(a)·f(b)<0,则在区间(a,b)内,函数y=f(x)至少有一个零点,即相应的方程f(x)=0在区间(a,b) 内至少有一个实数解.
注:只要满足上述两个条件,就能判断函数在指定区间内存在零点。
x
y
0
a
b
.
.
x
y
0
a
b
x
y
0
a
b
.
.
.
.
1.如果二次函数y=x2+2x+(m+3)有两个不同的零点,则m的
取值范围是( )
A. m>–2 B.m<–2 C.m>2 D.m<2
2.函数f(x)= – x3 – 3x+5的零点所在的大致区间为
( )
A.(1,2) B.(–2,0)
C.(0,1) D.(0,0.5 )
B
A
巩固练习2
应用举例
1.在二次函数 中,ac<0,则其零点的个数为( )
A.1 B.2 C.3 D.不存在
B
2.已知函数f(x)的图像是连续不断的,有如下的x,f(x)
对应值表:
x 1 2 3 4 5 6 7
f(x) 23 9 –7 11 –5 –12 –26
那么函数在区间[1,6]上的零点至少有( )个
A.5 B.4 C.3 D.2
C
1.函数零点的定义
2.等价关系
3.函数的零点或相应方程的
根的存在性以及个数的判断
第四章 函数应用
§1 函数与方程
1.1 利用函数性质判定
方程解的存在
1.理解函数(结合二次函数)零点的概念,领会函数零点
与相应方程解的关系.
2.掌握零点存在的判定条件.
学习目标
韦达(Viete,Francois,seigneurdeLaBigotiere)是法国
十六世纪最有影响的数学家之一。
第一个引进系统的代数符号,并对方程论做了改进。
他的《解析方法入门》一书(1591年),集中了他以前在代数方面的大成,使代数学真正成为数学中的一个优秀分支。他对方程论的贡献是在《论方程的整理和修正》一书中提出了二次、三次和四次方程的解。
引入新课
第一个有意识地和系统地使用字母来表示已知数、未知数及其乘幂,带来了代数学理论研究的重大进步。韦达讨论了方程根的各种有理变换,发现了方程根与系数之间的关系(所以人们把叙述一元二次方程根与系数关系的结论称为“韦达定理”)。
x
y
o
1
-1
2
一元一次方程 的解和相应的一次函数
的图像与 轴交点坐标有何关系?
x
方程的根等于交点的横坐标
问题探究一
x
y
o
1
2
一元二次方程 的解和相应的二次函数 的图像与 轴交点坐标有何关系?
x
方程的根等于交点的横坐标
问题探究二
函数的零点
我们把函数y=f(x)的图像与横轴的交点的横坐标称为这个函数的零点。
方程 有实数解
函数 的图像与 轴有交点
函数 有零点
等价关系:
1.利用函数图像判断下列方程有没有实数解,有几个:
(1)-x2+3x+5=0;
(2)2x(x-2)=-3;
有,2个
x
y
0
没有
巩固练习1
(3) x2 =4x-4;
(4)5 x2 +2x=3 x2 +5.
有,2个
有,1个
观察二次函数f(x)=x2-2x-3的图像:
[-2,1] f(-2)>0 f(1)<0
f(-2)·f(1)<0 (-2,1)x=-1
x2-2x-3=0的一个解
[2,4] f(2)<0 f(4)>0 f(2)·f(4)<0
(2,4)x=3 x2-2x-3=0的另一个解
.
.
.
.
.
x
y
0
-1
3
2
1
1
2
-1
-2
-3
-4
-2
4
知识探究
零点存在定理:
若函数y=f(x)在区间[a,b]上的图像是连续曲线,
并且在区间端点的函数值符号相反,即f(a)·f(b)<0,则在区间(a,b)内,函数y=f(x)至少有一个零点,即相应的方程f(x)=0在区间(a,b) 内至少有一个实数解.
注:只要满足上述两个条件,就能判断函数在指定区间内存在零点。
x
y
0
a
b
.
.
x
y
0
a
b
x
y
0
a
b
.
.
.
.
1.如果二次函数y=x2+2x+(m+3)有两个不同的零点,则m的
取值范围是( )
A. m>–2 B.m<–2 C.m>2 D.m<2
2.函数f(x)= – x3 – 3x+5的零点所在的大致区间为
( )
A.(1,2) B.(–2,0)
C.(0,1) D.(0,0.5 )
B
A
巩固练习2
应用举例
1.在二次函数 中,ac<0,则其零点的个数为( )
A.1 B.2 C.3 D.不存在
B
2.已知函数f(x)的图像是连续不断的,有如下的x,f(x)
对应值表:
x 1 2 3 4 5 6 7
f(x) 23 9 –7 11 –5 –12 –26
那么函数在区间[1,6]上的零点至少有( )个
A.5 B.4 C.3 D.2
C
1.函数零点的定义
2.等价关系
3.函数的零点或相应方程的
根的存在性以及个数的判断
