11.2.2三角形的外角同步随堂练习题 2021-2022学年八年级数学人教版上册(word版含解析)
文档属性
| 名称 | 11.2.2三角形的外角同步随堂练习题 2021-2022学年八年级数学人教版上册(word版含解析) |
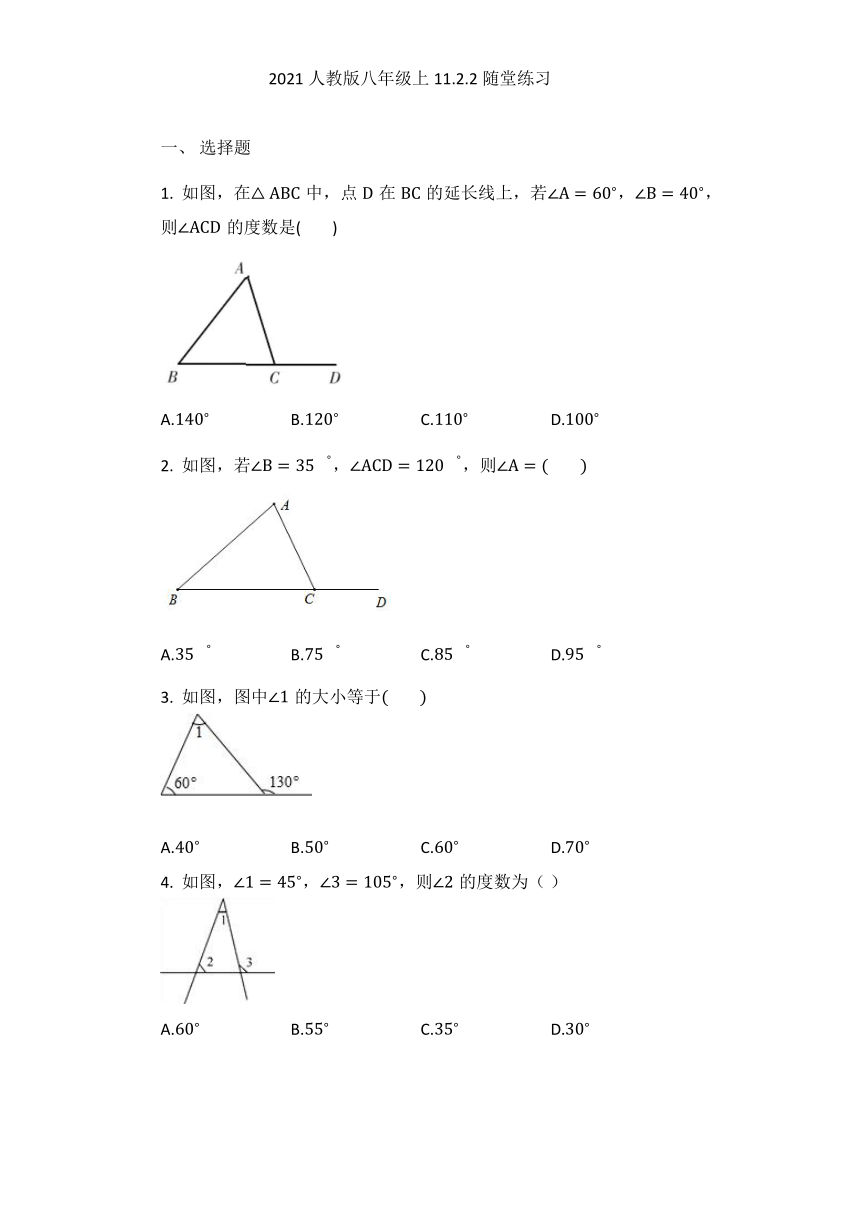
|
|
| 格式 | docx | ||
| 文件大小 | 118.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-15 21:28:23 | ||
图片预览
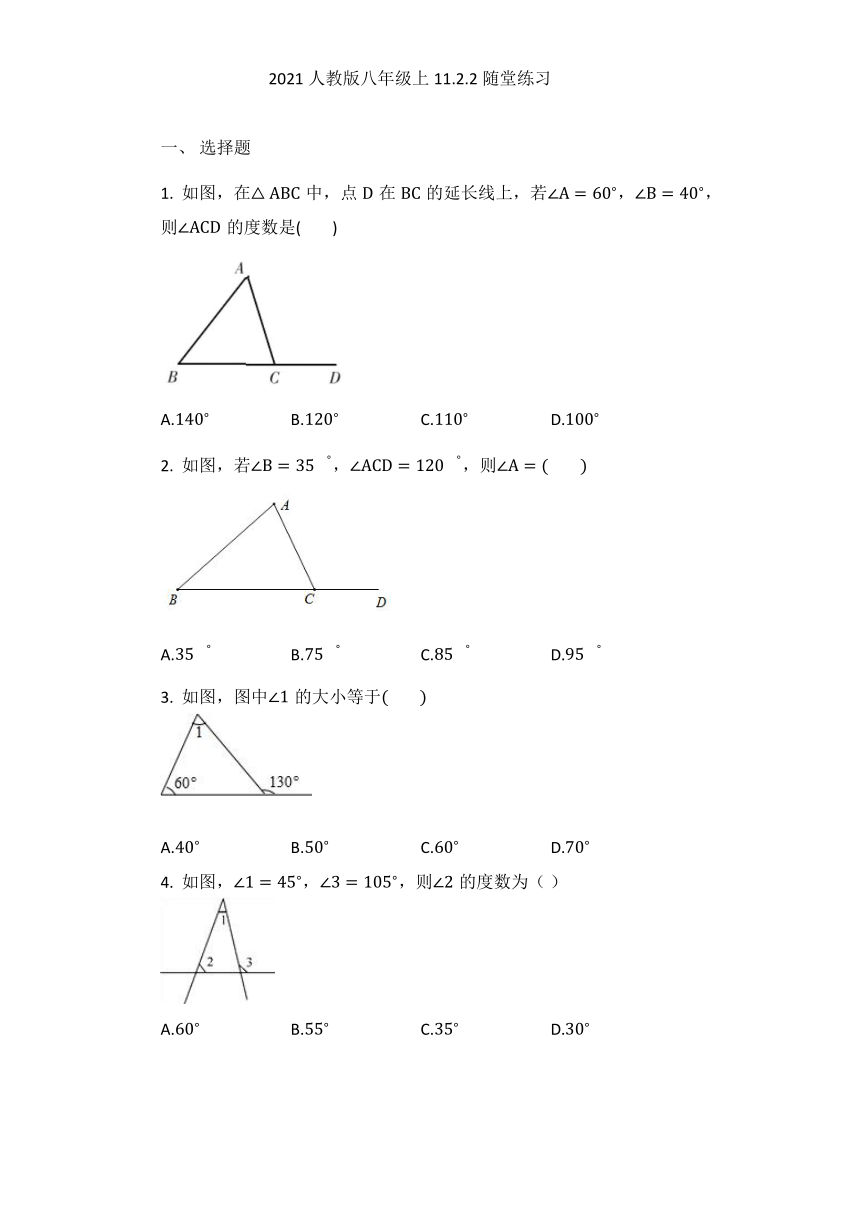




文档简介
2021人教版八年级上11.2.2随堂练习
一、
选择题
1.
如图,在中,点在的延长线上,若,则的度数是(?
?
?
?
)
A.
B.
C.
D.
2.
如图,若,,则?
?
?
?
A.
B.
C.
D.
3.
如图,图中的大小等于?
?
?
?
?
A.
B.
C.
D.
4.
如图,,,则的度数为(
)
A.
B.
C.
D.
5.
如图,,,的大小关系是(
)
A.
B.
C.
D.
6.
如图,在中,=,沿折叠,使点恰好落在边上点处,若=,则的大小为(
)
A.
B.
C.
D.
7.
如图,在中,=,沿折叠,使点恰好落在边上的点处,若=,则的度数为(
)
A.
B.
C.
D.
8.
已知的外角,的角平分线,交于点,则是(
)
A.钝角
B.锐角
C.直角
D.无法确定
9.
如图所示,一副三角板放在两条平行线,之间,含角的三角板的较长直角边在直线上,含角的三角板的一条直角边在另一个三角板的斜边上,则的度数是(?
?
?
?
)
A.
B.
C.
D.
10.
如图,将纸片沿着折叠,若=,则的大小为(
)
A.
B.
C.
D.
二、
填空题
?
11.
中,=,=,则=________.
12.
在直角三角形中,两个锐角的度数比为,那么较小锐角的度数是________.
13.
如图,在四边形中,与互补,为延长线上的点,且,则的度数是________.
14.
如图,在中,,分别平分和,=,则=________度.
三、
解答题
?
15.
如图,在中,,是的一条高线,若.求的度数.
?
16.
如图,,求证:,.
?
17.
如图所示,直线和相交于点,,,交于点,且,,求证:.
参考答案与试题解析
一、
选择题
1.
【答案】
D
【解答】
解:∵
是的一个外角,
∴
,
∵
,,
∴
.
故选.
2.
【答案】
C
【解答】
解:由题意可得:?.
故选.
3.
【答案】
D
【解答】
解:由三角形的外角性质得,.
故选.
4.
【答案】
A
【解答】
此题暂无解答
5.
【答案】
B
【解答】
解:∵
是的外角,
∴
,
∵
是的外角,
∴
,
∴
,
故选:.
6.
【答案】
A
【解答】
∵
在中,=,=,
∴
==,
根据折叠可得=,
∴
==,
7.
【答案】
B
【解答】
此题暂无解答
8.
【答案】
B
【解答】
解:∵
的外角平分线,交于点,
∴
,,
∵
、是的两个外角,
∴
,
∴
,
∵
在中,,
∴
是锐角.
故选:.
9.
【答案】
D
【解答】
解:延长交于点,则,
∴
.
∵
,
∴
,
∴
.
故选.
10.
【答案】
C
【解答】
根据折叠及邻补角的性质,得
=,=,
∴
=,
∵
=
∴
=,
∴
在中,由内角和定理,得
==,
二、
填空题
11.
【答案】
【解答】
此题暂无解答
12.
【答案】
【解答】
解:设两锐角分别为、,由题意得
解得
所以较小锐角的度数为
故答案为:
13.
【答案】
【解答】
此题暂无解答
14.
【答案】
【解答】
此题暂无解答
三、
解答题
15.
【答案】
解:∵
,
∴
,
∵
是的一条高线,
∴
,
∴
.
【解答】
解:∵
,
∴
,
∵
是的一条高线,
∴
,
∴
.
16.
【答案】
证明:∵
,
∴
,
∵
,
∴
,
∴
;
同理可得.
【解答】
证明:∵
,
∴
,
∵
,
∴
,
∴
;
同理可得.
17.
【答案】
证明:延长交与点,根据三角形的外角性质,得
,,
∴
.
【解答】
证明:延长交与点,根据三角形的外角性质,得
,,
∴
.
一、
选择题
1.
如图,在中,点在的延长线上,若,则的度数是(?
?
?
?
)
A.
B.
C.
D.
2.
如图,若,,则?
?
?
?
A.
B.
C.
D.
3.
如图,图中的大小等于?
?
?
?
?
A.
B.
C.
D.
4.
如图,,,则的度数为(
)
A.
B.
C.
D.
5.
如图,,,的大小关系是(
)
A.
B.
C.
D.
6.
如图,在中,=,沿折叠,使点恰好落在边上点处,若=,则的大小为(
)
A.
B.
C.
D.
7.
如图,在中,=,沿折叠,使点恰好落在边上的点处,若=,则的度数为(
)
A.
B.
C.
D.
8.
已知的外角,的角平分线,交于点,则是(
)
A.钝角
B.锐角
C.直角
D.无法确定
9.
如图所示,一副三角板放在两条平行线,之间,含角的三角板的较长直角边在直线上,含角的三角板的一条直角边在另一个三角板的斜边上,则的度数是(?
?
?
?
)
A.
B.
C.
D.
10.
如图,将纸片沿着折叠,若=,则的大小为(
)
A.
B.
C.
D.
二、
填空题
?
11.
中,=,=,则=________.
12.
在直角三角形中,两个锐角的度数比为,那么较小锐角的度数是________.
13.
如图,在四边形中,与互补,为延长线上的点,且,则的度数是________.
14.
如图,在中,,分别平分和,=,则=________度.
三、
解答题
?
15.
如图,在中,,是的一条高线,若.求的度数.
?
16.
如图,,求证:,.
?
17.
如图所示,直线和相交于点,,,交于点,且,,求证:.
参考答案与试题解析
一、
选择题
1.
【答案】
D
【解答】
解:∵
是的一个外角,
∴
,
∵
,,
∴
.
故选.
2.
【答案】
C
【解答】
解:由题意可得:?.
故选.
3.
【答案】
D
【解答】
解:由三角形的外角性质得,.
故选.
4.
【答案】
A
【解答】
此题暂无解答
5.
【答案】
B
【解答】
解:∵
是的外角,
∴
,
∵
是的外角,
∴
,
∴
,
故选:.
6.
【答案】
A
【解答】
∵
在中,=,=,
∴
==,
根据折叠可得=,
∴
==,
7.
【答案】
B
【解答】
此题暂无解答
8.
【答案】
B
【解答】
解:∵
的外角平分线,交于点,
∴
,,
∵
、是的两个外角,
∴
,
∴
,
∵
在中,,
∴
是锐角.
故选:.
9.
【答案】
D
【解答】
解:延长交于点,则,
∴
.
∵
,
∴
,
∴
.
故选.
10.
【答案】
C
【解答】
根据折叠及邻补角的性质,得
=,=,
∴
=,
∵
=
∴
=,
∴
在中,由内角和定理,得
==,
二、
填空题
11.
【答案】
【解答】
此题暂无解答
12.
【答案】
【解答】
解:设两锐角分别为、,由题意得
解得
所以较小锐角的度数为
故答案为:
13.
【答案】
【解答】
此题暂无解答
14.
【答案】
【解答】
此题暂无解答
三、
解答题
15.
【答案】
解:∵
,
∴
,
∵
是的一条高线,
∴
,
∴
.
【解答】
解:∵
,
∴
,
∵
是的一条高线,
∴
,
∴
.
16.
【答案】
证明:∵
,
∴
,
∵
,
∴
,
∴
;
同理可得.
【解答】
证明:∵
,
∴
,
∵
,
∴
,
∴
;
同理可得.
17.
【答案】
证明:延长交与点,根据三角形的外角性质,得
,,
∴
.
【解答】
证明:延长交与点,根据三角形的外角性质,得
,,
∴
.
