11.3.2多边形的内角和同步练习2021-2022学年人教版八年级上册(word版含解析)
文档属性
| 名称 | 11.3.2多边形的内角和同步练习2021-2022学年人教版八年级上册(word版含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 138.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-15 00:00:00 | ||
图片预览




文档简介
2021人教版八年级上11.3.2同步练习
一、
选择题
1.
若一个多边形的每一个内角都等于,则它是?
?
?
?
A.四边形
B.五边形
C.六边形
D.八边形
2.
若一个多边形内角和等于,则该多边形边数是???
A.
B.
C.
D.
3.
若一个正多边形的每个内角都为,则这个正多边形的边数是(
)
A.
B.
C.
D.
4.
在多边形内角和公式的探究过程中,主要运用的数学思想是(?
?
?
?
)
A.分类讨论思想
B.化归思想
C.方程思想
D.整体思想
5.
一个多边形的内角和比外角和的三倍少,则这个多边形是(?
?
?
?
)
A.四边形
B.五边形
C.六边形
D.七边形
6.
已知一个多边形的内角和是外角和的倍,则这个多边形是(
)
A.五边形
B.六边形
C.七边形
D.八边形
7.
如果一个多边形的内角和是它的外角和的倍,那么从这个多边形的一个顶点出发的对角线的条数是(
)
A.
B.
C.
D.
8.
将一矩形纸片沿一条直线剪成两个多边形,那么这两个多边形的内角和之和不可能是?
?
?
?
A.
B.
C.
D.
9.
把一个正方形锯掉一个角,剩下的多边形是(
)
A.三角形
B.四边形
C.五边形
D.三角形或四边形或五边形
10.
已知凸边形有条对角线,则此多边形的内角和是?
?
?
?
A.?
B.
C.
D.
11.
从边形的一个顶点出发一共可引条对角线,则这个边形的内角和等于(
)
A.
B.
C.
D.
二、
填空题
12.
六边形的内角和等于________.
13.
一个多边形的每个外角都是,则这个多边形是________边形,它的对角线共有________条.
?14.
正边形每一个外角都是度,则________,它共有________条对角线.
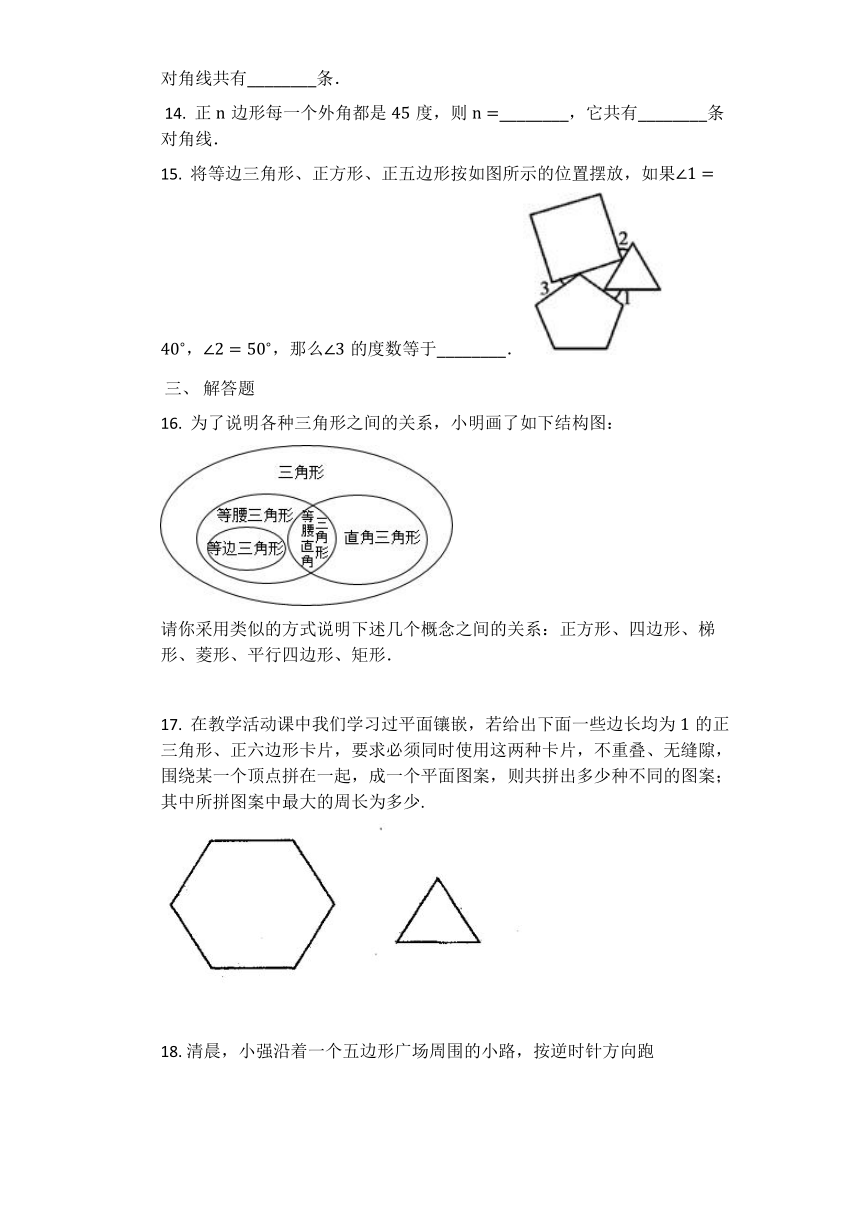
15.
将等边三角形、正方形、正五边形按如图所示的位置摆放,如果,,那么的度数等于________.
三、
解答题
?
16.
为了说明各种三角形之间的关系,小明画了如下结构图:
请你采用类似的方式说明下述几个概念之间的关系:正方形、四边形、梯形、菱形、平行四边形、矩形.
?
17.
在教学活动课中我们学面镶嵌,若给出下面一些边长均为的正三角形、正六边形卡片,要求必须同时使用这两种卡片,不重叠、无缝隙,围绕某一个顶点拼在一起,成一个平面图案,则共拼出多少种不同的图案;其中所拼图案中最大的周长为多少.
?
18.
清晨,小强沿着一个五边形广场周围的小路,按逆时针方向跑步.
(1)小强每从一条街道转到下一条街道时,身体转过的角是哪些角在图上标出它们.
(2)他每跑完一圈,身体转过的角度之和是多少?
(3)在图中,你能求出吗?你是怎样得到的?
(4)如果广场是六边形、八边形的形状,那么还有类似的结论吗?
参考答案与试题解析
一、
选择题
1.
【答案】
C
【解答】
解:∵
多边形的每一个内角都等于,
∴
多边形的每一个外角都等于,
∴
边数.
故选.
2.
【答案】
B
【解答】
此题暂无解答
3.
【答案】
B
【解答】
∵
一个正多边形的每个内角都为,
∴
此多边形的每一个外角是:=,
∴
这个正多边形的边数是:=,
4.
【答案】
B
【解答】
解:多边形内角和定理:且为整数),该公式推导的基本方法是从边形的一个顶点出发引出条对角线,将边形分割为个三角形,这个三角形的所有内角之和正好是边形的内角和,体现了化归思想.
故选.
5.
【答案】
D
【解答】
解:设这个多边形的边数为,
由于多边形中边形的内角和等于,且任意多边形的外角和都为
根据题意可知,
解得
即这个多边形的边数是,
故选.
6.
【答案】
D
【解答】
设多边形的边数是,则
解得:
故选.
7.
【答案】
A
【解答】
解:设这个多边形有条边,由题意得:
,
解得;,
从这个多边形的一个顶点出发的对角线的条数是,
故选:.
8.
【答案】
D
【解答】
解:①将矩形沿对角线剪开,得到两个三角形,
两个多边形的内角和为:=;
②将矩形从一顶点剪向对边,
得到一个三角形和一个四边形,
两个多边形的内角和为:=;
③将矩形沿一组对边剪开,得到两个四边形,
两个多边形的内角和为:=;
④将矩形沿一组邻边剪开,
得到一个三角形和一个五边形,
其内角和为:=.
故选.
9.
【答案】
D
【解答】
解:如图所示:
,
故选:.
10.
【答案】
B
【解答】
解:∵
凸边形有条对角线,
∴
,
解得:(舍去),或,
即多边形的边数是,
∴
这个多边形的内角和.
故选.
11.
【答案】
A
【解答】
解:∵
从边形的一个顶点出发一共可引条对角线,
∴
多边形是边形,
∴
内角和是,
故选.
二、
填空题
12.
【答案】
【解答】
解:边形的内角和是,
则六边形的内角和等于.
故答案为:.
13.
【答案】
六,
【解答】
解:,
,
故答案为:六;.
14.
【答案】
,
【解答】
解:,所以这个正多边形是正八边形.
对角线条数:.
故答案为:;.
15.
【答案】
【解答】
此题暂无解答
三、
解答题
16.
【答案】
解:如图所示:
【解答】
解:如图所示:
17.
【答案】
解:共拼出中不同的图案,如图所示:
由图象可知最大周长为.
【解答】
解:共拼出中不同的图案,如图所示:
由图象可知最大周长为.
18.
【答案】
解:,,,,;
(2)∵
各角是五边形的外角,
∴
身体转过的角度之和是;
(3),
因为各角是五边形的外角;
(4)多边形外角和为度.
【解答】
解:,,,,;
(2)∵
各角是五边形的外角,
∴
身体转过的角度之和是;
(3),
因为各角是五边形的外角;
(4)多边形外角和为度.
一、
选择题
1.
若一个多边形的每一个内角都等于,则它是?
?
?
?
A.四边形
B.五边形
C.六边形
D.八边形
2.
若一个多边形内角和等于,则该多边形边数是???
A.
B.
C.
D.
3.
若一个正多边形的每个内角都为,则这个正多边形的边数是(
)
A.
B.
C.
D.
4.
在多边形内角和公式的探究过程中,主要运用的数学思想是(?
?
?
?
)
A.分类讨论思想
B.化归思想
C.方程思想
D.整体思想
5.
一个多边形的内角和比外角和的三倍少,则这个多边形是(?
?
?
?
)
A.四边形
B.五边形
C.六边形
D.七边形
6.
已知一个多边形的内角和是外角和的倍,则这个多边形是(
)
A.五边形
B.六边形
C.七边形
D.八边形
7.
如果一个多边形的内角和是它的外角和的倍,那么从这个多边形的一个顶点出发的对角线的条数是(
)
A.
B.
C.
D.
8.
将一矩形纸片沿一条直线剪成两个多边形,那么这两个多边形的内角和之和不可能是?
?
?
?
A.
B.
C.
D.
9.
把一个正方形锯掉一个角,剩下的多边形是(
)
A.三角形
B.四边形
C.五边形
D.三角形或四边形或五边形
10.
已知凸边形有条对角线,则此多边形的内角和是?
?
?
?
A.?
B.
C.
D.
11.
从边形的一个顶点出发一共可引条对角线,则这个边形的内角和等于(
)
A.
B.
C.
D.
二、
填空题
12.
六边形的内角和等于________.
13.
一个多边形的每个外角都是,则这个多边形是________边形,它的对角线共有________条.
?14.
正边形每一个外角都是度,则________,它共有________条对角线.
15.
将等边三角形、正方形、正五边形按如图所示的位置摆放,如果,,那么的度数等于________.
三、
解答题
?
16.
为了说明各种三角形之间的关系,小明画了如下结构图:
请你采用类似的方式说明下述几个概念之间的关系:正方形、四边形、梯形、菱形、平行四边形、矩形.
?
17.
在教学活动课中我们学面镶嵌,若给出下面一些边长均为的正三角形、正六边形卡片,要求必须同时使用这两种卡片,不重叠、无缝隙,围绕某一个顶点拼在一起,成一个平面图案,则共拼出多少种不同的图案;其中所拼图案中最大的周长为多少.
?
18.
清晨,小强沿着一个五边形广场周围的小路,按逆时针方向跑步.
(1)小强每从一条街道转到下一条街道时,身体转过的角是哪些角在图上标出它们.
(2)他每跑完一圈,身体转过的角度之和是多少?
(3)在图中,你能求出吗?你是怎样得到的?
(4)如果广场是六边形、八边形的形状,那么还有类似的结论吗?
参考答案与试题解析
一、
选择题
1.
【答案】
C
【解答】
解:∵
多边形的每一个内角都等于,
∴
多边形的每一个外角都等于,
∴
边数.
故选.
2.
【答案】
B
【解答】
此题暂无解答
3.
【答案】
B
【解答】
∵
一个正多边形的每个内角都为,
∴
此多边形的每一个外角是:=,
∴
这个正多边形的边数是:=,
4.
【答案】
B
【解答】
解:多边形内角和定理:且为整数),该公式推导的基本方法是从边形的一个顶点出发引出条对角线,将边形分割为个三角形,这个三角形的所有内角之和正好是边形的内角和,体现了化归思想.
故选.
5.
【答案】
D
【解答】
解:设这个多边形的边数为,
由于多边形中边形的内角和等于,且任意多边形的外角和都为
根据题意可知,
解得
即这个多边形的边数是,
故选.
6.
【答案】
D
【解答】
设多边形的边数是,则
解得:
故选.
7.
【答案】
A
【解答】
解:设这个多边形有条边,由题意得:
,
解得;,
从这个多边形的一个顶点出发的对角线的条数是,
故选:.
8.
【答案】
D
【解答】
解:①将矩形沿对角线剪开,得到两个三角形,
两个多边形的内角和为:=;
②将矩形从一顶点剪向对边,
得到一个三角形和一个四边形,
两个多边形的内角和为:=;
③将矩形沿一组对边剪开,得到两个四边形,
两个多边形的内角和为:=;
④将矩形沿一组邻边剪开,
得到一个三角形和一个五边形,
其内角和为:=.
故选.
9.
【答案】
D
【解答】
解:如图所示:
,
故选:.
10.
【答案】
B
【解答】
解:∵
凸边形有条对角线,
∴
,
解得:(舍去),或,
即多边形的边数是,
∴
这个多边形的内角和.
故选.
11.
【答案】
A
【解答】
解:∵
从边形的一个顶点出发一共可引条对角线,
∴
多边形是边形,
∴
内角和是,
故选.
二、
填空题
12.
【答案】
【解答】
解:边形的内角和是,
则六边形的内角和等于.
故答案为:.
13.
【答案】
六,
【解答】
解:,
,
故答案为:六;.
14.
【答案】
,
【解答】
解:,所以这个正多边形是正八边形.
对角线条数:.
故答案为:;.
15.
【答案】
【解答】
此题暂无解答
三、
解答题
16.
【答案】
解:如图所示:
【解答】
解:如图所示:
17.
【答案】
解:共拼出中不同的图案,如图所示:
由图象可知最大周长为.
【解答】
解:共拼出中不同的图案,如图所示:
由图象可知最大周长为.
18.
【答案】
解:,,,,;
(2)∵
各角是五边形的外角,
∴
身体转过的角度之和是;
(3),
因为各角是五边形的外角;
(4)多边形外角和为度.
【解答】
解:,,,,;
(2)∵
各角是五边形的外角,
∴
身体转过的角度之和是;
(3),
因为各角是五边形的外角;
(4)多边形外角和为度.
