12.1 全等三角形暑期学情跟踪练习2021-2022学年人教版数学八年级上册(word版含答案)
文档属性
| 名称 | 12.1 全等三角形暑期学情跟踪练习2021-2022学年人教版数学八年级上册(word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 132.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-15 21:39:20 | ||
图片预览


文档简介
12.1
全等三角形暑期学情跟踪练习
一、选择题
1.下列说法中,正确的是( )
A.面积相等的两个图形是全等图形
B.形状相等的两个图形是全等图形
C.周长相等的两个图形是全等图形
D.能够完全重合的两个图形是全等图形
2.如图为正方形网格,则∠1+∠2+∠3=( )
A.105°
B.120°
C.115°
D.135°
3.已知图中的两个三角形全等,则∠α等于( )
A.50°
B.60°
C.70°
D.80°
4.下列说法正确的是( )
A.两个等边三角形一定是全等图形
B.两个全等图形面积一定相等
C.形状相同的两个图形一定全等
D.两个正方形一定是全等图形
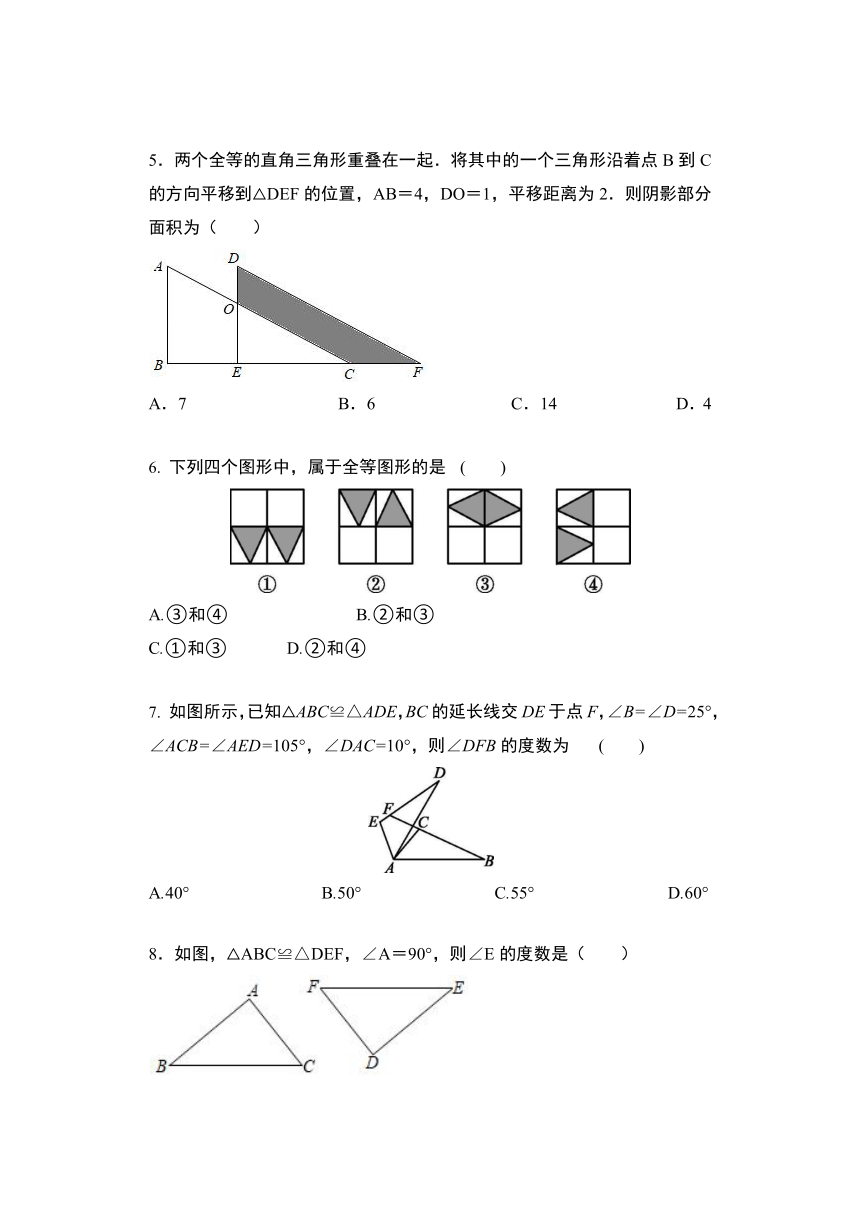
5.两个全等的直角三角形重叠在一起.将其中的一个三角形沿着点B到C的方向平移到△DEF的位置,AB=4,DO=1,平移距离为2.则阴影部分面积为( )
A.7
B.6
C.14
D.4
6.
下列四个图形中,属于全等图形的是
( )
A.③和④
B.②和③
C.①和③
D.②和④
7.
如图所示,已知△ABC≌△ADE,BC的延长线交DE于点F,∠B=∠D=25°,∠ACB=∠AED=105°,∠DAC=10°,则∠DFB的度数为
( )
A.40°
B.50°
C.55°
D.60°
8.如图,△ABC≌△DEF,∠A=90°,则∠E的度数是( )
A.30°
B.40°
C.50°
D.90°
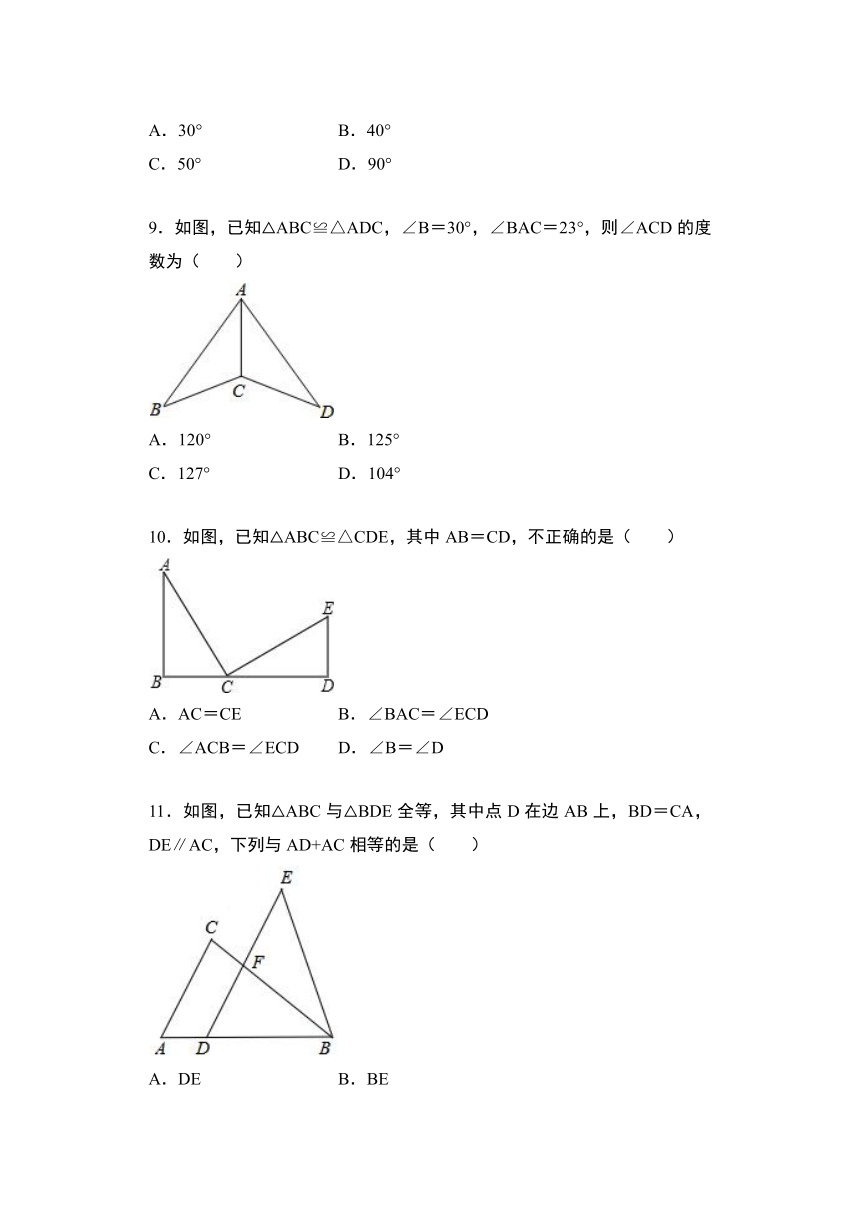
9.如图,已知△ABC≌△ADC,∠B=30°,∠BAC=23°,则∠ACD的度数为( )
A.120°
B.125°
C.127°
D.104°
10.如图,已知△ABC≌△CDE,其中AB=CD,不正确的是( )
A.AC=CE
B.∠BAC=∠ECD
C.∠ACB=∠ECD
D.∠B=∠D
11.如图,已知△ABC与△BDE全等,其中点D在边AB上,BD=CA,DE∥AC,下列与AD+AC相等的是( )
A.DE
B.BE
C.BF
D.DF
二、填空题
12.
如图,已知△ABC≌△ADE,若∠B=42°,∠C=90°,∠EAB=40°,则∠BAD=________°.
13.如图,已知△ABC≌△DEF,且点B与点E对应,点C与点F对应,BE=5,BF=1,则CF=
.
14.
如图,△ABC≌△DEF,根据图中提供的信息,得x=________.
15.如图,已知△ABD≌△ACE,∠A=53°,∠B=22°,则∠C=
°.
16.
已知△ABC≌△DEF,若△ABC的周长为16,AB=6,AC=7,则EF=________.
三、解答题
17.如图所示,A,C,E三点在同一直线上,且△ABC≌△DAE.
(1)求证:BC=DE+CE;
(2)当△ABC满足什么条件时,BC∥DE?
18.
如图所示,在△ABC中,D为BC边上一点,△ABD≌△ACD,∠BAC=90°.
(1)求∠B的度数;
(2)判断AD与BC的位置关系,并说明理由.
19.如图,已知△ABC≌△DEB,点E在AB上,若DE=10,BC=4,∠C=70°.
(1)求线段AE的长.
(2)求∠DBC的度数.
20.如图,点E在AB上,AC与DE相交于点F,∠B=65°.
(1)求∠DCA的度数;
(2)若∠A=20°,求∠DFA的度数.
答案
一、选择题
1.
D
2.
D
3.
C
4.
B
5.
A
6.
D
7.
D
8.
B
9.
C
10.
C
11.
A
二、填空题
12.
88
13.
3
14.
20
15.
22
16.
3
三、解答题
17.
(1)证明:∵△ABC≌△DAE,
∴AE=BC,AC=DE,
又∵AE=AC+CE,
∴BC=DE+CE;
(2)解:∵BC∥DE,
∴∠BCE=∠E,
又∵△ABC≌△DAE,
∴∠ACB=∠E,
∴∠ACB=∠BCE,
又∵∠ACB+∠BCE=180°,
∴∠ACB=90°,
即当△ABC满足∠ACB为直角时,BC∥DE.
18.
解:(1)∵△ABD≌△ACD,∴∠B=∠C.
又∵∠BAC=90°,∴∠B=45°.
(2)AD⊥BC.理由:∵△ABD≌△ACD,
∴∠BDA=∠CDA.
∵∠BDA+∠CDA=180°,
∴∠BDA=∠CDA=90°,即AD⊥BC.
19.
解:(1)∵△ABC≌△DEB,DE=10,
∴AB=DE=10,BE=BC=4,
∴AE=AB﹣BE=6;
(2)∵△ABC≌△DEB,∠D=30°,
∴∠BAC=∠D=30°,∠DBE=∠C=70°,
∴∠ABC=180°﹣30°﹣70°=80°,
∴∠DBC=∠ABC﹣∠DBE=10°.
20.
(1)证明:∵△ABC≌△DEC,
∴CB=CE,∠DCE=∠ACB,
∴∠CEB=∠B=65°,
在△BEC中,∠CEB+∠B+∠ECB=180°,
∴∠ECB=180°﹣65°﹣65°=50°,
又∠DCE=∠ACB,
∴∠DCA=∠ECB=50°;
(2)解:∵△ABC≌△DEC,
∴∠D=∠A=20°,
在△DFC中,
∠DFA=∠DCA+∠D=50°+20°=70°.
试卷第8页,总8页
全等三角形暑期学情跟踪练习
一、选择题
1.下列说法中,正确的是( )
A.面积相等的两个图形是全等图形
B.形状相等的两个图形是全等图形
C.周长相等的两个图形是全等图形
D.能够完全重合的两个图形是全等图形
2.如图为正方形网格,则∠1+∠2+∠3=( )
A.105°
B.120°
C.115°
D.135°
3.已知图中的两个三角形全等,则∠α等于( )
A.50°
B.60°
C.70°
D.80°
4.下列说法正确的是( )
A.两个等边三角形一定是全等图形
B.两个全等图形面积一定相等
C.形状相同的两个图形一定全等
D.两个正方形一定是全等图形
5.两个全等的直角三角形重叠在一起.将其中的一个三角形沿着点B到C的方向平移到△DEF的位置,AB=4,DO=1,平移距离为2.则阴影部分面积为( )
A.7
B.6
C.14
D.4
6.
下列四个图形中,属于全等图形的是
( )
A.③和④
B.②和③
C.①和③
D.②和④
7.
如图所示,已知△ABC≌△ADE,BC的延长线交DE于点F,∠B=∠D=25°,∠ACB=∠AED=105°,∠DAC=10°,则∠DFB的度数为
( )
A.40°
B.50°
C.55°
D.60°
8.如图,△ABC≌△DEF,∠A=90°,则∠E的度数是( )
A.30°
B.40°
C.50°
D.90°
9.如图,已知△ABC≌△ADC,∠B=30°,∠BAC=23°,则∠ACD的度数为( )
A.120°
B.125°
C.127°
D.104°
10.如图,已知△ABC≌△CDE,其中AB=CD,不正确的是( )
A.AC=CE
B.∠BAC=∠ECD
C.∠ACB=∠ECD
D.∠B=∠D
11.如图,已知△ABC与△BDE全等,其中点D在边AB上,BD=CA,DE∥AC,下列与AD+AC相等的是( )
A.DE
B.BE
C.BF
D.DF
二、填空题
12.
如图,已知△ABC≌△ADE,若∠B=42°,∠C=90°,∠EAB=40°,则∠BAD=________°.
13.如图,已知△ABC≌△DEF,且点B与点E对应,点C与点F对应,BE=5,BF=1,则CF=
.
14.
如图,△ABC≌△DEF,根据图中提供的信息,得x=________.
15.如图,已知△ABD≌△ACE,∠A=53°,∠B=22°,则∠C=
°.
16.
已知△ABC≌△DEF,若△ABC的周长为16,AB=6,AC=7,则EF=________.
三、解答题
17.如图所示,A,C,E三点在同一直线上,且△ABC≌△DAE.
(1)求证:BC=DE+CE;
(2)当△ABC满足什么条件时,BC∥DE?
18.
如图所示,在△ABC中,D为BC边上一点,△ABD≌△ACD,∠BAC=90°.
(1)求∠B的度数;
(2)判断AD与BC的位置关系,并说明理由.
19.如图,已知△ABC≌△DEB,点E在AB上,若DE=10,BC=4,∠C=70°.
(1)求线段AE的长.
(2)求∠DBC的度数.
20.如图,点E在AB上,AC与DE相交于点F,∠B=65°.
(1)求∠DCA的度数;
(2)若∠A=20°,求∠DFA的度数.
答案
一、选择题
1.
D
2.
D
3.
C
4.
B
5.
A
6.
D
7.
D
8.
B
9.
C
10.
C
11.
A
二、填空题
12.
88
13.
3
14.
20
15.
22
16.
3
三、解答题
17.
(1)证明:∵△ABC≌△DAE,
∴AE=BC,AC=DE,
又∵AE=AC+CE,
∴BC=DE+CE;
(2)解:∵BC∥DE,
∴∠BCE=∠E,
又∵△ABC≌△DAE,
∴∠ACB=∠E,
∴∠ACB=∠BCE,
又∵∠ACB+∠BCE=180°,
∴∠ACB=90°,
即当△ABC满足∠ACB为直角时,BC∥DE.
18.
解:(1)∵△ABD≌△ACD,∴∠B=∠C.
又∵∠BAC=90°,∴∠B=45°.
(2)AD⊥BC.理由:∵△ABD≌△ACD,
∴∠BDA=∠CDA.
∵∠BDA+∠CDA=180°,
∴∠BDA=∠CDA=90°,即AD⊥BC.
19.
解:(1)∵△ABC≌△DEB,DE=10,
∴AB=DE=10,BE=BC=4,
∴AE=AB﹣BE=6;
(2)∵△ABC≌△DEB,∠D=30°,
∴∠BAC=∠D=30°,∠DBE=∠C=70°,
∴∠ABC=180°﹣30°﹣70°=80°,
∴∠DBC=∠ABC﹣∠DBE=10°.
20.
(1)证明:∵△ABC≌△DEC,
∴CB=CE,∠DCE=∠ACB,
∴∠CEB=∠B=65°,
在△BEC中,∠CEB+∠B+∠ECB=180°,
∴∠ECB=180°﹣65°﹣65°=50°,
又∠DCE=∠ACB,
∴∠DCA=∠ECB=50°;
(2)解:∵△ABC≌△DEC,
∴∠D=∠A=20°,
在△DFC中,
∠DFA=∠DCA+∠D=50°+20°=70°.
试卷第8页,总8页
