四川省安岳县高中2022届高三上学期7月检测理科数学试题 Word版含答案
文档属性
| 名称 | 四川省安岳县高中2022届高三上学期7月检测理科数学试题 Word版含答案 |  | |
| 格式 | docx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-15 18:05:38 | ||
图片预览




文档简介
安岳县高中2022届高三上学期7月检测
理科数学
注意事项:
1.答题前,考生务必将自己的姓名、考号填写在答题卡上,并将条形码贴
在答题卡上对应的虚线框内。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案
标号涂黑。如需改动,用橡皮擦干净后,再选涂其它答案标号。回答非选择题时,
将答案写在答题卡上。写在本试卷上无效。
考试结束后,将答题卡交回。
选择题:本题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。
方程组的解集是
A. B.
C. D. 或
命题“,使是”的否定是
A. ,使得 B. ,使得.
C. ,使得 D. ,使得
某学校共有教职工120人,对他们进行年龄结构和受教育程度的调查,其结果如下表:现从该校教职工中任取1人,则下列结论正确的是
本科
研究生
合计
35岁以下
40
30
70
岁
27
13
40
50岁以上
8
2
10
A. 该教职工具有本科学历的概率低于
B. 该教职工具有研究生学历的概率超过
C. 该教职工的年龄在50岁以上的概率超过
D. 该教职工的年龄在35岁及以上且具有研究生学历的概率超过
为加强环境保护,治理空气污染,某环保部门对辖区内一工厂产生的废气进行了监测,发现该厂产生的废气经过过滤后排放,过滤过程中废气的污染物数量与时间的关系为如果在前5个小时消除了的污染物,那么污染物减少需要花的时间为
A. 7小时 B. 10小时 C. 15小时 D. 18小时
已知椭圆C的方程是,点在椭圆C上,过点A且斜率为的直线恰好经过椭圆的一个焦点,则椭圆C的方程为
4883785396240A. B. C. D.
如图所示,网格纸上的小正方形的边长为1,图中粗线的是某几何体的三视图,则该几何体的体积为
A. B.
C. D.
已知正整数数列满足若,
A. 1 B. 2 C. 3 D. 4
点P为边长为1的正四面体ABCD底面BCD内一点,且直线AP与底面BCD所成角的正切值为,则动点P所在曲线长度为
A. B. C. D.
已知,则
A. B. C. 2 D. 3
某校开展“迎奥运阳光体育”活动,共设踢毽、跳绳、拔河、推火车、多人多足五个集体比赛项目,各比赛项目逐一进行为了增强比赛的趣味性,在安排比赛顺序时,多人多足不排在第一场,拔河排在最后一场,则不同的安排方案种数为
A. 3 B. 18 C. 21 D. 24
中,,,,点O为的外心,若,则实数的值为
A. 7 B. C. D.
某市在精准扶贫专项工作中,通过实施农村农田水利项目,以夯实农村农业的发展基础,助力脱贫攻坚现计划对该村旧的灌溉水渠进行加固改造,已知旧水渠的横截面是一段抛物线弧如图所示,顶点O在水渠的最底端,渠宽AB为3m,渠深为1m,欲在旧水渠内填充混凝土加固,改造成横截面为等腰梯形的新水渠,且新水渠底面与地面平行不改变渠宽,若要使所填充的混凝土量最小,则新水渠的底宽为
46170851023620center0A. B. 1m C. D. 2m
填空题:本题共4小题,每小题5分,共20分。
_________.
若AD是的中线,已知,,若为基底,则????????????????????.
已知双曲线与椭圆有相同的焦点,则实数
已知函数,,若,,则的最小值为______ .
解答题:共70分。解答应写出文字说明、证明过程或演算步骤。第17~21题为必考题,每个试题考生都必须作答。第22、23题为选考题,考生根据要求作答。
(一)必考题:共60分。
设数列的前n项和,为等比数列,且,.
求数列和的通项公式;
求数列的前n项和.
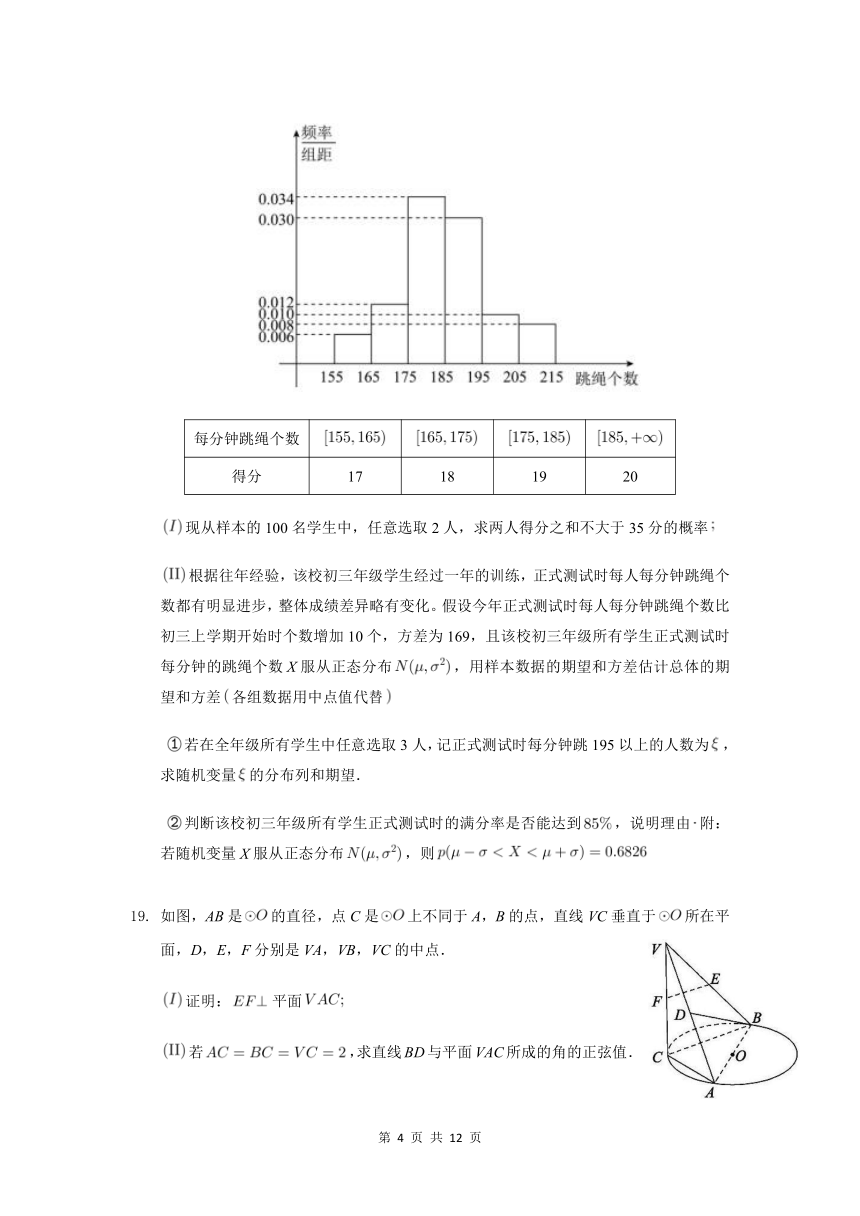
2020年10月,中共中央办公厅、国务院办公厅印发了关于全面加强和改进新时代学校体育工作的意见,某地积极开展中小学健康促进活动,决定在2021年体育中考中再增加一定的分数,规定:考生需参加游泳、长跑、一分钟跳绳三项测试,其中一分钟跳绳满分20分,某校在初三上学期开始要掌握全年级学生一分钟跳绳情况,随机抽取了100名学生进行测试,得到如图所示频率分布直方图,且规定计分规则如下表:
每分钟跳绳个数
得分
17
18
19
20
现从样本的100名学生中,任意选取2人,求两人得分之和不大于35分的概率
根据往年经验,该校初三年级学生经过一年的训练,正式测试时每人每分钟跳绳个数都有明显进步,整体成绩差异略有变化。假设今年正式测试时每人每分钟跳绳个数比初三上学期开始时个数增加10个,方差为169,且该校初三年级所有学生正式测试时每分钟的跳绳个数X服从正态分布,用样本数据的期望和方差估计总体的期望和方差各组数据用中点值代替
若在全年级所有学生中任意选取3人,记正式测试时每分钟跳195以上的人数为,求随机变量的分布列和期望.
判断该校初三年级所有学生正式测试时的满分率是否能达到,说明理由附:若随机变量X服从正态分布,则
4552950360045如图,AB是的直径,点C是上不同于A,B的点,直线VC垂直于所在平面,D,E,F分别是VA,VB,VC的中点.
证明:平面
若,求直线BD与平面VAC所成的角的正弦值.
4581525371475如图,已知点,,以线段为直径的圆内切于圆O:,点G的轨迹为E.
Ⅰ求点G的轨迹E的方程;
Ⅱ轨迹E与y轴正半轴交于点A,是否存在直线l与轨迹E交于M,N两点,使得点为的垂心,若存在,求出直线l的方程;若不存在,说明理由.
已知函数.
若恒成立,求实数a的取值范围.
若函数的两个零点为,,证明:.
(二)选考题:共10分。请考生在第22、23题中任选一题作答。如果多做,则按所做的第一题计分。
在直角坐标系xOy中,曲线C的参数方程为为参数以O为极点,x轴的正半轴为极轴建立极坐标系,直线l的极坐标方程为
求曲线C的普通方程和直线l的直角坐标方程
在曲线C上任取一点,保持纵坐标y不变,将横坐标x伸长为原来的倍得到曲线设直线l与曲线相交于M,N两点,点,求的值
在数列中,,.
分别计算,,的值;
由猜想出数列的通项公式,并用数学归纳法加以证明.
安岳县高中2022届高三上学期7月检测
理科数学答案
选择题答案
一、选择题
1.C 2.D 3.D 4.B
5.D 6.B 7.D 8.C
9.B 10.B 11.A 12.B
非选择题答案
二、填空题
13. 14. 15. 16.
三、解答题
17.解:数列的前n项和,
当时,,
得:,
,
,,,
,
.
由等比数列前n项和公式可得.
18.解:设选取两人得分之和不大于35分,为事件A,
则事件A的基本事件总数为,
由题意可得:得17分的学生人数为人,
得18分的学生人数为人,
事件A发生包含两种可能:一种是两人得分均为17分,一种是两人中一人得17分,一人得18分,
所以事件A的基本事件个数为,
所以事件A的概率;
个,
所以正式测试时,,
则,所以,
所以,
由正态分布模型,全年级所有学生中任取1人,
每分钟跳绳个数195以上的概率为,
即,
,
,
,
,
所以的分布列为:
0
1
2
3
P
所以
由,
所以
所以预测正式测试时每分钟跳绳个数在182个以上的人数比例为,
由题意每分钟跳绳个数不少于185个才能得到满分,
因此可以预测该校初三年级所有学生正式测试时的满分率,因此不能达到.
4248150224409019.解:证明:因为直线VC垂直于所在平面ABC,且平面ABC
所以.
因为AB是的直径,点C在上,
所以.
又,AC,平面VAC,
所以平面VAC.
因为E,F分别是VB,VC的中点,所以,
所以平面VAC.
由知,平面VAC.
连接CD,则为直线BD与平面VAC所成的角.
因为,所以.
又D是VA的中点,所以等边中.
因为平面VAC,平面VAC,
所以.
所以.
所以直线BD与平面VAC所成的角的正弦值为.
20.解:记线段的中点为H,由于线段的中点为O,连接OH,则,,
设的半径为r,与内切于Q,连接HQ,则O,H,Q三点共线,
于是.
又,根据椭圆的定义可得E的方程为.
假设存在满足条件的直线l,由,,知直线斜率为,
于是由知直线l的斜率为1,设直线l的方程为,
由消去y得,
设点,,根据韦达定理得,,
由知,因为,,
所以
,
解得舍或,
因此所求得直线l的方程为.
21.解:解:因为恒成立,所以,
即恒成立.
令,则,
易知在上单调递增,且.
所以当时,当时,.
所以在上单调递减,在上单调递增,
所以,故
证明:由题意可知方程的两根为,.
令,则的两个零点为,.
.
当时,,在上单调递增,不存在两个零点
当时,在上单调递增,在上单调递减,
则,得.
设,则,
因为,所以,.
要证,即要证,即证.
令
,
则,所以在上单调递减,所以.
因为,所以.
因为,,且在上单调递减,
所以,即,故成立.
22.解:由曲线C的参数方程,消去参数,得曲线C的普通方程为.
,,直线l的直角坐标方程为.
I设曲线C上任一点经坐标变换后对应的点为.
据题意,得即
,,即曲线的普通方程为.
直线l过定点,
直线l的参数方程为为参数.
将直线l的参数方程代入曲线的普通方程,
整理可得.
.
设,为方程的两个实数根,
则,.
.
22.解:曲线的参数方程为为参数,
的普通方程为.
直线l的极坐标方程为,即.
由,得直线l的直角坐标方程.
直线l的参数方程为为参数,
代入的普通方程,得.
设A,B两点对应的参数分别为,,.
23.解:令,
,
,
,.
,.
又,
,,;
由猜得,
证明:当时结论成立;
假设当时成立,即,
则当时,,
即当时,结论也成立,
综合得,成立.
理科数学
注意事项:
1.答题前,考生务必将自己的姓名、考号填写在答题卡上,并将条形码贴
在答题卡上对应的虚线框内。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案
标号涂黑。如需改动,用橡皮擦干净后,再选涂其它答案标号。回答非选择题时,
将答案写在答题卡上。写在本试卷上无效。
考试结束后,将答题卡交回。
选择题:本题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。
方程组的解集是
A. B.
C. D. 或
命题“,使是”的否定是
A. ,使得 B. ,使得.
C. ,使得 D. ,使得
某学校共有教职工120人,对他们进行年龄结构和受教育程度的调查,其结果如下表:现从该校教职工中任取1人,则下列结论正确的是
本科
研究生
合计
35岁以下
40
30
70
岁
27
13
40
50岁以上
8
2
10
A. 该教职工具有本科学历的概率低于
B. 该教职工具有研究生学历的概率超过
C. 该教职工的年龄在50岁以上的概率超过
D. 该教职工的年龄在35岁及以上且具有研究生学历的概率超过
为加强环境保护,治理空气污染,某环保部门对辖区内一工厂产生的废气进行了监测,发现该厂产生的废气经过过滤后排放,过滤过程中废气的污染物数量与时间的关系为如果在前5个小时消除了的污染物,那么污染物减少需要花的时间为
A. 7小时 B. 10小时 C. 15小时 D. 18小时
已知椭圆C的方程是,点在椭圆C上,过点A且斜率为的直线恰好经过椭圆的一个焦点,则椭圆C的方程为
4883785396240A. B. C. D.
如图所示,网格纸上的小正方形的边长为1,图中粗线的是某几何体的三视图,则该几何体的体积为
A. B.
C. D.
已知正整数数列满足若,
A. 1 B. 2 C. 3 D. 4
点P为边长为1的正四面体ABCD底面BCD内一点,且直线AP与底面BCD所成角的正切值为,则动点P所在曲线长度为
A. B. C. D.
已知,则
A. B. C. 2 D. 3
某校开展“迎奥运阳光体育”活动,共设踢毽、跳绳、拔河、推火车、多人多足五个集体比赛项目,各比赛项目逐一进行为了增强比赛的趣味性,在安排比赛顺序时,多人多足不排在第一场,拔河排在最后一场,则不同的安排方案种数为
A. 3 B. 18 C. 21 D. 24
中,,,,点O为的外心,若,则实数的值为
A. 7 B. C. D.
某市在精准扶贫专项工作中,通过实施农村农田水利项目,以夯实农村农业的发展基础,助力脱贫攻坚现计划对该村旧的灌溉水渠进行加固改造,已知旧水渠的横截面是一段抛物线弧如图所示,顶点O在水渠的最底端,渠宽AB为3m,渠深为1m,欲在旧水渠内填充混凝土加固,改造成横截面为等腰梯形的新水渠,且新水渠底面与地面平行不改变渠宽,若要使所填充的混凝土量最小,则新水渠的底宽为
46170851023620center0A. B. 1m C. D. 2m
填空题:本题共4小题,每小题5分,共20分。
_________.
若AD是的中线,已知,,若为基底,则????????????????????.
已知双曲线与椭圆有相同的焦点,则实数
已知函数,,若,,则的最小值为______ .
解答题:共70分。解答应写出文字说明、证明过程或演算步骤。第17~21题为必考题,每个试题考生都必须作答。第22、23题为选考题,考生根据要求作答。
(一)必考题:共60分。
设数列的前n项和,为等比数列,且,.
求数列和的通项公式;
求数列的前n项和.
2020年10月,中共中央办公厅、国务院办公厅印发了关于全面加强和改进新时代学校体育工作的意见,某地积极开展中小学健康促进活动,决定在2021年体育中考中再增加一定的分数,规定:考生需参加游泳、长跑、一分钟跳绳三项测试,其中一分钟跳绳满分20分,某校在初三上学期开始要掌握全年级学生一分钟跳绳情况,随机抽取了100名学生进行测试,得到如图所示频率分布直方图,且规定计分规则如下表:
每分钟跳绳个数
得分
17
18
19
20
现从样本的100名学生中,任意选取2人,求两人得分之和不大于35分的概率
根据往年经验,该校初三年级学生经过一年的训练,正式测试时每人每分钟跳绳个数都有明显进步,整体成绩差异略有变化。假设今年正式测试时每人每分钟跳绳个数比初三上学期开始时个数增加10个,方差为169,且该校初三年级所有学生正式测试时每分钟的跳绳个数X服从正态分布,用样本数据的期望和方差估计总体的期望和方差各组数据用中点值代替
若在全年级所有学生中任意选取3人,记正式测试时每分钟跳195以上的人数为,求随机变量的分布列和期望.
判断该校初三年级所有学生正式测试时的满分率是否能达到,说明理由附:若随机变量X服从正态分布,则
4552950360045如图,AB是的直径,点C是上不同于A,B的点,直线VC垂直于所在平面,D,E,F分别是VA,VB,VC的中点.
证明:平面
若,求直线BD与平面VAC所成的角的正弦值.
4581525371475如图,已知点,,以线段为直径的圆内切于圆O:,点G的轨迹为E.
Ⅰ求点G的轨迹E的方程;
Ⅱ轨迹E与y轴正半轴交于点A,是否存在直线l与轨迹E交于M,N两点,使得点为的垂心,若存在,求出直线l的方程;若不存在,说明理由.
已知函数.
若恒成立,求实数a的取值范围.
若函数的两个零点为,,证明:.
(二)选考题:共10分。请考生在第22、23题中任选一题作答。如果多做,则按所做的第一题计分。
在直角坐标系xOy中,曲线C的参数方程为为参数以O为极点,x轴的正半轴为极轴建立极坐标系,直线l的极坐标方程为
求曲线C的普通方程和直线l的直角坐标方程
在曲线C上任取一点,保持纵坐标y不变,将横坐标x伸长为原来的倍得到曲线设直线l与曲线相交于M,N两点,点,求的值
在数列中,,.
分别计算,,的值;
由猜想出数列的通项公式,并用数学归纳法加以证明.
安岳县高中2022届高三上学期7月检测
理科数学答案
选择题答案
一、选择题
1.C 2.D 3.D 4.B
5.D 6.B 7.D 8.C
9.B 10.B 11.A 12.B
非选择题答案
二、填空题
13. 14. 15. 16.
三、解答题
17.解:数列的前n项和,
当时,,
得:,
,
,,,
,
.
由等比数列前n项和公式可得.
18.解:设选取两人得分之和不大于35分,为事件A,
则事件A的基本事件总数为,
由题意可得:得17分的学生人数为人,
得18分的学生人数为人,
事件A发生包含两种可能:一种是两人得分均为17分,一种是两人中一人得17分,一人得18分,
所以事件A的基本事件个数为,
所以事件A的概率;
个,
所以正式测试时,,
则,所以,
所以,
由正态分布模型,全年级所有学生中任取1人,
每分钟跳绳个数195以上的概率为,
即,
,
,
,
,
所以的分布列为:
0
1
2
3
P
所以
由,
所以
所以预测正式测试时每分钟跳绳个数在182个以上的人数比例为,
由题意每分钟跳绳个数不少于185个才能得到满分,
因此可以预测该校初三年级所有学生正式测试时的满分率,因此不能达到.
4248150224409019.解:证明:因为直线VC垂直于所在平面ABC,且平面ABC
所以.
因为AB是的直径,点C在上,
所以.
又,AC,平面VAC,
所以平面VAC.
因为E,F分别是VB,VC的中点,所以,
所以平面VAC.
由知,平面VAC.
连接CD,则为直线BD与平面VAC所成的角.
因为,所以.
又D是VA的中点,所以等边中.
因为平面VAC,平面VAC,
所以.
所以.
所以直线BD与平面VAC所成的角的正弦值为.
20.解:记线段的中点为H,由于线段的中点为O,连接OH,则,,
设的半径为r,与内切于Q,连接HQ,则O,H,Q三点共线,
于是.
又,根据椭圆的定义可得E的方程为.
假设存在满足条件的直线l,由,,知直线斜率为,
于是由知直线l的斜率为1,设直线l的方程为,
由消去y得,
设点,,根据韦达定理得,,
由知,因为,,
所以
,
解得舍或,
因此所求得直线l的方程为.
21.解:解:因为恒成立,所以,
即恒成立.
令,则,
易知在上单调递增,且.
所以当时,当时,.
所以在上单调递减,在上单调递增,
所以,故
证明:由题意可知方程的两根为,.
令,则的两个零点为,.
.
当时,,在上单调递增,不存在两个零点
当时,在上单调递增,在上单调递减,
则,得.
设,则,
因为,所以,.
要证,即要证,即证.
令
,
则,所以在上单调递减,所以.
因为,所以.
因为,,且在上单调递减,
所以,即,故成立.
22.解:由曲线C的参数方程,消去参数,得曲线C的普通方程为.
,,直线l的直角坐标方程为.
I设曲线C上任一点经坐标变换后对应的点为.
据题意,得即
,,即曲线的普通方程为.
直线l过定点,
直线l的参数方程为为参数.
将直线l的参数方程代入曲线的普通方程,
整理可得.
.
设,为方程的两个实数根,
则,.
.
22.解:曲线的参数方程为为参数,
的普通方程为.
直线l的极坐标方程为,即.
由,得直线l的直角坐标方程.
直线l的参数方程为为参数,
代入的普通方程,得.
设A,B两点对应的参数分别为,,.
23.解:令,
,
,
,.
,.
又,
,,;
由猜得,
证明:当时结论成立;
假设当时成立,即,
则当时,,
即当时,结论也成立,
综合得,成立.
同课章节目录
