五年级下册数学课件-1.1 圆的认识 青岛版(五四学制)(共40张PPT)
文档属性
| 名称 | 五年级下册数学课件-1.1 圆的认识 青岛版(五四学制)(共40张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 6.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版(五四制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-16 00:00:00 | ||
图片预览










文档简介
(共40张PPT)
圆的认识
你能说一说在生活中我们见到的圆吗?
下
上
封面
目录
退出
封底
以前学过的图形都是由几条线段所围成的封闭平面图形。
圆是由曲线所围成的封闭平面图形。
圆和以前学过的图形有什么不同?
圆是由封闭曲线围成的平面图形
请同学们拿出桌面的圆,再次闭上眼睛摸一摸圆的边,想象一下圆的形状。
你能借助你手头的物体或工具,想办法画一个圆吗?
看谁画的又快又好
上面这两种方法都是借助实物画圆。
缺点是只能画出形状,尺寸不好把握。
今天我们来学习用圆规画圆。
你们会用圆规画圆啊?
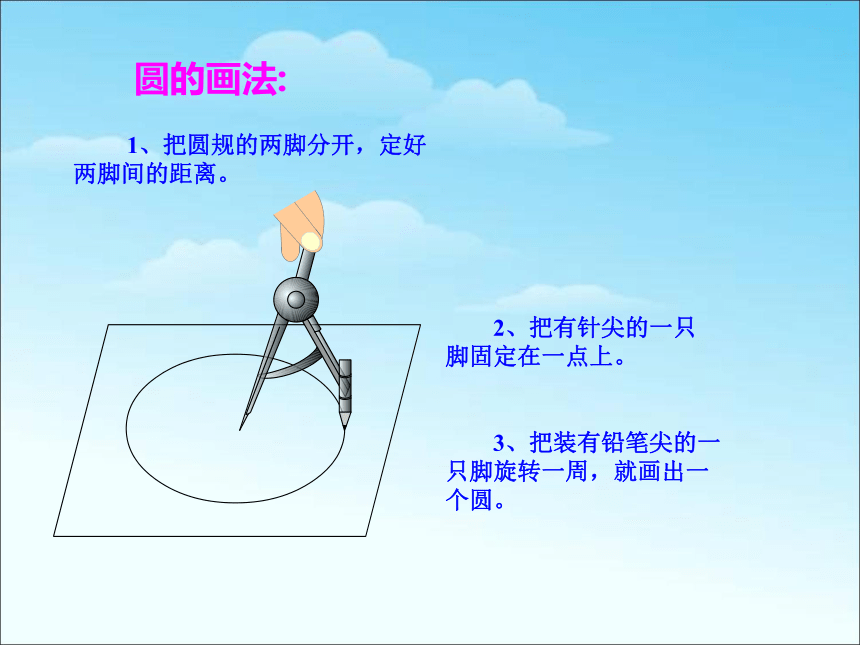
圆的画法:
1、把圆规的两脚分开,定好两脚间的距离。
2、把有针尖的一只脚固定在一点上。
3、把装有铅笔尖的一只脚旋转一周,就画出一个圆。
那你们还想认识圆各部分的名称吗?
请大家自学课本第57页内容,把重点内容画出来。
直径
半径
圆心
:圆中心的一点叫圆心。
:连接圆心和圆上任意一点的线段叫做半径。
:通过圆心并且两端都在圆上的线段叫做直径。
请在自己画好的圆中,标出圆心、半径、直径,并用字母表示出来。
认识圆的圆心、半径和直径
连接圆心和圆上任意一点的线段叫做半径。
通过圆心并且两端都在圆上的线段叫做直径。
·
O
圆心
半径r
直径d
1、圆的中心位置是由什么决定的,圆心决定圆的什么?半径决定圆的什么?
2、圆规两脚之间的距离是什么?
思考
那同一个圆里,半径、直径还有什么特征?半径、直径还有怎样的关系?圆还有什么特征?
拿出你们准备的圆,沿着直径折一折,画一画,量一量,小组4人讨论交流,看你们有什么发现?
活动要求
折一折
折过若干次后,可以发现什么?
同一圆内,所有的半径都相等,所有的直径都相等,直径的长度是半径长度的2倍。圆是轴对称图形,它有无数条对称轴,每一条对称轴都是直径所在的直线
o
?
在同一个圆里,有(
)条半径,
它们的长度都( )
无数
相等
半径的特征:
我国是世界上最早研究圆的国家,早在2000多年前,我国的墨子作出了圆的概念:
“圆,
一中同长也
”
。
这个定义比希腊数学家欧几里得给圆下定义要早1000多年。
墨子
圆心到圆上任意一点的距离都相等。
o
?
在同一个圆里,有( )条直径,
它们的长度都( )
无数
相等
o
?
d
r
r
半径与直径的关系:
o
?
d
r
r
r
半径与直径的关系:
o
?
d
r
r
r
半径与直径的关系:
o
?
d
r
r
d=r+r
d=2r
r=
在同一个圆里,直径是半径的2倍,半径是直径的一半。
半径与直径的关系:
2
1
d
圆是轴对称图形,它有无数条对称轴。
o
对称轴是直径所在的直线。
圆的特征:
o
C
D
G
H
M
N
B
F
E
图中哪些是半径?哪些是直径?哪些不是,为什么?
判
断:
(1)在同一圆内只能画100条直径。
(
)
(2)直径都相等。
(
)
(3)两端都在圆上的线段叫做直径。
(
)
(4)从圆心到圆上任意一点的距离
都相等。
(
)
(5)画一个直径4厘米的圆,圆规两
脚间的距离应该是4厘米。
(
)
(6)直径是半径的2倍
。
(
)
半径(r)
2分米
5厘米
1.42厘米
直径(d)
6米
0.24米
口答:
4分米
3米
10厘米
0.12米
2.84厘米
选
择
题:
(1)画圆时,圆规两脚间的距离是
(
)
A
半径长度
B
直径长度
(2)从圆心到(
)任意一点的线段叫半径。
A
圆心
B
圆外
C
圆上
(3)通过圆心,并且两端都在圆上的(
)
叫直径。
A
直径
B
线段
C
射线
A
C
B
我的收获
(1)今天我学习了圆的知识。我知
道用O表示(
),用r表示
(
),用d表示(
)。直
径和半径的关系是(
)。
(2)我还学会了画圆。画圆时圆规两脚分开的距离是(
),针尖一脚固定的一点是(
)。
半径
r
直
径
d
圆心
半径
直径
d=2r或
r
=
2
d
圆心
半径
返
回
2000多年前,伟大的古希腊数学家毕达哥拉斯在研究完大量的平面图形后,发出这样的感慨:在一切平面图形中,圆最美。而且,2000多年过去了,这一观点得到了越来越多的数学家乃至普通大众的认可。
用圆设计美丽的图案。
圆的认识
你能说一说在生活中我们见到的圆吗?
下
上
封面
目录
退出
封底
以前学过的图形都是由几条线段所围成的封闭平面图形。
圆是由曲线所围成的封闭平面图形。
圆和以前学过的图形有什么不同?
圆是由封闭曲线围成的平面图形
请同学们拿出桌面的圆,再次闭上眼睛摸一摸圆的边,想象一下圆的形状。
你能借助你手头的物体或工具,想办法画一个圆吗?
看谁画的又快又好
上面这两种方法都是借助实物画圆。
缺点是只能画出形状,尺寸不好把握。
今天我们来学习用圆规画圆。
你们会用圆规画圆啊?
圆的画法:
1、把圆规的两脚分开,定好两脚间的距离。
2、把有针尖的一只脚固定在一点上。
3、把装有铅笔尖的一只脚旋转一周,就画出一个圆。
那你们还想认识圆各部分的名称吗?
请大家自学课本第57页内容,把重点内容画出来。
直径
半径
圆心
:圆中心的一点叫圆心。
:连接圆心和圆上任意一点的线段叫做半径。
:通过圆心并且两端都在圆上的线段叫做直径。
请在自己画好的圆中,标出圆心、半径、直径,并用字母表示出来。
认识圆的圆心、半径和直径
连接圆心和圆上任意一点的线段叫做半径。
通过圆心并且两端都在圆上的线段叫做直径。
·
O
圆心
半径r
直径d
1、圆的中心位置是由什么决定的,圆心决定圆的什么?半径决定圆的什么?
2、圆规两脚之间的距离是什么?
思考
那同一个圆里,半径、直径还有什么特征?半径、直径还有怎样的关系?圆还有什么特征?
拿出你们准备的圆,沿着直径折一折,画一画,量一量,小组4人讨论交流,看你们有什么发现?
活动要求
折一折
折过若干次后,可以发现什么?
同一圆内,所有的半径都相等,所有的直径都相等,直径的长度是半径长度的2倍。圆是轴对称图形,它有无数条对称轴,每一条对称轴都是直径所在的直线
o
?
在同一个圆里,有(
)条半径,
它们的长度都( )
无数
相等
半径的特征:
我国是世界上最早研究圆的国家,早在2000多年前,我国的墨子作出了圆的概念:
“圆,
一中同长也
”
。
这个定义比希腊数学家欧几里得给圆下定义要早1000多年。
墨子
圆心到圆上任意一点的距离都相等。
o
?
在同一个圆里,有( )条直径,
它们的长度都( )
无数
相等
o
?
d
r
r
半径与直径的关系:
o
?
d
r
r
r
半径与直径的关系:
o
?
d
r
r
r
半径与直径的关系:
o
?
d
r
r
d=r+r
d=2r
r=
在同一个圆里,直径是半径的2倍,半径是直径的一半。
半径与直径的关系:
2
1
d
圆是轴对称图形,它有无数条对称轴。
o
对称轴是直径所在的直线。
圆的特征:
o
C
D
G
H
M
N
B
F
E
图中哪些是半径?哪些是直径?哪些不是,为什么?
判
断:
(1)在同一圆内只能画100条直径。
(
)
(2)直径都相等。
(
)
(3)两端都在圆上的线段叫做直径。
(
)
(4)从圆心到圆上任意一点的距离
都相等。
(
)
(5)画一个直径4厘米的圆,圆规两
脚间的距离应该是4厘米。
(
)
(6)直径是半径的2倍
。
(
)
半径(r)
2分米
5厘米
1.42厘米
直径(d)
6米
0.24米
口答:
4分米
3米
10厘米
0.12米
2.84厘米
选
择
题:
(1)画圆时,圆规两脚间的距离是
(
)
A
半径长度
B
直径长度
(2)从圆心到(
)任意一点的线段叫半径。
A
圆心
B
圆外
C
圆上
(3)通过圆心,并且两端都在圆上的(
)
叫直径。
A
直径
B
线段
C
射线
A
C
B
我的收获
(1)今天我学习了圆的知识。我知
道用O表示(
),用r表示
(
),用d表示(
)。直
径和半径的关系是(
)。
(2)我还学会了画圆。画圆时圆规两脚分开的距离是(
),针尖一脚固定的一点是(
)。
半径
r
直
径
d
圆心
半径
直径
d=2r或
r
=
2
d
圆心
半径
返
回
2000多年前,伟大的古希腊数学家毕达哥拉斯在研究完大量的平面图形后,发出这样的感慨:在一切平面图形中,圆最美。而且,2000多年过去了,这一观点得到了越来越多的数学家乃至普通大众的认可。
用圆设计美丽的图案。
