2.6.1 有理数的加减混合运算同步练习(含答案)
文档属性
| 名称 | 2.6.1 有理数的加减混合运算同步练习(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 407.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-24 20:26:23 | ||
图片预览



文档简介
21世纪教育网
–全国领先的中小学教育资源及组卷应用平台
北师大版2021–2022学年度七年级数学上册第二章有理数及其运算
2.6
有理数的加减混合运算
第一课时
有理数的加减混合运算(1)
【知识清单】
一、有理数的加减混合运算:
1、有理数加减混合运算即一个算式中既有加法同时也有减法.
2、有理数的加减法混合运算的一般步骤:①在一个算式中,若有减法,应由有理数的减法法则转化为加法;②利用加法则,加法交换律、结合律简化计算.
二、有理数减法运算时注意两“变”:
①改变运算符号;②改变减数的性质符号(变为相反数)
【经典例题】
例题1、计算:
(–2.5)–
()+
【考点】有理数的加减混合运算.
【分析】在一个加减混合运算的算式中,有加法也有减法,应该根据有理数的减法法则把减法转化为加法,然后再按有理数加法法则进行运算.
【解答】(1)原式=
()+
()+(+)
=(–2)+(+3)+(+4)+()+
()+(+)
=5+=.
【点评】该题考查了学生加减混合运算的能力,在一个加减混合运算的算式中,,有理数减法运算的两变一算:(1)一变:把减号边变为加号;(2)二变:变减数为减数的相反数(分清运算符号和性质符号);(3)三算:运用有理数加法的法则进行计算,求出结果.
例题2、数学活动课上,王老师给同学们出了一道题:规定一种新运算“☆”,对于任意有理数a和b,有a☆b=
b–a+5,根据新运算,计算(–3☆2)☆(–4)的值是
.
【考点】有理数的混合运算.?
【分析】根据题中给出的a☆b=
b–a+5列出代数式,进行计算即可.
【解答】原式=[2–
(–3)+5]☆(–4)
=10☆(–4)
=–4–
(+10)+5
=–9.
答案为:9.
【点评】本题考查的是有理数的混合运算,熟知有理数混合运算的法则和正确套入新运算“☆”是解答此题的关键.
【夯实基础】
1、某天海口温度是零上31℃,而黑龙江漠河的温度是零下29℃,海口比漠河温度高出(
)
A.–2℃
B.2℃
C.60℃
D.–60℃
2、计算的值为(
)
A.
B.
C.
D.
3、某运动员在东西走向的公路上练习跑步,跑步情况记录如下(向东为正,单位:米):1000,–1200,
1100,–800,1400,该运动员跑的路程共为( )
A.1500米
B.5500米
C.4500米
D.3700米
4、计算(–4)–(+2)+
(–6)–(–4)的结果是(
)
A.
–4
B.–12
C.–10
D.–8
5、已知|a|=2,|b|=4,|c|=7,且a>b>c,则a–b+c=
.
6、–12,+8,–5的和比它们绝对值的和小
.
7、找规律填数:
(1)
3,4,7,11,18,39,
,
;
(2)
2,5,10,17,
,
;
(3)
6,3,8,5,10,7,12,9,
,
;
(4)
1,3,7,15,31,
,127,225.
8、计算:
(1)18+22+
(26)(8);
(2)
21(15)(+25)11;
(3)
;
(4).
9、把–1,–2,–3,–4,–5,–6,–7,–8,–9,分别填在下面的方格中,使每一横行,每一竖行和每一斜行上的数相加都得–15.
【提优特训】
10、若a+b+c=0,则下列结论正确的是
A.a=b=c=0
B.a,b,c中至少有两个负数
C.a,b,c中至少有两个互为相反数
D.a,b,c中至少有一个负数
11、若b<0,A=a,B=a+(b),
C=a+b中,比较A、B、C的大小,请你用
“>”
将A、B、C连接起来,其中正确是(
)
A.A>B>C
B.
B>A>C
C.C>B>A
D.
B>C>A
12、下列运算中正确的个数有( )
①(–5)–(–5)=0;②–10–(–7)=–17;③0+(–4)=–4;④?
A.1个
B.2个
C.3个
D.4个
13、自然数的前100个奇数之和减去前100个偶数之和,差为(
)
A.100
B.–100
C.0
D.
200
14、某潜水艇追逐一目标,先潜入水下90米,再下潜30米,然后又上升40米,这艘潜水艇现在
水下80米
处.
15、定义一种新运算=–a+b+c
–d,则的运算结果是
–2.6
.
16、已知a=–3,b=–5,c=12,求下列各式的值:
(1)a–b+c;
(2)a–b–c;
(3)a–(b–c).
7、先阅读下列材料,再解决问题:
如图1是四宫数独的元素示意图.单元格:数独盘面中最小的单位,即一个格子,通常简称为“格”,每个格内只有一个确定的数字.行:数独盘面中水平方向4个单元格组成的区域总称,从上到下依次为A行、B行、C行和D行,用英文字母表示.列:数独盘面中垂直方向4个单元格组成的区域总称,从左到右依次为第1列、第2列、第3列和第4列,用数字表示.宫:数独盘面中围成的2×2单元格组成的区域总称,从上到下、从左到右依次为第一宫、第二宫、第三宫和第四宫.已知数:数独题目中给定的数.
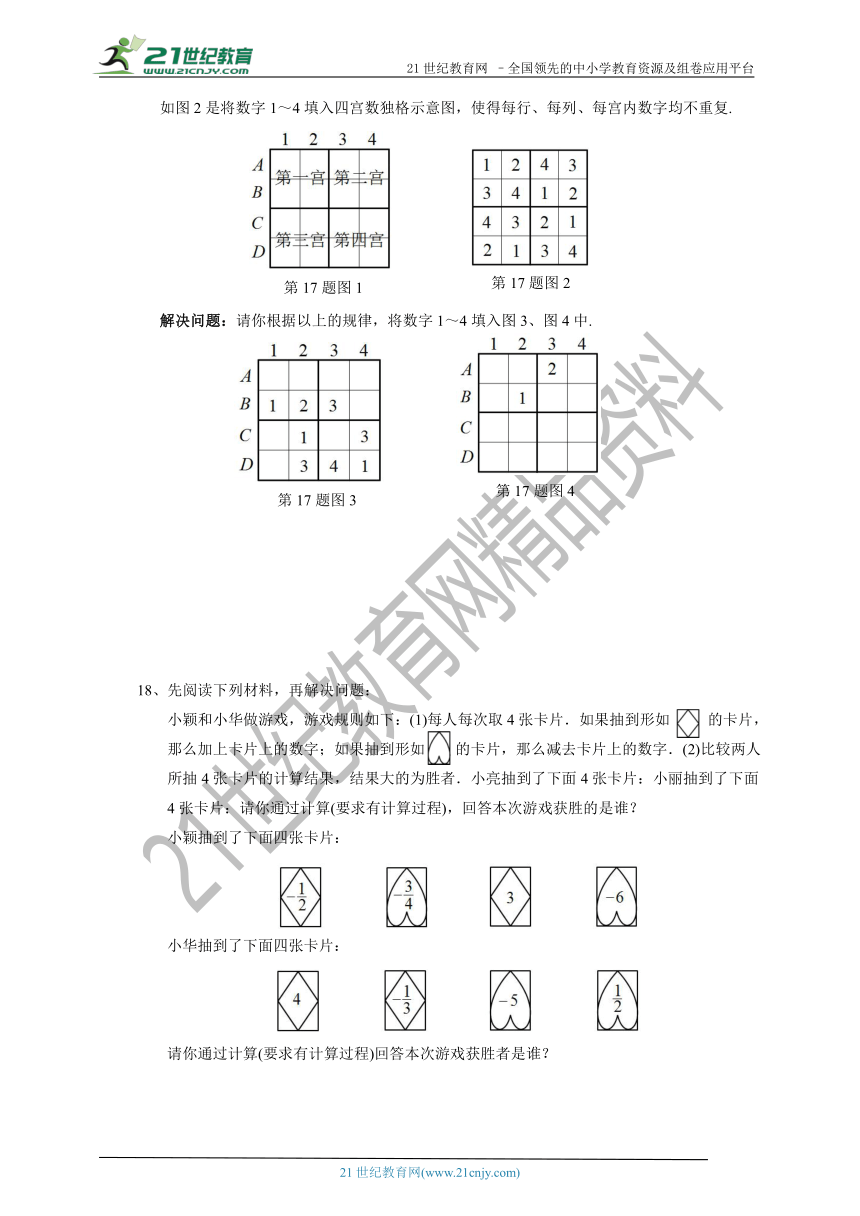
如图2是将数字1~4填入四宫数独格示意图,使得每行、每列、每宫内数字均不重复.
解决问题:请你根据以上的规律,将数字1~4填入图3、图4中.
18、先阅读下列材料,再解决问题:
小颖和小华做游戏,游戏规则如下:(1)每人每次取4张卡片.如果抽到形如
的卡片,那么加上卡片上的数字;如果抽到形如
的卡片,那么减去卡片上的数字.(2)比较两人所抽4张卡片的计算结果,结果大的为胜者.小亮抽到了下面4张卡片:小丽抽到了下面4张卡片:请你通过计算(要求有计算过程),回答本次游戏获胜的是谁?
小颖抽到了下面四张卡片:
小华抽到了下面四张卡片:
请你通过计算(要求有计算过程)回答本次游戏获胜者是谁?
【中考链接】
19、(2020?枣庄)计算的结果为(
)
A.?
B.?
C.
D.
20、(2021?模拟)
把1,–2,3,–4,5,–6,7,–8,9这九个数分别填入下列3×3的网格
中使每行,每列和对角线的三个数字的和都是正数,其中正确的是(
)
参考答案
1、C
2、B
3、B
4、D
5、–1或–5
6、34
7、(1)57,96;(2)26,37;(3)14,11;(4)63
10、D
11、B
12、C
13、A
14、水下80米
15、–2.6
19、A
20、A
8、计算:
(1)
18+22+
(26)(8);
(2)
21(15)(+25)11;
(3)
;
(4).
解:(1)原式=–18+22+
(26)+(+8)
=
[(–18)+(–26)]+
[(+22)+(+8)]
=(–44)+(+30)=–14;
(2)原式=21+(+15)+(–25)+(11)
=36+(–36)=0;
(3)原式=
==0;
(4)原式=
=
=
=.
9、把–1,–2,–3,–4,–5,–6,–7,–8,–9,分别填在下面的方格中,使每一横行,每一竖行和每一斜行上的数相加都得–15.
16、已知a=–3,b=–5,c=12,求下列各式的值:
(1)a–b+c;
(2)a–b–c;
(3)a–(b–c).
解:
(1)a–b+c=–3–(–5)+12
=(–3)+(+5)+12=17;
(2)a–b–c=–3–(–5)–(+
12)
=(–3)+(+5)+(–12)=–10;
(3)a–(b–c)=–3–
[(–5)–12]
=(–3)–
[(–5)+(–12)]
=(–3)–(–17)
=(–3)+(+17)=14.
17、先阅读下列材料,再解决问题:
如图1是四宫数独的元素示意图.单元格:数独盘面中最小的单位,即一个格子,通常简称为“格”,每个格内只有一个确定的数字.行:数独盘面中水平方向4个单元格组成的区域总称,从上到下依次为A行、B行、C行和D行,用英文字母表示.列:数独盘面中垂直方向4个单元格组成的区域总称,从左到右依次为第1列、第2列、第3列和第4列,用数字表示.宫:数独盘面中围成的2×2单元格组成的区域总称,从上到下、从左到右依次为第一宫、第二宫、第三宫和第四宫.已知数:数独题目中给定的数.
如图2是将数字1~4填入四宫数独格示意图,使得每行、每列、每宫内数字均不重复.
解决问题:请你根据以上的规律,将数字1~4填入图3、图4中.
18、先阅读下列材料,再解决问题:
小颖和小华做游戏,游戏规则如下:(1)每人每次取4张卡片.如果抽到形如
的卡片,那么加上卡片上的数字;如果抽到形如
的卡片,那么减去卡片上的数字.(2)比较两人所抽4张卡片的计算结果,结果大的为胜者.小亮抽到了下面4张卡片:小丽抽到了下面4张卡片:请你通过计算(要求有计算过程),回答本次游戏获胜的是谁?
小颖抽到了下面四张卡片:
小华抽到了下面四张卡片:
请你通过计算(要求有计算过程)回答本次游戏获胜者是谁?
解:小颖抽到了下面四张卡片列式为:
=
=9;
小华抽到了下面四张卡片:
=
==.
∵9>,
∴小颖获胜.
第17题图4
第17题图3
第17题图3
第17题图4
第17题图1
第9题图
第17题图3
第17题图2
第9题图
第17题图4
第17题图1
第17题图2
A
B
C
D
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
–全国领先的中小学教育资源及组卷应用平台
北师大版2021–2022学年度七年级数学上册第二章有理数及其运算
2.6
有理数的加减混合运算
第一课时
有理数的加减混合运算(1)
【知识清单】
一、有理数的加减混合运算:
1、有理数加减混合运算即一个算式中既有加法同时也有减法.
2、有理数的加减法混合运算的一般步骤:①在一个算式中,若有减法,应由有理数的减法法则转化为加法;②利用加法则,加法交换律、结合律简化计算.
二、有理数减法运算时注意两“变”:
①改变运算符号;②改变减数的性质符号(变为相反数)
【经典例题】
例题1、计算:
(–2.5)–
()+
【考点】有理数的加减混合运算.
【分析】在一个加减混合运算的算式中,有加法也有减法,应该根据有理数的减法法则把减法转化为加法,然后再按有理数加法法则进行运算.
【解答】(1)原式=
()+
()+(+)
=(–2)+(+3)+(+4)+()+
()+(+)
=5+=.
【点评】该题考查了学生加减混合运算的能力,在一个加减混合运算的算式中,,有理数减法运算的两变一算:(1)一变:把减号边变为加号;(2)二变:变减数为减数的相反数(分清运算符号和性质符号);(3)三算:运用有理数加法的法则进行计算,求出结果.
例题2、数学活动课上,王老师给同学们出了一道题:规定一种新运算“☆”,对于任意有理数a和b,有a☆b=
b–a+5,根据新运算,计算(–3☆2)☆(–4)的值是
.
【考点】有理数的混合运算.?
【分析】根据题中给出的a☆b=
b–a+5列出代数式,进行计算即可.
【解答】原式=[2–
(–3)+5]☆(–4)
=10☆(–4)
=–4–
(+10)+5
=–9.
答案为:9.
【点评】本题考查的是有理数的混合运算,熟知有理数混合运算的法则和正确套入新运算“☆”是解答此题的关键.
【夯实基础】
1、某天海口温度是零上31℃,而黑龙江漠河的温度是零下29℃,海口比漠河温度高出(
)
A.–2℃
B.2℃
C.60℃
D.–60℃
2、计算的值为(
)
A.
B.
C.
D.
3、某运动员在东西走向的公路上练习跑步,跑步情况记录如下(向东为正,单位:米):1000,–1200,
1100,–800,1400,该运动员跑的路程共为( )
A.1500米
B.5500米
C.4500米
D.3700米
4、计算(–4)–(+2)+
(–6)–(–4)的结果是(
)
A.
–4
B.–12
C.–10
D.–8
5、已知|a|=2,|b|=4,|c|=7,且a>b>c,则a–b+c=
.
6、–12,+8,–5的和比它们绝对值的和小
.
7、找规律填数:
(1)
3,4,7,11,18,39,
,
;
(2)
2,5,10,17,
,
;
(3)
6,3,8,5,10,7,12,9,
,
;
(4)
1,3,7,15,31,
,127,225.
8、计算:
(1)18+22+
(26)(8);
(2)
21(15)(+25)11;
(3)
;
(4).
9、把–1,–2,–3,–4,–5,–6,–7,–8,–9,分别填在下面的方格中,使每一横行,每一竖行和每一斜行上的数相加都得–15.
【提优特训】
10、若a+b+c=0,则下列结论正确的是
A.a=b=c=0
B.a,b,c中至少有两个负数
C.a,b,c中至少有两个互为相反数
D.a,b,c中至少有一个负数
11、若b<0,A=a,B=a+(b),
C=a+b中,比较A、B、C的大小,请你用
“>”
将A、B、C连接起来,其中正确是(
)
A.A>B>C
B.
B>A>C
C.C>B>A
D.
B>C>A
12、下列运算中正确的个数有( )
①(–5)–(–5)=0;②–10–(–7)=–17;③0+(–4)=–4;④?
A.1个
B.2个
C.3个
D.4个
13、自然数的前100个奇数之和减去前100个偶数之和,差为(
)
A.100
B.–100
C.0
D.
200
14、某潜水艇追逐一目标,先潜入水下90米,再下潜30米,然后又上升40米,这艘潜水艇现在
水下80米
处.
15、定义一种新运算=–a+b+c
–d,则的运算结果是
–2.6
.
16、已知a=–3,b=–5,c=12,求下列各式的值:
(1)a–b+c;
(2)a–b–c;
(3)a–(b–c).
7、先阅读下列材料,再解决问题:
如图1是四宫数独的元素示意图.单元格:数独盘面中最小的单位,即一个格子,通常简称为“格”,每个格内只有一个确定的数字.行:数独盘面中水平方向4个单元格组成的区域总称,从上到下依次为A行、B行、C行和D行,用英文字母表示.列:数独盘面中垂直方向4个单元格组成的区域总称,从左到右依次为第1列、第2列、第3列和第4列,用数字表示.宫:数独盘面中围成的2×2单元格组成的区域总称,从上到下、从左到右依次为第一宫、第二宫、第三宫和第四宫.已知数:数独题目中给定的数.
如图2是将数字1~4填入四宫数独格示意图,使得每行、每列、每宫内数字均不重复.
解决问题:请你根据以上的规律,将数字1~4填入图3、图4中.
18、先阅读下列材料,再解决问题:
小颖和小华做游戏,游戏规则如下:(1)每人每次取4张卡片.如果抽到形如
的卡片,那么加上卡片上的数字;如果抽到形如
的卡片,那么减去卡片上的数字.(2)比较两人所抽4张卡片的计算结果,结果大的为胜者.小亮抽到了下面4张卡片:小丽抽到了下面4张卡片:请你通过计算(要求有计算过程),回答本次游戏获胜的是谁?
小颖抽到了下面四张卡片:
小华抽到了下面四张卡片:
请你通过计算(要求有计算过程)回答本次游戏获胜者是谁?
【中考链接】
19、(2020?枣庄)计算的结果为(
)
A.?
B.?
C.
D.
20、(2021?模拟)
把1,–2,3,–4,5,–6,7,–8,9这九个数分别填入下列3×3的网格
中使每行,每列和对角线的三个数字的和都是正数,其中正确的是(
)
参考答案
1、C
2、B
3、B
4、D
5、–1或–5
6、34
7、(1)57,96;(2)26,37;(3)14,11;(4)63
10、D
11、B
12、C
13、A
14、水下80米
15、–2.6
19、A
20、A
8、计算:
(1)
18+22+
(26)(8);
(2)
21(15)(+25)11;
(3)
;
(4).
解:(1)原式=–18+22+
(26)+(+8)
=
[(–18)+(–26)]+
[(+22)+(+8)]
=(–44)+(+30)=–14;
(2)原式=21+(+15)+(–25)+(11)
=36+(–36)=0;
(3)原式=
==0;
(4)原式=
=
=
=.
9、把–1,–2,–3,–4,–5,–6,–7,–8,–9,分别填在下面的方格中,使每一横行,每一竖行和每一斜行上的数相加都得–15.
16、已知a=–3,b=–5,c=12,求下列各式的值:
(1)a–b+c;
(2)a–b–c;
(3)a–(b–c).
解:
(1)a–b+c=–3–(–5)+12
=(–3)+(+5)+12=17;
(2)a–b–c=–3–(–5)–(+
12)
=(–3)+(+5)+(–12)=–10;
(3)a–(b–c)=–3–
[(–5)–12]
=(–3)–
[(–5)+(–12)]
=(–3)–(–17)
=(–3)+(+17)=14.
17、先阅读下列材料,再解决问题:
如图1是四宫数独的元素示意图.单元格:数独盘面中最小的单位,即一个格子,通常简称为“格”,每个格内只有一个确定的数字.行:数独盘面中水平方向4个单元格组成的区域总称,从上到下依次为A行、B行、C行和D行,用英文字母表示.列:数独盘面中垂直方向4个单元格组成的区域总称,从左到右依次为第1列、第2列、第3列和第4列,用数字表示.宫:数独盘面中围成的2×2单元格组成的区域总称,从上到下、从左到右依次为第一宫、第二宫、第三宫和第四宫.已知数:数独题目中给定的数.
如图2是将数字1~4填入四宫数独格示意图,使得每行、每列、每宫内数字均不重复.
解决问题:请你根据以上的规律,将数字1~4填入图3、图4中.
18、先阅读下列材料,再解决问题:
小颖和小华做游戏,游戏规则如下:(1)每人每次取4张卡片.如果抽到形如
的卡片,那么加上卡片上的数字;如果抽到形如
的卡片,那么减去卡片上的数字.(2)比较两人所抽4张卡片的计算结果,结果大的为胜者.小亮抽到了下面4张卡片:小丽抽到了下面4张卡片:请你通过计算(要求有计算过程),回答本次游戏获胜的是谁?
小颖抽到了下面四张卡片:
小华抽到了下面四张卡片:
请你通过计算(要求有计算过程)回答本次游戏获胜者是谁?
解:小颖抽到了下面四张卡片列式为:
=
=9;
小华抽到了下面四张卡片:
=
==.
∵9>,
∴小颖获胜.
第17题图4
第17题图3
第17题图3
第17题图4
第17题图1
第9题图
第17题图3
第17题图2
第9题图
第17题图4
第17题图1
第17题图2
A
B
C
D
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
