专题强化训练2 平面向量-北师大版高中数学必修四练习(Word含解析)
文档属性
| 名称 | 专题强化训练2 平面向量-北师大版高中数学必修四练习(Word含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 238.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-16 00:17:30 | ||
图片预览



文档简介
专题强化训练(二) 平面向量
(建议用时:40分钟)
一、选择题
1.下列命题中正确的是( )
A.-= B.+=0
C.0·=0 D.++=
2.已知点A(-1,-2)按向量a平移后变为A′(0,1),点B(2,-1)按向量a平移后对应点B′的坐标为( )
A.(3,1) B.(1,3)
C.(3,2) D.(2,3)
3.已知向量a,b满足|a|=1,a·b=-1,则a·(2a-b)=( )
A.4 B.3 C.2 D.0
4.已知O为平面上的一个定点,A,B,C是该平面上不共线的三点,若(-)·(+-2)=0,则△ABC是( )
A.以AB为底边的等腰三角形
B.以BC为底边的等腰三角形
C.以AB为斜边的直角三角形
D.以BC为斜边的直角三角形
5.对任意向量a,b,下列关系式中不恒成立的是( )
A.|a·b|≤|a||b|
B.|a-b|≤||a|-|b||
C.(a+b)2=|a+b|2
D.(a+b)·(a-b)=a2-b2
二、填空题
6.已知a与b为两个不共线的单位向量,k为实数,若向量a+b与向量ka-b垂直,则k=________.
7.已知向量a=(,1),b=(0,-1),c=(k,),若a-2b与c共线,则k=________.
8.给出下列结论:
①若a≠0,a·b=0,则b=0;②若a·b=b·c,则a=c;③(a·b)c=a(b·c);④a·[b(a·c)-c(a·b)]=0.其中正确结论的序号是________.
三、解答题
9.已知|a|=,|b|=1.
(1)若a,b的夹角θ为45°,求|a-b|;
(2)若(a-b)⊥b,求a与b的夹角θ.
10.已知=(2,1),=(1,7),=(5,1),设C是直线OP上的一点(其中O为坐标原点).
(1)求使·取得最小值时的;
(2)对(1)中求出的点C,求cos ∠ACB.
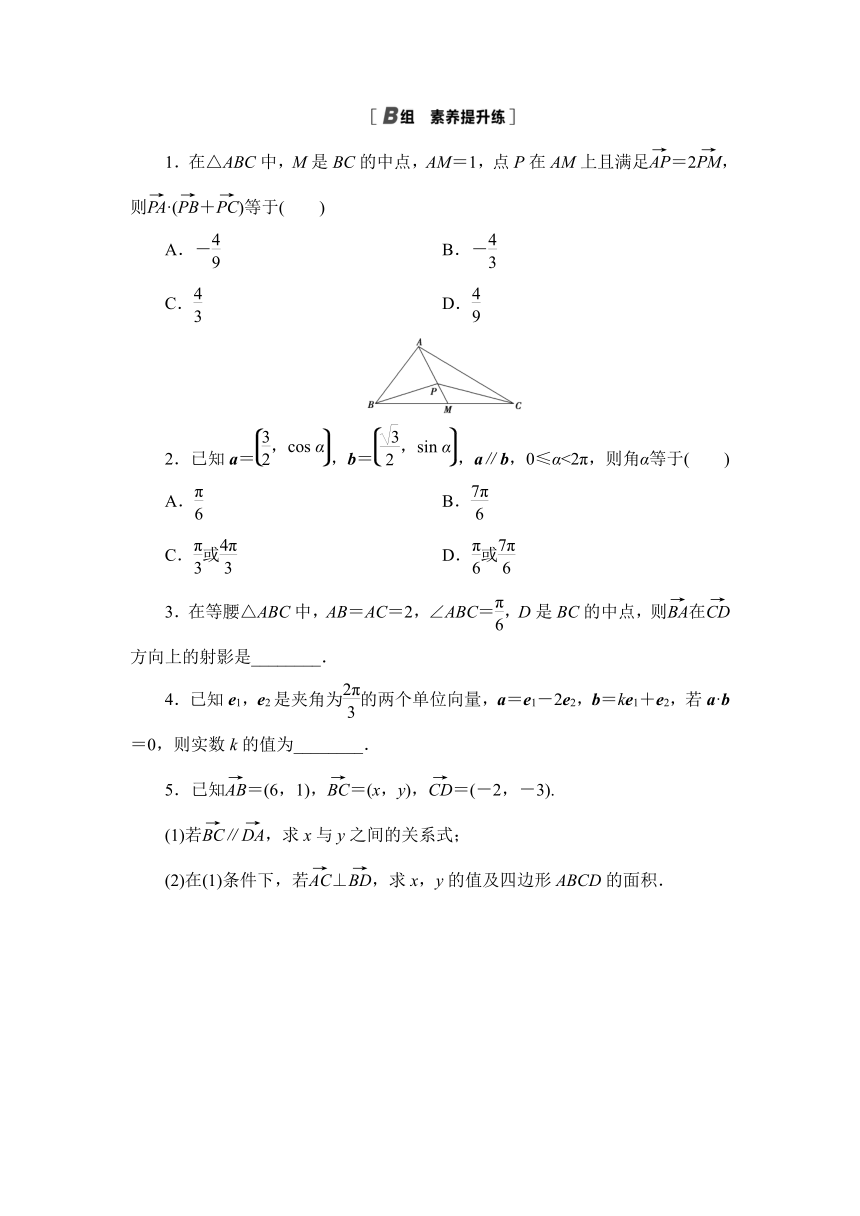
1.在△ABC中,M是BC的中点,AM=1,点P在AM上且满足=2,则·(+)等于( )
A.- B.-
C. D.
2.已知a=,b=,a∥b,0≤α<2π,则角α等于( )
A. B.
C.或 D.或
3.在等腰△ABC中,AB=AC=2,∠ABC=,D是BC的中点,则在方向上的射影是________.
4.已知e1,e2是夹角为的两个单位向量,a=e1-2e2,b=ke1+e2,若a·b=0,则实数k的值为________.
5.已知=(6,1),=(x,y),=(-2,-3).
(1)若∥,求x与y之间的关系式;
(2)在(1)条件下,若⊥,求x,y的值及四边形ABCD的面积.
专题强化训练(二) 平面向量
(建议用时:40分钟)
一、选择题
1.下列命题中正确的是( )
A.-= B.+=0
C.0·=0 D.++=
D [起点相同的向量相减,则取终点,并指向被减向量,-=;,是一对相反向量,它们的和应该为零向量,+=0;0·=0.]
2.已知点A(-1,-2)按向量a平移后变为A′(0,1),点B(2,-1)按向量a平移后对应点B′的坐标为( )
A.(3,1) B.(1,3)
C.(3,2) D.(2,3)
C [设a=(x,y),则有-1+x=0,-2+y=1,所以a=(1,3).点B(2,-1)按向量a平移后对应点B′的坐标为(3,2).]
3.已知向量a,b满足|a|=1,a·b=-1,则a·(2a-b)=( )
A.4 B.3 C.2 D.0
B [a·(2a-b)=2a2-a·b=2|a|2-a·b.
∵|a|=1,a·b=-1,∴原式=2×12+1=3.
故选B.]
4.已知O为平面上的一个定点,A,B,C是该平面上不共线的三点,若(-)·(+-2)=0,则△ABC是( )
A.以AB为底边的等腰三角形
B.以BC为底边的等腰三角形
C.以AB为斜边的直角三角形
D.以BC为斜边的直角三角形
B [由题意知(-)·(+-2)=·(+)=0,如图所示,其中+=2(点D为线段BC的中点),所以AD⊥BC,即AD是BC的中垂线,所以AB=AC,即△ABC为等腰三角形.故选B.]
5.对任意向量a,b,下列关系式中不恒成立的是( )
A.|a·b|≤|a||b|
B.|a-b|≤||a|-|b||
C.(a+b)2=|a+b|2
D.(a+b)·(a-b)=a2-b2
B [根据a·b=|a||b|cos θ,又cos θ≤1,知|a·b|≤|a||b|,A恒成立.当向量a和b方向不相同时,|a-b|>||a|-|b||,B不恒成立.根据|a+b|2=a2+2a·b+b2=(a+b)2,C恒成立.根据向量的运算性质得(a+b)·(a-b)=a2-b2,D恒成立.]
二、填空题
6.已知a与b为两个不共线的单位向量,k为实数,若向量a+b与向量ka-b垂直,则k=________.
1 [(a+b)·(ka-b)=(k-1)(1+a·b),由于|a|=1,|b|=1,且a与b不共线,∴1+a·b≠0.又(k-1)·(1+a·b)=0.∴k=1.]
7.已知向量a=(,1),b=(0,-1),c=(k,),若a-2b与c共线,则k=________.
1 [a-2b=(,3),
∵(a-2b)∥c,
∴3-3k=0,∴k=1.]
8.给出下列结论:
①若a≠0,a·b=0,则b=0;②若a·b=b·c,则a=c;③(a·b)c=a(b·c);④a·[b(a·c)-c(a·b)]=0.其中正确结论的序号是________.
④ [因为两个非零向量a、b垂直时,a·b=0,故①不正确;
当a=0,b⊥c时,a·b=b·c=0,但不能得出a=c,故②不正确;
向量(a·b)c与c共线,a(b·c)与a共线,故③不正确;
a·[b(a·c)-c(a·b)]=(a·b)(a·c)-(a·c)(a·b)=0,故④正确.]
三、解答题
9.已知|a|=,|b|=1.
(1)若a,b的夹角θ为45°,求|a-b|;
(2)若(a-b)⊥b,求a与b的夹角θ.
[解] (1)|a-b|=
= =1.
(2)∵(a-b)⊥b,
∴(a-b)·b=a·b-b2=×1×cos θ-1=0,
∴cos θ=,又∵0≤θ≤π,∴θ=.
10.已知=(2,1),=(1,7),=(5,1),设C是直线OP上的一点(其中O为坐标原点).
(1)求使·取得最小值时的;
(2)对(1)中求出的点C,求cos ∠ACB.
[解] (1)∵点C是直线OP上的一点,
∴向量与共线,
设=t(t∈R),则=t(2,1)=(2t,t),
∴=-=(1-2t,7-t),
=-=(5-2t,1-t),
∴·=(1-2t)(5-2t)+(7-t)(1-t)
=5t2-20t+12=5(t-2)2-8.
∴当t=2时,·取得最小值,此时=(4,2).
(2)由(1)知=(4,2),∴=(-3,5),=(1,-1),
∴||=,||=,·=-3-5=-8.
∴cos ∠ACB==-.
1.在△ABC中,M是BC的中点,AM=1,点P在AM上且满足=2,则·(+)等于( )
A.- B.-
C. D.
A [·(+)
=·2=2||·||·cos 180°
=2×××(-1)=-.]
2.已知a=,b=,a∥b,0≤α<2π,则角α等于( )
A. B.
C.或 D.或
D [因为a∥b,所以sin α=cos α,
所以tan α=,又0≤α<2π,所以α=或.]
3.在等腰△ABC中,AB=AC=2,∠ABC=,D是BC的中点,则在方向上的射影是________.
- [由题意知,与所成的角为,
∴在方向上的射影是2×cos =-.]
4.已知e1,e2是夹角为的两个单位向量,a=e1-2e2,b=ke1+e2,若a·b=0,则实数k的值为________.
[由题意得:a·b=(e1-2e2)·(ke1+e2)=0,
即ke+e1·e2-2ke1·e2-2e=0,则k+cos -2k cos -2=0,化简得k=.]
5.已知=(6,1),=(x,y),=(-2,-3).
(1)若∥,求x与y之间的关系式;
(2)在(1)条件下,若⊥,求x,y的值及四边形ABCD的面积.
[解] (1)∵=++=(x+4,y-2),
∴=-=(-x-4,2-y).
又∵∥且=(x,y),
∴x(2-y)-y(-x-4)=0,
即x+2y=0. ①
(2)由于=+=(x+6,y+1),
=+=(x-2,y-3),
又⊥,
所以·=0,
即(x+6)(x-2)+(y+1)(y-3)=0. ②
联立①②化简,得y2-2y-3=0.
解得y=3或y=-1.
故当y=3时,x=-6,
此时=(0,4),=(-8,0),
所以SABCD=||·||=16;
当y=-1时,x=2,
此时=(8,0),=(0,-4),
∴SABCD=||·||=16.
(建议用时:40分钟)
一、选择题
1.下列命题中正确的是( )
A.-= B.+=0
C.0·=0 D.++=
2.已知点A(-1,-2)按向量a平移后变为A′(0,1),点B(2,-1)按向量a平移后对应点B′的坐标为( )
A.(3,1) B.(1,3)
C.(3,2) D.(2,3)
3.已知向量a,b满足|a|=1,a·b=-1,则a·(2a-b)=( )
A.4 B.3 C.2 D.0
4.已知O为平面上的一个定点,A,B,C是该平面上不共线的三点,若(-)·(+-2)=0,则△ABC是( )
A.以AB为底边的等腰三角形
B.以BC为底边的等腰三角形
C.以AB为斜边的直角三角形
D.以BC为斜边的直角三角形
5.对任意向量a,b,下列关系式中不恒成立的是( )
A.|a·b|≤|a||b|
B.|a-b|≤||a|-|b||
C.(a+b)2=|a+b|2
D.(a+b)·(a-b)=a2-b2
二、填空题
6.已知a与b为两个不共线的单位向量,k为实数,若向量a+b与向量ka-b垂直,则k=________.
7.已知向量a=(,1),b=(0,-1),c=(k,),若a-2b与c共线,则k=________.
8.给出下列结论:
①若a≠0,a·b=0,则b=0;②若a·b=b·c,则a=c;③(a·b)c=a(b·c);④a·[b(a·c)-c(a·b)]=0.其中正确结论的序号是________.
三、解答题
9.已知|a|=,|b|=1.
(1)若a,b的夹角θ为45°,求|a-b|;
(2)若(a-b)⊥b,求a与b的夹角θ.
10.已知=(2,1),=(1,7),=(5,1),设C是直线OP上的一点(其中O为坐标原点).
(1)求使·取得最小值时的;
(2)对(1)中求出的点C,求cos ∠ACB.
1.在△ABC中,M是BC的中点,AM=1,点P在AM上且满足=2,则·(+)等于( )
A.- B.-
C. D.
2.已知a=,b=,a∥b,0≤α<2π,则角α等于( )
A. B.
C.或 D.或
3.在等腰△ABC中,AB=AC=2,∠ABC=,D是BC的中点,则在方向上的射影是________.
4.已知e1,e2是夹角为的两个单位向量,a=e1-2e2,b=ke1+e2,若a·b=0,则实数k的值为________.
5.已知=(6,1),=(x,y),=(-2,-3).
(1)若∥,求x与y之间的关系式;
(2)在(1)条件下,若⊥,求x,y的值及四边形ABCD的面积.
专题强化训练(二) 平面向量
(建议用时:40分钟)
一、选择题
1.下列命题中正确的是( )
A.-= B.+=0
C.0·=0 D.++=
D [起点相同的向量相减,则取终点,并指向被减向量,-=;,是一对相反向量,它们的和应该为零向量,+=0;0·=0.]
2.已知点A(-1,-2)按向量a平移后变为A′(0,1),点B(2,-1)按向量a平移后对应点B′的坐标为( )
A.(3,1) B.(1,3)
C.(3,2) D.(2,3)
C [设a=(x,y),则有-1+x=0,-2+y=1,所以a=(1,3).点B(2,-1)按向量a平移后对应点B′的坐标为(3,2).]
3.已知向量a,b满足|a|=1,a·b=-1,则a·(2a-b)=( )
A.4 B.3 C.2 D.0
B [a·(2a-b)=2a2-a·b=2|a|2-a·b.
∵|a|=1,a·b=-1,∴原式=2×12+1=3.
故选B.]
4.已知O为平面上的一个定点,A,B,C是该平面上不共线的三点,若(-)·(+-2)=0,则△ABC是( )
A.以AB为底边的等腰三角形
B.以BC为底边的等腰三角形
C.以AB为斜边的直角三角形
D.以BC为斜边的直角三角形
B [由题意知(-)·(+-2)=·(+)=0,如图所示,其中+=2(点D为线段BC的中点),所以AD⊥BC,即AD是BC的中垂线,所以AB=AC,即△ABC为等腰三角形.故选B.]
5.对任意向量a,b,下列关系式中不恒成立的是( )
A.|a·b|≤|a||b|
B.|a-b|≤||a|-|b||
C.(a+b)2=|a+b|2
D.(a+b)·(a-b)=a2-b2
B [根据a·b=|a||b|cos θ,又cos θ≤1,知|a·b|≤|a||b|,A恒成立.当向量a和b方向不相同时,|a-b|>||a|-|b||,B不恒成立.根据|a+b|2=a2+2a·b+b2=(a+b)2,C恒成立.根据向量的运算性质得(a+b)·(a-b)=a2-b2,D恒成立.]
二、填空题
6.已知a与b为两个不共线的单位向量,k为实数,若向量a+b与向量ka-b垂直,则k=________.
1 [(a+b)·(ka-b)=(k-1)(1+a·b),由于|a|=1,|b|=1,且a与b不共线,∴1+a·b≠0.又(k-1)·(1+a·b)=0.∴k=1.]
7.已知向量a=(,1),b=(0,-1),c=(k,),若a-2b与c共线,则k=________.
1 [a-2b=(,3),
∵(a-2b)∥c,
∴3-3k=0,∴k=1.]
8.给出下列结论:
①若a≠0,a·b=0,则b=0;②若a·b=b·c,则a=c;③(a·b)c=a(b·c);④a·[b(a·c)-c(a·b)]=0.其中正确结论的序号是________.
④ [因为两个非零向量a、b垂直时,a·b=0,故①不正确;
当a=0,b⊥c时,a·b=b·c=0,但不能得出a=c,故②不正确;
向量(a·b)c与c共线,a(b·c)与a共线,故③不正确;
a·[b(a·c)-c(a·b)]=(a·b)(a·c)-(a·c)(a·b)=0,故④正确.]
三、解答题
9.已知|a|=,|b|=1.
(1)若a,b的夹角θ为45°,求|a-b|;
(2)若(a-b)⊥b,求a与b的夹角θ.
[解] (1)|a-b|=
= =1.
(2)∵(a-b)⊥b,
∴(a-b)·b=a·b-b2=×1×cos θ-1=0,
∴cos θ=,又∵0≤θ≤π,∴θ=.
10.已知=(2,1),=(1,7),=(5,1),设C是直线OP上的一点(其中O为坐标原点).
(1)求使·取得最小值时的;
(2)对(1)中求出的点C,求cos ∠ACB.
[解] (1)∵点C是直线OP上的一点,
∴向量与共线,
设=t(t∈R),则=t(2,1)=(2t,t),
∴=-=(1-2t,7-t),
=-=(5-2t,1-t),
∴·=(1-2t)(5-2t)+(7-t)(1-t)
=5t2-20t+12=5(t-2)2-8.
∴当t=2时,·取得最小值,此时=(4,2).
(2)由(1)知=(4,2),∴=(-3,5),=(1,-1),
∴||=,||=,·=-3-5=-8.
∴cos ∠ACB==-.
1.在△ABC中,M是BC的中点,AM=1,点P在AM上且满足=2,则·(+)等于( )
A.- B.-
C. D.
A [·(+)
=·2=2||·||·cos 180°
=2×××(-1)=-.]
2.已知a=,b=,a∥b,0≤α<2π,则角α等于( )
A. B.
C.或 D.或
D [因为a∥b,所以sin α=cos α,
所以tan α=,又0≤α<2π,所以α=或.]
3.在等腰△ABC中,AB=AC=2,∠ABC=,D是BC的中点,则在方向上的射影是________.
- [由题意知,与所成的角为,
∴在方向上的射影是2×cos =-.]
4.已知e1,e2是夹角为的两个单位向量,a=e1-2e2,b=ke1+e2,若a·b=0,则实数k的值为________.
[由题意得:a·b=(e1-2e2)·(ke1+e2)=0,
即ke+e1·e2-2ke1·e2-2e=0,则k+cos -2k cos -2=0,化简得k=.]
5.已知=(6,1),=(x,y),=(-2,-3).
(1)若∥,求x与y之间的关系式;
(2)在(1)条件下,若⊥,求x,y的值及四边形ABCD的面积.
[解] (1)∵=++=(x+4,y-2),
∴=-=(-x-4,2-y).
又∵∥且=(x,y),
∴x(2-y)-y(-x-4)=0,
即x+2y=0. ①
(2)由于=+=(x+6,y+1),
=+=(x-2,y-3),
又⊥,
所以·=0,
即(x+6)(x-2)+(y+1)(y-3)=0. ②
联立①②化简,得y2-2y-3=0.
解得y=3或y=-1.
故当y=3时,x=-6,
此时=(0,4),=(-8,0),
所以SABCD=||·||=16;
当y=-1时,x=2,
此时=(8,0),=(0,-4),
∴SABCD=||·||=16.
