2021年春黑龙江省八年级数学第一次月考试题(word版含答案)
文档属性
| 名称 | 2021年春黑龙江省八年级数学第一次月考试题(word版含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 302.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-16 00:00:00 | ||
图片预览



文档简介
2021年春黑龙江省八年级数学第一次月考试题
(考试总分:120
分)
一、
单选题
(本题共计10小题,总分30分)
1.(3分)1.在下列四个标志中,既是中心对称又是轴对称图形的是( )
A.
B.
C.
D.
2.(3分)2.不等式2x>3-x的解集是(
)
A.x>3
B.x<3
C.x>1
D.x<1
3.(3分)3.一次函数y=kx+b(k,b是常数,k≠0)的图象如图所示,则不等式kx+b>0的解集是( )
A.x>0
B.x>3
C.x<0
D.x<3
4.(3分)4.不等式组的整数解共有( )
A.1个
B.2个
C.3个
D.4个
5.(3分)5.为有效开展“阳光体育”活动,某校计划购买篮球和足球共50个,购买资金不超过3000元.若每个篮球80元,每个足球50元,则篮球最多可购买(
)
A.16个
B.17个
C.33个
D.34个
6.(3分)6.若一次函数的图象经过点和,则不等式的解集为(
)
A.
B.
C.
D.
7.(3分)7.如果不等式的解集是,则a的取值范围是(
)
A.
B.
C.
D.
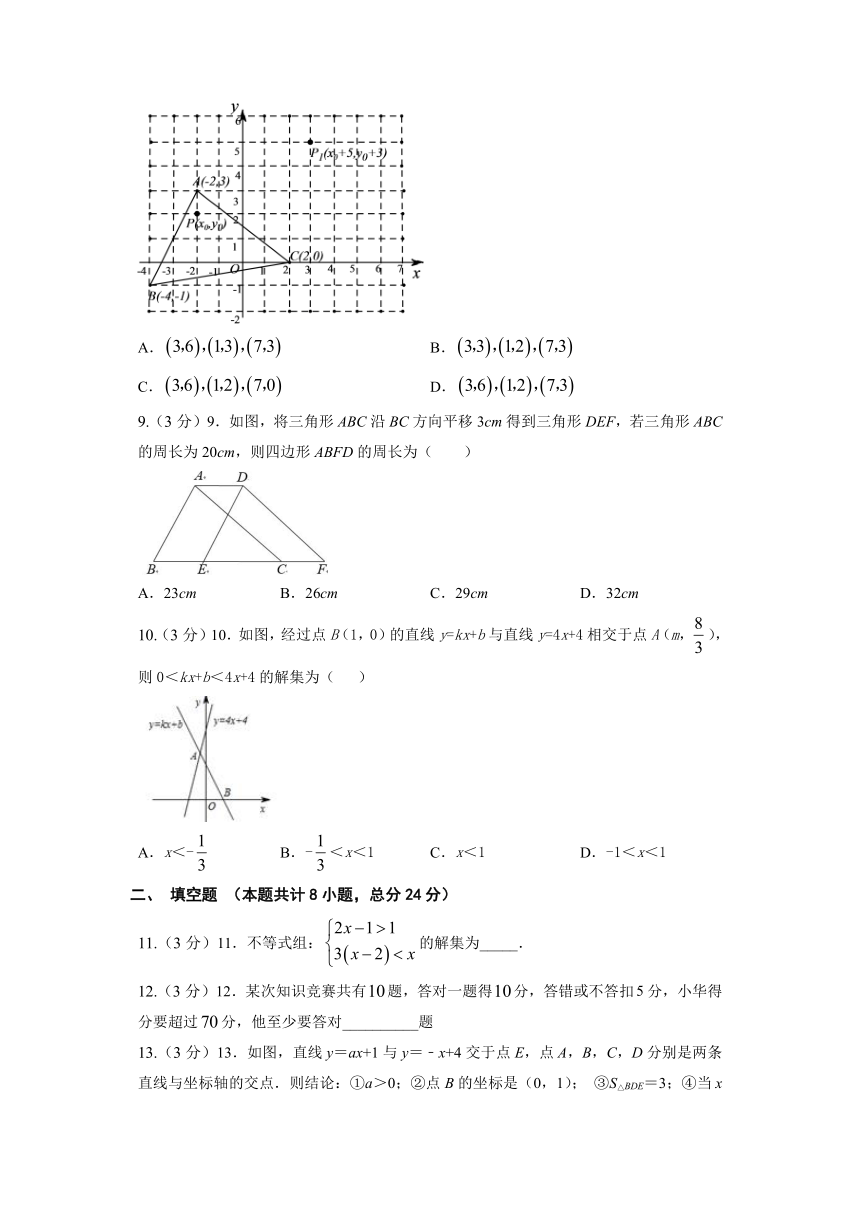
8.(3分)8.如图,中任意一点经平移后对应点为,将作同样的平移得到.则的坐标分别是(
)
A.
B.
C.
D.
9.(3分)9.如图,将三角形ABC沿BC方向平移3cm得到三角形DEF,若三角形ABC的周长为20cm,则四边形ABFD的周长为( )
A.23cm
B.26cm
C.29cm
D.32cm
10.(3分)10.如图,经过点B(1,0)的直线y=kx+b与直线y=4x+4相交于点A(m,),则0<kx+b<4x+4的解集为(
)
A.x<-
B.-<x<1
C.x<1
D.-1<x<1
二、
填空题
(本题共计8小题,总分24分)
11.(3分)11.不等式组:的解集为_____.
12.(3分)12.某次知识竞赛共有题,答对一题得分,答错或不答扣分,小华得分要超过分,他至少要答对__________题
13.(3分)13.如图,直线y=ax+1与y=﹣x+4交于点E,点A,B,C,D分别是两条直线与坐标轴的交点.则结论:①a>0;②点B的坐标是(0,1);
③S△BDE=3;④当x>2时,ax+1<﹣x+4中,正确的有_____.(只填序号)
14.(3分)14.点A(a,3)与点B(﹣4,b)关于原点对称,则a+b=_____.
15.(3分)15.如图,∠C=90°,将直角三角形ABC沿着射线BC方向平移6cm,得三角形A′B′C′,已知BC=3cm,AC=4cm,则阴影部分的面积为_____cm2.
16.(3分)16.如图,一次函数y1=x+b与一次函数y2=kx+4的图象交于点P(1,3),则关于x的不等式x+b>kx+4的解集是_____.
17.(3分)17.若关于的不等式组无解,
则的取值范围是
________.
18.(3分)18.如图,在平面直角坐标系中,将△ABO绕点A顺时针旋转到△AB1C1的位置,点B、O分别落在点B1、C1处,点B1在x轴上,再将△AB1C1绕点B1顺时针旋转到△A1B1C2的位置,点C2在x轴上,将△A1B1C2绕点C2顺时针旋转到△A2B2C2的位置,点A2在x轴上,依次进行下去….若点A(,0),B(0,4),则点B2014的横坐标为______.
三、
解答题
(本题共计7小题,总分66分)
19.(16分)19.解不等式(每题4分,共16分)
(1)
,
(2
)
(3)
(4)
20.(6分)20.()已知方程组,其中x为非正数,y为负数.
(1)求m的取值范围;
(2)不等式2mx+x<2m+1的解集为x>1,求m的整数值.
21.(8分)21.如图,直线y=-2x与直线y=kx+b相交于点A(a,2),并且直线y=kx+b经过x轴上点B(2,0).
(1)求直线y=kx+b的解析式;
(2)求两条直线与y轴围成的三角形面积;
(3)直接写出不等式(k+2)x+b≥0的解集.
22.(8分)22.某教育行政部门计划今年暑假组织部分教师到外地学习,预订宾馆住宿时,有住宿条件一样的甲、乙两家宾馆供选择,两家宾馆房源都很充足,其收费标准均为每人每天元,并且各自推出不同的优惠方案.甲宾馆是人(含人)以内的按标准收费,超过人的,超出部分按九折收费,乙宾馆是人(含人)以内的标准收费,超过人的,超出部分按八折收费.
(1)当人数超过多少人时,选乙宾馆更实惠些?
(2)此行教师人数不到人,选择住乙宾馆比选择住甲宾馆可节省少多元,问此行教师有多少人?
23.(8分)23.如图,方格纸上每个小正方形的边长均为1个单位长度,点A、B都在格点上(两条网格线的交点叫格点).
(1)将线段AB向上平移两个单位长度,点A的对应点为点,点B的对应点为点,请画出平移后的线段;
(2)将线段绕点按逆时针方向旋转,点的对应点为点,请画出旋转后的线段;
(3)连接、,求的面积.
24.(10分)24.某市正在举行文化艺术节活动,一商店抓住商机,决定购进甲,乙两种艺术节纪念品.若购进甲种纪念品4件,乙种纪念品3件,需要550元,若购进甲种纪念品5件,乙种纪念品6件,需要800元.
(1)求购进甲、乙两种纪念品每件各需多少元?
(2)若该商店决定购进这两种纪念品共80件,其中甲种纪念品的数量不少于60件.考虑到资金周转,用于购买这80件纪念品的资金不能超过7100元,那么该商店共有几种进货方案7
(3)若销售每件甲种纪含晶可获利润20元,每件乙种纪念品可获利润30元.在(2)中的各种进货方案中,若全部销售完,哪一种方案获利最大?最大利利润多少元?
25.(10分)25.如图1,在平面直角坐标系中,点A,B的坐标分别为A(a,0),B(b,0),且a,b满足|2a+6|+(2a﹣3b+12)2=0,现同时将点A,B分别向左平移2个单位,再向上平移2个单位,分别得到点A,B的对应点C,D,连接AC,BD.
(1)请直接写出A、B、C、D四点的坐标;
(2)如图2,点P是线段AC上的一个动点,点Q是线段CD的中点,连接PQ,PO,当点P在线段AC上移动时(不与A,C重合),请找出∠PQD,∠OPQ,∠POB的数量关系,并证明你的结论;
(3)在坐标轴上是否存在点M,使三角形MAD的面积与三角形ACD的面积相等?若存在,直接写出点M的坐标;若不存在,试说明理由.
答案
一、
单选题
(本题共计10小题,总分30分)
1.(3分)C
2.(3分)C
3.(3分)D
4.(3分)C
5.(3分)A
6.(3分)A
7.(3分)D
8.(3分)D
9.(3分)B
10.(3分)B
二、
填空题
(本题共计8小题,总分24分)
11.(3分)11.
12.(3分)12.9
13.(3分)13.①②③
14.(3分)14.1.
15.(3分)15.18
16.(3分)16.x>1.
17.(3分)17.
18.(3分)18.10070
三、
解答题
(本题共计7小题,总分66分)
19.(16分)19.x>-6,
;
不等式组的解集是﹣1≤x<2,在数轴上表示不等式组的解集见解析.
,非负整数解为和
20.(6分)20.(1);(2).
21.(8分)21.(1)一次函数的解析式是y=-x+;(2)S△ABC=;(3)x≥-1.
【解析】
试题分析:利用代入法求出点A的坐标,然后根据待定系数法求出一次函数的解析式;
(2)根据图像求出交点C的坐标,然后可求三角形的面积;
(3)根据图像的位置求出不等式的解集.
试题解析:解:(1)把A(a,2)代入y=-2x中,得-2a=2,∴a=-1,∴A(-1,2),把A(-1,2)、B(2,0)代入y=kx+b中得,∴k=-,b=,∴一次函数的解析式是y=-x+;
(2)设直线AB与y轴交于点C,则C(0,),∴S△ABC=××1=;
(3)不等式(k+2)x+b≥0可以变形为kx+b≥-2x,结合图象得到解集为:x≥-1.
22.(8分)22.(1)人数超过30人时,选乙宾馆更实惠些;(2)49人
【解析】
【分析】
(1)要想乙宾馆更实惠,人数首先要超过25人,设人数为x人,根据题意列出甲宾馆收费及乙宾馆收费,化简后再列出甲宾馆收费大于乙宾馆收费的不等式,求解后即可得出答案;
(2)根据题意,列出甲宾馆收费减去乙宾馆收费大于300的不等式,解出结果,并根据教师人数不到人即可确定教师的人数.
【详解】
(1)解:依题意得:要想乙宾馆更实惠,人数首先要超过25人,设人数为x人.
甲宾馆收费为:
乙宾馆收费为:
要乙宾馆更实惠些,则
当人数超过30人时,选乙宾馆更实惠些
(2)∵住乙宾馆比选甲宾馆可节省300多元
∴
∴
又∵x<50,
∴
答:此行教师有49人.
【点睛】
本题考查了不等式的应用及一次函数的应用,根据题意找到关系式是解题的关键.
23.(8分)23.(1)见解析;(2)见解析;(3).
【解析】
【分析】
(1)根据网格结构找出点、的位置,然后顺次连接即可;
(2)根据网格结构找出点的位置,然后连接即可;
(3)利用正方形的面积减去三个三角形的面积,列式计算即可得解.
【详解】
(1)线段如图所示;
(2)线段如图所示;
(3).
【点睛】
本题考查了平移变换和旋转变换作图,熟练掌握网格结构准确找出对应点的位置是解题的关键.
24.(10分)24.(1)购进甲种纪念品每件需100元,购进乙种纪念品每件需50元.(2)有三种进货方案.方案一:甲种纪念品60件,乙种纪念品20件;方案二:甲种纪念品61件,乙种纪念品19件;方案三:甲种纪念品62件,乙种纪念品18件.(3)若全部销售完,方案一获利最大,最大利润是1800元.
【解析】
【分析】
(1)设购进甲种纪念品每件价格为x元,乙种纪念币每件价格为y元,根据题意得出关于x和y的二元一次方程组,解方程组即可得出结论;
(2)设购进甲种纪念品a件,根据题意列出关于x的一元一次不等式,解不等式得出a的取值范围,即可得出结论;
(3)找出总利润关于购买甲种纪念品a件的函数关系式,由函数的增减性确定总利润取最值时a的值,从而得出结论.
【详解】
(1)设购进甲种纪念品每件需x元,购进乙种纪念品每件需y元.
由题意得:
,
解得:,
答:购进甲种纪念品每件需100元,购进乙种纪念品每件需50元.
(2)设购进甲种纪念品a(a≥60)件,则购进乙种纪念品(80﹣a)件.由题意得:
100a+50(80﹣a)≤7100
解得a≤62
又a≥60
所以a可取60、61、62.
即有三种进货方案.
方案一:甲种纪念品60件,乙种纪念品20件;
方案二:甲种纪念品61件,乙种纪念品19件;
方案三:甲种纪念品62件,乙种纪念品18件.
(3)设利润为W,则W=20a+30(80﹣a)=﹣10a+2400
所以W是a的一次函数,﹣10<0,W随a的增大而减小.
所以当a最小时,W最大.此时W=﹣10×60+2400=1800
答:若全部销售完,方案一获利最大,最大利润是1800元.
【点睛】
本题考查了二元一次方程组的应用,一元一次不等式的应用,一次函数的应用,找到相应的数量关系是解决问题的关键,注意第二问应求整数解,要求学生能够运用所学知识解决实际问题.
25.(10分)25.(1)A(﹣3,0),B(2,0),C(-5,2),D(0,2);(2)∠PQD+∠OPQ+∠POB=360°,理由见解析;(3)(2,0)或(﹣8,0)或(0,﹣)或(0,)
【解析】
【分析】
(1)根据绝对值的非负性、偶次方的非负性分别求出a、b,得到点A,B的坐标,即可解决问题;
(2)求出五边形QPOBD的内角和,根据平行线的性质得到∠QDB+∠OBD=180°,计算即可;
(3)根据题意求出△ACD的面积,分点M在x轴上、点M在y轴上两种情况,根据三角形的面积公式计算即可.
【详解】
解:(1)∵|2a+6|+(2a﹣3b+12)2=0,
∴|2a+6|=0,(2a﹣3b+12)2=0,
解得,a=﹣3,b=2,
则点A,B的坐标分别为A(﹣3,0),B(2,0);
将点A,B分别向左平移2个单位,再向上平移2个单位,分别得到点A,B的对应点C,D,则C(-5,2)D(0,2);
(2)∠PQD+∠OPQ+∠POB=360°,
理由如下:五边形QPOBD的内角和=(5﹣2)×180°=540°,
∵CD∥AB,
∴∠QDB+∠OBD=180°,
∴∠PQD+∠OPQ+∠POB=540°﹣(∠QDB+∠OBD)=360°;
(3)由题意得,点C的坐标为(﹣5,2),点D的坐标为(0,2),
则△ACD的面积=×5×2=5,
当点M在x轴上时,设点M的坐标为(x,0),
则AM=|﹣3﹣x|,
由题意得,×|﹣3﹣x|×2=5,
解得,x=2或﹣8,
当点M在y轴上时,设点M的坐标为(0,y),
则AM=|2﹣y|,
由题意得,×|2﹣y|×3=5,
解得,y=﹣或,
综上所述,三角形MAD的面积与三角形ACD的面积相等时,点M的坐标为(2,0)或(﹣8,0)或(0,﹣)或(0,).
【点睛】
本题考查的是非负数的性质、平移变换、三角形的面积计算,掌握坐标与图形的关系、灵活运用分情况讨论思想是解题的关键
(考试总分:120
分)
一、
单选题
(本题共计10小题,总分30分)
1.(3分)1.在下列四个标志中,既是中心对称又是轴对称图形的是( )
A.
B.
C.
D.
2.(3分)2.不等式2x>3-x的解集是(
)
A.x>3
B.x<3
C.x>1
D.x<1
3.(3分)3.一次函数y=kx+b(k,b是常数,k≠0)的图象如图所示,则不等式kx+b>0的解集是( )
A.x>0
B.x>3
C.x<0
D.x<3
4.(3分)4.不等式组的整数解共有( )
A.1个
B.2个
C.3个
D.4个
5.(3分)5.为有效开展“阳光体育”活动,某校计划购买篮球和足球共50个,购买资金不超过3000元.若每个篮球80元,每个足球50元,则篮球最多可购买(
)
A.16个
B.17个
C.33个
D.34个
6.(3分)6.若一次函数的图象经过点和,则不等式的解集为(
)
A.
B.
C.
D.
7.(3分)7.如果不等式的解集是,则a的取值范围是(
)
A.
B.
C.
D.
8.(3分)8.如图,中任意一点经平移后对应点为,将作同样的平移得到.则的坐标分别是(
)
A.
B.
C.
D.
9.(3分)9.如图,将三角形ABC沿BC方向平移3cm得到三角形DEF,若三角形ABC的周长为20cm,则四边形ABFD的周长为( )
A.23cm
B.26cm
C.29cm
D.32cm
10.(3分)10.如图,经过点B(1,0)的直线y=kx+b与直线y=4x+4相交于点A(m,),则0<kx+b<4x+4的解集为(
)
A.x<-
B.-<x<1
C.x<1
D.-1<x<1
二、
填空题
(本题共计8小题,总分24分)
11.(3分)11.不等式组:的解集为_____.
12.(3分)12.某次知识竞赛共有题,答对一题得分,答错或不答扣分,小华得分要超过分,他至少要答对__________题
13.(3分)13.如图,直线y=ax+1与y=﹣x+4交于点E,点A,B,C,D分别是两条直线与坐标轴的交点.则结论:①a>0;②点B的坐标是(0,1);
③S△BDE=3;④当x>2时,ax+1<﹣x+4中,正确的有_____.(只填序号)
14.(3分)14.点A(a,3)与点B(﹣4,b)关于原点对称,则a+b=_____.
15.(3分)15.如图,∠C=90°,将直角三角形ABC沿着射线BC方向平移6cm,得三角形A′B′C′,已知BC=3cm,AC=4cm,则阴影部分的面积为_____cm2.
16.(3分)16.如图,一次函数y1=x+b与一次函数y2=kx+4的图象交于点P(1,3),则关于x的不等式x+b>kx+4的解集是_____.
17.(3分)17.若关于的不等式组无解,
则的取值范围是
________.
18.(3分)18.如图,在平面直角坐标系中,将△ABO绕点A顺时针旋转到△AB1C1的位置,点B、O分别落在点B1、C1处,点B1在x轴上,再将△AB1C1绕点B1顺时针旋转到△A1B1C2的位置,点C2在x轴上,将△A1B1C2绕点C2顺时针旋转到△A2B2C2的位置,点A2在x轴上,依次进行下去….若点A(,0),B(0,4),则点B2014的横坐标为______.
三、
解答题
(本题共计7小题,总分66分)
19.(16分)19.解不等式(每题4分,共16分)
(1)
,
(2
)
(3)
(4)
20.(6分)20.()已知方程组,其中x为非正数,y为负数.
(1)求m的取值范围;
(2)不等式2mx+x<2m+1的解集为x>1,求m的整数值.
21.(8分)21.如图,直线y=-2x与直线y=kx+b相交于点A(a,2),并且直线y=kx+b经过x轴上点B(2,0).
(1)求直线y=kx+b的解析式;
(2)求两条直线与y轴围成的三角形面积;
(3)直接写出不等式(k+2)x+b≥0的解集.
22.(8分)22.某教育行政部门计划今年暑假组织部分教师到外地学习,预订宾馆住宿时,有住宿条件一样的甲、乙两家宾馆供选择,两家宾馆房源都很充足,其收费标准均为每人每天元,并且各自推出不同的优惠方案.甲宾馆是人(含人)以内的按标准收费,超过人的,超出部分按九折收费,乙宾馆是人(含人)以内的标准收费,超过人的,超出部分按八折收费.
(1)当人数超过多少人时,选乙宾馆更实惠些?
(2)此行教师人数不到人,选择住乙宾馆比选择住甲宾馆可节省少多元,问此行教师有多少人?
23.(8分)23.如图,方格纸上每个小正方形的边长均为1个单位长度,点A、B都在格点上(两条网格线的交点叫格点).
(1)将线段AB向上平移两个单位长度,点A的对应点为点,点B的对应点为点,请画出平移后的线段;
(2)将线段绕点按逆时针方向旋转,点的对应点为点,请画出旋转后的线段;
(3)连接、,求的面积.
24.(10分)24.某市正在举行文化艺术节活动,一商店抓住商机,决定购进甲,乙两种艺术节纪念品.若购进甲种纪念品4件,乙种纪念品3件,需要550元,若购进甲种纪念品5件,乙种纪念品6件,需要800元.
(1)求购进甲、乙两种纪念品每件各需多少元?
(2)若该商店决定购进这两种纪念品共80件,其中甲种纪念品的数量不少于60件.考虑到资金周转,用于购买这80件纪念品的资金不能超过7100元,那么该商店共有几种进货方案7
(3)若销售每件甲种纪含晶可获利润20元,每件乙种纪念品可获利润30元.在(2)中的各种进货方案中,若全部销售完,哪一种方案获利最大?最大利利润多少元?
25.(10分)25.如图1,在平面直角坐标系中,点A,B的坐标分别为A(a,0),B(b,0),且a,b满足|2a+6|+(2a﹣3b+12)2=0,现同时将点A,B分别向左平移2个单位,再向上平移2个单位,分别得到点A,B的对应点C,D,连接AC,BD.
(1)请直接写出A、B、C、D四点的坐标;
(2)如图2,点P是线段AC上的一个动点,点Q是线段CD的中点,连接PQ,PO,当点P在线段AC上移动时(不与A,C重合),请找出∠PQD,∠OPQ,∠POB的数量关系,并证明你的结论;
(3)在坐标轴上是否存在点M,使三角形MAD的面积与三角形ACD的面积相等?若存在,直接写出点M的坐标;若不存在,试说明理由.
答案
一、
单选题
(本题共计10小题,总分30分)
1.(3分)C
2.(3分)C
3.(3分)D
4.(3分)C
5.(3分)A
6.(3分)A
7.(3分)D
8.(3分)D
9.(3分)B
10.(3分)B
二、
填空题
(本题共计8小题,总分24分)
11.(3分)11.
12.(3分)12.9
13.(3分)13.①②③
14.(3分)14.1.
15.(3分)15.18
16.(3分)16.x>1.
17.(3分)17.
18.(3分)18.10070
三、
解答题
(本题共计7小题,总分66分)
19.(16分)19.x>-6,
;
不等式组的解集是﹣1≤x<2,在数轴上表示不等式组的解集见解析.
,非负整数解为和
20.(6分)20.(1);(2).
21.(8分)21.(1)一次函数的解析式是y=-x+;(2)S△ABC=;(3)x≥-1.
【解析】
试题分析:利用代入法求出点A的坐标,然后根据待定系数法求出一次函数的解析式;
(2)根据图像求出交点C的坐标,然后可求三角形的面积;
(3)根据图像的位置求出不等式的解集.
试题解析:解:(1)把A(a,2)代入y=-2x中,得-2a=2,∴a=-1,∴A(-1,2),把A(-1,2)、B(2,0)代入y=kx+b中得,∴k=-,b=,∴一次函数的解析式是y=-x+;
(2)设直线AB与y轴交于点C,则C(0,),∴S△ABC=××1=;
(3)不等式(k+2)x+b≥0可以变形为kx+b≥-2x,结合图象得到解集为:x≥-1.
22.(8分)22.(1)人数超过30人时,选乙宾馆更实惠些;(2)49人
【解析】
【分析】
(1)要想乙宾馆更实惠,人数首先要超过25人,设人数为x人,根据题意列出甲宾馆收费及乙宾馆收费,化简后再列出甲宾馆收费大于乙宾馆收费的不等式,求解后即可得出答案;
(2)根据题意,列出甲宾馆收费减去乙宾馆收费大于300的不等式,解出结果,并根据教师人数不到人即可确定教师的人数.
【详解】
(1)解:依题意得:要想乙宾馆更实惠,人数首先要超过25人,设人数为x人.
甲宾馆收费为:
乙宾馆收费为:
要乙宾馆更实惠些,则
当人数超过30人时,选乙宾馆更实惠些
(2)∵住乙宾馆比选甲宾馆可节省300多元
∴
∴
又∵x<50,
∴
答:此行教师有49人.
【点睛】
本题考查了不等式的应用及一次函数的应用,根据题意找到关系式是解题的关键.
23.(8分)23.(1)见解析;(2)见解析;(3).
【解析】
【分析】
(1)根据网格结构找出点、的位置,然后顺次连接即可;
(2)根据网格结构找出点的位置,然后连接即可;
(3)利用正方形的面积减去三个三角形的面积,列式计算即可得解.
【详解】
(1)线段如图所示;
(2)线段如图所示;
(3).
【点睛】
本题考查了平移变换和旋转变换作图,熟练掌握网格结构准确找出对应点的位置是解题的关键.
24.(10分)24.(1)购进甲种纪念品每件需100元,购进乙种纪念品每件需50元.(2)有三种进货方案.方案一:甲种纪念品60件,乙种纪念品20件;方案二:甲种纪念品61件,乙种纪念品19件;方案三:甲种纪念品62件,乙种纪念品18件.(3)若全部销售完,方案一获利最大,最大利润是1800元.
【解析】
【分析】
(1)设购进甲种纪念品每件价格为x元,乙种纪念币每件价格为y元,根据题意得出关于x和y的二元一次方程组,解方程组即可得出结论;
(2)设购进甲种纪念品a件,根据题意列出关于x的一元一次不等式,解不等式得出a的取值范围,即可得出结论;
(3)找出总利润关于购买甲种纪念品a件的函数关系式,由函数的增减性确定总利润取最值时a的值,从而得出结论.
【详解】
(1)设购进甲种纪念品每件需x元,购进乙种纪念品每件需y元.
由题意得:
,
解得:,
答:购进甲种纪念品每件需100元,购进乙种纪念品每件需50元.
(2)设购进甲种纪念品a(a≥60)件,则购进乙种纪念品(80﹣a)件.由题意得:
100a+50(80﹣a)≤7100
解得a≤62
又a≥60
所以a可取60、61、62.
即有三种进货方案.
方案一:甲种纪念品60件,乙种纪念品20件;
方案二:甲种纪念品61件,乙种纪念品19件;
方案三:甲种纪念品62件,乙种纪念品18件.
(3)设利润为W,则W=20a+30(80﹣a)=﹣10a+2400
所以W是a的一次函数,﹣10<0,W随a的增大而减小.
所以当a最小时,W最大.此时W=﹣10×60+2400=1800
答:若全部销售完,方案一获利最大,最大利润是1800元.
【点睛】
本题考查了二元一次方程组的应用,一元一次不等式的应用,一次函数的应用,找到相应的数量关系是解决问题的关键,注意第二问应求整数解,要求学生能够运用所学知识解决实际问题.
25.(10分)25.(1)A(﹣3,0),B(2,0),C(-5,2),D(0,2);(2)∠PQD+∠OPQ+∠POB=360°,理由见解析;(3)(2,0)或(﹣8,0)或(0,﹣)或(0,)
【解析】
【分析】
(1)根据绝对值的非负性、偶次方的非负性分别求出a、b,得到点A,B的坐标,即可解决问题;
(2)求出五边形QPOBD的内角和,根据平行线的性质得到∠QDB+∠OBD=180°,计算即可;
(3)根据题意求出△ACD的面积,分点M在x轴上、点M在y轴上两种情况,根据三角形的面积公式计算即可.
【详解】
解:(1)∵|2a+6|+(2a﹣3b+12)2=0,
∴|2a+6|=0,(2a﹣3b+12)2=0,
解得,a=﹣3,b=2,
则点A,B的坐标分别为A(﹣3,0),B(2,0);
将点A,B分别向左平移2个单位,再向上平移2个单位,分别得到点A,B的对应点C,D,则C(-5,2)D(0,2);
(2)∠PQD+∠OPQ+∠POB=360°,
理由如下:五边形QPOBD的内角和=(5﹣2)×180°=540°,
∵CD∥AB,
∴∠QDB+∠OBD=180°,
∴∠PQD+∠OPQ+∠POB=540°﹣(∠QDB+∠OBD)=360°;
(3)由题意得,点C的坐标为(﹣5,2),点D的坐标为(0,2),
则△ACD的面积=×5×2=5,
当点M在x轴上时,设点M的坐标为(x,0),
则AM=|﹣3﹣x|,
由题意得,×|﹣3﹣x|×2=5,
解得,x=2或﹣8,
当点M在y轴上时,设点M的坐标为(0,y),
则AM=|2﹣y|,
由题意得,×|2﹣y|×3=5,
解得,y=﹣或,
综上所述,三角形MAD的面积与三角形ACD的面积相等时,点M的坐标为(2,0)或(﹣8,0)或(0,﹣)或(0,).
【点睛】
本题考查的是非负数的性质、平移变换、三角形的面积计算,掌握坐标与图形的关系、灵活运用分情况讨论思想是解题的关键
同课章节目录
