13.4最短路径问题同步课时训练 2021-2022学年 人教版版八年级上册 (广东地区 )(Word版含解析)
文档属性
| 名称 | 13.4最短路径问题同步课时训练 2021-2022学年 人教版版八年级上册 (广东地区 )(Word版含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 595.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-16 10:32:30 | ||
图片预览



文档简介
2021-2022学年第一学期同步课时训练(广东地区人教版专用)
13.4最短路径问题
一、单选题(在下列各题的四个选项中,只有一项是符合题意的.本题共8个小题)
1.(2020·全国测试)如图,中,,,,,是的平分线.若P、Q分别是和上的动点,则的最小值是(
)
A.
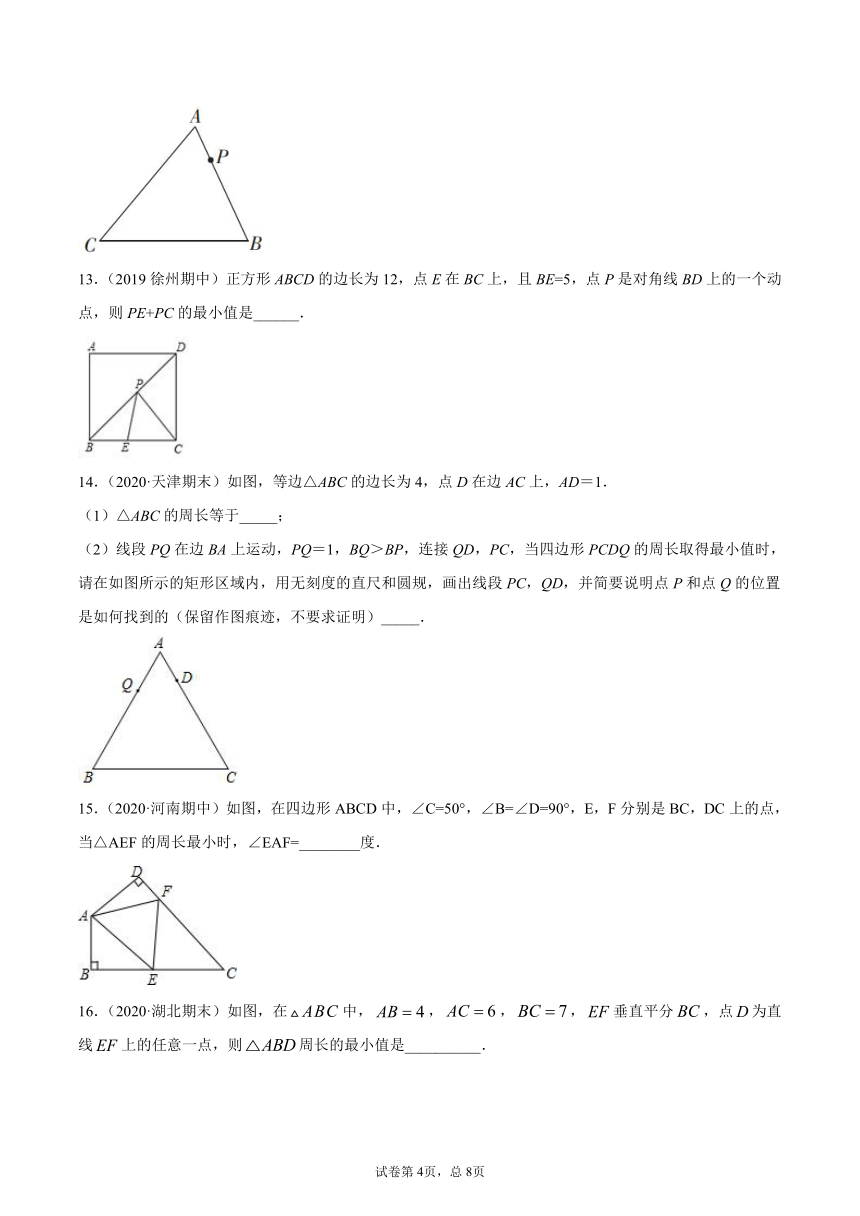
B.4
C.
D.5
2.(2020·广东期末)下列说法正确的是(
)
A.如果两个角相等,那么这两个角是对顶角
B.经过一点有且只有一条直线与已知直线平行
C.如果两条直线被第三条直线所截,那么内错角相等
D.联结直线外一点与直线上各点的所有线段中,垂线段最短
3.(2019·广东期中)如图,在△ABC中,AB=AC,BC=4,△ABC的面积是16,AC边的垂直平分线EF分别交AC,AB边于点E,F,若点D为BC边的中点,点M为线段EF上一动点,则△CDM周长的最小值为(?)
A.4
B.5
C.10
D.8
4.(2019·广州期中)如图,直线l是一条河,A、B
是两个新农村定居点.欲在
l
上的某点处修建一个水泵站,由水泵站直接向
A、B两地供水.现有如下四种管道铺设方案,图中实线表示铺设的供水管道,则铺设管
道最短的方案是(
)
A.
B.C.
D.
5.(2020·深圳期中)如图是一个正方体,小敏同学经过研究得到如下5个结论,正确的结论有(
)个
①用剪刀沿着它的棱剪开这个纸盒,至少要剪7刀,才能展开成平面图形;②用一平面去截这个正方体得到的截面是三角形ABC,则∠ABC=45°;③一只蚂蚁在一个实心正方体木块P点处想沿着表面爬到C点最近的路只有4条;④用一平面去截这个正方体得到的截面可能是八边形;⑤正方体平面展开图有11种不同的图形.
A.1
B.2
C.3
D.4
6.(2019·佛山期中)某开发商的经适房的三个居民小区A、B、C在同一条直线上,位置如图所示.其中小区B到小区A、C的距离分别是70m和150m,现在想在小区A、C之间建立一个超市,要求各小区居民到超市总路程的和最小,那么超市的位置应建在( )
A.小区A
B.小区B
C.小区C
D.AC的中点
7.(2019·阳江期中)如图,点P是直线a外一点,PB⊥a,点A,B,C,D都在直线a上,下列线段中最短的是(
)
A.PA
B.PB
C.PC
D.PD
8.(2020·广州期末)如图,某工厂有三个住宅区,A、B、C各区分别住有职工15人、20人、45人,且这三个区在一条大道上(A、B、C三点共线),已知AB=1500m,BC=1000m,为了方便职工上下班,该工厂打算从以下四处中选一处设置接送车停靠点,为使所有的人步行到停靠点的路程之和最小,那么该停靠点的位置应设在( )
A.A住宅区
B.B住宅区
C.C住宅区
D.B、C住宅区中间D处
二、填空题(本题共9个小题)
9.(2020·沈阳期末)如图,等边△ABC中,BD⊥AC于点D,AD=3.5cm,点P、Q分别为AB、AD上的两个定点且BP=AQ=2cm,若在BD上有一动点E使PE+QE最短,则PE+QE的最小值为_____cm
10.(2020·广州期中)如图,AD为等边△ABC的高,E、F分别为线段AD、AC上的动点,且AE=CF,当BF+CE取得最小值时,∠AFB=_______°.
11.(2020东广期末)如图,在△ABC中,AB=AC=5,BC=6,AD是∠BAC的平分线,AD=4.若P,Q分别是AD和AC上的动点,则PC+PQ的最小值是_____.
12.(2020·湖北期末)如图,在锐角中,,边上有一定点分别是和边上的动点,当的周长最小时,的度数是_________.
13.(2019徐州期中)正方形ABCD的边长为12,点E在BC上,且BE=5,点P是对角线BD上的一个动点,则PE+PC的最小值是______.
14.(2020·天津期末)如图,等边△ABC的边长为4,点D在边AC上,AD=1.
(1)△ABC的周长等于_____;
(2)线段PQ在边BA上运动,PQ=1,BQ>BP,连接QD,PC,当四边形PCDQ的周长取得最小值时,请在如图所示的矩形区域内,用无刻度的直尺和圆规,画出线段PC,QD,并简要说明点P和点Q的位置是如何找到的(保留作图痕迹,不要求证明)_____.
15.(2020·河南期中)如图,在四边形ABCD中,∠C=50°,∠B=∠D=90°,E,F分别是BC,DC上的点,当△AEF的周长最小时,∠EAF=________度.
16.(2020·湖北期末)如图,在中,,,,垂直平分,点为直线上的任意一点,则周长的最小值是__________.
17.(2019·山西期中)已知点和点,若点在轴上,则的最小值为__________.
三、解答题(本题共8个小题,解答应写出文字说明、证明过程或演算步骤)
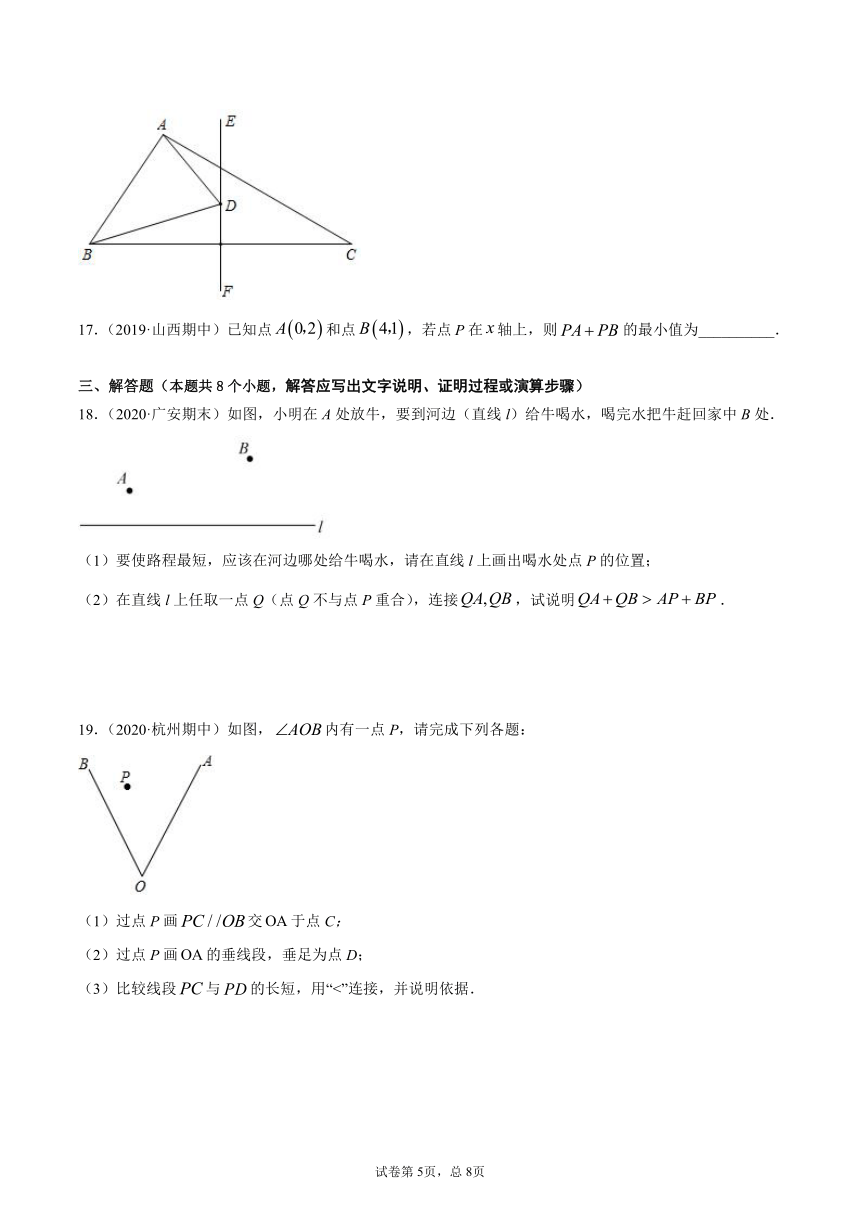
18.(2020·广安期末)如图,小明在A处放牛,要到河边(直线l)给牛喝水,喝完水把牛赶回家中B处.
(1)要使路程最短,应该在河边哪处给牛喝水,请在直线l上画出喝水处点P的位置;
(2)在直线l上任取一点Q(点Q不与点P重合),连接,试说明.
19.(2020·杭州期中)如图,内有一点P,请完成下列各题:
(1)过点P画交于点C;
(2)过点P画的垂线段,垂足为点D;
(3)比较线段与的长短,用“<”连接,并说明依据.
20.(2020·鞍山期中)如图,BA、BC是两条公路,在两条公路夹角内部的点P处有一油库,若在两公路上分别建个加油站,并使运油的油罐车从油库出发先到一加油站,再到另一加油站,最后回到油库的路程最短,则加油站应如何选址?
21.(2020·日照期末)如图,△ABC的三个顶点在边长为1的正方形网格中,已知A(?4,5),B(﹣3,1),C(?2,3).
(1)画出△ABC及关于y轴对称的△A1B1C1,其中点B1的坐标是________;
(2)若点M是x轴上的动点,在图中画出使△B1CM周长最小时的点M.
22.(2020·盘锦期末)如图,要在燃气管道上修建一个泵站,分别向A、B两镇供气,请你利用尺规作图帮助确定泵站P修在什么地方,可使所用的输气管线最短?(保留作图痕迹,不写作法)
23.(2019·肇庆月考)如图,A、B是两个蓄水池,都在河流a的同侧,为了方便灌溉作物,要在河边建一个抽水站,将河水送到A、B两地,问该站建在河边什么地方,可使所修的渠道最短,试在图中确定该点.(保留作图痕迹)
24.(2020·东莞期末)如图,在平面直角坐标系中,,,.
(1)作出关于轴的对称图形;
(2)写出点,,的坐标;
(3)在轴上找一点,使最短(不写作法).
25.(2018·广州期末)在如图所示的方格纸中,
(1)作出△ABC关于MN对称的图形△A1B1C1.
(2)说明△A2B2C2可以由△A1B1C1经过怎样的平移变换得到?
(3)以MN所在直线为x轴,AA1的中点为坐标原点,建立直角坐标系xOy,试在x轴上找一点P,使得PA1+PB2最小,直接写出点P的坐标.
试卷第1页,总3页
试卷第1页,总3页
参考答案
1.【解析】在BC上截取,连接,如图,
∵是的平分线,∴∠ABD=∠CBD,
在△PBQ和中,
∴△△PBQ≌(SAS),
∴,
∴,
∴当A、P、三点共线且时,的值最小,
过点A作AF⊥BC于点F,则的最小值即为AF的长,
∵,
∴,
即的最小值为.
故选C.
2.【解析】A.
如果两个角相等,那么这两个角不一定是对顶角,选项错误,不符合题意;
B.
经过直线外一点有且只有一条直线与已知直线平行,选项错误,不符合题意;
C.
如果两条平行线被第三条直线所截,那么内错角相等,选项错误,不符合题意;
D.
联结直线外一点与直线上各点的所有线段中,垂线段最短,选项正确,符合题意;
故选:D.
3.【解析】连接AD,AM.
∵△ABC是等腰三角形,点D是BC边的中点,
∴AD⊥BC,
∴S△ABC=BC?AD=×4×AD=16,解得AD=8,
∵EF是线段AC的垂直平分线,
∴点C关于直线EF的对称点为点A,
∴MA=MC,
∵AD≤AM+MD,
∴AD的长为CM+MD的最小值,
∴△CDM的周长最短=(CM+MD)+CD=AD+BC=8+×4=8+2=10.
故选C.
4.【解析】作点A关于直线l的对称点A′,连接BA′交直线l于M.
根据两点之间,线段最短,可知选项D铺设的管道,则所需管道最短.
故选D.
5.【解析】(1)AB、BC、AC均是相同正方形的对角线,故AB=BC=AC,△ABC是等边三角形,∠ABC=60°,②错误;
(2)用一平面去截n棱柱,截面最多是(n+2)边形,正方体是四棱柱,所以截面最多是六边形,④错误;
(3)正方体的展开图只有11种,⑤正确;
(4)正方体的11种展开图,六个小正方形均是一连一关系,即必须是5条边相连,正方体有12条棱,所以要剪12-5=7条棱,才能把正方体展开成平面图形,①正确;
(5)正方体有六个面,P点属于“前、左、下面”这三个面,所以从P到C,可以走“前+上、前+右、左+上、左+后、下+右、下+后”这六处组合的面,这其中任何一个组合的两个面展开均是相同的长方形,而P到C的最短路线是这个长方形的对角线,这些对角线均相等,故从P到C的最短路线有6条;③错误.
综上所述,正确的选项是①⑤,
故选B
6.【解析】设超市为点P,
∵P点在A、C
之间,
∴AP+BP+CP是超市到小区居民总路程的和,
∵AP+CP=AC,
∴当PB最短时,即P点与B点重合时,AP+BP+CP=AC,此时市到小区居民总路程的和最小,
故选:B.
7.【解析】如图,PB是点P到a的垂线段,
∴线段中最短的是PB.
故选B.
8.【解析】当停靠点在A区时,所有员工步行到停靠点路程和是:20×1500+45×2500=142500m;
当停靠点在B区时,所有员工步行到停靠点路程和是:15×1500+45×1000=67500m;
当停靠点在C区时,所有员工步行到停靠点路程和是:15×2500+20×1000=57500m;
当停靠点在D区时,设距离B区x米,所有员工步行到停靠点路程和是:15×2000+20×500+45×500=62500m.
∴当停靠点在C区时,所有员工步行到停靠点路程和最小.
故选:C.
9.【解析】
如图,过BD作P的对称点,连接P,Q,Q与BD交于一点E,再连接PE,此时PE+QE最小.
∵与P关于BD对称,
∴PE=E,BP=B=2cm,
∴PE+QE=
Q,
又∵等边△ABC中,BD⊥AC于点D,AD=3.5cm,
∴AC=BC=AB=7cm,
∵BP=AQ=2cm,
∴QC=5cm,
∵B=2cm,
∴C=5cm,
∴△Q
C为等边三角形,
∴Q=5cm.
∴PE+QE=5cm.
所以答案为5.
10.105°
【解析】如图,作CH⊥BC,且CH=BC,连接BH交AD于M,连接FH,
∵△ABC是等边三角形,AD⊥BC,
∴AC=BC,∠DAC=30°,
∴AC=CH,
∵∠BCH=90°,∠ACB=60°,
∴∠ACH=90°?60°=30°,
∴∠DAC=∠ACH=30°,
∵AE=CF,
∴△AEC≌△CFH,
∴CE=FH,BF+CE=BF+FH,
∴当F为AC与BH的交点时,BF+CE的值最小,
此时∠FBC=45°,∠FCB=60°,
∴∠AFB=105°,
故答案为105°.
11.【解析】∵AB=AC,AD是∠BAC的平分线,
∴AD垂直平分BC,
∴BP=CP.
如图,过点B作BQ⊥AC于点Q,BQ交AD于点P,则此时PC+PQ取最小值,最小值为BQ的长,
∵S△ABC=BC?AD=AC?BQ,
∴BQ==,
即PC+PQ的最小值是.
故答案为.
【点睛】
本题考查了轴对称﹣最短路线问题、等腰三角形的性质以及三角形的面积,凡是涉及最短距离的问题,一般要考虑线段的性质定理,结合轴对称变换来解决,多数情况要作点关于某直线的对称点.
12.【解析】∵
PD⊥AC,PG⊥BC,
∴∠PEC=∠PFC=90°,
∴
∠C+∠EPF=180°,
∵∠C=50°,
∵∠D+∠G+∠EPF=180°,
∴
∠D+∠G=50°,
由对称可知:∠G=∠GPN,∠D=∠DPM,
L
∴∠GPN+∠DPM=50°,
∴∠MPN=130°-50°=80°,
故答案为:80°.
13.【解析】如图连接AE交BD于P点,
则AE就是PE+PC的最小值,
∵正方形ABCD中,点E是BC上的一定点,且BE=5,
∵AB=12,
∴AE==13,
∴PE+PC的最小值是13.
故答案为:13.
14.【解析】(1)△ABC的周长等于,故答案为:12;
(2)如图:
故答案为:过点C作CE∥AB,且CE=1,作点D关于AB的对称点F,连接EF交AB于一点为Q,在AB上BQ之间截取PQ=1,连接CP、DQ,则四边形PCDQ为所求的周长最小的四边形.
.
15.【解析】作A关于BC和CD的对称点A′,A″,连接A′A″,交BC于E,交CD于F,则A′A″即为△AEF的周长最小值.作DA延长线AH,
∵∠C=50°,
∴∠DAB=130°,
∴∠HAA′=50°,
∴∠A′+∠A″=∠HAA′=50°,
∵∠A′=∠EAB,∠A″=∠FAD,
∴∠EAB+∠FAD=50°,
∴∠EAF=130°-50°=80°,
故答案为80°.
16.【解析】∵垂直平分,
∴点与点关于对称,
如图,设与相交于点,
∴当和重合时,的值最小,最小值等于的长,
∵,,
∴的周长的最小值是,
故答案为:10.
17.【解析】作点A关于x轴的对称点A′,连接A′B交x轴于点P,则P即为所求点;
∵点A(0,2),
∴点A关于x轴的对称点A′的坐标为(0,-2),
∵A′(0,-2),B(4,1),
∴A′B==5.
即PA+PB的最小值为5.
故答案为5.
18.【解析】(1)如图,点P即为所求.
(2)如图,在直线l上任取一点Q,连接.
∵点A与关于直线l对称,点P,Q在直线l上,
∴.
∵,
∴,即,
∴.
19.【解析】
(1)如图,PC即为所画;
(2)如图,PD即为所画;
(3)由垂线段最短可知:PC>PD.
20.【解析】如图所示:C、D点即为所求.
21.【解析】(1)如图所示;根据图形可知B1(3,2),
故答案为:(3,2);
(2)如图所示:找C关于x轴的对称点C′,则C′(-2,-3),,
连接交x轴于一点M,根据两点之间线段最短,可知此时的M即为使周长最小时的点M.
22.【解析】画出图形如图所示,点P即为泵站的位置.
23.作点A关于直线a对称的点C,连接BC交a于点P,则点P就是抽水站的位置.
【解析】将在直线同侧的两个点分到直线的异侧,两点间线段最短
24.【解析】(1)如图所示,为所求作.
(2)由图可得,,,.
(3)如图所示,点即为所求作.
25.【解析】(1)如图所示,△A1B1C1即为所求;
(2)△A2B2C2可以由△A1B1C1向右平移6个单位,向下平移2个单位得到;
(3)如图,连接AB2,交x轴于P,连接A1P,则PA1+PB2最小,
此时,点P的坐标为(1,0).
答案第1页,总2页
答案第1页,总2页
13.4最短路径问题
一、单选题(在下列各题的四个选项中,只有一项是符合题意的.本题共8个小题)
1.(2020·全国测试)如图,中,,,,,是的平分线.若P、Q分别是和上的动点,则的最小值是(
)
A.
B.4
C.
D.5
2.(2020·广东期末)下列说法正确的是(
)
A.如果两个角相等,那么这两个角是对顶角
B.经过一点有且只有一条直线与已知直线平行
C.如果两条直线被第三条直线所截,那么内错角相等
D.联结直线外一点与直线上各点的所有线段中,垂线段最短
3.(2019·广东期中)如图,在△ABC中,AB=AC,BC=4,△ABC的面积是16,AC边的垂直平分线EF分别交AC,AB边于点E,F,若点D为BC边的中点,点M为线段EF上一动点,则△CDM周长的最小值为(?)
A.4
B.5
C.10
D.8
4.(2019·广州期中)如图,直线l是一条河,A、B
是两个新农村定居点.欲在
l
上的某点处修建一个水泵站,由水泵站直接向
A、B两地供水.现有如下四种管道铺设方案,图中实线表示铺设的供水管道,则铺设管
道最短的方案是(
)
A.
B.C.
D.
5.(2020·深圳期中)如图是一个正方体,小敏同学经过研究得到如下5个结论,正确的结论有(
)个
①用剪刀沿着它的棱剪开这个纸盒,至少要剪7刀,才能展开成平面图形;②用一平面去截这个正方体得到的截面是三角形ABC,则∠ABC=45°;③一只蚂蚁在一个实心正方体木块P点处想沿着表面爬到C点最近的路只有4条;④用一平面去截这个正方体得到的截面可能是八边形;⑤正方体平面展开图有11种不同的图形.
A.1
B.2
C.3
D.4
6.(2019·佛山期中)某开发商的经适房的三个居民小区A、B、C在同一条直线上,位置如图所示.其中小区B到小区A、C的距离分别是70m和150m,现在想在小区A、C之间建立一个超市,要求各小区居民到超市总路程的和最小,那么超市的位置应建在( )
A.小区A
B.小区B
C.小区C
D.AC的中点
7.(2019·阳江期中)如图,点P是直线a外一点,PB⊥a,点A,B,C,D都在直线a上,下列线段中最短的是(
)
A.PA
B.PB
C.PC
D.PD
8.(2020·广州期末)如图,某工厂有三个住宅区,A、B、C各区分别住有职工15人、20人、45人,且这三个区在一条大道上(A、B、C三点共线),已知AB=1500m,BC=1000m,为了方便职工上下班,该工厂打算从以下四处中选一处设置接送车停靠点,为使所有的人步行到停靠点的路程之和最小,那么该停靠点的位置应设在( )
A.A住宅区
B.B住宅区
C.C住宅区
D.B、C住宅区中间D处
二、填空题(本题共9个小题)
9.(2020·沈阳期末)如图,等边△ABC中,BD⊥AC于点D,AD=3.5cm,点P、Q分别为AB、AD上的两个定点且BP=AQ=2cm,若在BD上有一动点E使PE+QE最短,则PE+QE的最小值为_____cm
10.(2020·广州期中)如图,AD为等边△ABC的高,E、F分别为线段AD、AC上的动点,且AE=CF,当BF+CE取得最小值时,∠AFB=_______°.
11.(2020东广期末)如图,在△ABC中,AB=AC=5,BC=6,AD是∠BAC的平分线,AD=4.若P,Q分别是AD和AC上的动点,则PC+PQ的最小值是_____.
12.(2020·湖北期末)如图,在锐角中,,边上有一定点分别是和边上的动点,当的周长最小时,的度数是_________.
13.(2019徐州期中)正方形ABCD的边长为12,点E在BC上,且BE=5,点P是对角线BD上的一个动点,则PE+PC的最小值是______.
14.(2020·天津期末)如图,等边△ABC的边长为4,点D在边AC上,AD=1.
(1)△ABC的周长等于_____;
(2)线段PQ在边BA上运动,PQ=1,BQ>BP,连接QD,PC,当四边形PCDQ的周长取得最小值时,请在如图所示的矩形区域内,用无刻度的直尺和圆规,画出线段PC,QD,并简要说明点P和点Q的位置是如何找到的(保留作图痕迹,不要求证明)_____.
15.(2020·河南期中)如图,在四边形ABCD中,∠C=50°,∠B=∠D=90°,E,F分别是BC,DC上的点,当△AEF的周长最小时,∠EAF=________度.
16.(2020·湖北期末)如图,在中,,,,垂直平分,点为直线上的任意一点,则周长的最小值是__________.
17.(2019·山西期中)已知点和点,若点在轴上,则的最小值为__________.
三、解答题(本题共8个小题,解答应写出文字说明、证明过程或演算步骤)
18.(2020·广安期末)如图,小明在A处放牛,要到河边(直线l)给牛喝水,喝完水把牛赶回家中B处.
(1)要使路程最短,应该在河边哪处给牛喝水,请在直线l上画出喝水处点P的位置;
(2)在直线l上任取一点Q(点Q不与点P重合),连接,试说明.
19.(2020·杭州期中)如图,内有一点P,请完成下列各题:
(1)过点P画交于点C;
(2)过点P画的垂线段,垂足为点D;
(3)比较线段与的长短,用“<”连接,并说明依据.
20.(2020·鞍山期中)如图,BA、BC是两条公路,在两条公路夹角内部的点P处有一油库,若在两公路上分别建个加油站,并使运油的油罐车从油库出发先到一加油站,再到另一加油站,最后回到油库的路程最短,则加油站应如何选址?
21.(2020·日照期末)如图,△ABC的三个顶点在边长为1的正方形网格中,已知A(?4,5),B(﹣3,1),C(?2,3).
(1)画出△ABC及关于y轴对称的△A1B1C1,其中点B1的坐标是________;
(2)若点M是x轴上的动点,在图中画出使△B1CM周长最小时的点M.
22.(2020·盘锦期末)如图,要在燃气管道上修建一个泵站,分别向A、B两镇供气,请你利用尺规作图帮助确定泵站P修在什么地方,可使所用的输气管线最短?(保留作图痕迹,不写作法)
23.(2019·肇庆月考)如图,A、B是两个蓄水池,都在河流a的同侧,为了方便灌溉作物,要在河边建一个抽水站,将河水送到A、B两地,问该站建在河边什么地方,可使所修的渠道最短,试在图中确定该点.(保留作图痕迹)
24.(2020·东莞期末)如图,在平面直角坐标系中,,,.
(1)作出关于轴的对称图形;
(2)写出点,,的坐标;
(3)在轴上找一点,使最短(不写作法).
25.(2018·广州期末)在如图所示的方格纸中,
(1)作出△ABC关于MN对称的图形△A1B1C1.
(2)说明△A2B2C2可以由△A1B1C1经过怎样的平移变换得到?
(3)以MN所在直线为x轴,AA1的中点为坐标原点,建立直角坐标系xOy,试在x轴上找一点P,使得PA1+PB2最小,直接写出点P的坐标.
试卷第1页,总3页
试卷第1页,总3页
参考答案
1.【解析】在BC上截取,连接,如图,
∵是的平分线,∴∠ABD=∠CBD,
在△PBQ和中,
∴△△PBQ≌(SAS),
∴,
∴,
∴当A、P、三点共线且时,的值最小,
过点A作AF⊥BC于点F,则的最小值即为AF的长,
∵,
∴,
即的最小值为.
故选C.
2.【解析】A.
如果两个角相等,那么这两个角不一定是对顶角,选项错误,不符合题意;
B.
经过直线外一点有且只有一条直线与已知直线平行,选项错误,不符合题意;
C.
如果两条平行线被第三条直线所截,那么内错角相等,选项错误,不符合题意;
D.
联结直线外一点与直线上各点的所有线段中,垂线段最短,选项正确,符合题意;
故选:D.
3.【解析】连接AD,AM.
∵△ABC是等腰三角形,点D是BC边的中点,
∴AD⊥BC,
∴S△ABC=BC?AD=×4×AD=16,解得AD=8,
∵EF是线段AC的垂直平分线,
∴点C关于直线EF的对称点为点A,
∴MA=MC,
∵AD≤AM+MD,
∴AD的长为CM+MD的最小值,
∴△CDM的周长最短=(CM+MD)+CD=AD+BC=8+×4=8+2=10.
故选C.
4.【解析】作点A关于直线l的对称点A′,连接BA′交直线l于M.
根据两点之间,线段最短,可知选项D铺设的管道,则所需管道最短.
故选D.
5.【解析】(1)AB、BC、AC均是相同正方形的对角线,故AB=BC=AC,△ABC是等边三角形,∠ABC=60°,②错误;
(2)用一平面去截n棱柱,截面最多是(n+2)边形,正方体是四棱柱,所以截面最多是六边形,④错误;
(3)正方体的展开图只有11种,⑤正确;
(4)正方体的11种展开图,六个小正方形均是一连一关系,即必须是5条边相连,正方体有12条棱,所以要剪12-5=7条棱,才能把正方体展开成平面图形,①正确;
(5)正方体有六个面,P点属于“前、左、下面”这三个面,所以从P到C,可以走“前+上、前+右、左+上、左+后、下+右、下+后”这六处组合的面,这其中任何一个组合的两个面展开均是相同的长方形,而P到C的最短路线是这个长方形的对角线,这些对角线均相等,故从P到C的最短路线有6条;③错误.
综上所述,正确的选项是①⑤,
故选B
6.【解析】设超市为点P,
∵P点在A、C
之间,
∴AP+BP+CP是超市到小区居民总路程的和,
∵AP+CP=AC,
∴当PB最短时,即P点与B点重合时,AP+BP+CP=AC,此时市到小区居民总路程的和最小,
故选:B.
7.【解析】如图,PB是点P到a的垂线段,
∴线段中最短的是PB.
故选B.
8.【解析】当停靠点在A区时,所有员工步行到停靠点路程和是:20×1500+45×2500=142500m;
当停靠点在B区时,所有员工步行到停靠点路程和是:15×1500+45×1000=67500m;
当停靠点在C区时,所有员工步行到停靠点路程和是:15×2500+20×1000=57500m;
当停靠点在D区时,设距离B区x米,所有员工步行到停靠点路程和是:15×2000+20×500+45×500=62500m.
∴当停靠点在C区时,所有员工步行到停靠点路程和最小.
故选:C.
9.【解析】
如图,过BD作P的对称点,连接P,Q,Q与BD交于一点E,再连接PE,此时PE+QE最小.
∵与P关于BD对称,
∴PE=E,BP=B=2cm,
∴PE+QE=
Q,
又∵等边△ABC中,BD⊥AC于点D,AD=3.5cm,
∴AC=BC=AB=7cm,
∵BP=AQ=2cm,
∴QC=5cm,
∵B=2cm,
∴C=5cm,
∴△Q
C为等边三角形,
∴Q=5cm.
∴PE+QE=5cm.
所以答案为5.
10.105°
【解析】如图,作CH⊥BC,且CH=BC,连接BH交AD于M,连接FH,
∵△ABC是等边三角形,AD⊥BC,
∴AC=BC,∠DAC=30°,
∴AC=CH,
∵∠BCH=90°,∠ACB=60°,
∴∠ACH=90°?60°=30°,
∴∠DAC=∠ACH=30°,
∵AE=CF,
∴△AEC≌△CFH,
∴CE=FH,BF+CE=BF+FH,
∴当F为AC与BH的交点时,BF+CE的值最小,
此时∠FBC=45°,∠FCB=60°,
∴∠AFB=105°,
故答案为105°.
11.【解析】∵AB=AC,AD是∠BAC的平分线,
∴AD垂直平分BC,
∴BP=CP.
如图,过点B作BQ⊥AC于点Q,BQ交AD于点P,则此时PC+PQ取最小值,最小值为BQ的长,
∵S△ABC=BC?AD=AC?BQ,
∴BQ==,
即PC+PQ的最小值是.
故答案为.
【点睛】
本题考查了轴对称﹣最短路线问题、等腰三角形的性质以及三角形的面积,凡是涉及最短距离的问题,一般要考虑线段的性质定理,结合轴对称变换来解决,多数情况要作点关于某直线的对称点.
12.【解析】∵
PD⊥AC,PG⊥BC,
∴∠PEC=∠PFC=90°,
∴
∠C+∠EPF=180°,
∵∠C=50°,
∵∠D+∠G+∠EPF=180°,
∴
∠D+∠G=50°,
由对称可知:∠G=∠GPN,∠D=∠DPM,
L
∴∠GPN+∠DPM=50°,
∴∠MPN=130°-50°=80°,
故答案为:80°.
13.【解析】如图连接AE交BD于P点,
则AE就是PE+PC的最小值,
∵正方形ABCD中,点E是BC上的一定点,且BE=5,
∵AB=12,
∴AE==13,
∴PE+PC的最小值是13.
故答案为:13.
14.【解析】(1)△ABC的周长等于,故答案为:12;
(2)如图:
故答案为:过点C作CE∥AB,且CE=1,作点D关于AB的对称点F,连接EF交AB于一点为Q,在AB上BQ之间截取PQ=1,连接CP、DQ,则四边形PCDQ为所求的周长最小的四边形.
.
15.【解析】作A关于BC和CD的对称点A′,A″,连接A′A″,交BC于E,交CD于F,则A′A″即为△AEF的周长最小值.作DA延长线AH,
∵∠C=50°,
∴∠DAB=130°,
∴∠HAA′=50°,
∴∠A′+∠A″=∠HAA′=50°,
∵∠A′=∠EAB,∠A″=∠FAD,
∴∠EAB+∠FAD=50°,
∴∠EAF=130°-50°=80°,
故答案为80°.
16.【解析】∵垂直平分,
∴点与点关于对称,
如图,设与相交于点,
∴当和重合时,的值最小,最小值等于的长,
∵,,
∴的周长的最小值是,
故答案为:10.
17.【解析】作点A关于x轴的对称点A′,连接A′B交x轴于点P,则P即为所求点;
∵点A(0,2),
∴点A关于x轴的对称点A′的坐标为(0,-2),
∵A′(0,-2),B(4,1),
∴A′B==5.
即PA+PB的最小值为5.
故答案为5.
18.【解析】(1)如图,点P即为所求.
(2)如图,在直线l上任取一点Q,连接.
∵点A与关于直线l对称,点P,Q在直线l上,
∴.
∵,
∴,即,
∴.
19.【解析】
(1)如图,PC即为所画;
(2)如图,PD即为所画;
(3)由垂线段最短可知:PC>PD.
20.【解析】如图所示:C、D点即为所求.
21.【解析】(1)如图所示;根据图形可知B1(3,2),
故答案为:(3,2);
(2)如图所示:找C关于x轴的对称点C′,则C′(-2,-3),,
连接交x轴于一点M,根据两点之间线段最短,可知此时的M即为使周长最小时的点M.
22.【解析】画出图形如图所示,点P即为泵站的位置.
23.作点A关于直线a对称的点C,连接BC交a于点P,则点P就是抽水站的位置.
【解析】将在直线同侧的两个点分到直线的异侧,两点间线段最短
24.【解析】(1)如图所示,为所求作.
(2)由图可得,,,.
(3)如图所示,点即为所求作.
25.【解析】(1)如图所示,△A1B1C1即为所求;
(2)△A2B2C2可以由△A1B1C1向右平移6个单位,向下平移2个单位得到;
(3)如图,连接AB2,交x轴于P,连接A1P,则PA1+PB2最小,
此时,点P的坐标为(1,0).
答案第1页,总2页
答案第1页,总2页
