北师大版七上数学3.1字母表示数 课件(21张ppt)
文档属性
| 名称 | 北师大版七上数学3.1字母表示数 课件(21张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 965.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-16 00:00:00 | ||
图片预览




文档简介
3.1 字母表示数
数字游戏
随便想一个自然数,将这个数乘5减7,再把结果乘2加14.
无论你开始想的自然数是多少,只要你告诉我最终的计算结果,我就能猜出你想的自然数是几?你相信吗?不妨试试看!
2( 5 X – 7 )+ 14
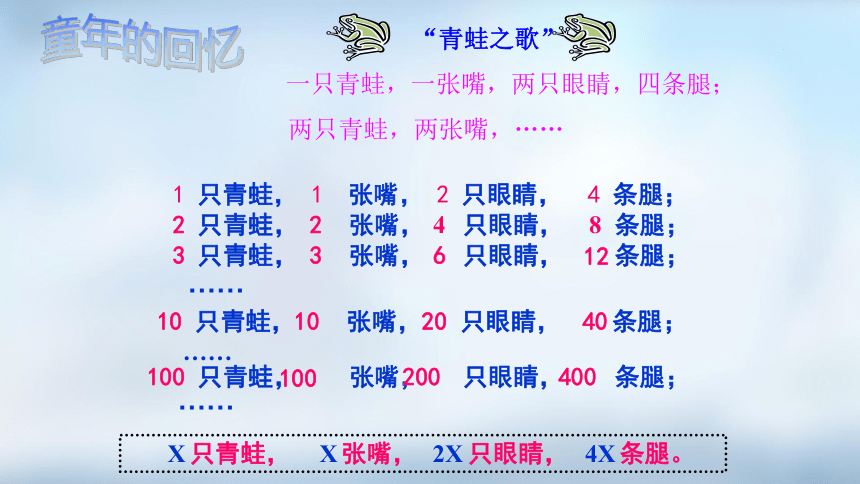
童年的回忆
1 只青蛙, 1 张嘴, 2 只眼睛, 4 条腿;
“青蛙之歌”
一只青蛙,一张嘴,两只眼睛,四条腿;
两只青蛙,两张嘴,……
2 只青蛙, 张嘴, 只眼睛, 条腿;
3 只青蛙, 张嘴, 只眼睛, 条腿;
……
10 只青蛙, 张嘴, 只眼睛, 条腿;
100 只青蛙, 张嘴, 只眼睛, 条腿;
只青蛙, 张嘴, 只眼睛, 条腿。
2
4
8
3
6
12
10
20
40
100
400
200
X
X
4X
2X
……
……
Index
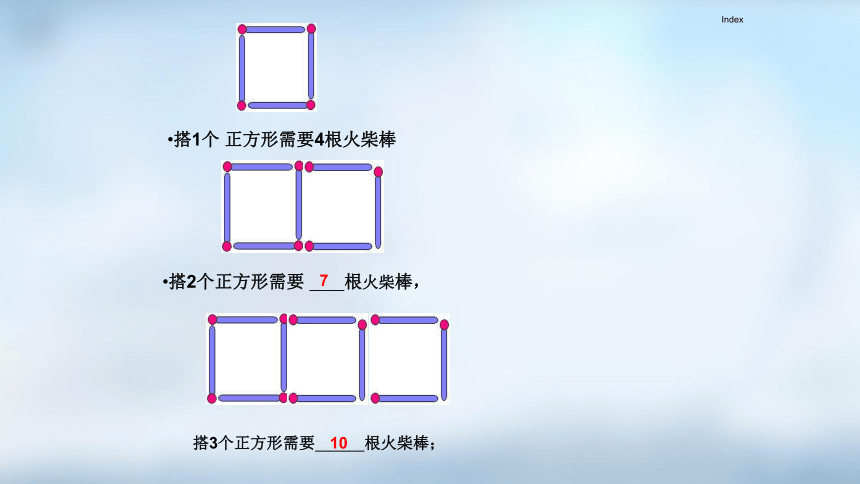
搭1个 正方形需要4根火柴棒
搭2个正方形需要 根火柴棒,
7
搭3个正方形需要 根火柴棒;
10
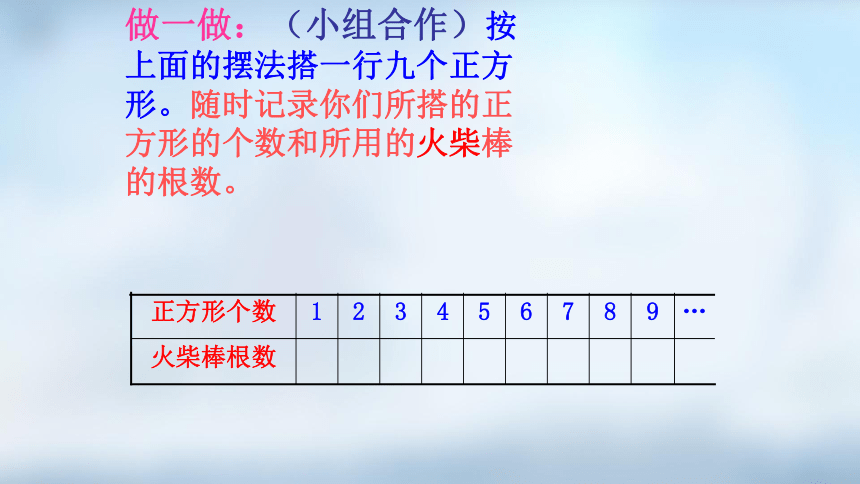
做一做:(小组合作)按上面的摆法搭一行九个正方形。随时记录你们所搭的正方形的个数和所用的火柴棒的根数。
火柴棒根数
…
9
8
7
6
5
4
3
2
1
正方形个数
…
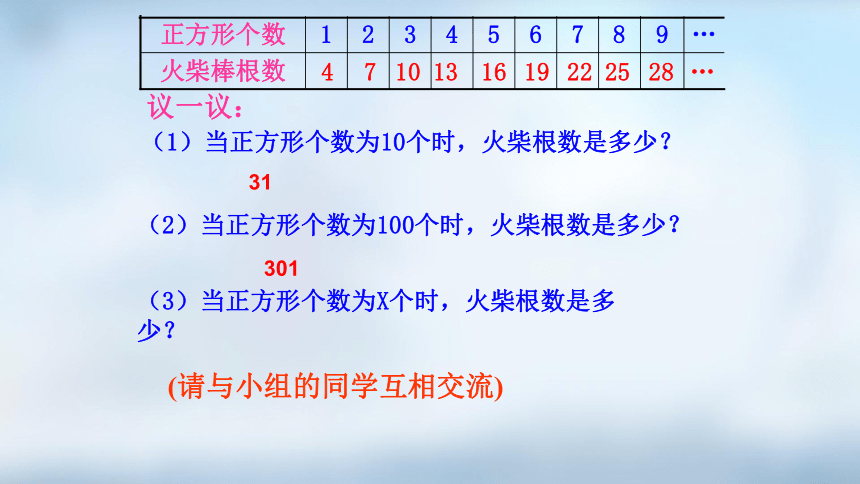
28
25
22
19
16
13
10
7
4
火柴棒根数
…
9
8
7
6
5
4
3
2
1
正方形个数
议一议:
(1)当正方形个数为10个时,火柴根数是多少?
(2)当正方形个数为100个时,火柴根数是多少?
(3)当正方形个数为X个时,火柴根数是多少?
(请与小组的同学互相交流)
31
301
方法1:以第一个搭的正方形为基础,然后每增加三根火柴棒,便多一个正方形。
…
…
…
正方形的个数
火柴根数
1
2
3
10
100
…
x
…
…
4
4+3
4+3+3
4+3+3+…+3
4+3+3+…+3
4+3+3+…+3
[即4+3(x-1)]
…
9个
99个
(x-1)个
方法2:
…
X个正方形
则共有:(1+3X)(根)
以第一根火柴为基础,然后每增加三根火柴棒,便多一个正方形。
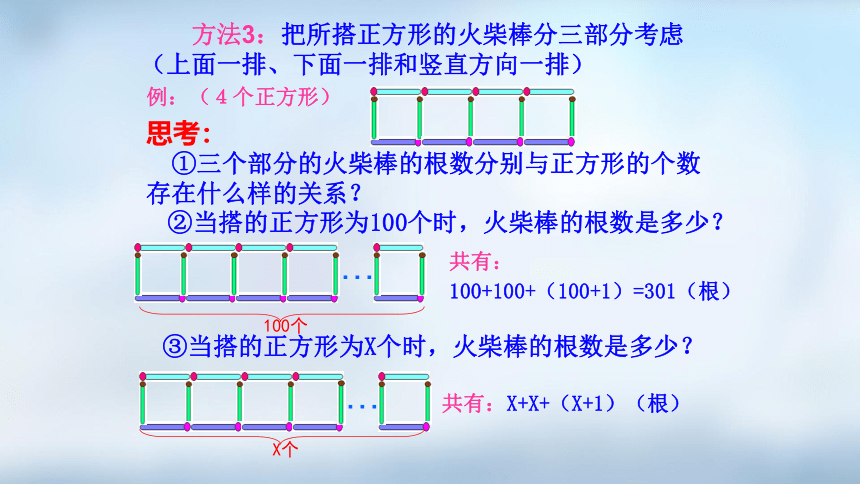
方法3:把所搭正方形的火柴棒分三部分考虑(上面一排、下面一排和竖直方向一排)
例:(4个正方形)
思考:
①三个部分的火柴棒的根数分别与正方形的个数存在什么样的关系?
②当搭的正方形为100个时,火柴棒的根数是多少?
…
100个
共有:
100+100+(100+1)=301(根)
③当搭的正方形为X个时,火柴棒的根数是多少?
X个
…
共有:X+X+(X+1)(根)
X个
搭x个正方形就需要[4x-(x-1)]根小棒
方法四:按照常规的方法搭一个正方形要4根火柴棒,重叠部分只要一根
由上我们知道,当用X来表示小正方形的个数时,火柴棒根数的计算方法有多种。
如:①4+3(X-1);
② 1 + 3 X;
③ X + X + ( X + 1 );
④4X – ( X – 1) 等等。
搭法不同公式不同
根据上面你的计算方法,要搭200个这样的正方形,需要多少根火柴棒呢?
利用方法1,我们用200代替4+3(X – 1)中的X,可以得到
4 + 3(200 – 1)= 601
4+3(x-1)
x+x+(x+1)
4x-(x-1)
1 + 3 X
字母能表示什么?
字母可表示任何数
(字母表示数在具体情形有具体意义)
你还能举出字母表示数 的其它例子吗?
问:
问:
1、运算律:
① 加法交换律:
a+b=b+a;
② 加法结合律:
(a+b)+c=a+(b+c);
③ 乘法交换律:
ab = ba;
④ 乘法结合律:
(ab)c=a(bc);
⑤ 分配率:
a(b+c)=ab+ac
字母可以表示任何数
2、用字母表示图形的周长、面积和体积。
4
3
长方形周长:
长方形面积:
(4 + 3)× 2
4 × 3
r
圆周长:
圆面积:
2πr
πr
2
a
b
c
长方体体积:
a b c
6
8
(8 + 6)× 2
8 × 6
m
n
2(m + n)
m n
长方体表面积:
2ab + 2bc + 2ac
字母能表示公式
练习一: 填空(口答)
1、每包书有12册,n包书有________册。
2、今年李华 m 岁,去年李华________ 岁,5年后李华________ 岁
3、温度由t℃下降2℃后是_______℃。
(t-2)
12n
4 、明明用 t 秒走了 s 米,他的速度为 ________米/秒
(m – 1 )
( m + 5 )
练习二: 填空
1、明明步行上学,速度为v米/秒;亮亮骑自行车上学,速度是明明的3倍,则亮亮的速度可以表示为_______米/秒。
2、如图,用字母表示图中阴影部分的面积为_________。
n
q
p
m
3v
mn-pq
2.字母表示数的意义
①给运算带来方便.
②可以把数或数量关系简明地表示出来.
小结:
3.在用字母表示数时,要注意以下几点:
①数与字母相乘或字母与字母相乘时,乘号“×”一般写成“·”,或省略不写,而且数字因数一般写在字母因数的前面。
②在同一问题中,不同意义的量要用不同字母表示
1、字母可以表示任何数;字母可以表示公式、法则、规律等。
本节课你的收获是什么?
数学作业
1.课本第79页 习题3.1
第1、2、3题(写在课本 不上交)
2.《全品》听课手册 作业手册
3.《优化设计》
课外拓展: 用火柴棒按下图的方式搭三角形
(1)填写下表:
三角形个数
1
2
3
4
5
火柴棒个数
(2)照这样的规律搭下去,搭n个这样的三角形需要多少根火柴棒?
3
5
7
9
11
3 + 2 ( n – 1 )
1 + 2 n
3 n - ( n – 1 )
试一试:用字母表示图中大正方形的面积,
你能用几种不同的方法表示?
“条条道路通罗马”
a
b
b
a
解:大正方形的面积为:
( a + b)
2
a + 2 a b + b
2
2
a ( a + b ) + b ( a + b )
做一做:若图中的 a = 1,b = 4,分别利用以上几
种方法求大正方形的面积,结果相等吗?
数字游戏
随便想一个自然数,将这个数乘5减7,再把结果乘2加14.
无论你开始想的自然数是多少,只要你告诉我最终的计算结果,我就能猜出你想的自然数是几?你相信吗?不妨试试看!
2( 5 X – 7 )+ 14
童年的回忆
1 只青蛙, 1 张嘴, 2 只眼睛, 4 条腿;
“青蛙之歌”
一只青蛙,一张嘴,两只眼睛,四条腿;
两只青蛙,两张嘴,……
2 只青蛙, 张嘴, 只眼睛, 条腿;
3 只青蛙, 张嘴, 只眼睛, 条腿;
……
10 只青蛙, 张嘴, 只眼睛, 条腿;
100 只青蛙, 张嘴, 只眼睛, 条腿;
只青蛙, 张嘴, 只眼睛, 条腿。
2
4
8
3
6
12
10
20
40
100
400
200
X
X
4X
2X
……
……
Index
搭1个 正方形需要4根火柴棒
搭2个正方形需要 根火柴棒,
7
搭3个正方形需要 根火柴棒;
10
做一做:(小组合作)按上面的摆法搭一行九个正方形。随时记录你们所搭的正方形的个数和所用的火柴棒的根数。
火柴棒根数
…
9
8
7
6
5
4
3
2
1
正方形个数
…
28
25
22
19
16
13
10
7
4
火柴棒根数
…
9
8
7
6
5
4
3
2
1
正方形个数
议一议:
(1)当正方形个数为10个时,火柴根数是多少?
(2)当正方形个数为100个时,火柴根数是多少?
(3)当正方形个数为X个时,火柴根数是多少?
(请与小组的同学互相交流)
31
301
方法1:以第一个搭的正方形为基础,然后每增加三根火柴棒,便多一个正方形。
…
…
…
正方形的个数
火柴根数
1
2
3
10
100
…
x
…
…
4
4+3
4+3+3
4+3+3+…+3
4+3+3+…+3
4+3+3+…+3
[即4+3(x-1)]
…
9个
99个
(x-1)个
方法2:
…
X个正方形
则共有:(1+3X)(根)
以第一根火柴为基础,然后每增加三根火柴棒,便多一个正方形。
方法3:把所搭正方形的火柴棒分三部分考虑(上面一排、下面一排和竖直方向一排)
例:(4个正方形)
思考:
①三个部分的火柴棒的根数分别与正方形的个数存在什么样的关系?
②当搭的正方形为100个时,火柴棒的根数是多少?
…
100个
共有:
100+100+(100+1)=301(根)
③当搭的正方形为X个时,火柴棒的根数是多少?
X个
…
共有:X+X+(X+1)(根)
X个
搭x个正方形就需要[4x-(x-1)]根小棒
方法四:按照常规的方法搭一个正方形要4根火柴棒,重叠部分只要一根
由上我们知道,当用X来表示小正方形的个数时,火柴棒根数的计算方法有多种。
如:①4+3(X-1);
② 1 + 3 X;
③ X + X + ( X + 1 );
④4X – ( X – 1) 等等。
搭法不同公式不同
根据上面你的计算方法,要搭200个这样的正方形,需要多少根火柴棒呢?
利用方法1,我们用200代替4+3(X – 1)中的X,可以得到
4 + 3(200 – 1)= 601
4+3(x-1)
x+x+(x+1)
4x-(x-1)
1 + 3 X
字母能表示什么?
字母可表示任何数
(字母表示数在具体情形有具体意义)
你还能举出字母表示数 的其它例子吗?
问:
问:
1、运算律:
① 加法交换律:
a+b=b+a;
② 加法结合律:
(a+b)+c=a+(b+c);
③ 乘法交换律:
ab = ba;
④ 乘法结合律:
(ab)c=a(bc);
⑤ 分配率:
a(b+c)=ab+ac
字母可以表示任何数
2、用字母表示图形的周长、面积和体积。
4
3
长方形周长:
长方形面积:
(4 + 3)× 2
4 × 3
r
圆周长:
圆面积:
2πr
πr
2
a
b
c
长方体体积:
a b c
6
8
(8 + 6)× 2
8 × 6
m
n
2(m + n)
m n
长方体表面积:
2ab + 2bc + 2ac
字母能表示公式
练习一: 填空(口答)
1、每包书有12册,n包书有________册。
2、今年李华 m 岁,去年李华________ 岁,5年后李华________ 岁
3、温度由t℃下降2℃后是_______℃。
(t-2)
12n
4 、明明用 t 秒走了 s 米,他的速度为 ________米/秒
(m – 1 )
( m + 5 )
练习二: 填空
1、明明步行上学,速度为v米/秒;亮亮骑自行车上学,速度是明明的3倍,则亮亮的速度可以表示为_______米/秒。
2、如图,用字母表示图中阴影部分的面积为_________。
n
q
p
m
3v
mn-pq
2.字母表示数的意义
①给运算带来方便.
②可以把数或数量关系简明地表示出来.
小结:
3.在用字母表示数时,要注意以下几点:
①数与字母相乘或字母与字母相乘时,乘号“×”一般写成“·”,或省略不写,而且数字因数一般写在字母因数的前面。
②在同一问题中,不同意义的量要用不同字母表示
1、字母可以表示任何数;字母可以表示公式、法则、规律等。
本节课你的收获是什么?
数学作业
1.课本第79页 习题3.1
第1、2、3题(写在课本 不上交)
2.《全品》听课手册 作业手册
3.《优化设计》
课外拓展: 用火柴棒按下图的方式搭三角形
(1)填写下表:
三角形个数
1
2
3
4
5
火柴棒个数
(2)照这样的规律搭下去,搭n个这样的三角形需要多少根火柴棒?
3
5
7
9
11
3 + 2 ( n – 1 )
1 + 2 n
3 n - ( n – 1 )
试一试:用字母表示图中大正方形的面积,
你能用几种不同的方法表示?
“条条道路通罗马”
a
b
b
a
解:大正方形的面积为:
( a + b)
2
a + 2 a b + b
2
2
a ( a + b ) + b ( a + b )
做一做:若图中的 a = 1,b = 4,分别利用以上几
种方法求大正方形的面积,结果相等吗?
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
