2021-2022学年沪科新版八年级上册数学《第11章 平面直角坐标系》单元测试卷(word版含解析)
文档属性
| 名称 | 2021-2022学年沪科新版八年级上册数学《第11章 平面直角坐标系》单元测试卷(word版含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 226.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-16 00:00:00 | ||
图片预览



文档简介
2021-2022学年沪科新版八年级上册数学《第11章
平面直角坐标系》单元测试卷
一.选择题
1.在平面直角坐标系中,点A(2,﹣3)所在的象限是( )
A.第一象限
B.第二象限
C.第三象限
D.第四象限
2.已知点P(x,y)的坐标满足|x|=3,=2,且xy<0,则点P的坐标是( )
A.(3,﹣2)
B.(﹣3,2)
C.(3,﹣4)
D.(﹣3,4)
3.如图,若在中国象棋盘上建立平面直角坐标系,使“帅”位于点(﹣1,﹣1),“马”位于点(2,﹣1),则“兵”位于点( )
A.(﹣1,2)
B.(﹣3,2)
C.(﹣3,1)
D.(﹣2,3)
4.如果点P(m,1﹣2m)在第一象限,那么m的取值范围是( )
A.0<m<
B.﹣<m<0
C.m<0
D.m>
5.如图,若在中国象棋盘上建立平面直角坐标系,使“帅”位于点(﹣1,﹣2),“马”位于点(2,﹣2),则“兵”位于点( )
A.(﹣1,1)
B.(﹣2,﹣1)
C.(﹣3,1)
D.(1,﹣2)
6.在平面直角坐标系中,点P(0,﹣4)在( )
A.x轴上
B.y轴上
C.原点
D.与x轴平行的直线上
7.平面直角坐标系中,将点A(﹣3,﹣5)向上平移4个单位,再向左平移3个单位到点B,则点B的坐标为( )
A.(1,﹣8)
B.(1,﹣2)
C.(﹣6,﹣1)
D.(0,﹣1)
8.如图,雷达探测器测得六个目标A,B,C,D,E,F出现按照规定的目标表示方法,目标E,F的位置表示为E(3,300°),F(5,210°),按照此方法在表示目标A,B,C,D的位置时,其中表示不正确的是( )
A.A(4,30°)
B.B(2,90°)
C.C(6,120°)
D.D(3,240°)
9.在平面直角坐标系中,在第三象限的点是( )
A.(﹣3,5)
B.(1,﹣2)
C.(﹣2,﹣3)
D.(1,1)
10.如图,在平面直角坐标系中,线段AB的两个端点是A(1,3),B(2,1).将线段AB沿某一方向平移后,若点A的对应点A′的坐标为(﹣2,0),则点B的对应点B′的坐标为( )
A.(﹣3,2)
B.(﹣1,﹣3)
C.(﹣1,﹣2)
D.(0,﹣2)
二.填空题
11.若点A的坐标是(﹣3,5),则它到x轴的距离是
.
12.点M(﹣2,3)到x轴的距离是
.
13.若点P(2x﹣2,﹣x+4)到两坐标轴的距离相等,则点P的坐标为
.
14.在平面直角坐标系中,如果一个点的横、纵坐标均为整数,那么我们称该点是格点.若格点P(2m﹣1,m+2)在第二象限,则m的值为
.
15.如图,已知棋子“车”的坐标为(﹣2,3),棋子“马”的坐标为(1,3),则棋子“炮”的坐标为
.
16.在平面直角坐标系中,若点M(1,x)与点N(1,3)之间的距离是5,则x的值是
.
17.在平面直角坐标系内,把点P(﹣5,﹣2)先向左平移2个单位长度,再向上平移4个单位长度后得到的点的坐标是
.
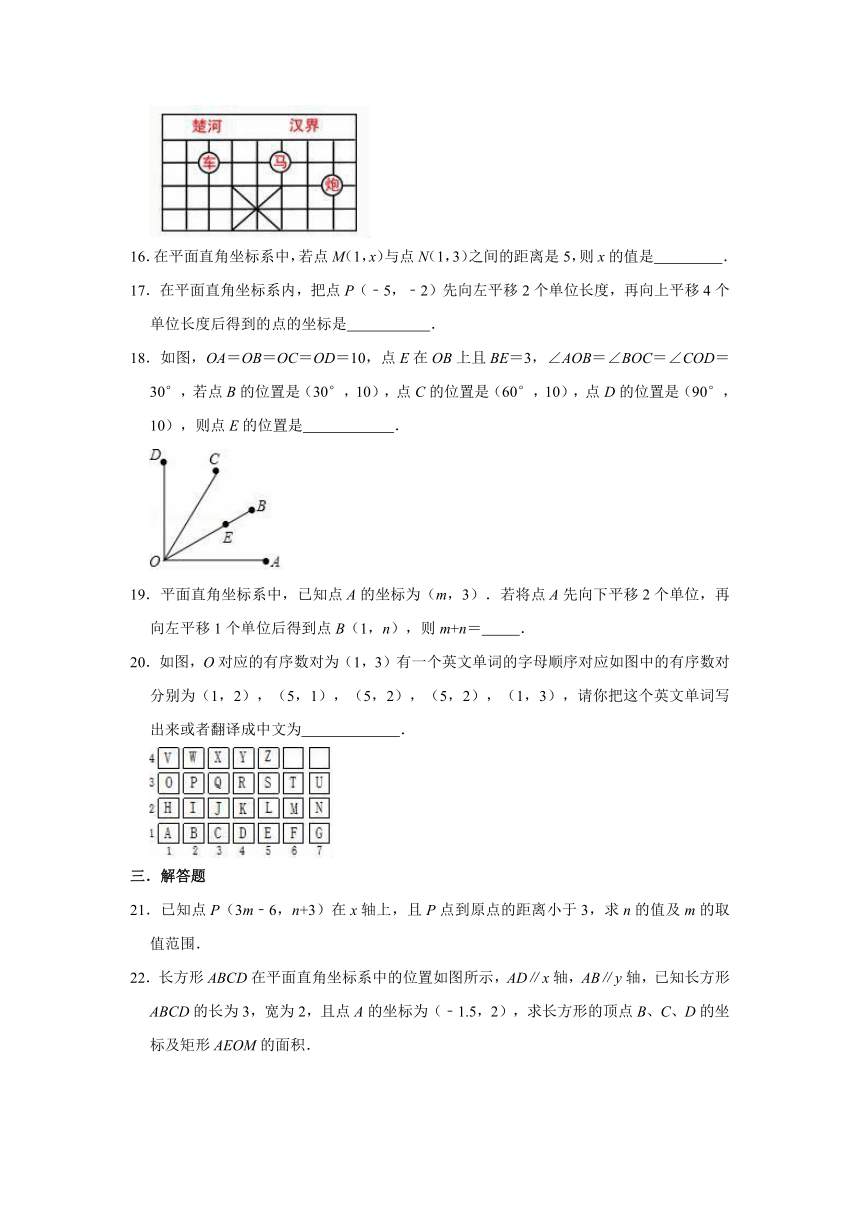
18.如图,OA=OB=OC=OD=10,点E在OB上且BE=3,∠AOB=∠BOC=∠COD=30°,若点B的位置是(30°,10),点C的位置是(60°,10),点D的位置是(90°,10),则点E的位置是
.
19.平面直角坐标系中,已知点A的坐标为(m,3).若将点A先向下平移2个单位,再向左平移1个单位后得到点B(1,n),则m+n=
.
20.如图,O对应的有序数对为(1,3)有一个英文单词的字母顺序对应如图中的有序数对分别为(1,2),(5,1),(5,2),(5,2),(1,3),请你把这个英文单词写出来或者翻译成中文为
.
三.解答题
21.已知点P(3m﹣6,n+3)在x轴上,且P点到原点的距离小于3,求n的值及m的取值范围.
22.长方形ABCD在平面直角坐标系中的位置如图所示,AD∥x轴,AB∥y轴,已知长方形ABCD的长为3,宽为2,且点A的坐标为(﹣1.5,2),求长方形的顶点B、C、D的坐标及矩形AEOM的面积.
23.已知点P(a﹣2,2a+8),分别根据下列条件求出点P的坐标.
(1)点P在x轴上;
(2)点P在y轴上;
(3)点Q的坐标为(1,5),直线PQ∥y轴;
(4)点P到x轴、y轴的距离相等.
24.在平面直角坐标系xOy中,对于点P(x,y),若点Q的坐标为(ax+y,x+ay),其中a为常数,则称点Q是点P的“a级关联点”例如,点P(1,4)的“3级关联点”为Q(3×1+4,1+3×4),即Q(7,13).
(1)已知点A(﹣2,6)的“级关联点”是点A1,求点A1的坐标.
(2)已知点M(m﹣1,2m)的“﹣3级关联点”M′位于y轴上.求点M′的坐标.
25.如图所示,A(1,0)、点B在y轴上,将三角形OAB沿x轴负方向平移,平移后的图形为三角形DEC,且点C的坐标为(a,b),且a=+﹣3.
(1)直接写出点C的坐标
;
(2)直接写出点E的坐标
;
(3)点P是CE上一动点,设∠CBP=x°,∠PAD=y°,∠BPA=z°,确定x,y,z之间的数量关系,并证明你的结论.
26.如图,P(x0,y0)为△ABC内任意一点,若将△ABC作平移变换,使A点落在B点的位置上,已知A(3,4);B(﹣2,2);C(2,﹣2).
(1)请直接写出B点、C点、P点的对应点B1、C1、P1的坐标;
(2)求S△AOC.
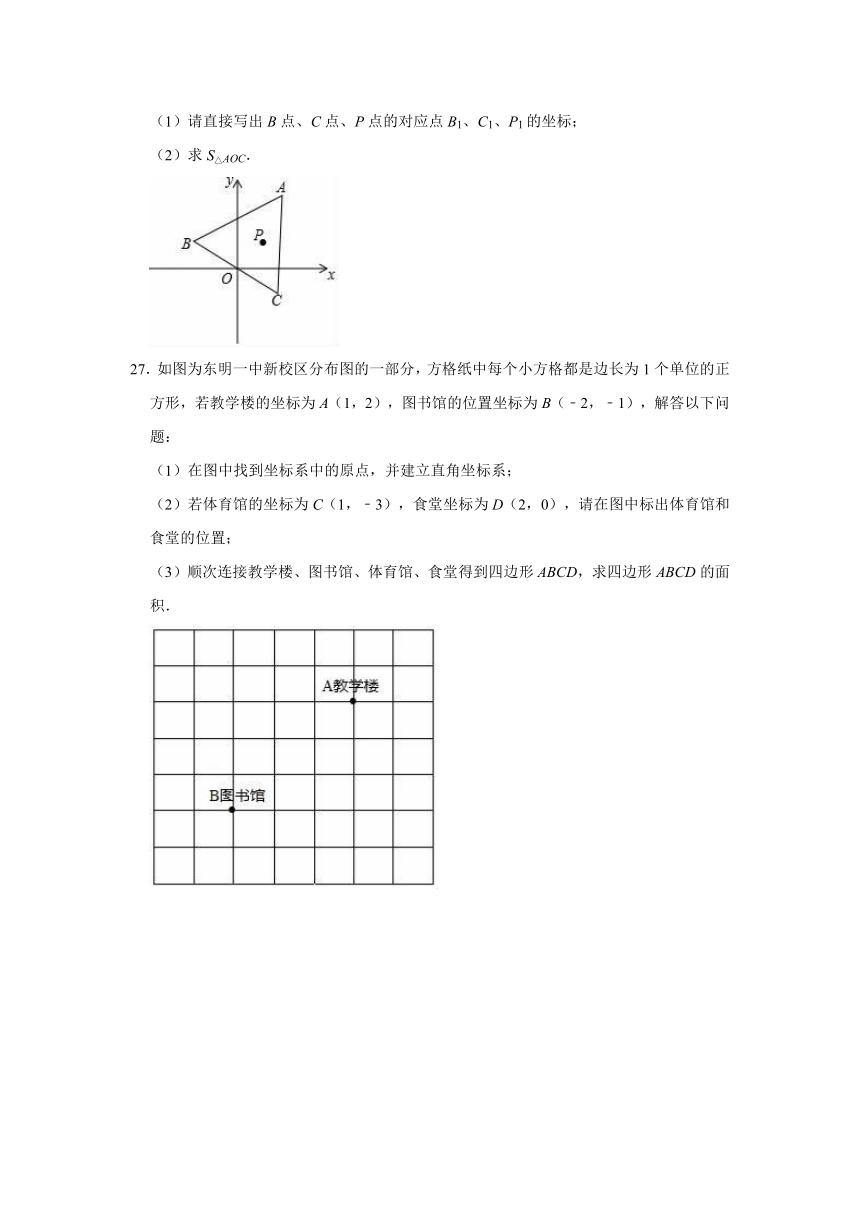
27.如图为东明一中新校区分布图的一部分,方格纸中每个小方格都是边长为1个单位的正方形,若教学楼的坐标为A(1,2),图书馆的位置坐标为B(﹣2,﹣1),解答以下问题:
(1)在图中找到坐标系中的原点,并建立直角坐标系;
(2)若体育馆的坐标为C(1,﹣3),食堂坐标为D(2,0),请在图中标出体育馆和食堂的位置;
(3)顺次连接教学楼、图书馆、体育馆、食堂得到四边形ABCD,求四边形ABCD的面积.
参考答案与试题解析
一.选择题
1.解:点A(2,﹣3)所在的象限是第四象限.
故选:D.
2.解:∵|x|=3,=2,
∴x=3或﹣3,y=4,
∵xy<0,
∴x=﹣3,y=4,
∴点P的坐标为(﹣3,4),
故选:D.
3.解:如图所示:则“兵”位于(﹣3,2).
故选:B.
4.解:∵点P(m,1﹣2m)在第一象限,
∴,
由②得,m<,
所以,m的取值范围是0<m<.
故选:A.
5.解:如图,
“兵”位于点(﹣3,1).
故选:C.
6.解:在平面直角坐标系中,点P(0,﹣4)在y轴上,
故选:B.
7.解:点A的坐标为(﹣3,﹣5),将点A向上平移4个单位,再向左平移3个单位到点B,
点B的横坐标是﹣3﹣3=﹣6,纵坐标为﹣5+4=﹣1,即(﹣6,﹣1).
故选:C.
8.解:因为E(3,300°),F(5,210°),
可得:A(4,30°),B(2,90°),C(6,120°),D(4,240°),
故选:D.
9.解:A、(﹣3,5)在第二象限,不符合题意;
B、(1,﹣2)在第四象限,不符合题意;
C、(﹣2,﹣3)在第三象限,符合题意;
D、(1,1)在第一象限,不符合题意,
故选:C.
10.解:观察图象可知,点B的对应点B′的坐标为(﹣1,﹣2).
故选:C.
二.填空题
11.解:根据点的坐标(﹣3,5),
可得它到x轴的距离是|5|=5;
故答案为5.故填5.
12.解:M(﹣2,3)到x轴的距离是其纵坐标的绝对值,即为3.
故答案为3.
13.解:∵点P到两轴的距离相等,
∴2x﹣2=﹣x+4或2x﹣2=﹣(﹣x+4),
即x=2或x=﹣2,
代入点P坐标(2,2)或(﹣6,6).
故答案为:(2,2)或(﹣6,6).
14.解:∵格点P(2m﹣1,m+2)在第二象限,
∴,
解不等式①得,m<,
解不等式②得,m>﹣2,
∴不等式的解集为﹣2<m<,
∵点的横、纵坐标均为整数,
∴m是整数,
∴m的值为﹣1或0.
故答案为:﹣1或0.
15.解:∵棋子“车”的坐标为(﹣2,3),棋子“马”的坐标为(1,3)
∴坐标系的原点为O,如图所示,
∴棋子“炮”的坐标为(3,2).故答案填:(3,2).
16.解:∵点M(1,x)与点N(1,3)之间的距离是5,
∴|x﹣3|=5,
解得x=﹣2或8.
故答案为:﹣2或8.
17.解:原来点的横坐标是﹣5,纵坐标是﹣2,向左平移2个单位长度,再向上平移4个单位得到新点的横坐标是﹣5﹣2=﹣7,纵坐标为﹣2+4=2.
得到的点的坐标是(﹣7,2).
故答案为:(﹣7,2).
18.解:∵BO=10,BE=3,
∴OE=7,
∵∠AOB=30°,
∴点E的位置是:(30°,7).
故答案是:(30°,7).
19.解:∵点A(m,3)向下平移2个单位,向左平移1个单位后得到点B(1,n),
∴m﹣1=1,3﹣2=n,
∴m=2,n=1,
∴m+n=3,
故答案为:3.
20.解:H(1,2),E(5,1),L(5,2),L(5,2),O(1,3),
所以,这个单词为HELLO.
故答案为:HELLO或你好.
三.解答题
21.解:∵点P(3m﹣6,n+3)在x轴上,
∴n+3=0,
∴n=﹣3,
∵P点到原点的距离小于3,
∴|3m﹣6|<3,
∴﹣3<3m﹣6<3,
∴m的取值范围是1<m<3.
22.解:∵AD∥x轴,AB∥y轴,点A的坐标为(﹣1.5,2),
∴AM=1.5,AE=2,
∵长方形ABCD的长为3,宽为2,
∴AB=CD=3,AD=BC=2,
∴BE=CF=1,MD=CN=0.5,
∴B点坐标为(﹣1.5,﹣1),C点坐标为(0.5,﹣1),D点坐标为(0.5,2);
故矩形AEOM的面积=1.5×2=3.
23.解:(1)∵点P(a﹣2,2a+8),在x轴上,
∴2a+8=0,
解得:a=﹣4,
故a﹣2=﹣4﹣2=﹣6,
则P(﹣6,0);
(2))∵点P(a﹣2,2a+8),在y轴上,
∴a﹣2=0,
解得:a=2,
故2a+8=2×2+8=12,
则P(0,12);
(3)∵点Q的坐标为(1,5),直线PQ∥y轴;,
∴a﹣2=1,
解得:a=3,
故2a+8=14,
则P(1,14);
(4)∵点P到x轴、y轴的距离相等,
∴a﹣2=2a+8或a﹣2+2a+8=0,
解得:a1=﹣10,a2=﹣2,
故当a=﹣10则:a﹣2=﹣12,2a+8=﹣12,
则P(﹣12,﹣12);
故当a=﹣2则:a﹣2=﹣4,2a+8=4,
则P(﹣4,4).
综上所述:P(﹣12,﹣12),(﹣4,4).
24.解(1)因为点A(﹣2,6)的“级关联点”是点A1,所以A1为A1(5,1).
(2)∵点M(m﹣1,2m)的“﹣3级关联点”为M′(﹣3(m﹣1)+2m,m﹣1+(﹣3)×2m),M′位于y轴上,
∴﹣3(m﹣1)+2m=0,
解得:m=3
∴m﹣1+(﹣3)×2m=﹣16,
∴M′(0,﹣16).
25.解:(1)∵a=+﹣3,
∴b=2,a=﹣3,
∵点C的坐标为(a,b),
∴点C的坐标为:(﹣3,2);
故答案为:(﹣3,2);
(2)∵点B在y轴上,点C的坐标为:(﹣3,2),
∴B点向左平移了3个单位长度,
∴A(1,0),向左平移3个单位得到:(﹣2,0)
∴点E的坐标为:(﹣2,0);
故答案为:(﹣2,0);
(3)x+y=z.证明如下:
如图,过点P作PN∥CB,
∴∠CBP=∠BPN
又∵BC∥AE,
∴PN∥AE
∴∠EAP=∠APN
∴∠CBP+∠EAP=∠BPN+∠APN=∠APB,
即x+y=z.
26.解:(1)由点A(3,4)平移后的对应点的坐标为(﹣2,2),
所以需将△ABC向左平移5个单位、向下平移2个单位,
则点B(﹣2,2)的对应点B1的坐标为(﹣7,0),
点C(2,﹣2)的对应点C1的坐标为(﹣3,﹣4),
点P(x0,y0)的对应点P1的坐标为(x0﹣5,y0﹣2);
(2)如图所示,过点A作AD⊥y轴于点D,过点C作CE⊥y轴,
则AD=3、CE=2、OD=4、OE=2,
∴S△AOC=×(2+3)×6﹣×3×4﹣×2×2
=15﹣6﹣2
=7.
27.解:(1)建立平面直角坐标系如图所示;
(2)体育馆C(1,﹣3),食堂D(2,0)如图所示;
(3)四边形ABCD的面积=4×5﹣×3×3﹣×2×3﹣×1×3﹣×1×2,
=20﹣4.5﹣3﹣1.5﹣1,
=20﹣10,
=10.
平面直角坐标系》单元测试卷
一.选择题
1.在平面直角坐标系中,点A(2,﹣3)所在的象限是( )
A.第一象限
B.第二象限
C.第三象限
D.第四象限
2.已知点P(x,y)的坐标满足|x|=3,=2,且xy<0,则点P的坐标是( )
A.(3,﹣2)
B.(﹣3,2)
C.(3,﹣4)
D.(﹣3,4)
3.如图,若在中国象棋盘上建立平面直角坐标系,使“帅”位于点(﹣1,﹣1),“马”位于点(2,﹣1),则“兵”位于点( )
A.(﹣1,2)
B.(﹣3,2)
C.(﹣3,1)
D.(﹣2,3)
4.如果点P(m,1﹣2m)在第一象限,那么m的取值范围是( )
A.0<m<
B.﹣<m<0
C.m<0
D.m>
5.如图,若在中国象棋盘上建立平面直角坐标系,使“帅”位于点(﹣1,﹣2),“马”位于点(2,﹣2),则“兵”位于点( )
A.(﹣1,1)
B.(﹣2,﹣1)
C.(﹣3,1)
D.(1,﹣2)
6.在平面直角坐标系中,点P(0,﹣4)在( )
A.x轴上
B.y轴上
C.原点
D.与x轴平行的直线上
7.平面直角坐标系中,将点A(﹣3,﹣5)向上平移4个单位,再向左平移3个单位到点B,则点B的坐标为( )
A.(1,﹣8)
B.(1,﹣2)
C.(﹣6,﹣1)
D.(0,﹣1)
8.如图,雷达探测器测得六个目标A,B,C,D,E,F出现按照规定的目标表示方法,目标E,F的位置表示为E(3,300°),F(5,210°),按照此方法在表示目标A,B,C,D的位置时,其中表示不正确的是( )
A.A(4,30°)
B.B(2,90°)
C.C(6,120°)
D.D(3,240°)
9.在平面直角坐标系中,在第三象限的点是( )
A.(﹣3,5)
B.(1,﹣2)
C.(﹣2,﹣3)
D.(1,1)
10.如图,在平面直角坐标系中,线段AB的两个端点是A(1,3),B(2,1).将线段AB沿某一方向平移后,若点A的对应点A′的坐标为(﹣2,0),则点B的对应点B′的坐标为( )
A.(﹣3,2)
B.(﹣1,﹣3)
C.(﹣1,﹣2)
D.(0,﹣2)
二.填空题
11.若点A的坐标是(﹣3,5),则它到x轴的距离是
.
12.点M(﹣2,3)到x轴的距离是
.
13.若点P(2x﹣2,﹣x+4)到两坐标轴的距离相等,则点P的坐标为
.
14.在平面直角坐标系中,如果一个点的横、纵坐标均为整数,那么我们称该点是格点.若格点P(2m﹣1,m+2)在第二象限,则m的值为
.
15.如图,已知棋子“车”的坐标为(﹣2,3),棋子“马”的坐标为(1,3),则棋子“炮”的坐标为
.
16.在平面直角坐标系中,若点M(1,x)与点N(1,3)之间的距离是5,则x的值是
.
17.在平面直角坐标系内,把点P(﹣5,﹣2)先向左平移2个单位长度,再向上平移4个单位长度后得到的点的坐标是
.
18.如图,OA=OB=OC=OD=10,点E在OB上且BE=3,∠AOB=∠BOC=∠COD=30°,若点B的位置是(30°,10),点C的位置是(60°,10),点D的位置是(90°,10),则点E的位置是
.
19.平面直角坐标系中,已知点A的坐标为(m,3).若将点A先向下平移2个单位,再向左平移1个单位后得到点B(1,n),则m+n=
.
20.如图,O对应的有序数对为(1,3)有一个英文单词的字母顺序对应如图中的有序数对分别为(1,2),(5,1),(5,2),(5,2),(1,3),请你把这个英文单词写出来或者翻译成中文为
.
三.解答题
21.已知点P(3m﹣6,n+3)在x轴上,且P点到原点的距离小于3,求n的值及m的取值范围.
22.长方形ABCD在平面直角坐标系中的位置如图所示,AD∥x轴,AB∥y轴,已知长方形ABCD的长为3,宽为2,且点A的坐标为(﹣1.5,2),求长方形的顶点B、C、D的坐标及矩形AEOM的面积.
23.已知点P(a﹣2,2a+8),分别根据下列条件求出点P的坐标.
(1)点P在x轴上;
(2)点P在y轴上;
(3)点Q的坐标为(1,5),直线PQ∥y轴;
(4)点P到x轴、y轴的距离相等.
24.在平面直角坐标系xOy中,对于点P(x,y),若点Q的坐标为(ax+y,x+ay),其中a为常数,则称点Q是点P的“a级关联点”例如,点P(1,4)的“3级关联点”为Q(3×1+4,1+3×4),即Q(7,13).
(1)已知点A(﹣2,6)的“级关联点”是点A1,求点A1的坐标.
(2)已知点M(m﹣1,2m)的“﹣3级关联点”M′位于y轴上.求点M′的坐标.
25.如图所示,A(1,0)、点B在y轴上,将三角形OAB沿x轴负方向平移,平移后的图形为三角形DEC,且点C的坐标为(a,b),且a=+﹣3.
(1)直接写出点C的坐标
;
(2)直接写出点E的坐标
;
(3)点P是CE上一动点,设∠CBP=x°,∠PAD=y°,∠BPA=z°,确定x,y,z之间的数量关系,并证明你的结论.
26.如图,P(x0,y0)为△ABC内任意一点,若将△ABC作平移变换,使A点落在B点的位置上,已知A(3,4);B(﹣2,2);C(2,﹣2).
(1)请直接写出B点、C点、P点的对应点B1、C1、P1的坐标;
(2)求S△AOC.
27.如图为东明一中新校区分布图的一部分,方格纸中每个小方格都是边长为1个单位的正方形,若教学楼的坐标为A(1,2),图书馆的位置坐标为B(﹣2,﹣1),解答以下问题:
(1)在图中找到坐标系中的原点,并建立直角坐标系;
(2)若体育馆的坐标为C(1,﹣3),食堂坐标为D(2,0),请在图中标出体育馆和食堂的位置;
(3)顺次连接教学楼、图书馆、体育馆、食堂得到四边形ABCD,求四边形ABCD的面积.
参考答案与试题解析
一.选择题
1.解:点A(2,﹣3)所在的象限是第四象限.
故选:D.
2.解:∵|x|=3,=2,
∴x=3或﹣3,y=4,
∵xy<0,
∴x=﹣3,y=4,
∴点P的坐标为(﹣3,4),
故选:D.
3.解:如图所示:则“兵”位于(﹣3,2).
故选:B.
4.解:∵点P(m,1﹣2m)在第一象限,
∴,
由②得,m<,
所以,m的取值范围是0<m<.
故选:A.
5.解:如图,
“兵”位于点(﹣3,1).
故选:C.
6.解:在平面直角坐标系中,点P(0,﹣4)在y轴上,
故选:B.
7.解:点A的坐标为(﹣3,﹣5),将点A向上平移4个单位,再向左平移3个单位到点B,
点B的横坐标是﹣3﹣3=﹣6,纵坐标为﹣5+4=﹣1,即(﹣6,﹣1).
故选:C.
8.解:因为E(3,300°),F(5,210°),
可得:A(4,30°),B(2,90°),C(6,120°),D(4,240°),
故选:D.
9.解:A、(﹣3,5)在第二象限,不符合题意;
B、(1,﹣2)在第四象限,不符合题意;
C、(﹣2,﹣3)在第三象限,符合题意;
D、(1,1)在第一象限,不符合题意,
故选:C.
10.解:观察图象可知,点B的对应点B′的坐标为(﹣1,﹣2).
故选:C.
二.填空题
11.解:根据点的坐标(﹣3,5),
可得它到x轴的距离是|5|=5;
故答案为5.故填5.
12.解:M(﹣2,3)到x轴的距离是其纵坐标的绝对值,即为3.
故答案为3.
13.解:∵点P到两轴的距离相等,
∴2x﹣2=﹣x+4或2x﹣2=﹣(﹣x+4),
即x=2或x=﹣2,
代入点P坐标(2,2)或(﹣6,6).
故答案为:(2,2)或(﹣6,6).
14.解:∵格点P(2m﹣1,m+2)在第二象限,
∴,
解不等式①得,m<,
解不等式②得,m>﹣2,
∴不等式的解集为﹣2<m<,
∵点的横、纵坐标均为整数,
∴m是整数,
∴m的值为﹣1或0.
故答案为:﹣1或0.
15.解:∵棋子“车”的坐标为(﹣2,3),棋子“马”的坐标为(1,3)
∴坐标系的原点为O,如图所示,
∴棋子“炮”的坐标为(3,2).故答案填:(3,2).
16.解:∵点M(1,x)与点N(1,3)之间的距离是5,
∴|x﹣3|=5,
解得x=﹣2或8.
故答案为:﹣2或8.
17.解:原来点的横坐标是﹣5,纵坐标是﹣2,向左平移2个单位长度,再向上平移4个单位得到新点的横坐标是﹣5﹣2=﹣7,纵坐标为﹣2+4=2.
得到的点的坐标是(﹣7,2).
故答案为:(﹣7,2).
18.解:∵BO=10,BE=3,
∴OE=7,
∵∠AOB=30°,
∴点E的位置是:(30°,7).
故答案是:(30°,7).
19.解:∵点A(m,3)向下平移2个单位,向左平移1个单位后得到点B(1,n),
∴m﹣1=1,3﹣2=n,
∴m=2,n=1,
∴m+n=3,
故答案为:3.
20.解:H(1,2),E(5,1),L(5,2),L(5,2),O(1,3),
所以,这个单词为HELLO.
故答案为:HELLO或你好.
三.解答题
21.解:∵点P(3m﹣6,n+3)在x轴上,
∴n+3=0,
∴n=﹣3,
∵P点到原点的距离小于3,
∴|3m﹣6|<3,
∴﹣3<3m﹣6<3,
∴m的取值范围是1<m<3.
22.解:∵AD∥x轴,AB∥y轴,点A的坐标为(﹣1.5,2),
∴AM=1.5,AE=2,
∵长方形ABCD的长为3,宽为2,
∴AB=CD=3,AD=BC=2,
∴BE=CF=1,MD=CN=0.5,
∴B点坐标为(﹣1.5,﹣1),C点坐标为(0.5,﹣1),D点坐标为(0.5,2);
故矩形AEOM的面积=1.5×2=3.
23.解:(1)∵点P(a﹣2,2a+8),在x轴上,
∴2a+8=0,
解得:a=﹣4,
故a﹣2=﹣4﹣2=﹣6,
则P(﹣6,0);
(2))∵点P(a﹣2,2a+8),在y轴上,
∴a﹣2=0,
解得:a=2,
故2a+8=2×2+8=12,
则P(0,12);
(3)∵点Q的坐标为(1,5),直线PQ∥y轴;,
∴a﹣2=1,
解得:a=3,
故2a+8=14,
则P(1,14);
(4)∵点P到x轴、y轴的距离相等,
∴a﹣2=2a+8或a﹣2+2a+8=0,
解得:a1=﹣10,a2=﹣2,
故当a=﹣10则:a﹣2=﹣12,2a+8=﹣12,
则P(﹣12,﹣12);
故当a=﹣2则:a﹣2=﹣4,2a+8=4,
则P(﹣4,4).
综上所述:P(﹣12,﹣12),(﹣4,4).
24.解(1)因为点A(﹣2,6)的“级关联点”是点A1,所以A1为A1(5,1).
(2)∵点M(m﹣1,2m)的“﹣3级关联点”为M′(﹣3(m﹣1)+2m,m﹣1+(﹣3)×2m),M′位于y轴上,
∴﹣3(m﹣1)+2m=0,
解得:m=3
∴m﹣1+(﹣3)×2m=﹣16,
∴M′(0,﹣16).
25.解:(1)∵a=+﹣3,
∴b=2,a=﹣3,
∵点C的坐标为(a,b),
∴点C的坐标为:(﹣3,2);
故答案为:(﹣3,2);
(2)∵点B在y轴上,点C的坐标为:(﹣3,2),
∴B点向左平移了3个单位长度,
∴A(1,0),向左平移3个单位得到:(﹣2,0)
∴点E的坐标为:(﹣2,0);
故答案为:(﹣2,0);
(3)x+y=z.证明如下:
如图,过点P作PN∥CB,
∴∠CBP=∠BPN
又∵BC∥AE,
∴PN∥AE
∴∠EAP=∠APN
∴∠CBP+∠EAP=∠BPN+∠APN=∠APB,
即x+y=z.
26.解:(1)由点A(3,4)平移后的对应点的坐标为(﹣2,2),
所以需将△ABC向左平移5个单位、向下平移2个单位,
则点B(﹣2,2)的对应点B1的坐标为(﹣7,0),
点C(2,﹣2)的对应点C1的坐标为(﹣3,﹣4),
点P(x0,y0)的对应点P1的坐标为(x0﹣5,y0﹣2);
(2)如图所示,过点A作AD⊥y轴于点D,过点C作CE⊥y轴,
则AD=3、CE=2、OD=4、OE=2,
∴S△AOC=×(2+3)×6﹣×3×4﹣×2×2
=15﹣6﹣2
=7.
27.解:(1)建立平面直角坐标系如图所示;
(2)体育馆C(1,﹣3),食堂D(2,0)如图所示;
(3)四边形ABCD的面积=4×5﹣×3×3﹣×2×3﹣×1×3﹣×1×2,
=20﹣4.5﹣3﹣1.5﹣1,
=20﹣10,
=10.
