2021-2022学年沪科新版九年级上册数学《第21章 二次函数与反比例函数》单元测试卷(word版含解析)
文档属性
| 名称 | 2021-2022学年沪科新版九年级上册数学《第21章 二次函数与反比例函数》单元测试卷(word版含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 219.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-16 13:35:12 | ||
图片预览

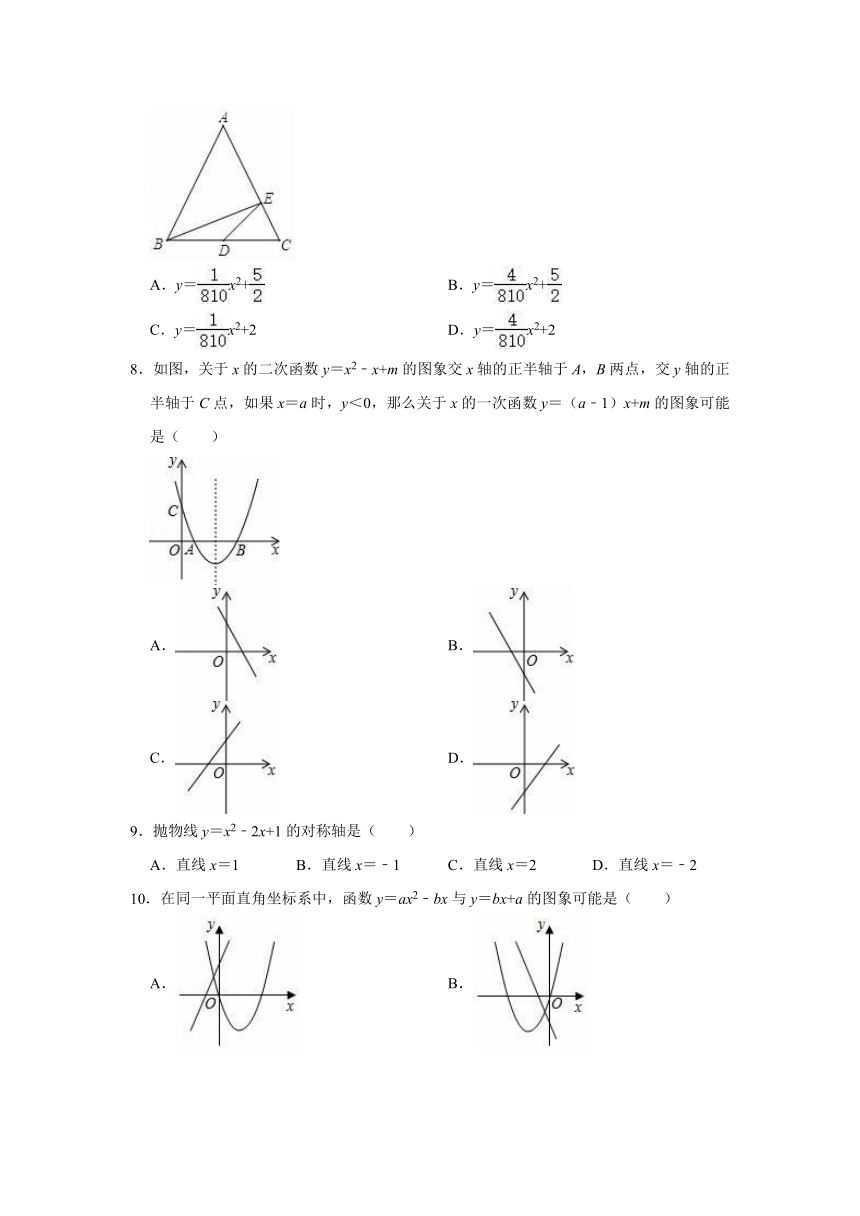


文档简介
2021-2022学年沪科新版九年级上册数学《第21章
二次函数与反比例函数》单元测试卷
一.选择题
1.下列函数不是反比例函数的是( )
A.y=3x﹣1
B.y=﹣
C.xy=5
D.y=
2.下列函数中y是x的二次函数的是( )
A.y=(x+1)(2x﹣1)﹣2x2
B.y=﹣2x+1
C.y=3x2﹣x+5
D.y=ax2+bx+c
3.在下列4个不同的情境中,两个变量所满足的函数关系属于二次函数关系的有( )
①设正方形的边长为x面积为y,则y与x有函数关系;
②x个球队参加比赛,每两个队之间比赛一场,则比赛的场次数y与x之间有函数关系;
③设正方体的棱长为x,表面积为y,则y与x有函数关系;
④若一辆汽车以120km/h的速度匀速行驶,那么汽车行驶的里程y(km)与行驶时间x(h)有函数关系.
A.1个
B.2个
C.3个
D.4个
4.与y=2(x﹣1)2+3形状相同的抛物线解析式为( )
A.y=1+x2
B.y=(2x+1)2
C.y=(x﹣1)2
D.y=2x2
5.已知二次函数y=mx2+(2m+1)x+m﹣1的图象与x轴有两个交点,则m的取值范围是( )
A.m<
B.
C.m>﹣且m≠0
D.m≤且m≠0
6.二次函数y=4x2﹣x+1的图象与x轴的交点个数是( )
A.1个
B.2个
C.0个
D.无法确定
7.如图,在△ABC中,AB=AC,BC=6,E为AC边上的点且AE=2EC,点D在BC边上且满足BD=DE,设BD=y,S△ABC=x,则y与x的函数关系式为( )
A.y=x2+
B.y=x2+
C.y=x2+2
D.y=x2+2
8.如图,关于x的二次函数y=x2﹣x+m的图象交x轴的正半轴于A,B两点,交y轴的正半轴于C点,如果x=a时,y<0,那么关于x的一次函数y=(a﹣1)x+m的图象可能是( )
A.
B.
C.
D.
9.抛物线y=x2﹣2x+1的对称轴是( )
A.直线x=1
B.直线x=﹣1
C.直线x=2
D.直线x=﹣2
10.在同一平面直角坐标系中,函数y=ax2﹣bx与y=bx+a的图象可能是( )
A.
B.
C.
D.
二.填空题
11.若是二次函数,则m的值是
.
12.如图,某农场要盖一排三间长方形的羊圈,打算一面利用旧墙,其余各面用木材围成栅栏,该计划用木材围成总长24m的栅栏,设面积为s(m2),垂直于墙的一边长为x(m)米.则s关于x的函数关系式:
(并写出自变量的取值范围)
13.若函数y=(m﹣2)x是反比例函数,则m=
.
14.如果函数y=(k﹣3)+kx+1是二次函数,那么k的值一定是
.
15.抛物线y=x2+8x﹣4与直线x=﹣4的交点坐标是
.
16.已知二次函数y=ax2﹣2的图象经过点(1,﹣1),则a的值为
.
17.抛物线y=x2﹣3的顶点坐标是
.
18.若函数y=mx2+2(m+2)x+m+1的图象与x轴只有一个交点,那么m的值为
.
19.如图所示,在同一平面直角坐标系中,作出①y=﹣3x2,②y=﹣,③y=﹣x2的图象,则从里到外的三条抛物线对应的函数依次是
(填序号)
20.已知抛物线y=x2﹣4x+m与x轴交于A、B两点,若A的坐标是(﹣1,0),则B的坐标是
.
三.解答题
21.已知关于x的反比例函数.
(1)求m的值;
(2)它的图象位于哪些象限?
22.函数是关于x的二次函数,求m的值.
23.已知抛物线y=﹣x2+bx﹣c的部分图象如图.
(1)求b、c的值;
(2)分别求出抛物线的对称轴和y的最大值.
24.画出函数y=(x﹣2)2﹣1的图象.
25.如图,在平面直角坐标系xOy中,二次函数y=x2+bx+c的图象与x轴,y轴的交点分别为(1,0)和(0,﹣3).
(1)求此二次函数的表达式;
(2)结合函数图象,直接写出当y>﹣3时,x的取值范围.
26.已知函数y=(m2﹣m)x2+(m﹣1)x+m+1.
(1)若这个函数是一次函数,求m的值;
(2)若这个函数是二次函数,则m的值应怎样?
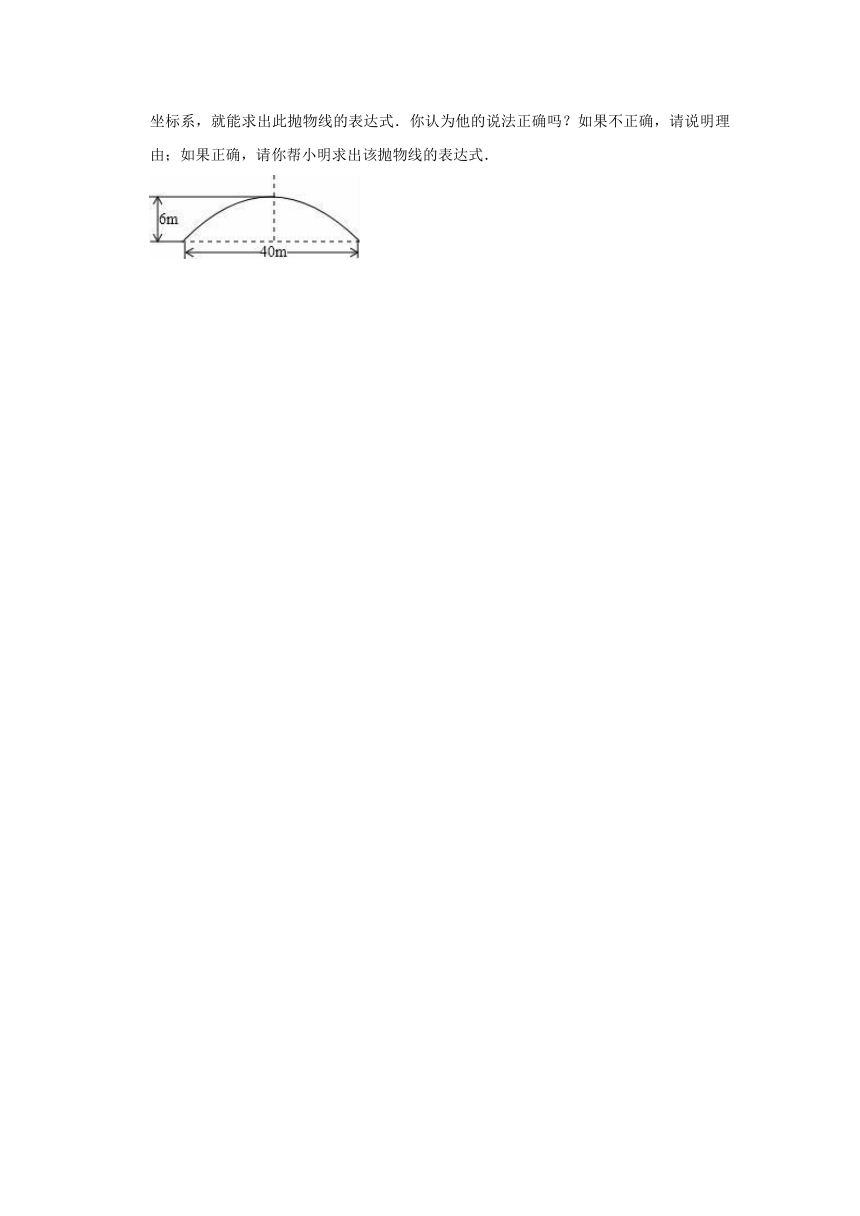
27.如图是把一个抛物线形桥拱,量得两个数据,画在纸上的情形.小明说只要建立适当的坐标系,就能求出此抛物线的表达式.你认为他的说法正确吗?如果不正确,请说明理由;如果正确,请你帮小明求出该抛物线的表达式.
参考答案与试题解析
一.选择题
1.解:A、y=3x﹣1=是反比例函数,故本选项错误;
B、y=﹣是正比例函数,故本选项正确;
C、xy=5是反比例函数,故本选项错误;
D、y=是反比例函数,故本选项错误.
故选:B.
2.解:A、不是二次函数,故此选项错误;
B、不是二次函数,故此选项错误;
C、是二次函数,故此选项正确;
D、当a=0时,不是二次函数,故此选项错误;
故选:C.
3.解:①依题意得:y=x2,属于二次函数关系,故正确;
②依题意得:y=x(x﹣1)=x2﹣x,属于二次函数关系,故正确;
③依题意得:y=6x2,属于二次函数关系,故正确;
④依题意得:y=120x,属于一次函数关系,故错误;
综上所述,两个变量所满足的函数关系属于二次函数关系的有3个.
故选:C.
4.解:y=2(x﹣1)2+3中,a=2.
故选:D.
5.解:∵原函数是二次函数,
∴m≠0
∵二次函数y=mx2+(2m+1)x+m﹣1的图象与x轴有两个交点,则
△=b2﹣4ac>0,
即(2m+1)2﹣4m×(m﹣1)>0,
4m2+4m+1﹣4m2+4m>0,
8m+1>0.
∴m>﹣.
故选:C.
6.解:∵b2﹣4ac=1﹣16<0,
∴抛物线与x轴无交点.
故选:C.
7.解:过A作AH⊥BC,过E作EP⊥BC,则AH∥EP,
∴HC=3,PC=1,BP=5,PE=AH,
∵BD=DE=y,
∴在Rt△EDP中,y2=(5﹣y)2+PE2,
∵x=6AH÷2=3AH,
∴y2=(5﹣y)2+,
∴y=x2+,
故选:A.
8.解:把x=a代入函数y=x2﹣x+m,得y=a2﹣a+m=a(a﹣1)+m,
∵x=a时,y<0,即
a(a﹣1)+m<0.
由图象交y轴的正半轴于点C,得m>0,
即a(a﹣1)<0.
x=a时,y<0,∴a>0,a﹣1<0,
∴一次函数y=(a﹣1)x+m的图象过一二四象限,
故选:A.
9.解:抛物线y=x2﹣2x+1的对称轴为x=﹣=1,
故选:A.
10.解:A、对于直线y=bx+a来说,由图象可以判断,a>0,b>0;而对于抛物线y=ax2﹣bx来说,对称轴x=﹣>0,在y轴的右侧,符合题意,图形正确.
B、对于直线y=bx+a来说,由图象可以判断,a<0,b<0;而对于抛物线y=ax2﹣bx来说,图象应开口向下,故不合题意,图形错误.
C、对于直线y=bx+a来说,由图象可以判断,a<0,b>0;而对于抛物线y=ax2﹣bx来说,对称轴=﹣<0,应位于y轴的左侧,故不合题意,图形错误.
D、对于直线y=bx+a来说,由图象可以判断,a>0,b>0;而对于抛物线y=ax2+bx来说,图象应开口向上,故不合题意,图形错误.
故选:A.
二.填空题
11.解:由题意得:m2﹣2m﹣1=2,且m2+m≠0,
解得:m=3.
故答案为:3.
12.解:根据题意可知,三间羊圈与旧墙平行的一边的总长为(24﹣4x),
则:s=(24﹣4x)x=﹣4x2+24x
由图可知:24﹣4x>0,x>0,
所以x的取值范围是0<x<6,
故答案为:s=﹣4x2+24x(0<x<6).
13.解:∵解:∵函数y=(m﹣2)x是反比例函数,
∴,
解得:m=﹣2.
故答案为:﹣2.
14.解:根据二次函数的定义,得:
k2﹣3k+2=2,
解得k=0或k=3;
又∵k﹣3≠0,
∴k≠3.
∴当k=0时,这个函数是二次函数.
15.解:∵当x=﹣4时,y=(﹣4)2+8×(﹣4)﹣4=﹣20,
∴抛物线y=x2+8x﹣4与直线x=﹣4的交点坐标是(﹣4,﹣20).
16.解:把(1,﹣1)代入函数解析式,得
a﹣2=﹣1,
解得a=1.
故答案是1.
17.解:∵抛物线y=x2﹣3,
∴抛物线y=x2﹣3的顶点坐标是:(0,﹣3),
故答案为:(0,﹣3).
18.解:当m=0时,函数y=4x+1的图象与x轴有一个交点,
当m≠0时,函数y=mx2+2(m+2)x+m+1的图象是抛物线,
若抛物线的图象与x轴只有一个交点,
则方程mx2+2(m+2)x+m+1=0只有一个根,
即4(m+2)2﹣4m(m+1)=0,
解得m=﹣,
综上可得m的值为﹣或0,
故答案为﹣或0.
19.解:①y=﹣3x2,
②y=﹣x2,
③y=﹣x2中,二次项系数a分别为﹣3、﹣、﹣1,
∵|﹣3|>|﹣1|>|﹣|,
∴抛物线②y=﹣x2的开口最宽,抛物线①y=﹣3x2的开口最窄.
故答案为:①③②.
20.解:∵y=x2﹣4x+m,
∴抛物线的对称轴方程为x=2,
∵点A(﹣1,0)和点B关于对称轴x=2对称,
∴点B的坐标为(5,0),
故答案为(5,0).
三.解答题
21.解:(1)∵是关于x的反比例函数,
∴m2﹣5=﹣1,且m﹣2≠0,
∴m的值是﹣2;
(2)当m=﹣2时,m﹣2=﹣2﹣2=﹣4<0,
∴这个反比例函数的图像位于第二、四象限.
22.解:由题意可知
解得:m=2.
23.解:(1)把(1,0),0,3)代入y=﹣x2+bx﹣c得
解得b=﹣2,c=﹣3;
(2)y=﹣x2﹣2x+3
=﹣(x+1)2+4,
所以抛物线的对称轴是直线x=﹣1,最大值为4.
24.解:列表得:
x
…
0
1
2
3
4
…
y
…
3
0
﹣1
0
3
…
如图:
25.解:(1)∵抛物线y=x2+bx+c与x轴、y轴的交点分别为(1,0)和(0,﹣3),
∴,解得:.
∴抛物线的表达式为:y=x2+2x﹣3.
(2)当y>﹣3时,x的取值范围是x<﹣2或x>0.
26.解:(1)根据一次函数的定义,得:m2﹣m=0
解得m=0或m=1
又∵m﹣1≠0即m≠1;
∴当m=0时,这个函数是一次函数;
(2)根据二次函数的定义,得:m2﹣m≠0
解得m1≠0,m2≠1
∴当m1≠0,m2≠1时,这个函数是二次函数.
27.解:正确.
抛物线依坐标系所建不同而各异,如下图.(仅举两例)
二次函数与反比例函数》单元测试卷
一.选择题
1.下列函数不是反比例函数的是( )
A.y=3x﹣1
B.y=﹣
C.xy=5
D.y=
2.下列函数中y是x的二次函数的是( )
A.y=(x+1)(2x﹣1)﹣2x2
B.y=﹣2x+1
C.y=3x2﹣x+5
D.y=ax2+bx+c
3.在下列4个不同的情境中,两个变量所满足的函数关系属于二次函数关系的有( )
①设正方形的边长为x面积为y,则y与x有函数关系;
②x个球队参加比赛,每两个队之间比赛一场,则比赛的场次数y与x之间有函数关系;
③设正方体的棱长为x,表面积为y,则y与x有函数关系;
④若一辆汽车以120km/h的速度匀速行驶,那么汽车行驶的里程y(km)与行驶时间x(h)有函数关系.
A.1个
B.2个
C.3个
D.4个
4.与y=2(x﹣1)2+3形状相同的抛物线解析式为( )
A.y=1+x2
B.y=(2x+1)2
C.y=(x﹣1)2
D.y=2x2
5.已知二次函数y=mx2+(2m+1)x+m﹣1的图象与x轴有两个交点,则m的取值范围是( )
A.m<
B.
C.m>﹣且m≠0
D.m≤且m≠0
6.二次函数y=4x2﹣x+1的图象与x轴的交点个数是( )
A.1个
B.2个
C.0个
D.无法确定
7.如图,在△ABC中,AB=AC,BC=6,E为AC边上的点且AE=2EC,点D在BC边上且满足BD=DE,设BD=y,S△ABC=x,则y与x的函数关系式为( )
A.y=x2+
B.y=x2+
C.y=x2+2
D.y=x2+2
8.如图,关于x的二次函数y=x2﹣x+m的图象交x轴的正半轴于A,B两点,交y轴的正半轴于C点,如果x=a时,y<0,那么关于x的一次函数y=(a﹣1)x+m的图象可能是( )
A.
B.
C.
D.
9.抛物线y=x2﹣2x+1的对称轴是( )
A.直线x=1
B.直线x=﹣1
C.直线x=2
D.直线x=﹣2
10.在同一平面直角坐标系中,函数y=ax2﹣bx与y=bx+a的图象可能是( )
A.
B.
C.
D.
二.填空题
11.若是二次函数,则m的值是
.
12.如图,某农场要盖一排三间长方形的羊圈,打算一面利用旧墙,其余各面用木材围成栅栏,该计划用木材围成总长24m的栅栏,设面积为s(m2),垂直于墙的一边长为x(m)米.则s关于x的函数关系式:
(并写出自变量的取值范围)
13.若函数y=(m﹣2)x是反比例函数,则m=
.
14.如果函数y=(k﹣3)+kx+1是二次函数,那么k的值一定是
.
15.抛物线y=x2+8x﹣4与直线x=﹣4的交点坐标是
.
16.已知二次函数y=ax2﹣2的图象经过点(1,﹣1),则a的值为
.
17.抛物线y=x2﹣3的顶点坐标是
.
18.若函数y=mx2+2(m+2)x+m+1的图象与x轴只有一个交点,那么m的值为
.
19.如图所示,在同一平面直角坐标系中,作出①y=﹣3x2,②y=﹣,③y=﹣x2的图象,则从里到外的三条抛物线对应的函数依次是
(填序号)
20.已知抛物线y=x2﹣4x+m与x轴交于A、B两点,若A的坐标是(﹣1,0),则B的坐标是
.
三.解答题
21.已知关于x的反比例函数.
(1)求m的值;
(2)它的图象位于哪些象限?
22.函数是关于x的二次函数,求m的值.
23.已知抛物线y=﹣x2+bx﹣c的部分图象如图.
(1)求b、c的值;
(2)分别求出抛物线的对称轴和y的最大值.
24.画出函数y=(x﹣2)2﹣1的图象.
25.如图,在平面直角坐标系xOy中,二次函数y=x2+bx+c的图象与x轴,y轴的交点分别为(1,0)和(0,﹣3).
(1)求此二次函数的表达式;
(2)结合函数图象,直接写出当y>﹣3时,x的取值范围.
26.已知函数y=(m2﹣m)x2+(m﹣1)x+m+1.
(1)若这个函数是一次函数,求m的值;
(2)若这个函数是二次函数,则m的值应怎样?
27.如图是把一个抛物线形桥拱,量得两个数据,画在纸上的情形.小明说只要建立适当的坐标系,就能求出此抛物线的表达式.你认为他的说法正确吗?如果不正确,请说明理由;如果正确,请你帮小明求出该抛物线的表达式.
参考答案与试题解析
一.选择题
1.解:A、y=3x﹣1=是反比例函数,故本选项错误;
B、y=﹣是正比例函数,故本选项正确;
C、xy=5是反比例函数,故本选项错误;
D、y=是反比例函数,故本选项错误.
故选:B.
2.解:A、不是二次函数,故此选项错误;
B、不是二次函数,故此选项错误;
C、是二次函数,故此选项正确;
D、当a=0时,不是二次函数,故此选项错误;
故选:C.
3.解:①依题意得:y=x2,属于二次函数关系,故正确;
②依题意得:y=x(x﹣1)=x2﹣x,属于二次函数关系,故正确;
③依题意得:y=6x2,属于二次函数关系,故正确;
④依题意得:y=120x,属于一次函数关系,故错误;
综上所述,两个变量所满足的函数关系属于二次函数关系的有3个.
故选:C.
4.解:y=2(x﹣1)2+3中,a=2.
故选:D.
5.解:∵原函数是二次函数,
∴m≠0
∵二次函数y=mx2+(2m+1)x+m﹣1的图象与x轴有两个交点,则
△=b2﹣4ac>0,
即(2m+1)2﹣4m×(m﹣1)>0,
4m2+4m+1﹣4m2+4m>0,
8m+1>0.
∴m>﹣.
故选:C.
6.解:∵b2﹣4ac=1﹣16<0,
∴抛物线与x轴无交点.
故选:C.
7.解:过A作AH⊥BC,过E作EP⊥BC,则AH∥EP,
∴HC=3,PC=1,BP=5,PE=AH,
∵BD=DE=y,
∴在Rt△EDP中,y2=(5﹣y)2+PE2,
∵x=6AH÷2=3AH,
∴y2=(5﹣y)2+,
∴y=x2+,
故选:A.
8.解:把x=a代入函数y=x2﹣x+m,得y=a2﹣a+m=a(a﹣1)+m,
∵x=a时,y<0,即
a(a﹣1)+m<0.
由图象交y轴的正半轴于点C,得m>0,
即a(a﹣1)<0.
x=a时,y<0,∴a>0,a﹣1<0,
∴一次函数y=(a﹣1)x+m的图象过一二四象限,
故选:A.
9.解:抛物线y=x2﹣2x+1的对称轴为x=﹣=1,
故选:A.
10.解:A、对于直线y=bx+a来说,由图象可以判断,a>0,b>0;而对于抛物线y=ax2﹣bx来说,对称轴x=﹣>0,在y轴的右侧,符合题意,图形正确.
B、对于直线y=bx+a来说,由图象可以判断,a<0,b<0;而对于抛物线y=ax2﹣bx来说,图象应开口向下,故不合题意,图形错误.
C、对于直线y=bx+a来说,由图象可以判断,a<0,b>0;而对于抛物线y=ax2﹣bx来说,对称轴=﹣<0,应位于y轴的左侧,故不合题意,图形错误.
D、对于直线y=bx+a来说,由图象可以判断,a>0,b>0;而对于抛物线y=ax2+bx来说,图象应开口向上,故不合题意,图形错误.
故选:A.
二.填空题
11.解:由题意得:m2﹣2m﹣1=2,且m2+m≠0,
解得:m=3.
故答案为:3.
12.解:根据题意可知,三间羊圈与旧墙平行的一边的总长为(24﹣4x),
则:s=(24﹣4x)x=﹣4x2+24x
由图可知:24﹣4x>0,x>0,
所以x的取值范围是0<x<6,
故答案为:s=﹣4x2+24x(0<x<6).
13.解:∵解:∵函数y=(m﹣2)x是反比例函数,
∴,
解得:m=﹣2.
故答案为:﹣2.
14.解:根据二次函数的定义,得:
k2﹣3k+2=2,
解得k=0或k=3;
又∵k﹣3≠0,
∴k≠3.
∴当k=0时,这个函数是二次函数.
15.解:∵当x=﹣4时,y=(﹣4)2+8×(﹣4)﹣4=﹣20,
∴抛物线y=x2+8x﹣4与直线x=﹣4的交点坐标是(﹣4,﹣20).
16.解:把(1,﹣1)代入函数解析式,得
a﹣2=﹣1,
解得a=1.
故答案是1.
17.解:∵抛物线y=x2﹣3,
∴抛物线y=x2﹣3的顶点坐标是:(0,﹣3),
故答案为:(0,﹣3).
18.解:当m=0时,函数y=4x+1的图象与x轴有一个交点,
当m≠0时,函数y=mx2+2(m+2)x+m+1的图象是抛物线,
若抛物线的图象与x轴只有一个交点,
则方程mx2+2(m+2)x+m+1=0只有一个根,
即4(m+2)2﹣4m(m+1)=0,
解得m=﹣,
综上可得m的值为﹣或0,
故答案为﹣或0.
19.解:①y=﹣3x2,
②y=﹣x2,
③y=﹣x2中,二次项系数a分别为﹣3、﹣、﹣1,
∵|﹣3|>|﹣1|>|﹣|,
∴抛物线②y=﹣x2的开口最宽,抛物线①y=﹣3x2的开口最窄.
故答案为:①③②.
20.解:∵y=x2﹣4x+m,
∴抛物线的对称轴方程为x=2,
∵点A(﹣1,0)和点B关于对称轴x=2对称,
∴点B的坐标为(5,0),
故答案为(5,0).
三.解答题
21.解:(1)∵是关于x的反比例函数,
∴m2﹣5=﹣1,且m﹣2≠0,
∴m的值是﹣2;
(2)当m=﹣2时,m﹣2=﹣2﹣2=﹣4<0,
∴这个反比例函数的图像位于第二、四象限.
22.解:由题意可知
解得:m=2.
23.解:(1)把(1,0),0,3)代入y=﹣x2+bx﹣c得
解得b=﹣2,c=﹣3;
(2)y=﹣x2﹣2x+3
=﹣(x+1)2+4,
所以抛物线的对称轴是直线x=﹣1,最大值为4.
24.解:列表得:
x
…
0
1
2
3
4
…
y
…
3
0
﹣1
0
3
…
如图:
25.解:(1)∵抛物线y=x2+bx+c与x轴、y轴的交点分别为(1,0)和(0,﹣3),
∴,解得:.
∴抛物线的表达式为:y=x2+2x﹣3.
(2)当y>﹣3时,x的取值范围是x<﹣2或x>0.
26.解:(1)根据一次函数的定义,得:m2﹣m=0
解得m=0或m=1
又∵m﹣1≠0即m≠1;
∴当m=0时,这个函数是一次函数;
(2)根据二次函数的定义,得:m2﹣m≠0
解得m1≠0,m2≠1
∴当m1≠0,m2≠1时,这个函数是二次函数.
27.解:正确.
抛物线依坐标系所建不同而各异,如下图.(仅举两例)
