2021-2022学年鲁教五四新版九年级上册数学《第1章 反比例函数》单元测试卷(word版含解析)
文档属性
| 名称 | 2021-2022学年鲁教五四新版九年级上册数学《第1章 反比例函数》单元测试卷(word版含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 408.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-16 00:00:00 | ||
图片预览

文档简介
2021-2022学年鲁教五四新版九年级上册数学《第1章
反比例函数》单元测试卷
一.选择题
1.已知y=2x2m是反比例函数,则m的值是( )
A.m=
B.m=﹣
C.m≠0
D.一切实数
2.如图,有反比例函数y=,y=﹣的图象和一个圆,则图中阴影部分的面积是( )
A.π
B.2π
C.4π
D.条件不足,无法求
3.下面每个选项中的两种量成反比例的是( )
A.A和B互为倒数
B.圆柱的高一定,体积和底面积
C.被减数一定,减数和差
D.除数一定,商和被除数
4.已知反比例函数y=的图象过点P(2,﹣3),则该反比例函数的图象位于( )
A.第一、二象限
B.第一、三象限
C.第二、四象限
D.第三、四象限
5.下列函数中,y是x的反比例函数的为( )
A.y=2x+1
B.
C.
D.y=2x2﹣1
6.下列说法正确的是( )
A.函数y=2x的图象是过原点的射线
B.直线y=﹣x+2经过第一、二、三象限
C.函数y=(x<0),y随x增大而增大
D.函数y=2x﹣3,y随x增大而减小
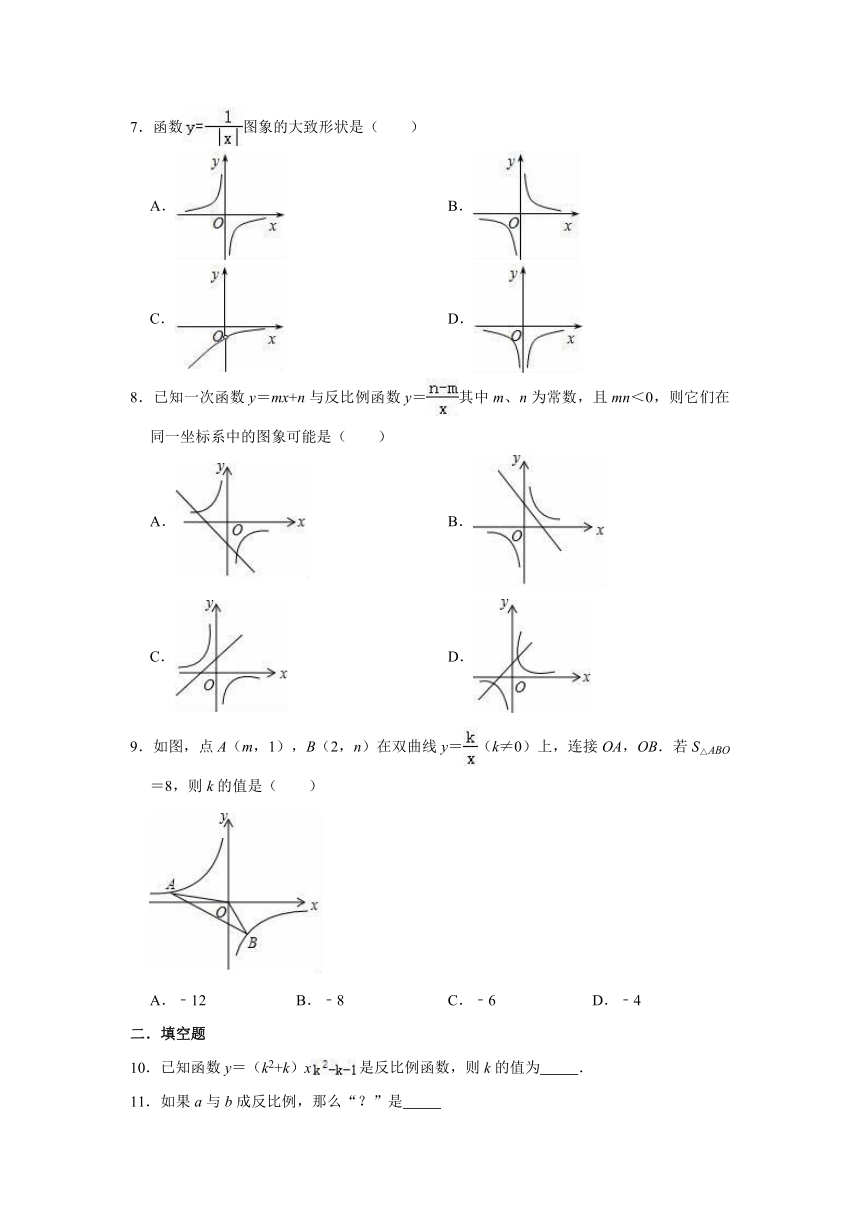
7.函数图象的大致形状是( )
A.
B.
C.
D.
8.已知一次函数y=mx+n与反比例函数y=其中m、n为常数,且mn<0,则它们在同一坐标系中的图象可能是( )
A.
B.
C.
D.
9.如图,点A(m,1),B(2,n)在双曲线y=(k≠0)上,连接OA,OB.若S△ABO=8,则k的值是( )
A.﹣12
B.﹣8
C.﹣6
D.﹣4
二.填空题
10.已知函数y=(k2+k)x是反比例函数,则k的值为
.
11.如果a与b成反比例,那么“?”是
a
4
?
b
200
160
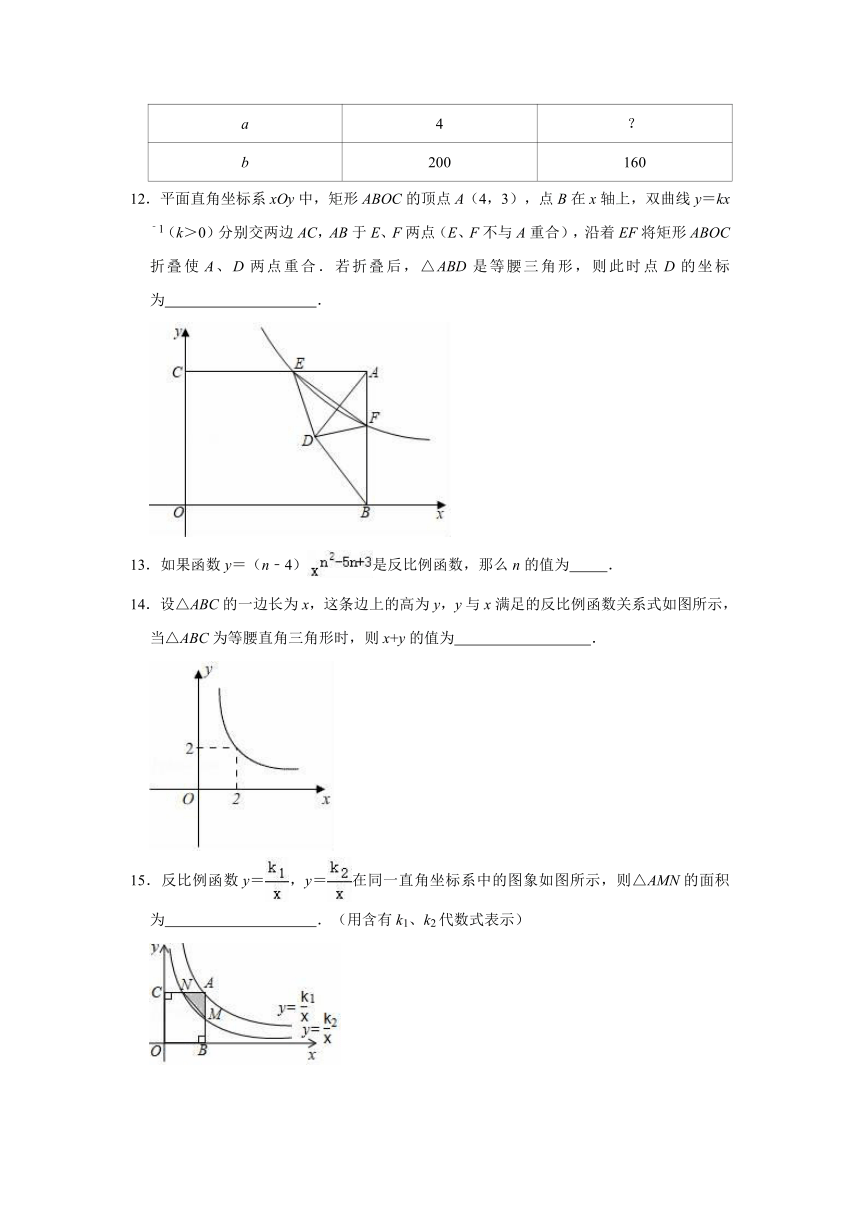
12.平面直角坐标系xOy中,矩形ABOC的顶点A(4,3),点B在x轴上,双曲线y=kx﹣1(k>0)分别交两边AC,AB于E、F两点(E、F不与A重合),沿着EF将矩形ABOC折叠使A、D两点重合.若折叠后,△ABD是等腰三角形,则此时点D的坐标为
.
13.如果函数y=(n﹣4)是反比例函数,那么n的值为
.
14.设△ABC的一边长为x,这条边上的高为y,y与x满足的反比例函数关系式如图所示,当△ABC为等腰直角三角形时,则x+y的值为
.
15.反比例函数y=,y=在同一直角坐标系中的图象如图所示,则△AMN的面积为
.(用含有k1、k2代数式表示)
16.如图,点A(1,n)和点B都在反比例函数y=(x>0)的图象上,若∠OAB=90°,,则k的值是
.
三.解答题
17.若反比例函数y=(m2﹣5)x在每一个象限内,y随x的增大而增大.求m的值.
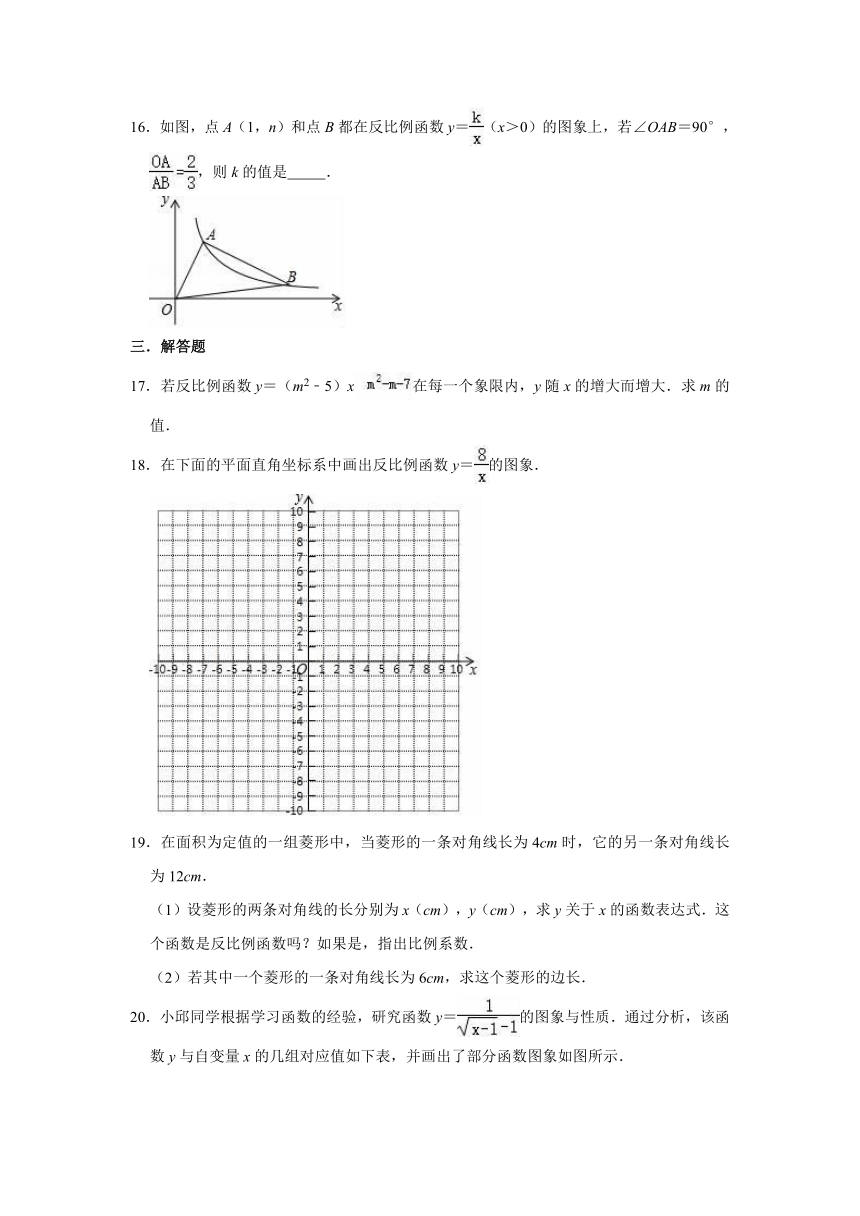
18.在下面的平面直角坐标系中画出反比例函数y=的图象.
19.在面积为定值的一组菱形中,当菱形的一条对角线长为4cm时,它的另一条对角线长为12cm.
(1)设菱形的两条对角线的长分别为x(cm),y(cm),求y关于x的函数表达式.这个函数是反比例函数吗?如果是,指出比例系数.
(2)若其中一个菱形的一条对角线长为6cm,求这个菱形的边长.
20.小邱同学根据学习函数的经验,研究函数y=的图象与性质.通过分析,该函数y与自变量x的几组对应值如下表,并画出了部分函数图象如图所示.
x
1
3
4
5
6
…
y
﹣1
﹣2
﹣3.4
﹣7.5
2.4
1.4
1
0.8
…
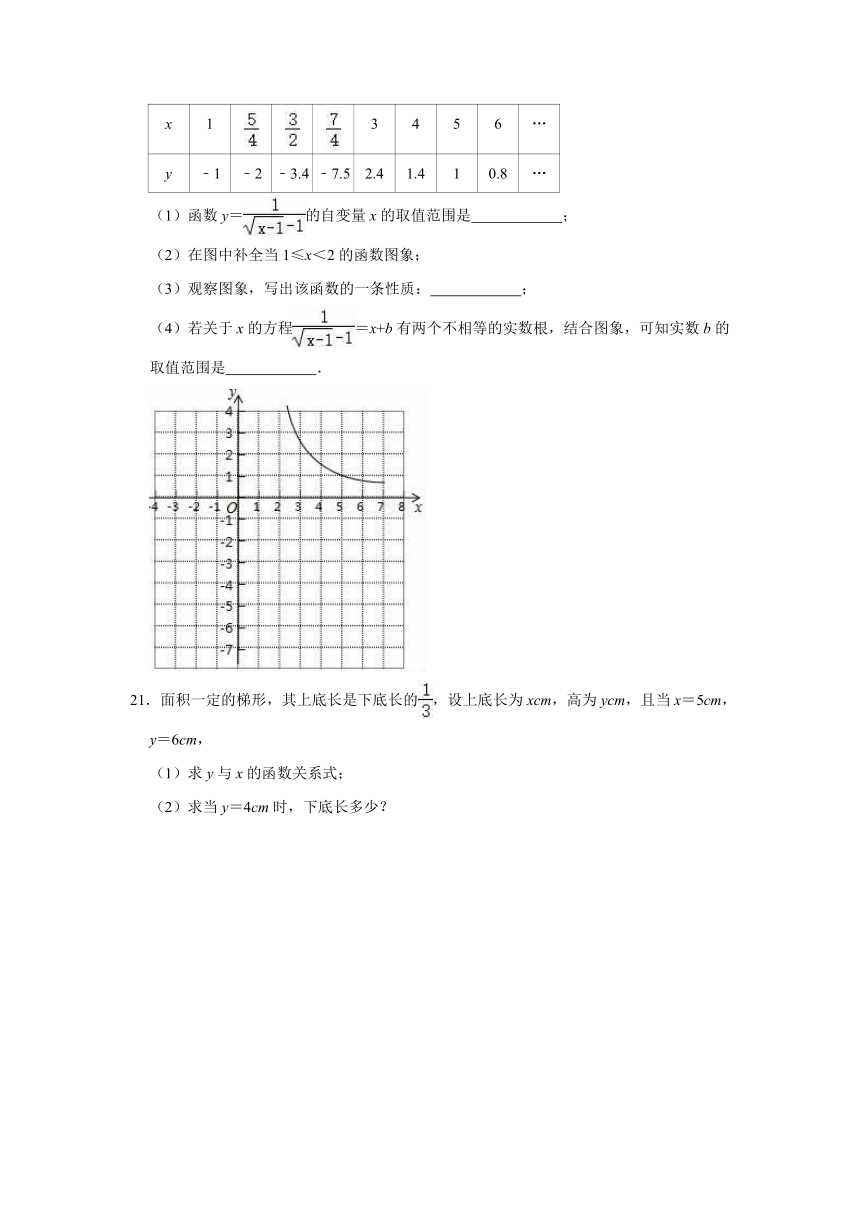
(1)函数y=的自变量x的取值范围是
;
(2)在图中补全当1≤x<2的函数图象;
(3)观察图象,写出该函数的一条性质:
;
(4)若关于x的方程=x+b有两个不相等的实数根,结合图象,可知实数b的取值范围是
.
21.面积一定的梯形,其上底长是下底长的,设上底长为xcm,高为ycm,且当x=5cm,y=6cm,
(1)求y与x的函数关系式;
(2)求当y=4cm时,下底长多少?
参考答案与试题解析
一.选择题
1.解:y=2x2m是反比例函数,则2m=﹣1,所以.
故选:B.
2.解:根据反比例函数的图象的对称性和圆的对称性得出:图中阴影部分的面积等于圆的面积的一半,
∵圆的半径是2,
∴图中阴影部分的面积是×π×22=2π.
故选:B.
3.解:A.因为A和B互为倒数,所以A×B=1,符合题意;
B.圆柱的体积÷底面积=高,不是乘积,不符合题意;
C.减数+差=被减数,不是乘积,不符合题意;
D.被除数÷商=除数,不是乘积,不符合题意.
故选:A.
4.解:∵反比例函数y=(k≠0)的图象经过点P(2,﹣3),
∴k=2×(﹣3)=﹣6<0,
∴该反比例函数经过第二、四象限.
故选:C.
5.解:A、y=2x+1是一次函数,故此选项不符合题意;
B、自变量x的指数是2,不是反比例函数,故此选项不符合题意;
C、符合反比例函数的定义,y是x的反比例函数,故此选项符合题意;
D、y=2x2﹣1是二次函数,故此选项不符合题意.
故选:C.
6.解:A、函数y=2x的图象是过原点的直线,原说法错误,故此选项不符合题意;
B、直线y=﹣x+2经过第一、二、四象限,原说法错误,故此选项不符合题意;
C、函数y=﹣(x<0),y随x增大而增大,原说法正确,故此选项符合题意;
D、函数y=2x﹣3,y随x增大而增大,原说法错误,故此选项不符合题意.
故选:C.
7.解:由函数解析式可得x可取正数,也可取负数,但函数值只能是负数;
所以函数图象应在x轴下方,并且x,y均不为0.
故选:D.
8.解:A、由一次函数图象过二、三、四象限,得m<0,交y轴负半轴,则n<0,
此时mn>0,不合题意;故本选项错误;
B、由一次函数图象过一、二、四象限,得m<0,交y轴正半轴,则n>0,满足mn<0,
∵m<0,n>0,
∴n﹣m>0,
∴反比例函数y=的图象过一、三象限,故本选项正确;
C、由一次函数图象过一、二、三象限,得m>0,交y轴正半轴,则n>0,
此时,mn>0,不合题意;故本选项错误;
D、由一次函数图象过一、二、三象限,得m>0,交y轴正半轴,则n>0,
此时,mn>0,不合题意;故本选项错误;
故选:B.
9.解:过A作y轴的垂线,过B作x轴的垂线,交于点C,连接OC,
设A(k,1),B(2,
k),则AC=2﹣k,BC=1﹣k,
∵S△ABO=8,
∴S△ABC﹣S△ACO﹣S△BOC=8,
即(2﹣k)(1﹣k)﹣(2﹣k)×1﹣(1﹣k)×2=8,
解得k=±6,
∵k<0,
∴k=﹣6,
故选:C.
二.填空题
10.解:由题意得:k2﹣k﹣1=﹣1,且k2+k≠0,
解得:k=1,
故答案为:1.
11.解:∵a与b成反比例,
∴ab=4×200=800,
∴“?”是=5,
故答案为:5.
12.解:过D点作DN⊥AB,
①当BD=AD时,如图3,有∠AND=90°,AN=BN=AB=,
∴∠DAN+∠ADN=90°,
∵∠DAN+∠AFM=90°,
∴∠ADN=∠AFM,
∴tan∠ADN=tan∠AFM=,
∴,
∵AN=,
∴DN=,
∴D(4﹣,
),即D(,
);
②当AB=AD=3时,如图4,
在Rt△ADN中,sin∠ADN=sin∠AFM=,
∴,
∴AN=AD=×3=,
∴BN=3﹣AN=3﹣=,
∵DN=AN=×=,
∴D(4﹣,
),即D(,
);
③当AB=BD时,△AEF≌△DEF,
∴DF=AF,
∴DF+BF=AF+BF,即DF+BF=AB,
∴DF+BF=BD,
此时D、F、B三点共线且F点与B点重合,不符合题意舍去,
∴AB≠BD,
综上所述,所求D点坐标为(,
)或(,
).
13.解:根据题意得:n2﹣5n+3=﹣1且n﹣4≠0,
解得:n=1,
故答案是:1.
14.解:由反比例函数的图象得xy=4,当等腰直角△ABC的斜边为底时,该底边上的高为这个底的一半,
即x=2y,2y2=4,
解得:y=,
则x=2,
∴x+y=3;
当等腰直角△ABC的一条直角边为底时,该底边上的高为另一条直角边,
即x=y,y2=4,
解得:y=2,
则x=2,
∴x+y=4,
综上知x+y的值为4或3.
故答案为:4或3.
15.解:设A(a,),则M(a,),N(a,),
∴AN=a﹣a,AM=﹣,
∴△AMN的面积=AN×AM=×(a﹣a)×(﹣)=,
故答案为:.
16.解:如图,过A作AC⊥x轴,过B作BD⊥AC于D,则∠ACO=∠BDA=90°,OC=1,AC=n,
∵∠BAO=90°,
∴∠CAO+∠BAC=∠ABD+∠BAC=90°,
∴∠CAO=∠DBA,
∴△AOC∽△BAD,
∴==,即,
∴AD=,BD=,
∴B(1+,n﹣),
∵k=1×n=(1+)(n﹣),
解得n=2或n=﹣0.5(舍去),
∴k=1×2=2,
故答案为:2.
三.解答题
17.解:根据题意,得m2﹣5<0,m2﹣m﹣7=﹣1,
﹣,m1=3(不符合题意,舍),m2=﹣2,
∴m=﹣2.
18.解:列表:
描点,连线:
19.解:(1)∵在面积为定值的一组菱形中,当菱形的一条对角线长为4cm时,它的另一条对角线长为12cm,
∴S菱形=×4×12=24,
∵菱形的两条对角线的长分别为x,y,
∴S菱形=xy=24,
∴y关于x的函数表达式为:y=;
这个函数是反比例函数,比例系数是48.
(2)∵其中一个菱形的一条对角线长为6cm,
∴另一条对角线长为:=8(cm),
∴这个菱形的边长为:=5(cm),
∴这个菱形的边长5cm.
20.解:(1)由x﹣1≥0且x﹣1≠1,可得x≥1且x≠2;
(2)当1≤x<2的函数图象如图所示:
(3)由图可得,当1≤x<2(或x>2)时,函数图象从左往右下降,即y随x的增大而减小;
(4)关于x的方程=x+b有两个不相等的实数根,结合图象,可知实数b的取值范围是b≤﹣2.
故答案为:x≥1且x≠2;当1≤x<2(或x>2)时,y随x的增大而减小;b≤﹣2.
21.解:(1)∵x=5cm,y=6cm,上底长是下底长的,
∴下底长为15cm,
∴梯形的面积=×(5+15)×6=60,
∴梯形的高=
∴y==;
(2)当y=4cm时,x=7.5,
∴3x=22.5.
答:下底长22.5cm.
反比例函数》单元测试卷
一.选择题
1.已知y=2x2m是反比例函数,则m的值是( )
A.m=
B.m=﹣
C.m≠0
D.一切实数
2.如图,有反比例函数y=,y=﹣的图象和一个圆,则图中阴影部分的面积是( )
A.π
B.2π
C.4π
D.条件不足,无法求
3.下面每个选项中的两种量成反比例的是( )
A.A和B互为倒数
B.圆柱的高一定,体积和底面积
C.被减数一定,减数和差
D.除数一定,商和被除数
4.已知反比例函数y=的图象过点P(2,﹣3),则该反比例函数的图象位于( )
A.第一、二象限
B.第一、三象限
C.第二、四象限
D.第三、四象限
5.下列函数中,y是x的反比例函数的为( )
A.y=2x+1
B.
C.
D.y=2x2﹣1
6.下列说法正确的是( )
A.函数y=2x的图象是过原点的射线
B.直线y=﹣x+2经过第一、二、三象限
C.函数y=(x<0),y随x增大而增大
D.函数y=2x﹣3,y随x增大而减小
7.函数图象的大致形状是( )
A.
B.
C.
D.
8.已知一次函数y=mx+n与反比例函数y=其中m、n为常数,且mn<0,则它们在同一坐标系中的图象可能是( )
A.
B.
C.
D.
9.如图,点A(m,1),B(2,n)在双曲线y=(k≠0)上,连接OA,OB.若S△ABO=8,则k的值是( )
A.﹣12
B.﹣8
C.﹣6
D.﹣4
二.填空题
10.已知函数y=(k2+k)x是反比例函数,则k的值为
.
11.如果a与b成反比例,那么“?”是
a
4
?
b
200
160
12.平面直角坐标系xOy中,矩形ABOC的顶点A(4,3),点B在x轴上,双曲线y=kx﹣1(k>0)分别交两边AC,AB于E、F两点(E、F不与A重合),沿着EF将矩形ABOC折叠使A、D两点重合.若折叠后,△ABD是等腰三角形,则此时点D的坐标为
.
13.如果函数y=(n﹣4)是反比例函数,那么n的值为
.
14.设△ABC的一边长为x,这条边上的高为y,y与x满足的反比例函数关系式如图所示,当△ABC为等腰直角三角形时,则x+y的值为
.
15.反比例函数y=,y=在同一直角坐标系中的图象如图所示,则△AMN的面积为
.(用含有k1、k2代数式表示)
16.如图,点A(1,n)和点B都在反比例函数y=(x>0)的图象上,若∠OAB=90°,,则k的值是
.
三.解答题
17.若反比例函数y=(m2﹣5)x在每一个象限内,y随x的增大而增大.求m的值.
18.在下面的平面直角坐标系中画出反比例函数y=的图象.
19.在面积为定值的一组菱形中,当菱形的一条对角线长为4cm时,它的另一条对角线长为12cm.
(1)设菱形的两条对角线的长分别为x(cm),y(cm),求y关于x的函数表达式.这个函数是反比例函数吗?如果是,指出比例系数.
(2)若其中一个菱形的一条对角线长为6cm,求这个菱形的边长.
20.小邱同学根据学习函数的经验,研究函数y=的图象与性质.通过分析,该函数y与自变量x的几组对应值如下表,并画出了部分函数图象如图所示.
x
1
3
4
5
6
…
y
﹣1
﹣2
﹣3.4
﹣7.5
2.4
1.4
1
0.8
…
(1)函数y=的自变量x的取值范围是
;
(2)在图中补全当1≤x<2的函数图象;
(3)观察图象,写出该函数的一条性质:
;
(4)若关于x的方程=x+b有两个不相等的实数根,结合图象,可知实数b的取值范围是
.
21.面积一定的梯形,其上底长是下底长的,设上底长为xcm,高为ycm,且当x=5cm,y=6cm,
(1)求y与x的函数关系式;
(2)求当y=4cm时,下底长多少?
参考答案与试题解析
一.选择题
1.解:y=2x2m是反比例函数,则2m=﹣1,所以.
故选:B.
2.解:根据反比例函数的图象的对称性和圆的对称性得出:图中阴影部分的面积等于圆的面积的一半,
∵圆的半径是2,
∴图中阴影部分的面积是×π×22=2π.
故选:B.
3.解:A.因为A和B互为倒数,所以A×B=1,符合题意;
B.圆柱的体积÷底面积=高,不是乘积,不符合题意;
C.减数+差=被减数,不是乘积,不符合题意;
D.被除数÷商=除数,不是乘积,不符合题意.
故选:A.
4.解:∵反比例函数y=(k≠0)的图象经过点P(2,﹣3),
∴k=2×(﹣3)=﹣6<0,
∴该反比例函数经过第二、四象限.
故选:C.
5.解:A、y=2x+1是一次函数,故此选项不符合题意;
B、自变量x的指数是2,不是反比例函数,故此选项不符合题意;
C、符合反比例函数的定义,y是x的反比例函数,故此选项符合题意;
D、y=2x2﹣1是二次函数,故此选项不符合题意.
故选:C.
6.解:A、函数y=2x的图象是过原点的直线,原说法错误,故此选项不符合题意;
B、直线y=﹣x+2经过第一、二、四象限,原说法错误,故此选项不符合题意;
C、函数y=﹣(x<0),y随x增大而增大,原说法正确,故此选项符合题意;
D、函数y=2x﹣3,y随x增大而增大,原说法错误,故此选项不符合题意.
故选:C.
7.解:由函数解析式可得x可取正数,也可取负数,但函数值只能是负数;
所以函数图象应在x轴下方,并且x,y均不为0.
故选:D.
8.解:A、由一次函数图象过二、三、四象限,得m<0,交y轴负半轴,则n<0,
此时mn>0,不合题意;故本选项错误;
B、由一次函数图象过一、二、四象限,得m<0,交y轴正半轴,则n>0,满足mn<0,
∵m<0,n>0,
∴n﹣m>0,
∴反比例函数y=的图象过一、三象限,故本选项正确;
C、由一次函数图象过一、二、三象限,得m>0,交y轴正半轴,则n>0,
此时,mn>0,不合题意;故本选项错误;
D、由一次函数图象过一、二、三象限,得m>0,交y轴正半轴,则n>0,
此时,mn>0,不合题意;故本选项错误;
故选:B.
9.解:过A作y轴的垂线,过B作x轴的垂线,交于点C,连接OC,
设A(k,1),B(2,
k),则AC=2﹣k,BC=1﹣k,
∵S△ABO=8,
∴S△ABC﹣S△ACO﹣S△BOC=8,
即(2﹣k)(1﹣k)﹣(2﹣k)×1﹣(1﹣k)×2=8,
解得k=±6,
∵k<0,
∴k=﹣6,
故选:C.
二.填空题
10.解:由题意得:k2﹣k﹣1=﹣1,且k2+k≠0,
解得:k=1,
故答案为:1.
11.解:∵a与b成反比例,
∴ab=4×200=800,
∴“?”是=5,
故答案为:5.
12.解:过D点作DN⊥AB,
①当BD=AD时,如图3,有∠AND=90°,AN=BN=AB=,
∴∠DAN+∠ADN=90°,
∵∠DAN+∠AFM=90°,
∴∠ADN=∠AFM,
∴tan∠ADN=tan∠AFM=,
∴,
∵AN=,
∴DN=,
∴D(4﹣,
),即D(,
);
②当AB=AD=3时,如图4,
在Rt△ADN中,sin∠ADN=sin∠AFM=,
∴,
∴AN=AD=×3=,
∴BN=3﹣AN=3﹣=,
∵DN=AN=×=,
∴D(4﹣,
),即D(,
);
③当AB=BD时,△AEF≌△DEF,
∴DF=AF,
∴DF+BF=AF+BF,即DF+BF=AB,
∴DF+BF=BD,
此时D、F、B三点共线且F点与B点重合,不符合题意舍去,
∴AB≠BD,
综上所述,所求D点坐标为(,
)或(,
).
13.解:根据题意得:n2﹣5n+3=﹣1且n﹣4≠0,
解得:n=1,
故答案是:1.
14.解:由反比例函数的图象得xy=4,当等腰直角△ABC的斜边为底时,该底边上的高为这个底的一半,
即x=2y,2y2=4,
解得:y=,
则x=2,
∴x+y=3;
当等腰直角△ABC的一条直角边为底时,该底边上的高为另一条直角边,
即x=y,y2=4,
解得:y=2,
则x=2,
∴x+y=4,
综上知x+y的值为4或3.
故答案为:4或3.
15.解:设A(a,),则M(a,),N(a,),
∴AN=a﹣a,AM=﹣,
∴△AMN的面积=AN×AM=×(a﹣a)×(﹣)=,
故答案为:.
16.解:如图,过A作AC⊥x轴,过B作BD⊥AC于D,则∠ACO=∠BDA=90°,OC=1,AC=n,
∵∠BAO=90°,
∴∠CAO+∠BAC=∠ABD+∠BAC=90°,
∴∠CAO=∠DBA,
∴△AOC∽△BAD,
∴==,即,
∴AD=,BD=,
∴B(1+,n﹣),
∵k=1×n=(1+)(n﹣),
解得n=2或n=﹣0.5(舍去),
∴k=1×2=2,
故答案为:2.
三.解答题
17.解:根据题意,得m2﹣5<0,m2﹣m﹣7=﹣1,
﹣,m1=3(不符合题意,舍),m2=﹣2,
∴m=﹣2.
18.解:列表:
描点,连线:
19.解:(1)∵在面积为定值的一组菱形中,当菱形的一条对角线长为4cm时,它的另一条对角线长为12cm,
∴S菱形=×4×12=24,
∵菱形的两条对角线的长分别为x,y,
∴S菱形=xy=24,
∴y关于x的函数表达式为:y=;
这个函数是反比例函数,比例系数是48.
(2)∵其中一个菱形的一条对角线长为6cm,
∴另一条对角线长为:=8(cm),
∴这个菱形的边长为:=5(cm),
∴这个菱形的边长5cm.
20.解:(1)由x﹣1≥0且x﹣1≠1,可得x≥1且x≠2;
(2)当1≤x<2的函数图象如图所示:
(3)由图可得,当1≤x<2(或x>2)时,函数图象从左往右下降,即y随x的增大而减小;
(4)关于x的方程=x+b有两个不相等的实数根,结合图象,可知实数b的取值范围是b≤﹣2.
故答案为:x≥1且x≠2;当1≤x<2(或x>2)时,y随x的增大而减小;b≤﹣2.
21.解:(1)∵x=5cm,y=6cm,上底长是下底长的,
∴下底长为15cm,
∴梯形的面积=×(5+15)×6=60,
∴梯形的高=
∴y==;
(2)当y=4cm时,x=7.5,
∴3x=22.5.
答:下底长22.5cm.
