2.1 锐角三角函数同步练习(含答案)
图片预览


文档简介
中小学教育资源及组卷应用平台
第二章
直角三角形的边角关系
1
锐角三角函数
知识能力全练
知识点一
正切
1.在Rt△ABC中,∠C=90°,a5,b=12,则tanB的值为(
)
A.
B.
C.
D.
2.如图所示,在△ABC中,AD⊥BC交BC于点D,AD=BD,若AB=4,tanC=,则BC=(
)
A.8
B.8
C.7
D.7
3.如图所示,△ABC的顶点在正方形网格的格点上,则tanA的值为(
)
A.
B.
C.2
D.
4.在Rt△ABC中,∠C=90°,若tanA=,则tanB=___________.
5.在Rt△ABC中,∠C=90°,AC=4
cm,tanB=,求BC、AB的长.
识点二
坡度、坡角
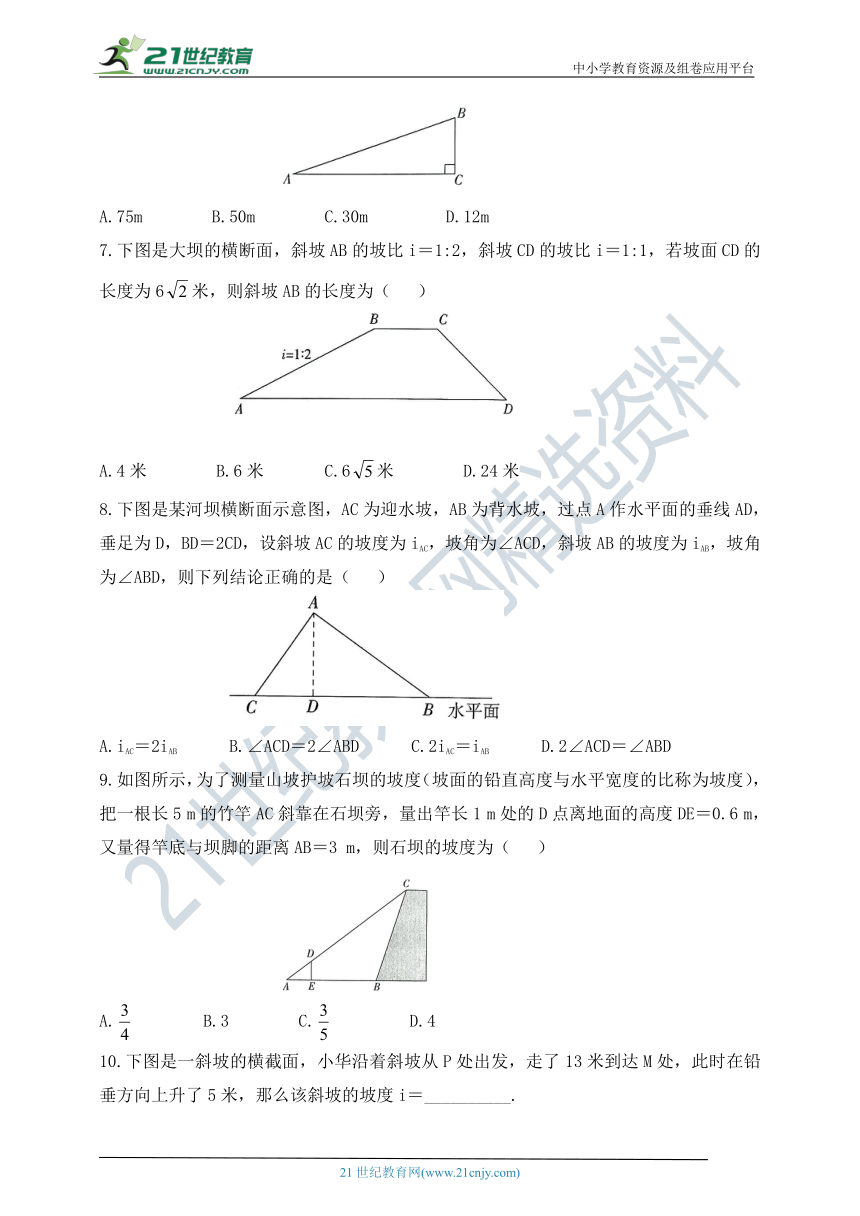
6.如图所示,有一斜坡AB,坡顶B离地面的高度BC为30
m,斜坡的倾斜角是∠BAC,若tan∠BAC=,则此斜坡的水平距离AC为(
)
A.75m
B.50m
C.30m
D.12m
7.下图是大坝的横断面,斜坡AB的坡比i=1:2,斜坡CD的坡比i=1:1,若坡面CD的长度为6米,则斜坡AB的长度为(
)
A.4米
B.6米
C.6米
D.24米
8.下图是某河坝横断面示意图,AC为迎水坡,AB为背水坡,过点A作水平面的垂线AD,垂足为D,BD=2CD,设斜坡AC的坡度为iAC,坡角为∠ACD,斜坡AB的坡度为iAB,坡角为∠ABD,则下列结论正确的是(
)
A.iAC=2iAB
B.∠ACD=2∠ABD
C.2iAC=iAB
D.2∠ACD=∠ABD
9.如图所示,为了测量山坡护坡石坝的坡度(坡面的铅直高度与水平宽度的比称为坡度),把一根长5
m的竹竿AC斜靠在石坝旁,量出竿长1
m处的D点离地面的高度DE=0.6
m,又量得竿底与坝脚的距离AB=3
m,则石坝的坡度为(
)
A.
B.3
C.
D.4
10.下图是一斜坡的横截面,小华沿着斜坡从P处出发,走了13米到达M处,此时在铅垂方向上升了5米,那么该斜坡的坡度i=__________.
知识点三
正弦、余弦
11.在台风来临之前,有关部门用钢管加固树木(如图所示),固定点A离地面的高度AC=m,钢管与地面所成角∠ABC=∠1,那么钢管AB的长为(
)
A.
B.
C.m·cos∠1
D.m·sin∠1
12.在正方形网格中,△ABC的位置如图所示,则cosB的值为(
)
A.
B.
C.
D.
13.如图所示,一块矩形木板ABCD斜靠在墙边(OC⊥OB,点A,B,C,D,O在同一平面内)已知AB=a,AD=b,∠BCO=x,则点A到OC的距离等于(
)
A.asinx+bsinx
B.acosx+bcosx
C.asinx+bcosx
D.acosx+bsinx
14.如图所示,△ABC中,∠C=90°,BC=2AC,则cosA=(
)
A.
B.
C.
D.
15.比较大小:sin81°_______tan47°(填“<”“=”或“>”).
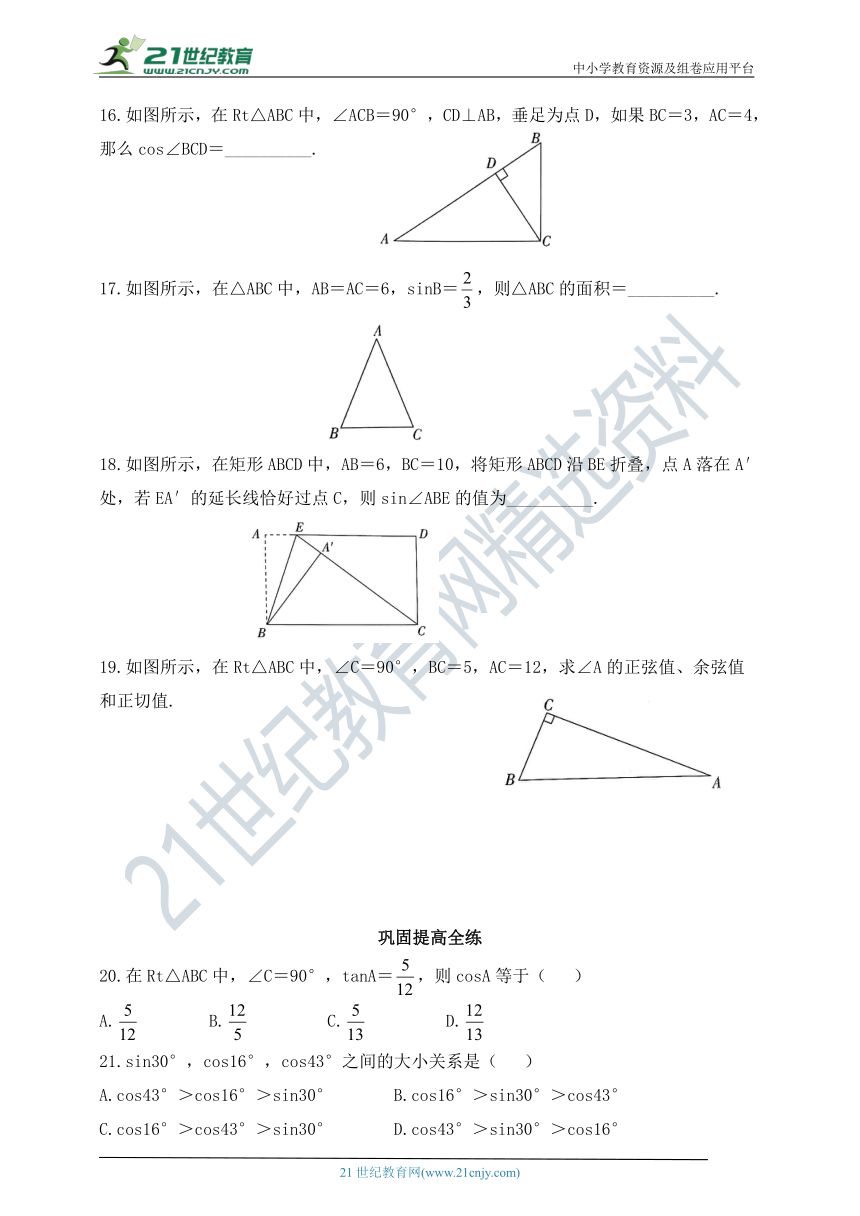
16.如图所示,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为点D,如果BC=3,AC=4,那么cos∠BCD=__________.
17.如图所示,在△ABC中,AB=AC=6,sinB=,则△ABC的面积=__________.
18.如图所示,在矩形ABCD中,AB=6,BC=10,将矩形ABCD沿BE折叠,点A落在A′处,若EA′的延长线恰好过点C,则sin∠ABE的值为__________.
19.如图所示,在Rt△ABC中,∠C=90°,BC=5,AC=12,求∠A的正弦值、余弦值
和正切值.
巩固提高全练
20.在Rt△ABC中,∠C=90°,tanA=,则cosA等于(
)
A.
B.
C.
D.
21.sin30°,cos16°,cos43°之间的大小关系是(
)
A.cos43°>cos16°>sin30°
B.cos16°>sin30°>cos43°
C.cos16°>cos43°>sin30°
D.cos43°>sin30°>cos16°
22.如图所示,在Rt△ABC中,CD是斜边AB上的中线,已知CD=2,AC=3,则sinB的值是(
)
A.
B.
C.
D.
23.如图所示,△ABC的三个顶点均在格点上,则cosA的值为(
)
A.
B.
C.2
D.
24.如图所示,为了测量一条河流的宽度,一测量员在河岸边相距200米的P,Q两点分别测定对岸一棵树T的位置,T在P的正北方向,且T在Q的北偏西70°方向,则河宽(PT的长)可以表示为(
)
A.200tan70°米
B.米
C.200sin70°米
D.米
25.如图所示,在4×5的正方形网格中,每个小正方形的边长都是1,△ABC的顶点都在这些小正方形的顶点上,那么sin∠ACB的值为(
)
A.
B.
C.
D.
26.如图所示,矩形ABCD的四个顶点分别在直线3,4,2,1上若直线1∥2∥3∥4且间距相等,AB=4,BC=3,则tana的值为(
)
A.
B.
C.
D.
27.如图所示,点C在线段AB上,且AC=2BC,分别以AC,BC为边在线段AB的同侧作正方形ACDE,BCFG,连接EC,EG,则tan∠CEG=____________.
28.如图所示,在4×4的网格中,每个小正方形的边长为1,线段AB、CD的端点均为格点.
(1)AB的长度为__________,CD的长度为___________;
(2)若AB与CD所夹锐角为aα,求tana的值.
29.问题呈现
如图①所示,在边长为1的正方形网格中,连接格点D,N和E,C,DN和EC相交于点P,求tan∠CPN的值.
方法归纳
求一个锐角的三角函数值,我们往往需要找出(或构造出)一个直角三角形观察发现问题中∠CPN不在直角三角形中,我们常常利用网格画平行线等方法解决此类问题,比如连接格点M,N,可得MN∥EC,则∠DNM=∠CPN,连接DM,那么∠CPN就变换到Rt△DMN中.
问题解决
(1)直接写出图①中tan∠CPN的值:__________;
(2)如图②,在边长为1的正方形网格中,AN与CM相交于点P,求cos∠CPN的值;
思维拓展
(3)如图③,AB⊥BC,AB=4BC,点M在AB上,且AM=BC,延长CB到N,使BN=2BC,连接AN交CM的延长线于点P,用上述方法构造网格求∠CPN的度数.
参考答案
1.D
2.C
3.A
4.
6.A
7.C
8.A
9.B
10.
11.A
12.B
13.D
14.D
15.<
16.
17.8
18.
19.解析
由勾股定理,得AB==13,
所以,,.
20.D
21.C
22.C
23.D
24.B
25.D
26.A
27.
28.解析
(1)AB=,CD=.
故分别填2;.
(2)取格点E,连接CE,使CE∥AB,取格点F,连接EF,使得EF⊥CD于点G,连接DE,DF,如图所示.
∵∠EDF=∠EGD=90°,∠GED=∠DEF,∴△DEG∽△FED.
∴,即.
∴EG=,DG=.∴CG=CD-DG=.∴tan∠ECG=.
∵AB∥CE,∴∠a=∠ECG.∴tana=.
29.解析(1)2
(2)如图,取格点D,连接CD,DM.
∵CD∥AN,∴∠CPN=∠DCM.
易知△DCM是等腰直角三角形,∴∠DCM=∠CDM=45°.
∴cos∠CPN=cos∠DCM=.
(3)如图,取格点Q,连接AQ、QN.
∵PC∥NQ,∴∠CPN=∠ANQ.
易知△AQN是等腰直角三角形,∴∠ANQ=∠QAN=45°.
∴∠CPN=45°.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
第二章
直角三角形的边角关系
1
锐角三角函数
知识能力全练
知识点一
正切
1.在Rt△ABC中,∠C=90°,a5,b=12,则tanB的值为(
)
A.
B.
C.
D.
2.如图所示,在△ABC中,AD⊥BC交BC于点D,AD=BD,若AB=4,tanC=,则BC=(
)
A.8
B.8
C.7
D.7
3.如图所示,△ABC的顶点在正方形网格的格点上,则tanA的值为(
)
A.
B.
C.2
D.
4.在Rt△ABC中,∠C=90°,若tanA=,则tanB=___________.
5.在Rt△ABC中,∠C=90°,AC=4
cm,tanB=,求BC、AB的长.
识点二
坡度、坡角
6.如图所示,有一斜坡AB,坡顶B离地面的高度BC为30
m,斜坡的倾斜角是∠BAC,若tan∠BAC=,则此斜坡的水平距离AC为(
)
A.75m
B.50m
C.30m
D.12m
7.下图是大坝的横断面,斜坡AB的坡比i=1:2,斜坡CD的坡比i=1:1,若坡面CD的长度为6米,则斜坡AB的长度为(
)
A.4米
B.6米
C.6米
D.24米
8.下图是某河坝横断面示意图,AC为迎水坡,AB为背水坡,过点A作水平面的垂线AD,垂足为D,BD=2CD,设斜坡AC的坡度为iAC,坡角为∠ACD,斜坡AB的坡度为iAB,坡角为∠ABD,则下列结论正确的是(
)
A.iAC=2iAB
B.∠ACD=2∠ABD
C.2iAC=iAB
D.2∠ACD=∠ABD
9.如图所示,为了测量山坡护坡石坝的坡度(坡面的铅直高度与水平宽度的比称为坡度),把一根长5
m的竹竿AC斜靠在石坝旁,量出竿长1
m处的D点离地面的高度DE=0.6
m,又量得竿底与坝脚的距离AB=3
m,则石坝的坡度为(
)
A.
B.3
C.
D.4
10.下图是一斜坡的横截面,小华沿着斜坡从P处出发,走了13米到达M处,此时在铅垂方向上升了5米,那么该斜坡的坡度i=__________.
知识点三
正弦、余弦
11.在台风来临之前,有关部门用钢管加固树木(如图所示),固定点A离地面的高度AC=m,钢管与地面所成角∠ABC=∠1,那么钢管AB的长为(
)
A.
B.
C.m·cos∠1
D.m·sin∠1
12.在正方形网格中,△ABC的位置如图所示,则cosB的值为(
)
A.
B.
C.
D.
13.如图所示,一块矩形木板ABCD斜靠在墙边(OC⊥OB,点A,B,C,D,O在同一平面内)已知AB=a,AD=b,∠BCO=x,则点A到OC的距离等于(
)
A.asinx+bsinx
B.acosx+bcosx
C.asinx+bcosx
D.acosx+bsinx
14.如图所示,△ABC中,∠C=90°,BC=2AC,则cosA=(
)
A.
B.
C.
D.
15.比较大小:sin81°_______tan47°(填“<”“=”或“>”).
16.如图所示,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为点D,如果BC=3,AC=4,那么cos∠BCD=__________.
17.如图所示,在△ABC中,AB=AC=6,sinB=,则△ABC的面积=__________.
18.如图所示,在矩形ABCD中,AB=6,BC=10,将矩形ABCD沿BE折叠,点A落在A′处,若EA′的延长线恰好过点C,则sin∠ABE的值为__________.
19.如图所示,在Rt△ABC中,∠C=90°,BC=5,AC=12,求∠A的正弦值、余弦值
和正切值.
巩固提高全练
20.在Rt△ABC中,∠C=90°,tanA=,则cosA等于(
)
A.
B.
C.
D.
21.sin30°,cos16°,cos43°之间的大小关系是(
)
A.cos43°>cos16°>sin30°
B.cos16°>sin30°>cos43°
C.cos16°>cos43°>sin30°
D.cos43°>sin30°>cos16°
22.如图所示,在Rt△ABC中,CD是斜边AB上的中线,已知CD=2,AC=3,则sinB的值是(
)
A.
B.
C.
D.
23.如图所示,△ABC的三个顶点均在格点上,则cosA的值为(
)
A.
B.
C.2
D.
24.如图所示,为了测量一条河流的宽度,一测量员在河岸边相距200米的P,Q两点分别测定对岸一棵树T的位置,T在P的正北方向,且T在Q的北偏西70°方向,则河宽(PT的长)可以表示为(
)
A.200tan70°米
B.米
C.200sin70°米
D.米
25.如图所示,在4×5的正方形网格中,每个小正方形的边长都是1,△ABC的顶点都在这些小正方形的顶点上,那么sin∠ACB的值为(
)
A.
B.
C.
D.
26.如图所示,矩形ABCD的四个顶点分别在直线3,4,2,1上若直线1∥2∥3∥4且间距相等,AB=4,BC=3,则tana的值为(
)
A.
B.
C.
D.
27.如图所示,点C在线段AB上,且AC=2BC,分别以AC,BC为边在线段AB的同侧作正方形ACDE,BCFG,连接EC,EG,则tan∠CEG=____________.
28.如图所示,在4×4的网格中,每个小正方形的边长为1,线段AB、CD的端点均为格点.
(1)AB的长度为__________,CD的长度为___________;
(2)若AB与CD所夹锐角为aα,求tana的值.
29.问题呈现
如图①所示,在边长为1的正方形网格中,连接格点D,N和E,C,DN和EC相交于点P,求tan∠CPN的值.
方法归纳
求一个锐角的三角函数值,我们往往需要找出(或构造出)一个直角三角形观察发现问题中∠CPN不在直角三角形中,我们常常利用网格画平行线等方法解决此类问题,比如连接格点M,N,可得MN∥EC,则∠DNM=∠CPN,连接DM,那么∠CPN就变换到Rt△DMN中.
问题解决
(1)直接写出图①中tan∠CPN的值:__________;
(2)如图②,在边长为1的正方形网格中,AN与CM相交于点P,求cos∠CPN的值;
思维拓展
(3)如图③,AB⊥BC,AB=4BC,点M在AB上,且AM=BC,延长CB到N,使BN=2BC,连接AN交CM的延长线于点P,用上述方法构造网格求∠CPN的度数.
参考答案
1.D
2.C
3.A
4.
6.A
7.C
8.A
9.B
10.
11.A
12.B
13.D
14.D
15.<
16.
17.8
18.
19.解析
由勾股定理,得AB==13,
所以,,.
20.D
21.C
22.C
23.D
24.B
25.D
26.A
27.
28.解析
(1)AB=,CD=.
故分别填2;.
(2)取格点E,连接CE,使CE∥AB,取格点F,连接EF,使得EF⊥CD于点G,连接DE,DF,如图所示.
∵∠EDF=∠EGD=90°,∠GED=∠DEF,∴△DEG∽△FED.
∴,即.
∴EG=,DG=.∴CG=CD-DG=.∴tan∠ECG=.
∵AB∥CE,∴∠a=∠ECG.∴tana=.
29.解析(1)2
(2)如图,取格点D,连接CD,DM.
∵CD∥AN,∴∠CPN=∠DCM.
易知△DCM是等腰直角三角形,∴∠DCM=∠CDM=45°.
∴cos∠CPN=cos∠DCM=.
(3)如图,取格点Q,连接AQ、QN.
∵PC∥NQ,∴∠CPN=∠ANQ.
易知△AQN是等腰直角三角形,∴∠ANQ=∠QAN=45°.
∴∠CPN=45°.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
