2021-2022学年沪教新版九年级上册数学《第24章 相似三角形》单元测试卷(word版含解析)
文档属性
| 名称 | 2021-2022学年沪教新版九年级上册数学《第24章 相似三角形》单元测试卷(word版含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 324.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-16 13:44:29 | ||
图片预览




文档简介
2021-2022学年沪教新版九年级上册数学《第24章
相似三角形》单元测试卷
一.选择题
1.已知△ABC在正方形网格中的位置如图所示,则点P叫做△ABC的( )
A.中心
B.重心
C.外心
D.内心
2.下列图形中,是相似形的是( )
A.所有平行四边形
B.所有矩形
C.所有菱形
D.所有正方形
3.如图所示的网格由边长相同的小正方形组成,点A、B、C、D、E、F、G在小正方形的顶点上,则△ABC的重心是( )
A.点D
B.点E
C.点F
D.点G
4.已知=,则代数式的值为( )
A.
B.
C.
D.
5.若mn=ab,则下列比例式中不正确的是( )
A.
B.
C.
D.
6.若,则的值为( )
A.
B.﹣1
C.1
D.
7.如果C是线段AB的黄金分割点,并且AC>CB,AB=1,那么AC的长度为( )
A.
B.
C.
D.
8.如图,已知在Rt△ABC中,∠C=90°,AC=BC,AB=6,点P是Rt△ABC的重心,则点P到AB所在直线的距离等于( )
A.1
B.
C.
D.2
9.下列图形中,一定相似的是( )
A.两个正方形
B.两个菱形
C.两个直角三角形
D.两个等腰三角形
10.下列两个图形,一定相似的是( )
A.两个等腰三角形
B.两个直角三角形
C.两个等边三角形
D.两个矩形
二.填空题
11.如图,在△ABC中,D、E分别是BC,AC的中点,AD与BE相交于点G,若DG=1,则AD=
.
12.如图,用放大镜将图形放大,应属于哪一种变换:
(请选填:对称变换、平移变换、旋转变换、相似变换).
13.请指出图中从图1到图2的变换是
变换.
14.某课外活动小组的同学在研究某种植物标本(如图所示)时,测得叶片①最大宽度是8cm,最大长度是16cm;叶片②最大宽度是7cm,最大长度是14cm;叶片③最大宽度约为6.5cm,请你用所学数学知识估算叶片③的完整叶片的最大长度,结果约为
cm.
15.已知,则=
.
16.美是一种感觉,当人体下半身长与身高的比值越接近0.618时,越给人一种美感.如图,某女士身高165cm,下半身长x与身高l的比值是0.60,为尽可能达到好的效果,她应穿的高跟鞋的高度大约为
cm.
17.如图,点G是△ABC的重心,AG的延长线交BC于点D,过点G作GE∥BC交AC于点E,如果BC=6,那么线段GE的长为
.
18.如图,Rt△ABC中,∠BAC=90°,AB=6,AC=4,G是△ABC重心,则S△AGC=
.
19.若=,则=
.
20.在比例尺为1:2000的地图上,测得A、B两地间的图上距离为4.5厘米,则其实际距离为
米.
三.解答题
21.已知,且2x+3y﹣z=18,求4x+y﹣3z的值.
22.若=,求的值.
23.如图,我们规定菱形与正方形,矩形与正方形的接近程度称为“接近度”,在研究“接近度”时,应保证相似图形的“接近度”相等.
(1)设菱形相邻两个内角的度数分别为α°,β°,将菱形的“接近度”定义为|α﹣β|,于是|α﹣β|越小,菱形越接近正方形.
①若菱形的一个内角为80°,则该菱形的“接近度”为
;
②当菱形的“接近度”等于
时,菱形是正方形;
(2)设矩形的长和宽分别为m,n(m≤n),试写出矩形的“接近度”的合理定义.
24.三角形三条边上的中线交于一点,这个点叫三角形的重心.如图G是△ABC的重心.求证:AD=3GD.
25.如图,已知AD是△ABC的中线,G是重心.
(1)设=,=,用向量、表示;
(2)如果AB=3,AC=2,∠GAC=∠GCA,求BG的长.
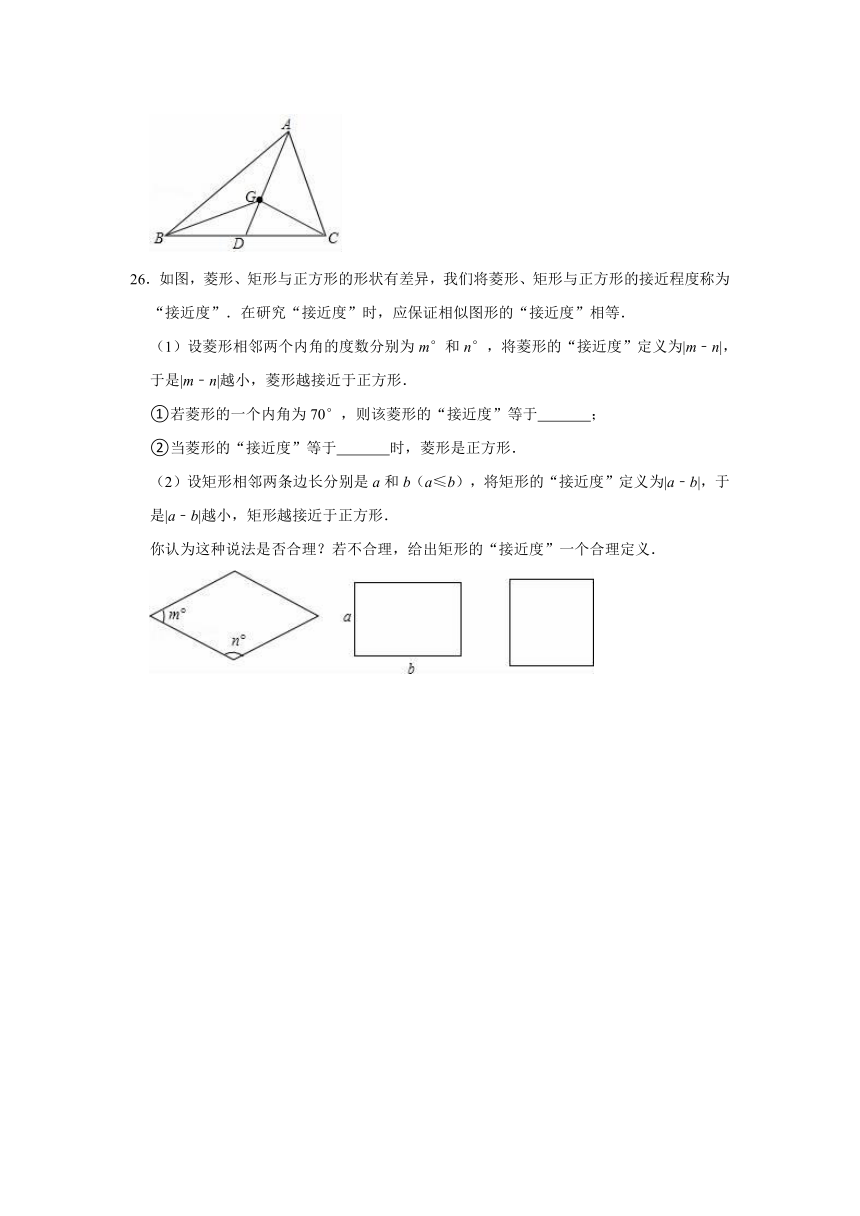
26.如图,菱形、矩形与正方形的形状有差异,我们将菱形、矩形与正方形的接近程度称为“接近度”.在研究“接近度”时,应保证相似图形的“接近度”相等.
(1)设菱形相邻两个内角的度数分别为m°和n°,将菱形的“接近度”定义为|m﹣n|,于是|m﹣n|越小,菱形越接近于正方形.
①若菱形的一个内角为70°,则该菱形的“接近度”等于
;
②当菱形的“接近度”等于
时,菱形是正方形.
(2)设矩形相邻两条边长分别是a和b(a≤b),将矩形的“接近度”定义为|a﹣b|,于是|a﹣b|越小,矩形越接近于正方形.
你认为这种说法是否合理?若不合理,给出矩形的“接近度”一个合理定义.
参考答案与试题解析
一.选择题
1.解:A、等边三角形才有中心,故此选项不合题意;
B、三角形的重心是三角形的三条中线的交点,故此选项符合题意;
C、三角形的外心是三角形的三条垂直平分线的交点,故此选项不合题意;
D、三角形的内心是三角形的三条角平分线的交点,故此选项不合题意.
故选:B.
2.解:A、所有平行四边形,属于形状不唯一确定的图形,不一定相似,故错误;
B、所有矩形,属于形状不唯一确定的图形,不一定相似,故错误;
C、所有菱形,属于形状不唯一确定的图形,不一定相似,故错误;
D、所有正方形,形状相同,但大小不一定相同,符合相似定义,故正确.
故选:D.
3.解:根据题意可知,直线CD经过△ABC的AB边上的中线,直线AD经过△ABC的BC边上的中线,
∴点D是△ABC重心.
故选:A.
4.解:由=得到:a=b,则
==.
故选:B.
5.解:A、由=得,mn=ab,故本选项错误;
B、由=得,mn=ab,故本选项错误;
C、由=得,mb=an,故本选项正确;
D、由=得,mn=ab,故本选项错误.
故选:C.
6.解:由,
得2x=x﹣y,
∴x=﹣y,
∴=﹣1,
故选:B.
7.解:∵C是线段AB的黄金分割点,AC>CB,
∴AC=AB=,
故选:C.
8.解:连接CP并延长,交AB于D,
∵P是Rt△ABC的重心,
∴CD是△ABC的中线,PD=CD,
∵∠C=90°,
∴CD=AB=3,
∵AC=BC,CD是△ABC的中线,
∴CD⊥AB,
∴PD=1,即点P到AB所在直线的距离等于1,
故选:A.
9.解:A、两个正方形角都是直角一定相等,四条边都相等一定成比例,所以一定相似,故本选项正确;
B、两个菱形的对应边成比例,角不一定相等,所以不一定相似,故本选项错误;
C、两个直角三角形的边不一定成比例,角不一定相等,所以不一定相似,故本选项错误;
D、两个等腰三角形的边不一定成比例,角不一定相等,所以不一定相似,故本选项错误.
故选:A.
10.解:∵两个等边三角形的内角都是60°,
∴两个等边三角形一定相似,
故选:C.
二.填空题
11.解:∵D、E分别是BC,AC的中点,
∴点G为△ABC的重心,
∴AG=2DG=2,
∴AD=AG+DG=2+1=3.
故答案为3.
12.解:由一个图形到另一个图形,在改变的过程中形状不变,大小产生变化,属于相似变化.
13.解:∵从图1到图2,图形形状没变,只是大小发生改变,
∴从图1到图2的变换是相似变换.
故答案为:相似,
14.解:根据叶片①②的最大长度和宽度,可得出这种植物的叶片的最大宽度:最大长度=1:2.由此可得出完整的叶片③的最大长度应是6.5×2=13cm.
故答案为:13.
15.解:由题意,设x=5k,y=3k,
∴==.
故答案为:.
16.解:根据已知条件得下半身长是165×0.6=99cm,
设需要穿的高跟鞋是ycm,则根据黄金分割的定义得:,
解得:y≈7.8cm.
故答案为7.8.
17.解:∵点G是△ABC重心,BC=6,
∴CD=BC=3,=2,
∵GE∥BC,
∴△AEG∽△ACD,
∴==,
∴GE=2.
故答案为:2.
18.解:延长AG交BC于E.
∵∠BAC=90°,AB=6,AC=4,
∴S△ABC=?AB?AC=12,
∵G是△ABC的重心,
∴AG=2GE,BE=EC,
∴S△AEC=×12=6,
∴S△AGC=×S△AEC=4,
故答案为4.
19.解:∵=,
∴y=x,
∴==.
故答案为:.
20.解:设A,B两地的实际距离为xcm,则:
1:2000=4.5:x,
解得x=9000.
9000cm=90m.
故答案为:90.
三.解答题
21.解:设=k,
可得:x=2k,y=3k,z=4k,
把x=2k,y=3k,z=4k代入2x+3y﹣z=18中,
可得:4k+9k﹣4k=18,
解得:k=2,
所以x=4,y=6,z=8,
把x=4,y=6,z=8代入4x+y﹣3z=16+6﹣24=﹣2.
22.解:x=2k,y=3k,
==﹣5;
故答案为:﹣5.
23.解:(1)①∵内角为80°,
∴与它相邻内角的度数为100°.
∴菱形的“接近度”=|m﹣n|=|100﹣80|=20.
②当菱形的“接近度”等于0时,菱形是正方形.
故答案为:20;0;
(2)设矩形的长和宽分别为m,n(m≤n),如矩形的“接近度”的定义为,
越接近1,矩形越接近于正方形;
越大,矩形与正方形的形状差异越大;
当=1时,矩形就变成了正方形,即只有矩形的越接近1,矩形才越接近正方形.
24.证明:连接DE,
∵点G是△ABC的重心,
∴点E和点D分别是AB和BC的中点,
∴DE是△ABC的中位线,
∴DE∥AC且DE=AC,
∴△DEG∽△ACG,
∴,
∴,
∴,
∴AD=3DG,
即AD=3GD.
25.解:(1)∵AD是△ABC的中线,=,
∴=,
∵=,
∴=+,
∵G是重心,
∴=×(+)═+;
(2)延长BG交AC于H,
∵∠GAC=∠GCA,
∴GA=GC,
∵G是重心,AC=2,
∴AH=AC=1,
∴BH⊥AC,
在Rt△ABH中,∠AHB=90°,AB=3,
∴BH==2,
∴BG=BH=.
26.解:(1)①∵内角为70°,
∴与它相邻内角的度数为110°.
∴菱形的“接近度”=|m﹣n|=|110﹣70|=40.
②当菱形的“接近度”等于0时,菱形是正方形.
(2)不合理.
例如,对两个相似而不全等的矩形来说,它们接近正方形的程度是相同的,但|a﹣b|却不相等.
合理定义方法不唯一.
如定义为,
越接近1,矩形越接近于正方形;
越大,矩形与正方形的形状差异越大;
当时,矩形就变成了正方形,即只有矩形的越接近1,矩形才越接近正方形.
相似三角形》单元测试卷
一.选择题
1.已知△ABC在正方形网格中的位置如图所示,则点P叫做△ABC的( )
A.中心
B.重心
C.外心
D.内心
2.下列图形中,是相似形的是( )
A.所有平行四边形
B.所有矩形
C.所有菱形
D.所有正方形
3.如图所示的网格由边长相同的小正方形组成,点A、B、C、D、E、F、G在小正方形的顶点上,则△ABC的重心是( )
A.点D
B.点E
C.点F
D.点G
4.已知=,则代数式的值为( )
A.
B.
C.
D.
5.若mn=ab,则下列比例式中不正确的是( )
A.
B.
C.
D.
6.若,则的值为( )
A.
B.﹣1
C.1
D.
7.如果C是线段AB的黄金分割点,并且AC>CB,AB=1,那么AC的长度为( )
A.
B.
C.
D.
8.如图,已知在Rt△ABC中,∠C=90°,AC=BC,AB=6,点P是Rt△ABC的重心,则点P到AB所在直线的距离等于( )
A.1
B.
C.
D.2
9.下列图形中,一定相似的是( )
A.两个正方形
B.两个菱形
C.两个直角三角形
D.两个等腰三角形
10.下列两个图形,一定相似的是( )
A.两个等腰三角形
B.两个直角三角形
C.两个等边三角形
D.两个矩形
二.填空题
11.如图,在△ABC中,D、E分别是BC,AC的中点,AD与BE相交于点G,若DG=1,则AD=
.
12.如图,用放大镜将图形放大,应属于哪一种变换:
(请选填:对称变换、平移变换、旋转变换、相似变换).
13.请指出图中从图1到图2的变换是
变换.
14.某课外活动小组的同学在研究某种植物标本(如图所示)时,测得叶片①最大宽度是8cm,最大长度是16cm;叶片②最大宽度是7cm,最大长度是14cm;叶片③最大宽度约为6.5cm,请你用所学数学知识估算叶片③的完整叶片的最大长度,结果约为
cm.
15.已知,则=
.
16.美是一种感觉,当人体下半身长与身高的比值越接近0.618时,越给人一种美感.如图,某女士身高165cm,下半身长x与身高l的比值是0.60,为尽可能达到好的效果,她应穿的高跟鞋的高度大约为
cm.
17.如图,点G是△ABC的重心,AG的延长线交BC于点D,过点G作GE∥BC交AC于点E,如果BC=6,那么线段GE的长为
.
18.如图,Rt△ABC中,∠BAC=90°,AB=6,AC=4,G是△ABC重心,则S△AGC=
.
19.若=,则=
.
20.在比例尺为1:2000的地图上,测得A、B两地间的图上距离为4.5厘米,则其实际距离为
米.
三.解答题
21.已知,且2x+3y﹣z=18,求4x+y﹣3z的值.
22.若=,求的值.
23.如图,我们规定菱形与正方形,矩形与正方形的接近程度称为“接近度”,在研究“接近度”时,应保证相似图形的“接近度”相等.
(1)设菱形相邻两个内角的度数分别为α°,β°,将菱形的“接近度”定义为|α﹣β|,于是|α﹣β|越小,菱形越接近正方形.
①若菱形的一个内角为80°,则该菱形的“接近度”为
;
②当菱形的“接近度”等于
时,菱形是正方形;
(2)设矩形的长和宽分别为m,n(m≤n),试写出矩形的“接近度”的合理定义.
24.三角形三条边上的中线交于一点,这个点叫三角形的重心.如图G是△ABC的重心.求证:AD=3GD.
25.如图,已知AD是△ABC的中线,G是重心.
(1)设=,=,用向量、表示;
(2)如果AB=3,AC=2,∠GAC=∠GCA,求BG的长.
26.如图,菱形、矩形与正方形的形状有差异,我们将菱形、矩形与正方形的接近程度称为“接近度”.在研究“接近度”时,应保证相似图形的“接近度”相等.
(1)设菱形相邻两个内角的度数分别为m°和n°,将菱形的“接近度”定义为|m﹣n|,于是|m﹣n|越小,菱形越接近于正方形.
①若菱形的一个内角为70°,则该菱形的“接近度”等于
;
②当菱形的“接近度”等于
时,菱形是正方形.
(2)设矩形相邻两条边长分别是a和b(a≤b),将矩形的“接近度”定义为|a﹣b|,于是|a﹣b|越小,矩形越接近于正方形.
你认为这种说法是否合理?若不合理,给出矩形的“接近度”一个合理定义.
参考答案与试题解析
一.选择题
1.解:A、等边三角形才有中心,故此选项不合题意;
B、三角形的重心是三角形的三条中线的交点,故此选项符合题意;
C、三角形的外心是三角形的三条垂直平分线的交点,故此选项不合题意;
D、三角形的内心是三角形的三条角平分线的交点,故此选项不合题意.
故选:B.
2.解:A、所有平行四边形,属于形状不唯一确定的图形,不一定相似,故错误;
B、所有矩形,属于形状不唯一确定的图形,不一定相似,故错误;
C、所有菱形,属于形状不唯一确定的图形,不一定相似,故错误;
D、所有正方形,形状相同,但大小不一定相同,符合相似定义,故正确.
故选:D.
3.解:根据题意可知,直线CD经过△ABC的AB边上的中线,直线AD经过△ABC的BC边上的中线,
∴点D是△ABC重心.
故选:A.
4.解:由=得到:a=b,则
==.
故选:B.
5.解:A、由=得,mn=ab,故本选项错误;
B、由=得,mn=ab,故本选项错误;
C、由=得,mb=an,故本选项正确;
D、由=得,mn=ab,故本选项错误.
故选:C.
6.解:由,
得2x=x﹣y,
∴x=﹣y,
∴=﹣1,
故选:B.
7.解:∵C是线段AB的黄金分割点,AC>CB,
∴AC=AB=,
故选:C.
8.解:连接CP并延长,交AB于D,
∵P是Rt△ABC的重心,
∴CD是△ABC的中线,PD=CD,
∵∠C=90°,
∴CD=AB=3,
∵AC=BC,CD是△ABC的中线,
∴CD⊥AB,
∴PD=1,即点P到AB所在直线的距离等于1,
故选:A.
9.解:A、两个正方形角都是直角一定相等,四条边都相等一定成比例,所以一定相似,故本选项正确;
B、两个菱形的对应边成比例,角不一定相等,所以不一定相似,故本选项错误;
C、两个直角三角形的边不一定成比例,角不一定相等,所以不一定相似,故本选项错误;
D、两个等腰三角形的边不一定成比例,角不一定相等,所以不一定相似,故本选项错误.
故选:A.
10.解:∵两个等边三角形的内角都是60°,
∴两个等边三角形一定相似,
故选:C.
二.填空题
11.解:∵D、E分别是BC,AC的中点,
∴点G为△ABC的重心,
∴AG=2DG=2,
∴AD=AG+DG=2+1=3.
故答案为3.
12.解:由一个图形到另一个图形,在改变的过程中形状不变,大小产生变化,属于相似变化.
13.解:∵从图1到图2,图形形状没变,只是大小发生改变,
∴从图1到图2的变换是相似变换.
故答案为:相似,
14.解:根据叶片①②的最大长度和宽度,可得出这种植物的叶片的最大宽度:最大长度=1:2.由此可得出完整的叶片③的最大长度应是6.5×2=13cm.
故答案为:13.
15.解:由题意,设x=5k,y=3k,
∴==.
故答案为:.
16.解:根据已知条件得下半身长是165×0.6=99cm,
设需要穿的高跟鞋是ycm,则根据黄金分割的定义得:,
解得:y≈7.8cm.
故答案为7.8.
17.解:∵点G是△ABC重心,BC=6,
∴CD=BC=3,=2,
∵GE∥BC,
∴△AEG∽△ACD,
∴==,
∴GE=2.
故答案为:2.
18.解:延长AG交BC于E.
∵∠BAC=90°,AB=6,AC=4,
∴S△ABC=?AB?AC=12,
∵G是△ABC的重心,
∴AG=2GE,BE=EC,
∴S△AEC=×12=6,
∴S△AGC=×S△AEC=4,
故答案为4.
19.解:∵=,
∴y=x,
∴==.
故答案为:.
20.解:设A,B两地的实际距离为xcm,则:
1:2000=4.5:x,
解得x=9000.
9000cm=90m.
故答案为:90.
三.解答题
21.解:设=k,
可得:x=2k,y=3k,z=4k,
把x=2k,y=3k,z=4k代入2x+3y﹣z=18中,
可得:4k+9k﹣4k=18,
解得:k=2,
所以x=4,y=6,z=8,
把x=4,y=6,z=8代入4x+y﹣3z=16+6﹣24=﹣2.
22.解:x=2k,y=3k,
==﹣5;
故答案为:﹣5.
23.解:(1)①∵内角为80°,
∴与它相邻内角的度数为100°.
∴菱形的“接近度”=|m﹣n|=|100﹣80|=20.
②当菱形的“接近度”等于0时,菱形是正方形.
故答案为:20;0;
(2)设矩形的长和宽分别为m,n(m≤n),如矩形的“接近度”的定义为,
越接近1,矩形越接近于正方形;
越大,矩形与正方形的形状差异越大;
当=1时,矩形就变成了正方形,即只有矩形的越接近1,矩形才越接近正方形.
24.证明:连接DE,
∵点G是△ABC的重心,
∴点E和点D分别是AB和BC的中点,
∴DE是△ABC的中位线,
∴DE∥AC且DE=AC,
∴△DEG∽△ACG,
∴,
∴,
∴,
∴AD=3DG,
即AD=3GD.
25.解:(1)∵AD是△ABC的中线,=,
∴=,
∵=,
∴=+,
∵G是重心,
∴=×(+)═+;
(2)延长BG交AC于H,
∵∠GAC=∠GCA,
∴GA=GC,
∵G是重心,AC=2,
∴AH=AC=1,
∴BH⊥AC,
在Rt△ABH中,∠AHB=90°,AB=3,
∴BH==2,
∴BG=BH=.
26.解:(1)①∵内角为70°,
∴与它相邻内角的度数为110°.
∴菱形的“接近度”=|m﹣n|=|110﹣70|=40.
②当菱形的“接近度”等于0时,菱形是正方形.
(2)不合理.
例如,对两个相似而不全等的矩形来说,它们接近正方形的程度是相同的,但|a﹣b|却不相等.
合理定义方法不唯一.
如定义为,
越接近1,矩形越接近于正方形;
越大,矩形与正方形的形状差异越大;
当时,矩形就变成了正方形,即只有矩形的越接近1,矩形才越接近正方形.
