1.2.1对应、映射和函数_课件-湘教版必修1(27张PPT)
文档属性
| 名称 | 1.2.1对应、映射和函数_课件-湘教版必修1(27张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 26.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-16 00:00:00 | ||
图片预览








文档简介
对应、映射和函数
映射的定义:设A,B是两个_____的集合,如果按照某种对应法则f,对于集合A中的任何一个元素,在集合B中都有_____元素和它对应,这样的对应叫作从集合A到集合B的_____ ,记作_________.
在映射f:A→B中,集合A叫作映射的________ ,与A中元素x对应的B中的元素y叫x的___ (image),记作y=f(x)G,x叫作y的_____(inverse image).
自学导引
1.
非空
唯一
映射
f:A→B
定义域
象
原象
如果在某个变化过程中有两个变量x,y,对于每一个在一定范围内变化着的__________________的值,按照一定的对应法则,都有一个_________的y值与之对应,那么,就说y是自变量x的_____,而自变量x的上述变化范围,就叫作该函数的_______ (domain),和自变量x对应的y的值,叫作_______,函数值的变化范围叫作该函数的_____ (co?domain).
函数的定义:设A,B是两个非空的_____,如果按照某种对应法则f,对于集合A中的任何一个数x,在集合B中都有_____的数y和它对应,这样的对应f叫作定义于A取值于B的_____ (function),记作f:A→B,或者_______ (x∈A,y∈B).
2.
3.
自变量(argument)x
唯一确定
函数
定义域
函数值
值域
数集
唯一
函数
y=f(x)
这里,A叫作函数的_______,与x∈A对应的数y叫x的____,记作y=f(x),由所有x∈A的象组成的集合叫作函数的
_____.
观察实际例子并对照定义看出,一个函数f(x)有三个要素:
首先是________ ,也就是如何从x确定f(x)的法则.不知道________ ,就不能从根本上了解这个函数.
其次是______,就是自变量x的取值范围.对应法则形式上相同的两个函数,若______不同,就算不同的函数.
知道了对应法则和定义域,_____也就确定了,对_____的了解表明对函数有了更深入的认识,所以_____也算是函数的要素之一.
4.
定义域
象
值域
对应法则
对应法则
定义域
定义域
值域
值域
值域
函数与映射的主要联系和区别是什么?
提示 函数是一个特殊的映射,函数是非空数集A到非空数集B的映射;而对于映射而言,A和B不一定是数集.
f(x)与f(a)的含义有什么不同?
提示 f(x)是自变量x的函数,在一般情况下是一个变量;f(a)表示当x=a时所得的函数值,是一个常量,f(a)是f(x)的一个特殊值,如:函数f(x)=3x+2,f(2)=3×2+2=8.
自主探究
1.
2.
下列从集合A到集合B的对应f是映射的是( )。
A.A={-1,0,1},B={-1,0,1},f:A中的数平方
B.A={0,1},B={-1,0,1},f:A中的数开方
C.A=Z,B=Q,f:A中的数的倒数
D.A=R,B={正实数},f:A中的数取绝对值
答案 A
预习测评
1.
解析 答案A中的两函数定义域不同,答案B中的两函数值域不同,答案D中的两函数对应法则不同,答案C正确.
答案 C
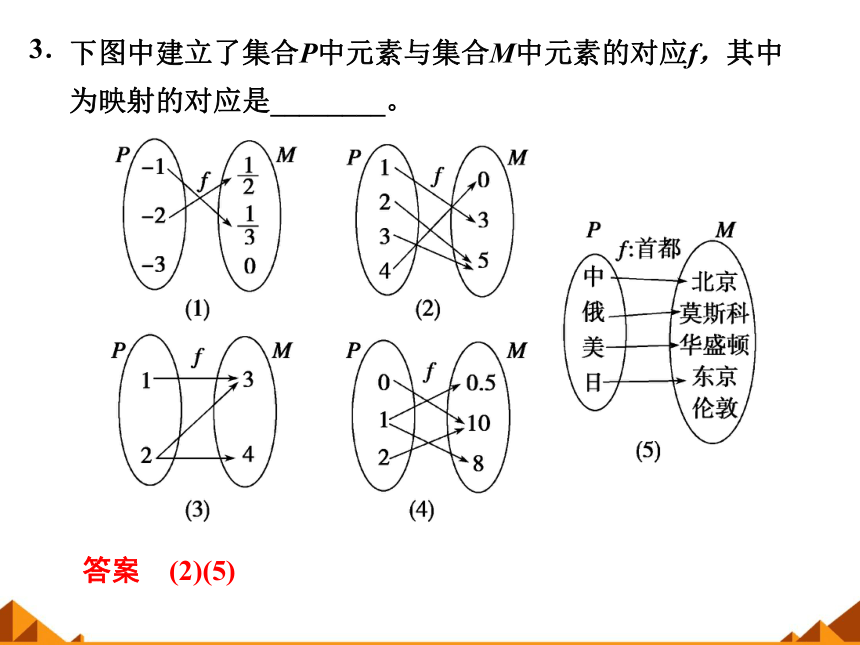
下图中建立了集合P中元素与集合M中元素的对应f,其中为映射的对应是________。
答案 (2)(5)
3.
给出下列四个对应关系,能构成函数的有________(填序号)。
①A=N+,B=Z,f:x→y=2x-3;
②A={1,2,3,4,5,6},B={y|y∈N,y≤5},
f:x→y=|x-1|;
③A={x|x≥2},B={y|y=x2-4x+3},f:x→y=x-3;
④A=N+,B={y∈N+|y=2x,x∈N+},f:x→y=2x-1.
答案 ①②③
4.
对映射概念的理解
(1)“任意”:就是说映射作用下集合A中的每一个元素在集合B中都有它的象,这是映射的完备性。
(2)“集合A到集合B”:映射定义中的两个集合A,B是有先后次序的,A到B的映射与B到A的映射一般是截然不同的,这是映射的方向性。
(3)“有一个且仅有一个”:就是说映射作用下集合A中的任何一个元素在集合B中的象是存在且唯一的,这是映射的存在性与唯一性。
名师点睛
1.
(4)“在B中”:就是说集合A中元素的象必在集合B中,即A中元素的象集是B的子集,这是映射的封闭性。
(5)映射的三要素是集合A、B以及对应法则f,缺一不可;映射不是只有集合A或者集合B,而是集合A、B以及对应法则f的整体,是一个系统,记作f:A→B.有时,映射f:A→B,集合A中的元素a对应集合B中的元素b,也可表示为f:a→b=f(a)或者直接写成b=f(a)。只要其中一个要素不同就是不同的映射。
(6)在一个映射中,集合A、B可以是数集,也可以是点集或其他集合;集合A、B也可以是同一集合。但在确定的映射中,集合A、B的地位一般是不要求对等的。
函数符号y=f(x)的理解
(1)对应法则f是表示定义域和值域的一种对应关系,与所选择的字母无关.在研究函数时,除用符号f(x)外,还常用g(x),F(x),G(x)等符号来表示。变量也不是用唯一的字母来表示,f(x)=x+1与f(t)=t+1是同一个函数。
(2)符号y=f(x)是“y是x的函数”的数学表示,应理解为:x是自变量,它是对应法则所施加的对象;f是对应法则,它既可以是解析式,也可以是图象、表格或文字描述等。y=f(x)仅仅是函数符号,不能认为“y等于f与x的乘积”。
2.
(3)虽然f(x)=x2和f(x-1)=x2等号右边的表达式都是x2,但是,由于对应法则f所施加的对象不同(一个为x,而另一个为x-1),因此函数的解析式是不同的。
(4)f(a)(a是常量)与f(x)的关系:f(a)表示当x=a时,函数f(x)的值,是一个常量;而f(x)是自变量x的函数,一般表示的是变量。
题型一 映射定义的理解
【例1】
典例剖析
解 (1)任一个x都有两个y与之对应,∴不是映射。
(2)对于A中任意一个非负数都有唯一的元素1和它对应,对于A中任意的一个负数都有唯一的元素0和它对应,∴是映射。
(3)在f的作用下,A中的0,1,2,9分别对应到B中的1,0,1,64,
∴是映射。
点评 判断一个对应是不是映射,应该从两个角度去分析:(1)是否是“对于A中的每一个元素”;(2)在B中是否“有唯一的元素与之对应”。
一个对应是映射必须是这两个方面都具备;一个对应对于这两点若有一点不具备就不是映射。
说明一个对应不是映射,只需举一个反例即可。
【变式1】
解 (1)当x=-1时,y的值不存在,
∴不是映射,更不是函数。
(2)是映射,也是函数,因A中所有的元素的倒数都是B中的元素。
(3)∵当A中的元素不为零时,B中有两个元素与之对应,所以不是映射,更不是函数。
(4)是映射,但不是函数,因为A,B不是数集。
已知A={a,b,c},B={-2,0,2},映射f:A→B满足f(a)+f(b)=f(c).求满足条件的映射的个数。
解 (1)当A中三个元素都对应0时,则f(a)+f(b)=0+0=0=f(c)有一个映射;
(2)当A中三个元素对应B中两个时,满足f(a)+f(b)=f(c)的映射有4个,分别为2+0=2,0+2=2,
(-2)+0=-2,0+(-2)=-2
(3)当A中的三个元素对应B中三个元素时,有两个映射,分别为(-2)+2=0,2+(-2)=0
因此满足条件的映射共有7个。
点评 求解含有附加条件的映射问题,必须按映射的定义处理,必要时进行分类讨论。
题型二 映射综合问题
【例2】
【变式2】
(2)x→y,这里y2=x,x∈N,y∈R;
(3)集合A=R,B={-1,1},对应关系f:当x为有理数时,f(x)=-1;当x为无理数时,f(x)=1,该对应是不是从A到B的函数?
题型三 对函数定义的理解
【例3】
(2)当x=4时,y2=4,得y=2或y=-2,不是有唯一值和x对应,所以,x→y(y2=x)不是函数。
(3)是函数,满足函数的定义,在A中任取一个值,B中有唯一确定的值和它对应。
点评 1.判断函数的标准可以简记成:两个非空数集A、B,一个对应关系f,A中任一对B中唯一(即多对一或一对一).
2.函数是一种特殊的对应,要检验给定两个变量之间是否具有函数关系,只要检验:
(1)变量x的取值集合和两变量x、y的对应关系是否给出;
(2)根据给出的对应关系,自变量x在其取值集合中的每一个值,是否都有唯一确定的值y与之对应。
(3)g(x)=x,两者的定义域和对应关系相同,故是同一函数。
(4)f(x)的定义域为(-∞,2)∪(2,+∞),g(x)的定义域为R,故不是同一函数。
【变式3】
[错解] 函数的定义域为R,即k2x2+3kx+1≠0对任意的实数x恒成立,∴Δ=9k2-4k2<0,此时5k2<0,无解,∴k值不存在.
错因分析 本题忽视了k=0的讨论,误认为f(x)=k2x2+3kx+1一定是二次函数。
误区警示 因求函数定义域忽视对二次项系数的讨论而出错
【例4】
纠错心得 求函数的定义域,关键是依据含自变量x的代数式有意义来列出相应的不等式求解,如开偶次方根,被开方数一定是非负数.本题中k2x2+3kx+1≠0应注意二次项系数k2的讨论,不可掉以轻心。
映射的定义
(1)从A到B的映射与从B到A的映射是不同的;确定一个映射需要三个条件:两个非空集合A和B,建立一个对应法则f:A→B,且满足映射的对应关系。
(2)映射有三种对应关系:一是“多对一”,二是“一对一”,再是“一对多”。根据映射的定义可以得知,只有“多对一”和“一对一”才能构成两个非空集合之间的映射,而“一对多”不可以。
(3)映射的定义涉及两个集合A、B,它们可以是数集,也可以是点集或其他的集合。
课堂总结
1.
函数符号y=f(x)是难以理解的抽象符号,它的内涵是“对于定义域中的任意x,在对应关系f的作用下即可得到唯一确定的值y”。在学习过程中,不容易认识到函数概念的整体性,而将函数单一地理解成函数中的对应关系,甚至认为函数就是函数值。
正确理解函数的三要素,其中对应关系是函数的核心,而函数的定义域就是指能使这个解析式有意义的所有实数的集合,在实际问题中,还必须考虑自变量的取值应符合实际意义。
2.
3.
映射的定义:设A,B是两个_____的集合,如果按照某种对应法则f,对于集合A中的任何一个元素,在集合B中都有_____元素和它对应,这样的对应叫作从集合A到集合B的_____ ,记作_________.
在映射f:A→B中,集合A叫作映射的________ ,与A中元素x对应的B中的元素y叫x的___ (image),记作y=f(x)G,x叫作y的_____(inverse image).
自学导引
1.
非空
唯一
映射
f:A→B
定义域
象
原象
如果在某个变化过程中有两个变量x,y,对于每一个在一定范围内变化着的__________________的值,按照一定的对应法则,都有一个_________的y值与之对应,那么,就说y是自变量x的_____,而自变量x的上述变化范围,就叫作该函数的_______ (domain),和自变量x对应的y的值,叫作_______,函数值的变化范围叫作该函数的_____ (co?domain).
函数的定义:设A,B是两个非空的_____,如果按照某种对应法则f,对于集合A中的任何一个数x,在集合B中都有_____的数y和它对应,这样的对应f叫作定义于A取值于B的_____ (function),记作f:A→B,或者_______ (x∈A,y∈B).
2.
3.
自变量(argument)x
唯一确定
函数
定义域
函数值
值域
数集
唯一
函数
y=f(x)
这里,A叫作函数的_______,与x∈A对应的数y叫x的____,记作y=f(x),由所有x∈A的象组成的集合叫作函数的
_____.
观察实际例子并对照定义看出,一个函数f(x)有三个要素:
首先是________ ,也就是如何从x确定f(x)的法则.不知道________ ,就不能从根本上了解这个函数.
其次是______,就是自变量x的取值范围.对应法则形式上相同的两个函数,若______不同,就算不同的函数.
知道了对应法则和定义域,_____也就确定了,对_____的了解表明对函数有了更深入的认识,所以_____也算是函数的要素之一.
4.
定义域
象
值域
对应法则
对应法则
定义域
定义域
值域
值域
值域
函数与映射的主要联系和区别是什么?
提示 函数是一个特殊的映射,函数是非空数集A到非空数集B的映射;而对于映射而言,A和B不一定是数集.
f(x)与f(a)的含义有什么不同?
提示 f(x)是自变量x的函数,在一般情况下是一个变量;f(a)表示当x=a时所得的函数值,是一个常量,f(a)是f(x)的一个特殊值,如:函数f(x)=3x+2,f(2)=3×2+2=8.
自主探究
1.
2.
下列从集合A到集合B的对应f是映射的是( )。
A.A={-1,0,1},B={-1,0,1},f:A中的数平方
B.A={0,1},B={-1,0,1},f:A中的数开方
C.A=Z,B=Q,f:A中的数的倒数
D.A=R,B={正实数},f:A中的数取绝对值
答案 A
预习测评
1.
解析 答案A中的两函数定义域不同,答案B中的两函数值域不同,答案D中的两函数对应法则不同,答案C正确.
答案 C
下图中建立了集合P中元素与集合M中元素的对应f,其中为映射的对应是________。
答案 (2)(5)
3.
给出下列四个对应关系,能构成函数的有________(填序号)。
①A=N+,B=Z,f:x→y=2x-3;
②A={1,2,3,4,5,6},B={y|y∈N,y≤5},
f:x→y=|x-1|;
③A={x|x≥2},B={y|y=x2-4x+3},f:x→y=x-3;
④A=N+,B={y∈N+|y=2x,x∈N+},f:x→y=2x-1.
答案 ①②③
4.
对映射概念的理解
(1)“任意”:就是说映射作用下集合A中的每一个元素在集合B中都有它的象,这是映射的完备性。
(2)“集合A到集合B”:映射定义中的两个集合A,B是有先后次序的,A到B的映射与B到A的映射一般是截然不同的,这是映射的方向性。
(3)“有一个且仅有一个”:就是说映射作用下集合A中的任何一个元素在集合B中的象是存在且唯一的,这是映射的存在性与唯一性。
名师点睛
1.
(4)“在B中”:就是说集合A中元素的象必在集合B中,即A中元素的象集是B的子集,这是映射的封闭性。
(5)映射的三要素是集合A、B以及对应法则f,缺一不可;映射不是只有集合A或者集合B,而是集合A、B以及对应法则f的整体,是一个系统,记作f:A→B.有时,映射f:A→B,集合A中的元素a对应集合B中的元素b,也可表示为f:a→b=f(a)或者直接写成b=f(a)。只要其中一个要素不同就是不同的映射。
(6)在一个映射中,集合A、B可以是数集,也可以是点集或其他集合;集合A、B也可以是同一集合。但在确定的映射中,集合A、B的地位一般是不要求对等的。
函数符号y=f(x)的理解
(1)对应法则f是表示定义域和值域的一种对应关系,与所选择的字母无关.在研究函数时,除用符号f(x)外,还常用g(x),F(x),G(x)等符号来表示。变量也不是用唯一的字母来表示,f(x)=x+1与f(t)=t+1是同一个函数。
(2)符号y=f(x)是“y是x的函数”的数学表示,应理解为:x是自变量,它是对应法则所施加的对象;f是对应法则,它既可以是解析式,也可以是图象、表格或文字描述等。y=f(x)仅仅是函数符号,不能认为“y等于f与x的乘积”。
2.
(3)虽然f(x)=x2和f(x-1)=x2等号右边的表达式都是x2,但是,由于对应法则f所施加的对象不同(一个为x,而另一个为x-1),因此函数的解析式是不同的。
(4)f(a)(a是常量)与f(x)的关系:f(a)表示当x=a时,函数f(x)的值,是一个常量;而f(x)是自变量x的函数,一般表示的是变量。
题型一 映射定义的理解
【例1】
典例剖析
解 (1)任一个x都有两个y与之对应,∴不是映射。
(2)对于A中任意一个非负数都有唯一的元素1和它对应,对于A中任意的一个负数都有唯一的元素0和它对应,∴是映射。
(3)在f的作用下,A中的0,1,2,9分别对应到B中的1,0,1,64,
∴是映射。
点评 判断一个对应是不是映射,应该从两个角度去分析:(1)是否是“对于A中的每一个元素”;(2)在B中是否“有唯一的元素与之对应”。
一个对应是映射必须是这两个方面都具备;一个对应对于这两点若有一点不具备就不是映射。
说明一个对应不是映射,只需举一个反例即可。
【变式1】
解 (1)当x=-1时,y的值不存在,
∴不是映射,更不是函数。
(2)是映射,也是函数,因A中所有的元素的倒数都是B中的元素。
(3)∵当A中的元素不为零时,B中有两个元素与之对应,所以不是映射,更不是函数。
(4)是映射,但不是函数,因为A,B不是数集。
已知A={a,b,c},B={-2,0,2},映射f:A→B满足f(a)+f(b)=f(c).求满足条件的映射的个数。
解 (1)当A中三个元素都对应0时,则f(a)+f(b)=0+0=0=f(c)有一个映射;
(2)当A中三个元素对应B中两个时,满足f(a)+f(b)=f(c)的映射有4个,分别为2+0=2,0+2=2,
(-2)+0=-2,0+(-2)=-2
(3)当A中的三个元素对应B中三个元素时,有两个映射,分别为(-2)+2=0,2+(-2)=0
因此满足条件的映射共有7个。
点评 求解含有附加条件的映射问题,必须按映射的定义处理,必要时进行分类讨论。
题型二 映射综合问题
【例2】
【变式2】
(2)x→y,这里y2=x,x∈N,y∈R;
(3)集合A=R,B={-1,1},对应关系f:当x为有理数时,f(x)=-1;当x为无理数时,f(x)=1,该对应是不是从A到B的函数?
题型三 对函数定义的理解
【例3】
(2)当x=4时,y2=4,得y=2或y=-2,不是有唯一值和x对应,所以,x→y(y2=x)不是函数。
(3)是函数,满足函数的定义,在A中任取一个值,B中有唯一确定的值和它对应。
点评 1.判断函数的标准可以简记成:两个非空数集A、B,一个对应关系f,A中任一对B中唯一(即多对一或一对一).
2.函数是一种特殊的对应,要检验给定两个变量之间是否具有函数关系,只要检验:
(1)变量x的取值集合和两变量x、y的对应关系是否给出;
(2)根据给出的对应关系,自变量x在其取值集合中的每一个值,是否都有唯一确定的值y与之对应。
(3)g(x)=x,两者的定义域和对应关系相同,故是同一函数。
(4)f(x)的定义域为(-∞,2)∪(2,+∞),g(x)的定义域为R,故不是同一函数。
【变式3】
[错解] 函数的定义域为R,即k2x2+3kx+1≠0对任意的实数x恒成立,∴Δ=9k2-4k2<0,此时5k2<0,无解,∴k值不存在.
错因分析 本题忽视了k=0的讨论,误认为f(x)=k2x2+3kx+1一定是二次函数。
误区警示 因求函数定义域忽视对二次项系数的讨论而出错
【例4】
纠错心得 求函数的定义域,关键是依据含自变量x的代数式有意义来列出相应的不等式求解,如开偶次方根,被开方数一定是非负数.本题中k2x2+3kx+1≠0应注意二次项系数k2的讨论,不可掉以轻心。
映射的定义
(1)从A到B的映射与从B到A的映射是不同的;确定一个映射需要三个条件:两个非空集合A和B,建立一个对应法则f:A→B,且满足映射的对应关系。
(2)映射有三种对应关系:一是“多对一”,二是“一对一”,再是“一对多”。根据映射的定义可以得知,只有“多对一”和“一对一”才能构成两个非空集合之间的映射,而“一对多”不可以。
(3)映射的定义涉及两个集合A、B,它们可以是数集,也可以是点集或其他的集合。
课堂总结
1.
函数符号y=f(x)是难以理解的抽象符号,它的内涵是“对于定义域中的任意x,在对应关系f的作用下即可得到唯一确定的值y”。在学习过程中,不容易认识到函数概念的整体性,而将函数单一地理解成函数中的对应关系,甚至认为函数就是函数值。
正确理解函数的三要素,其中对应关系是函数的核心,而函数的定义域就是指能使这个解析式有意义的所有实数的集合,在实际问题中,还必须考虑自变量的取值应符合实际意义。
2.
3.
