2.5.2形形色色的函数模型_课件-湘教版必修1(40张PPT)
文档属性
| 名称 | 2.5.2形形色色的函数模型_课件-湘教版必修1(40张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-16 00:00:00 | ||
图片预览











文档简介
几种函数增长快慢的比较
形形色色的函数模型
结合实例体会直线上升、指数爆炸、对数增长等不同增长的函数模型意义,理解它们的增长差异性.
能够借助信息技术,利用函数图象及数据表格,对几种常见增长类型的函数的增长状况进行比较,初步体会它们的增长差异性;收集一些社会生活中普遍使用的函数模型
(指数函数、对数函数、幂函数、分段函数等),了解函数模型的广泛应用.
能够合理地把实际问题转化为数学问题,将文字语言转化为数学语言,用数学知识建立相应的数学模型.
【课标要求】
1.
2.
3.
递增函数的共同特点是,函数值y随着自变量x的增长而_____ ,同为增长,但增长的_____可能不同.
函数赛跑,自变量好比是_____ ,函数值就像是跑的_____ .要比就比同样的自变量对应的_______ ,让自变量_______时定胜负.
指数增长最___,对数增长最___.
函数快慢的比较,还可以看_____的变化,看它是越跑越快呢,还是越跑越慢.
自学导引
1.
2.
增长
快慢
时间
路程
函数值
充分大
快
速度
慢
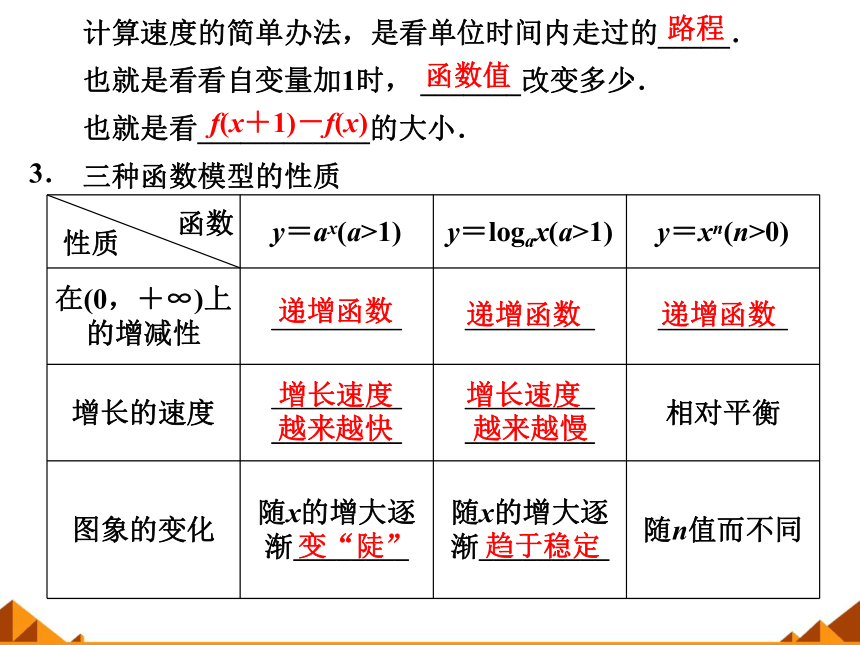
计算速度的简单办法,是看单位时间内走过的_____.
也就是看看自变量加1时, _______改变多少.
也就是看____________的大小.
三种函数模型的性质
路程
函数值
f(x+1)-f(x)
3.
y=ax(a>1)
y=logax(a>1)
y=xn(n>0)
在(0,+∞)上的增减性
_________
_________
_________
增长的速度
_________
_________
_________
_________
相对平衡
图象的变化
随x的增大逐渐________
随x的增大逐渐_________
随n值而不同
递增函数
递增函数
递增函数
增长速度
越来越快
增长速度
越来越慢
变“陡”
趋于稳定
函数
性质
指数函数y=ax(a>1),对数函数y=logax(a>1)和幂函数y=xn(n>0)增长速度的比较:
(1)对于指数函数y=ax和幂函数y=xn(n>0),在区间(0,+∞)上,无论n比a大多少,尽管在x的一定范围内,ax会小于xn,但由于_____的增长快于_____的增长,因此总存在一个x0,当x>x0时,就会有_____ ;
(2)对于对数函数y=logax(a>1)和幂函数y=xn(n>0),在区间(0,+∞)上,尽管在x的一定范围内,logax可能会大于xn,但由于________的增长慢于_____的增长,因此总存在一个x0,当x>x0时,就会有________.
4.
y=ax
y=xn
ax>xn
y=logax
y=xn
logax比较模拟函数的优劣,既要考虑到_____最小,又要考虑生产的_____问题,比如增产的趋势和可能性.
把现实世界中的实际问题加以提炼,抽象为_________ ,求出模型的___,验证模型的______,并用该数学模型所提供的解答来解释_________ ,数学知识的这一应用过程称为
_________ .
对于现实中的实际模型,适当作出一些必要的简化和假设,运用适当的数学工具得到一个数学结构.也可以说,数学建模是
利用_________(符号、式子与图象)模拟现实的原型,把现实
原型___________为某种数学结构是数学模型的基本特征.它
或者能解释特定现象的现实状态,或者能预测到对象的未来状
况,或者能提供处理对象的最优决策或控制方案.
5.
6.
误差
实际
数学模型
解
合理性
现实问题
数学建模
数学语言
抽象、简化
数学建模的步骤通常是:
(1)正确理解并简化_________:了解问题的实际背景,明确其实际意义,掌握对象的各种信息.
根据实际对象的特征和建模的目的,对问题进行必要的_____,并用精确的语言提出一些恰当的假设.
(2)建立_________ :在(1)的基础上,利用适当的数学工具来刻画各变量之间的数学关系,建立相应的_________ .
(3)求得数学问题的___.
?(4)将数学模型分析计算的_____与实际情形进行比较,验证模型的_____性、_____性和_____性.
7.
实际问题
简化
数学模型
数学结构
解
结果
准确
合理
适用
函数y=x2与y=2x在(0,+∞)上具有相同的增长速度吗?
提示 增长速度不同.如图所示,在(0,2)之间y=x2的增长速度较快,在(2,4)之间函数值均从4增大到16,而x=4之后,y=2x的增长速度远远快于y=x2的增长速度.
自主探究
1.
数据拟合时,得到的函数为什么需要检验?
提示 因为根据已给的数据,作出散点图,根据散点图,一般是从我们比较熟悉的最简单的函数作模拟,但所估计的函数有时可能误差较大或不切合客观实际,此时就要再改选其他函数模型.
2.
答案 A
预习测评
我国工农业总产值从1980年到2000年的20年间翻两番,设平均每年的增长率为x,则有 ( ).
A.(1+x)19=4 B.(1+x)20=3
C.(1+x)20=2 D.(1+x)20=4
解析 设1980年总产值为a,则有a(1+x)20=2×(2a),即(1+x)20=4.
答案 D
国家规定的个人稿酬纳税办法是:不超过800元不纳税,超过800元不超过4 000元的按超过800元的14%纳税,超过4 000元的按全部稿酬的11%纳税,某人出版了一本书,共纳税420元,他的稿费为________元.
解析 ∵3 000×14%=420(元),∴他的稿费应为3 800元.
答案 3 800
2.
3.
一商品零售价2011年比2010年上涨了25%,欲控制2012年比2010年上涨10%,则2012年应比2011年降价______%.
答案 12
4.
三类不同增长函数的综合运用
指数函数、对数函数以及幂函数是描述客观变化规律的重要数学模型.比如价格与利润、成本与收入、纳税、交通安全、人口等问题都可以借助函数模型来解决.
建立数学模型是解决数学问题的主要方法,数学建模一般分为识模、析模、建模、解模、验模五个步骤.识模就是把应用问题的外部信息和自己已有的内部经验相对照,初步判断问题解决的方向;析模就是精读问题,做到“咬文嚼
名师点睛
1.
字”,抓住关键词,化简转换问题,注意已知量,发现未知量,挖掘隐含量;建模是通过数学符号化,把问题转化为数学模型的过程;解模时我们可以借助计算机等数学工具对所建模型求解;由于应用问题本身的繁杂性、开放性,根据自己理解所建立的模型也有局限性,最后要对模型的解检验,或取或舍,或重新修正模型,直到满意为止.
解答函数应用题应注意的问题
首先,要认真阅读理解材料:应用题所用的数学语言多为“文字语言、符号语言、图形语言”,往往篇幅较长,立意有创新脱俗之感觉.阅读理解材料要达到的目标是:读懂题目所叙述的实际问题的意义,领悟其中的数学本质,接受题目所约定的临时性定义,理解题目中的量与量的位置关系、数量关
2.
系,确立解题思路和下一步的努力方向,对于有些数量关系较复杂、较模糊的问题,可以借助画图和列表来理清它.
其次,建立函数关系:根据前面的审题及分析,把实际问题“用字母符号、关系符号”表达出来,建立函数关系.
按复利计算本利和(或利息)的一种储蓄,本金为a元,每期利率为r,设本利和为y,存期为x,写出本利和y随存期x变化的函数式.如果存入本金1 000元,每期利率2.25%,试计算5期后的本利和是多少?
解 已知本金为a元.
1期后的本利和为y1=a+a×r=a(1+r);
2期后的本利和为y2=a(1+r)+a(1+r)r=a(1+r)2;
3期后的本利和为y3=a(1+r)3;
……
x期后的本利和为y=a(1+r)x.
题型一 指数或对数型函数
【例1】
典例剖析
将a=1 000(元),r=2.25%,x=5代入上式得
y=1 000×(1+2.25%)5=1 000×1.022 55.
由计算器算得y=1 117.68(元).
∴复利函数式为y=a(1+r)x,5期后的本利和为1 117.68元.
点评 复利是一种计算利息的方法,即把前一期的利息和本金加在一起做本金,再计算下一期的利息,其实质是指数函数的应用.
【变式1】
某地西红柿从2月1日起开始上市.通过市场调查,得到西红柿种植成本Q(单位:元/102 kg)与上市时间t(单位:天)的数据如下表:
题型二 函数模型的选择问题
【例2】
时间/t
50
110
250
种植成本/Q
150
108
150
(1)根据上表数据,从下列函数中选取一个函数描述西红柿种植成本Q与上市时间t的变化关系:Q=at+b,Q=at2+bt+c,Q=a·bt,Q=a·logbt;
(2)利用你选取的函数,求西红柿种植成本最低时的上市天数及最低种植成本.
解 (1)由提供的数据知道,描述西红柿种植成本Q与上市时间t的变化关系的函数不可能是常数函数,从而用函数Q=at+b,Q=a·bt,Q=a·logbt中的任意一个进行描述时都应有a≠0,而此时上述三个函数均为单调函数,这与表格所提供的数据不符合.所以,选取二次函数Q=at2+bt+c进行描述.
以表格所提供的三组数据分别代入Q=at2+bt+c得到:
点评 此类未知函数模型的问题,解题过程一般为:
(1)作散点图;
(2)选择函数模型:一般是根据散点图的特征,联想哪些函数具有类似的图象特征,找几个比较接近的函数模型尝试;
(3)求出函数模型:求出(2)中找到的几个函数模型的解析式;
(4)检验:将(3)中求出的几个函数模型进行比较、验证,得出最合适的函数模型;
(5)利用所求出的函数模型解决问题.
九十年代,政府间气候变化专业委员会(IPCC)提供的一项报告指出:使全球气候逐年变暖的一个重要因素是人类在能源利用与森林砍伐的过程中使CO2浓度增加.据测,1990年、1991年、1992年大气中的CO2浓度分别比1989年增加了1个可比单位、3个可比单位、6个可比单位.若用一个函数模拟九十年代中每年CO2浓度增加的可比单位数y与年份增加数x的关系,模拟函数可选用二次函数或函数y=abx+c(其中a、b、c为常数),且又知1994年大气中的CO2浓度比1989年增加了16个可比单位,请问用以上哪个函数作为模拟函数较好?
【变式2】
解 若以f(x)=px2+qx+r作为模拟函数,则依题意得
如图所示,在直角坐标系的第一象限内,△AOB是边长为2的等边三角形,设直线x=t(0≤t≤2)截这个三角形可得位于此直线左方的图形的面积为f(t).
(1)求函数f(t)的表达式,并注明定义域;
(2)画出函数f(t)的简图.
题型三 分段函数模型问题
【例3】
图1 图2
(2)f(t)的图象为:
点评 由于分段函数与日常生活联系紧密,已成为考查的热点.对于分段函数,一要注意规范书写格式;二要注意各段的定义域的表示方法,对于中间的各个分点,一般是“一边闭,一边开”,以保证在各分点的“不重不漏”.
某人开汽车以60 km/h速度从A地到150 km远的B地,在B地停留1 h后再以50 km/h的速度返回A地.把汽车离开A地的路程x(km)表示为时间t(h)(从A地出发时计起)的函数,并画函数图象;再把车速v km/h表示为时间t(h)的函数,并画函数图象.
解 汽车离开A地的距离x km与时间t h关系:
【变式3】
图象如图:
速度v km/h与时间t的函数关系式是
图象如图
如图所示,圆弧型声波DFE从坐标原点O点外传播.若D是DFE与x轴的交点,设OD=x(0≤x≤a),圆弧型声波DFE在传播过程中扫过平行四边形OABC的面积为y(图中阴影部分),则函数y=f(x)的图象大致是 ( ).
误区警示 因未理解题意而出错
【例4】
[错解] 观察图可知,声波扫过的面积先增大后减小,故正确答案为B.
错因分析 本题的错误很明显,y指的是声波扫过的总面积,不是发展趋势,所以扫过的面积始终是增大的,上述判断是因主观性太强而致错.
[正解] 从题目所给的背景图形中不难发现:在声波未传到C点之前,扫过图形的面积不断增大,而且增长得越来越快.当到达C点之后且离开A点之前,因为OA∥BC,所以此时扫过图形的面积呈匀速增长.当离开A点之后,扫过图形的面积会增长得越来越慢,所以函数图象刚开始应是下凹的,然后是一条上升的线段,最后是上凸的.故选A.
答案 A
纠错心得 函数图象的凸凹性是函数的一个重要性质,其一般规律是:上凸函数图象若减,则从左到右减得越来越快;若增,则从左到右增得越来越慢;下凹函数图象正好相反.
把实际问题抽象为数学问题,逐步把数学知识应用到生产、生活的实际中去,形成应用数学的意识,是培养学生分析问题、解决问题能力的最终目的.
解答数学应用题的关键有两点:一是认真读题,缜密审题,确切理解题意,明确问题的实际背景,然后进行科学地抽象、概括,将实际问题归纳为相应的数学问题;二是要合理选取参变量,设定变元后,就要寻找它们之间的内在联系,选用恰当的代数式表示问题中的关系,建立相应的函数、方程模型,最终求解数学模型使实际问题解决.
课堂总结
1.
2.
解题过程中究竟选用哪种函数模型,要根据题目具体要求进行抽象和概括,灵活地建立数学模型.常见函数模型有:
①一次函数型模型:y=kx+b(k,b为常数,k≠0);
②二次函数型模型:y=ax2+bx+c(a,b,c为常数,a≠0);
③指数函数型模型:y=abx+c(a,b,c为常数,a≠0,b>0,b≠1);
④对数函数型模型:y=mlogax+n(m,n,a为常数,a>0,a≠1,m≠0);
⑤幂函数型模型:y=axn+b(a,b,n为常数,a≠0,n≠1).
用待定系数法求函数解析式.待定系数法是一种非常重要的数学方法,常首先根据题意,设出函数解析式,取特殊值代入函数解析式得到方程组,由方程组求出待定系数.
3.
4.
根据题意比较所选用的几类函数解析式,选取适合要求的函数.
要熟悉一次函数、二次函数、指数函数、对数函数和幂函数的图象及性质,有助于我们开拓思路,提高运算速度.
解答函数应用题的一般步骤:
第一步:阅读题目中的文字叙述,理解叙述中所反映的实际背景,领悟从背景中概括出来的数学实质.尤其是理解叙述中的新名词、新概念,进而把握住新信息.
在此基础上,分析出已知什么,求什么,涉及哪些知识,确定自变量与函数值的意义.审题时要抓住题目中的关键量,要勇于探究、敏于发现、归纳,善于联想、化归,实现实际问题向数学问题的转化.
5.
6.
7.
第二步:引进数学符号,建立数学模型.
一般地,设自变量为x,函数为y,并用x表示各相关量,然后根据问题已知条件,运用已掌握的数学知识、物理知识及其他相关知识建立函数关系,将实际问题转化为一个数学问题,实现问题的数学化,即所谓建立数学模型.
第三步:利用数学方法将得到的常规数学问题(即数学模型)予以解答,求得结果.
第四步:再转译成具体问题作出解答.
形形色色的函数模型
结合实例体会直线上升、指数爆炸、对数增长等不同增长的函数模型意义,理解它们的增长差异性.
能够借助信息技术,利用函数图象及数据表格,对几种常见增长类型的函数的增长状况进行比较,初步体会它们的增长差异性;收集一些社会生活中普遍使用的函数模型
(指数函数、对数函数、幂函数、分段函数等),了解函数模型的广泛应用.
能够合理地把实际问题转化为数学问题,将文字语言转化为数学语言,用数学知识建立相应的数学模型.
【课标要求】
1.
2.
3.
递增函数的共同特点是,函数值y随着自变量x的增长而_____ ,同为增长,但增长的_____可能不同.
函数赛跑,自变量好比是_____ ,函数值就像是跑的_____ .要比就比同样的自变量对应的_______ ,让自变量_______时定胜负.
指数增长最___,对数增长最___.
函数快慢的比较,还可以看_____的变化,看它是越跑越快呢,还是越跑越慢.
自学导引
1.
2.
增长
快慢
时间
路程
函数值
充分大
快
速度
慢
计算速度的简单办法,是看单位时间内走过的_____.
也就是看看自变量加1时, _______改变多少.
也就是看____________的大小.
三种函数模型的性质
路程
函数值
f(x+1)-f(x)
3.
y=ax(a>1)
y=logax(a>1)
y=xn(n>0)
在(0,+∞)上的增减性
_________
_________
_________
增长的速度
_________
_________
_________
_________
相对平衡
图象的变化
随x的增大逐渐________
随x的增大逐渐_________
随n值而不同
递增函数
递增函数
递增函数
增长速度
越来越快
增长速度
越来越慢
变“陡”
趋于稳定
函数
性质
指数函数y=ax(a>1),对数函数y=logax(a>1)和幂函数y=xn(n>0)增长速度的比较:
(1)对于指数函数y=ax和幂函数y=xn(n>0),在区间(0,+∞)上,无论n比a大多少,尽管在x的一定范围内,ax会小于xn,但由于_____的增长快于_____的增长,因此总存在一个x0,当x>x0时,就会有_____ ;
(2)对于对数函数y=logax(a>1)和幂函数y=xn(n>0),在区间(0,+∞)上,尽管在x的一定范围内,logax可能会大于xn,但由于________的增长慢于_____的增长,因此总存在一个x0,当x>x0时,就会有________.
4.
y=ax
y=xn
ax>xn
y=logax
y=xn
logax
把现实世界中的实际问题加以提炼,抽象为_________ ,求出模型的___,验证模型的______,并用该数学模型所提供的解答来解释_________ ,数学知识的这一应用过程称为
_________ .
对于现实中的实际模型,适当作出一些必要的简化和假设,运用适当的数学工具得到一个数学结构.也可以说,数学建模是
利用_________(符号、式子与图象)模拟现实的原型,把现实
原型___________为某种数学结构是数学模型的基本特征.它
或者能解释特定现象的现实状态,或者能预测到对象的未来状
况,或者能提供处理对象的最优决策或控制方案.
5.
6.
误差
实际
数学模型
解
合理性
现实问题
数学建模
数学语言
抽象、简化
数学建模的步骤通常是:
(1)正确理解并简化_________:了解问题的实际背景,明确其实际意义,掌握对象的各种信息.
根据实际对象的特征和建模的目的,对问题进行必要的_____,并用精确的语言提出一些恰当的假设.
(2)建立_________ :在(1)的基础上,利用适当的数学工具来刻画各变量之间的数学关系,建立相应的_________ .
(3)求得数学问题的___.
?(4)将数学模型分析计算的_____与实际情形进行比较,验证模型的_____性、_____性和_____性.
7.
实际问题
简化
数学模型
数学结构
解
结果
准确
合理
适用
函数y=x2与y=2x在(0,+∞)上具有相同的增长速度吗?
提示 增长速度不同.如图所示,在(0,2)之间y=x2的增长速度较快,在(2,4)之间函数值均从4增大到16,而x=4之后,y=2x的增长速度远远快于y=x2的增长速度.
自主探究
1.
数据拟合时,得到的函数为什么需要检验?
提示 因为根据已给的数据,作出散点图,根据散点图,一般是从我们比较熟悉的最简单的函数作模拟,但所估计的函数有时可能误差较大或不切合客观实际,此时就要再改选其他函数模型.
2.
答案 A
预习测评
我国工农业总产值从1980年到2000年的20年间翻两番,设平均每年的增长率为x,则有 ( ).
A.(1+x)19=4 B.(1+x)20=3
C.(1+x)20=2 D.(1+x)20=4
解析 设1980年总产值为a,则有a(1+x)20=2×(2a),即(1+x)20=4.
答案 D
国家规定的个人稿酬纳税办法是:不超过800元不纳税,超过800元不超过4 000元的按超过800元的14%纳税,超过4 000元的按全部稿酬的11%纳税,某人出版了一本书,共纳税420元,他的稿费为________元.
解析 ∵3 000×14%=420(元),∴他的稿费应为3 800元.
答案 3 800
2.
3.
一商品零售价2011年比2010年上涨了25%,欲控制2012年比2010年上涨10%,则2012年应比2011年降价______%.
答案 12
4.
三类不同增长函数的综合运用
指数函数、对数函数以及幂函数是描述客观变化规律的重要数学模型.比如价格与利润、成本与收入、纳税、交通安全、人口等问题都可以借助函数模型来解决.
建立数学模型是解决数学问题的主要方法,数学建模一般分为识模、析模、建模、解模、验模五个步骤.识模就是把应用问题的外部信息和自己已有的内部经验相对照,初步判断问题解决的方向;析模就是精读问题,做到“咬文嚼
名师点睛
1.
字”,抓住关键词,化简转换问题,注意已知量,发现未知量,挖掘隐含量;建模是通过数学符号化,把问题转化为数学模型的过程;解模时我们可以借助计算机等数学工具对所建模型求解;由于应用问题本身的繁杂性、开放性,根据自己理解所建立的模型也有局限性,最后要对模型的解检验,或取或舍,或重新修正模型,直到满意为止.
解答函数应用题应注意的问题
首先,要认真阅读理解材料:应用题所用的数学语言多为“文字语言、符号语言、图形语言”,往往篇幅较长,立意有创新脱俗之感觉.阅读理解材料要达到的目标是:读懂题目所叙述的实际问题的意义,领悟其中的数学本质,接受题目所约定的临时性定义,理解题目中的量与量的位置关系、数量关
2.
系,确立解题思路和下一步的努力方向,对于有些数量关系较复杂、较模糊的问题,可以借助画图和列表来理清它.
其次,建立函数关系:根据前面的审题及分析,把实际问题“用字母符号、关系符号”表达出来,建立函数关系.
按复利计算本利和(或利息)的一种储蓄,本金为a元,每期利率为r,设本利和为y,存期为x,写出本利和y随存期x变化的函数式.如果存入本金1 000元,每期利率2.25%,试计算5期后的本利和是多少?
解 已知本金为a元.
1期后的本利和为y1=a+a×r=a(1+r);
2期后的本利和为y2=a(1+r)+a(1+r)r=a(1+r)2;
3期后的本利和为y3=a(1+r)3;
……
x期后的本利和为y=a(1+r)x.
题型一 指数或对数型函数
【例1】
典例剖析
将a=1 000(元),r=2.25%,x=5代入上式得
y=1 000×(1+2.25%)5=1 000×1.022 55.
由计算器算得y=1 117.68(元).
∴复利函数式为y=a(1+r)x,5期后的本利和为1 117.68元.
点评 复利是一种计算利息的方法,即把前一期的利息和本金加在一起做本金,再计算下一期的利息,其实质是指数函数的应用.
【变式1】
某地西红柿从2月1日起开始上市.通过市场调查,得到西红柿种植成本Q(单位:元/102 kg)与上市时间t(单位:天)的数据如下表:
题型二 函数模型的选择问题
【例2】
时间/t
50
110
250
种植成本/Q
150
108
150
(1)根据上表数据,从下列函数中选取一个函数描述西红柿种植成本Q与上市时间t的变化关系:Q=at+b,Q=at2+bt+c,Q=a·bt,Q=a·logbt;
(2)利用你选取的函数,求西红柿种植成本最低时的上市天数及最低种植成本.
解 (1)由提供的数据知道,描述西红柿种植成本Q与上市时间t的变化关系的函数不可能是常数函数,从而用函数Q=at+b,Q=a·bt,Q=a·logbt中的任意一个进行描述时都应有a≠0,而此时上述三个函数均为单调函数,这与表格所提供的数据不符合.所以,选取二次函数Q=at2+bt+c进行描述.
以表格所提供的三组数据分别代入Q=at2+bt+c得到:
点评 此类未知函数模型的问题,解题过程一般为:
(1)作散点图;
(2)选择函数模型:一般是根据散点图的特征,联想哪些函数具有类似的图象特征,找几个比较接近的函数模型尝试;
(3)求出函数模型:求出(2)中找到的几个函数模型的解析式;
(4)检验:将(3)中求出的几个函数模型进行比较、验证,得出最合适的函数模型;
(5)利用所求出的函数模型解决问题.
九十年代,政府间气候变化专业委员会(IPCC)提供的一项报告指出:使全球气候逐年变暖的一个重要因素是人类在能源利用与森林砍伐的过程中使CO2浓度增加.据测,1990年、1991年、1992年大气中的CO2浓度分别比1989年增加了1个可比单位、3个可比单位、6个可比单位.若用一个函数模拟九十年代中每年CO2浓度增加的可比单位数y与年份增加数x的关系,模拟函数可选用二次函数或函数y=abx+c(其中a、b、c为常数),且又知1994年大气中的CO2浓度比1989年增加了16个可比单位,请问用以上哪个函数作为模拟函数较好?
【变式2】
解 若以f(x)=px2+qx+r作为模拟函数,则依题意得
如图所示,在直角坐标系的第一象限内,△AOB是边长为2的等边三角形,设直线x=t(0≤t≤2)截这个三角形可得位于此直线左方的图形的面积为f(t).
(1)求函数f(t)的表达式,并注明定义域;
(2)画出函数f(t)的简图.
题型三 分段函数模型问题
【例3】
图1 图2
(2)f(t)的图象为:
点评 由于分段函数与日常生活联系紧密,已成为考查的热点.对于分段函数,一要注意规范书写格式;二要注意各段的定义域的表示方法,对于中间的各个分点,一般是“一边闭,一边开”,以保证在各分点的“不重不漏”.
某人开汽车以60 km/h速度从A地到150 km远的B地,在B地停留1 h后再以50 km/h的速度返回A地.把汽车离开A地的路程x(km)表示为时间t(h)(从A地出发时计起)的函数,并画函数图象;再把车速v km/h表示为时间t(h)的函数,并画函数图象.
解 汽车离开A地的距离x km与时间t h关系:
【变式3】
图象如图:
速度v km/h与时间t的函数关系式是
图象如图
如图所示,圆弧型声波DFE从坐标原点O点外传播.若D是DFE与x轴的交点,设OD=x(0≤x≤a),圆弧型声波DFE在传播过程中扫过平行四边形OABC的面积为y(图中阴影部分),则函数y=f(x)的图象大致是 ( ).
误区警示 因未理解题意而出错
【例4】
[错解] 观察图可知,声波扫过的面积先增大后减小,故正确答案为B.
错因分析 本题的错误很明显,y指的是声波扫过的总面积,不是发展趋势,所以扫过的面积始终是增大的,上述判断是因主观性太强而致错.
[正解] 从题目所给的背景图形中不难发现:在声波未传到C点之前,扫过图形的面积不断增大,而且增长得越来越快.当到达C点之后且离开A点之前,因为OA∥BC,所以此时扫过图形的面积呈匀速增长.当离开A点之后,扫过图形的面积会增长得越来越慢,所以函数图象刚开始应是下凹的,然后是一条上升的线段,最后是上凸的.故选A.
答案 A
纠错心得 函数图象的凸凹性是函数的一个重要性质,其一般规律是:上凸函数图象若减,则从左到右减得越来越快;若增,则从左到右增得越来越慢;下凹函数图象正好相反.
把实际问题抽象为数学问题,逐步把数学知识应用到生产、生活的实际中去,形成应用数学的意识,是培养学生分析问题、解决问题能力的最终目的.
解答数学应用题的关键有两点:一是认真读题,缜密审题,确切理解题意,明确问题的实际背景,然后进行科学地抽象、概括,将实际问题归纳为相应的数学问题;二是要合理选取参变量,设定变元后,就要寻找它们之间的内在联系,选用恰当的代数式表示问题中的关系,建立相应的函数、方程模型,最终求解数学模型使实际问题解决.
课堂总结
1.
2.
解题过程中究竟选用哪种函数模型,要根据题目具体要求进行抽象和概括,灵活地建立数学模型.常见函数模型有:
①一次函数型模型:y=kx+b(k,b为常数,k≠0);
②二次函数型模型:y=ax2+bx+c(a,b,c为常数,a≠0);
③指数函数型模型:y=abx+c(a,b,c为常数,a≠0,b>0,b≠1);
④对数函数型模型:y=mlogax+n(m,n,a为常数,a>0,a≠1,m≠0);
⑤幂函数型模型:y=axn+b(a,b,n为常数,a≠0,n≠1).
用待定系数法求函数解析式.待定系数法是一种非常重要的数学方法,常首先根据题意,设出函数解析式,取特殊值代入函数解析式得到方程组,由方程组求出待定系数.
3.
4.
根据题意比较所选用的几类函数解析式,选取适合要求的函数.
要熟悉一次函数、二次函数、指数函数、对数函数和幂函数的图象及性质,有助于我们开拓思路,提高运算速度.
解答函数应用题的一般步骤:
第一步:阅读题目中的文字叙述,理解叙述中所反映的实际背景,领悟从背景中概括出来的数学实质.尤其是理解叙述中的新名词、新概念,进而把握住新信息.
在此基础上,分析出已知什么,求什么,涉及哪些知识,确定自变量与函数值的意义.审题时要抓住题目中的关键量,要勇于探究、敏于发现、归纳,善于联想、化归,实现实际问题向数学问题的转化.
5.
6.
7.
第二步:引进数学符号,建立数学模型.
一般地,设自变量为x,函数为y,并用x表示各相关量,然后根据问题已知条件,运用已掌握的数学知识、物理知识及其他相关知识建立函数关系,将实际问题转化为一个数学问题,实现问题的数学化,即所谓建立数学模型.
第三步:利用数学方法将得到的常规数学问题(即数学模型)予以解答,求得结果.
第四步:再转译成具体问题作出解答.
