8.3(1)怎样判定三角形全等

(共16张PPT)
京华中学 徐静
（第一课时）
1、通过画图、操作、实验、观察等活动，探索三角形全等的判定方法。
2、了解“ASA,AAS”，并能初步运用它们判定两个三角形全等。
阅读课本28---29页
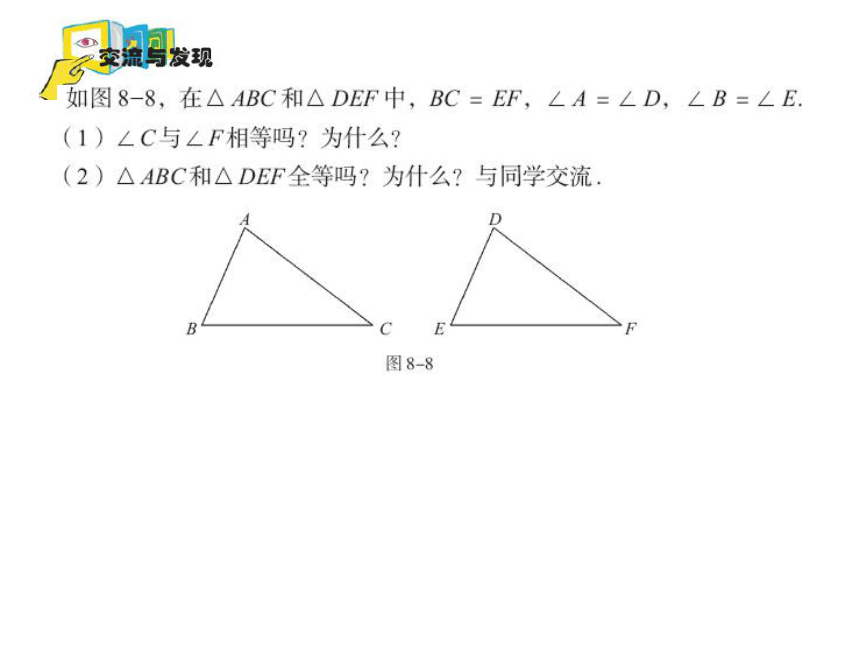
1、如果已知一个三角形的两角及一边，那么有几种可能的情况呢？
2、完成实验与探究
通过上面的实验与探究,你能得到什么结论 与同学交流.
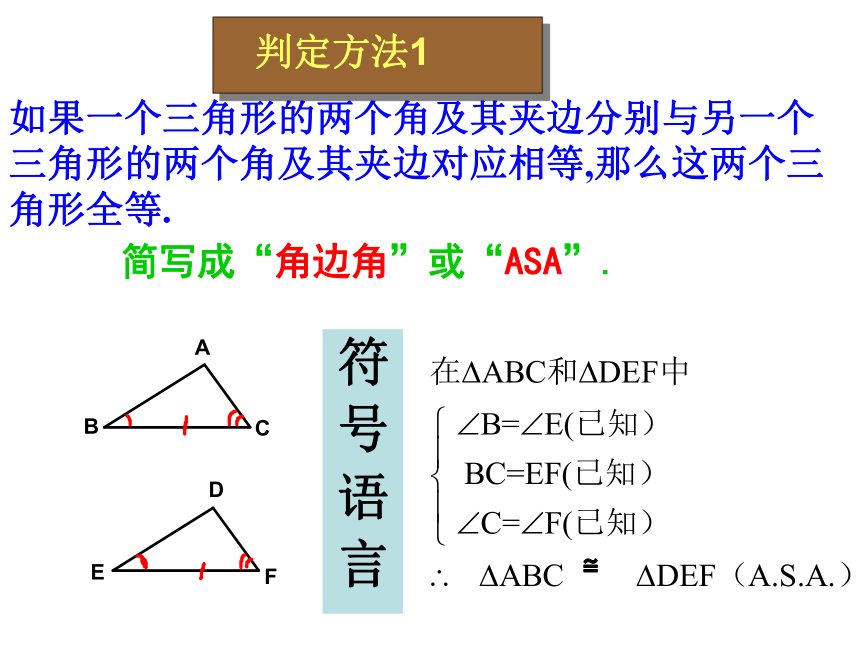
如果一个三角形的两个角及其夹边分别与另一个三角形的两个角及其夹边对应相等,那么这两个三角形全等.
符 号 语 言
≌
判定方法1
简写成“角边角”或“ASA”.
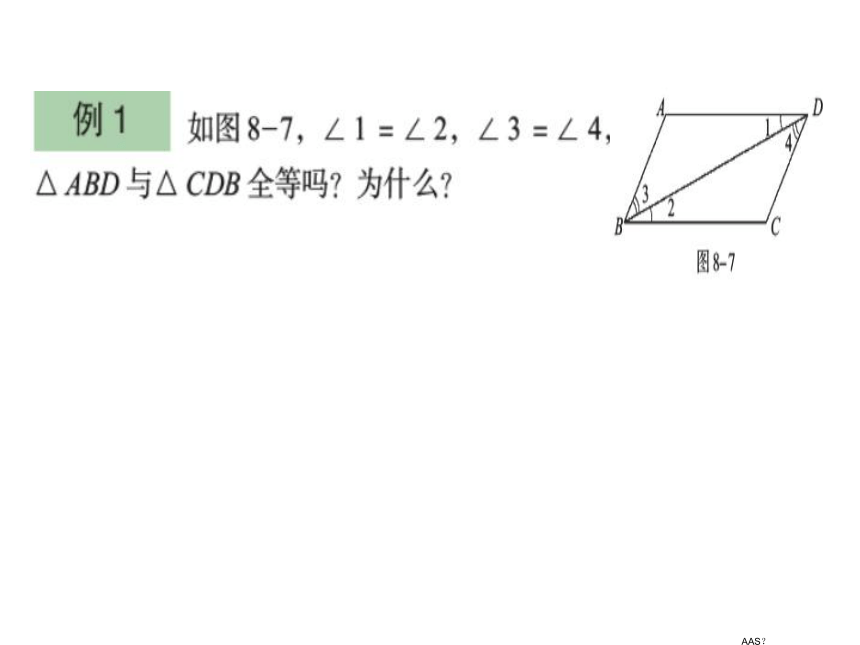
AAS？
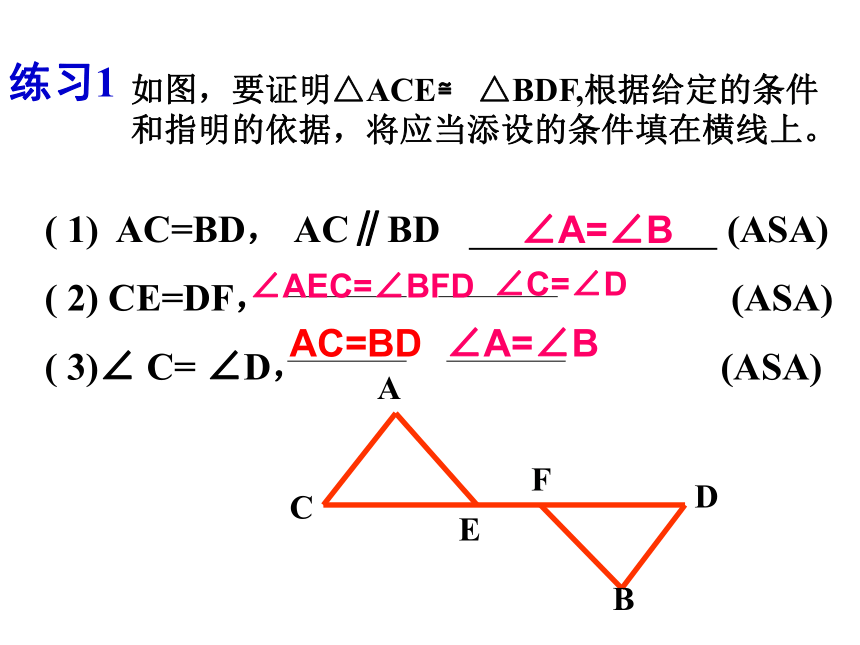
如图，要证明△ACE≌ △BDF,根据给定的条件和指明的依据，将应当添设的条件填在横线上。
( 1) AC=BD， AC∥BD (ASA)
( 2) CE=DF， (ASA)
( 3)∠ C= ∠D， (ASA)
C
B
A
E
F
D
∠AEC=∠BFD
∠A=∠B
∠C=∠D
AC=BD
∠A=∠B
练习1
A
B
C
D
E
F
如果一个三角形的两个角及其中一角的对边分别与另一个三角形的两个角及其中一角的对边对应相等,那么这两个三角形全等.
这个判定方法可以简单地用“角角边” 或“ AAS”来表示.
符 号 语 言
判定方法2
已知：如图，AB＝AC，CE⊥AB于E， BD⊥AC于D，
求证：BD＝CE.
练习2
(角边角)
(角角边)
三角形全等的判定方法
(1) 两角和它们的夹边对应相等的两个三角形全等.
简写成“角边角”或“ASA”.
(2) 两角和其中一角的对边对应相等的两个三角形全等.
简写成“角角边”或“AAS”.
知识要点：
（3）探索三角形全等是证明线段相等（对应边相等），角
相等（对应角相等）等问题的基本途径。
数学思想：
要学会用分类的思想，转化的思想解决问题。
练习册12页1、2、4、5