等比数列
图片预览









文档简介
(共36张PPT)
2.4 等比数列
第一课时
*
教学目标
知识与技能目标
1.等比数列的定义;
2.等比数列的通项公式.
过程与能力目标
1.明确等比数列的定义;
2.掌握等比数列的通项公式,会解决知道公式中的三个元素,求另一个的问题.
教学重点
1.等比数列概念的理解与掌握;
2.等比数列的通项公式的推导及应用.
教学难点
等差数列"等比"的理解、把握和应用.
问题提出
1.什么叫等差数列?其递推公式是什么?
从第2项起,每一项与它的前一项的差等于同一个常数的数列称为等差数列.
或an-1+an+1=2 an(n≥2).
2.就数列的单调性而言,等差数列有哪几种类型?
d>0时,{an}是递增数列;
d<0时,{an}是递减数列;
d=0时,{an}是常数列.
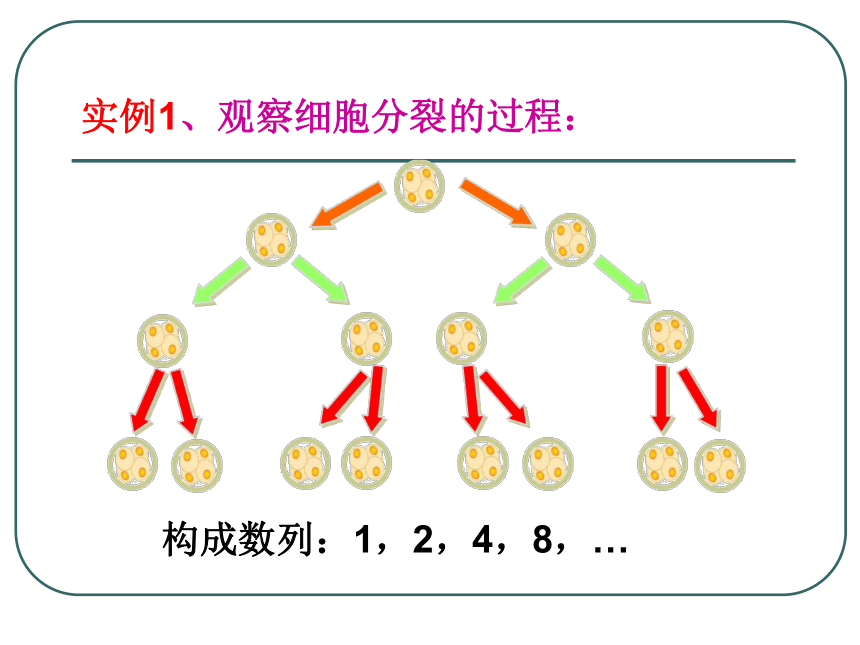
实例1、观察细胞分裂的过程:
构成数列:1,2,4,8,…
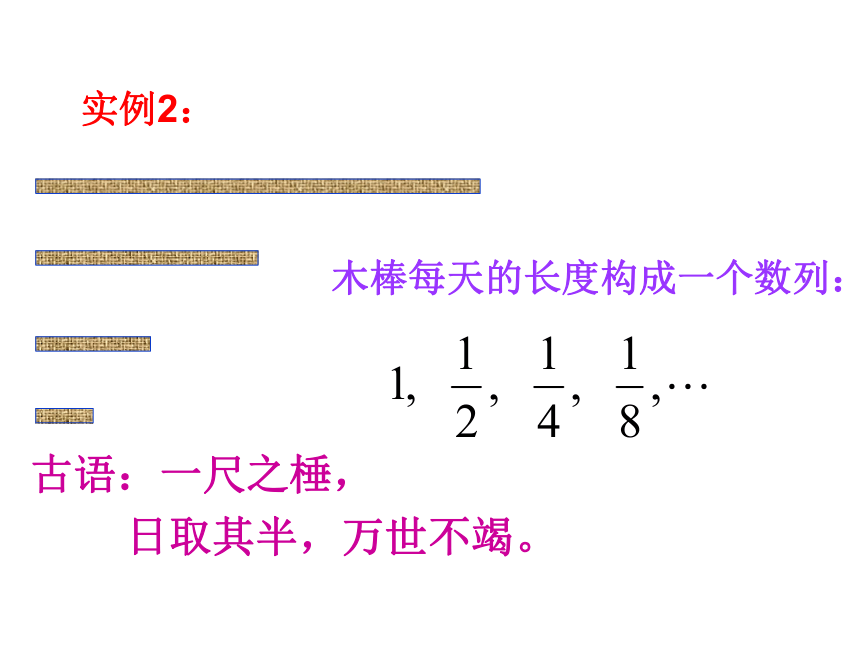
古语:一尺之棰,
日取其半,万世不竭。
木棒每天的长度构成一个数列:
实例2:
实例3:一种计算机病毒通过邮件进行传播,如果把病毒制造者发送病毒称为第一轮,邮件接收者发送病毒称为第二轮,依此类推.假设每一轮每台计算机都感染20台计算机,那么在不重复的情况下,这种病毒每一轮感染的计算机数构成的数列是什么?
1,20,202,203,….
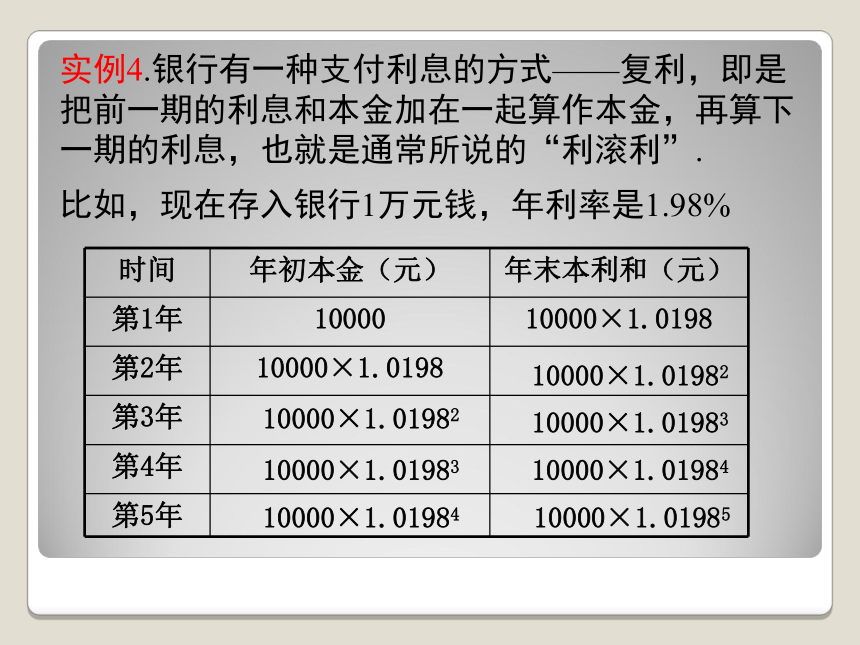
实例4.银行有一种支付利息的方式——复利,即是把前一期的利息和本金加在一起算作本金,再算下一期的利息,也就是通常所说的“利滚利”.
比如,现在存入银行1万元钱,年利率是1.98%
时间 年初本金(元) 年末本利和(元)
第1年 10000 10000×1.0198
第2年 10000×1.0198
第3年
第4年
第5年
10000×1.01982
10000×1.01982
10000×1.01983
10000×1.01983
10000×1.01984
10000×1.01984
10000×1.01985
①1,2,4,8,…
②
③1,20,202,203…
④ 10000×1.01981 , 10000×1.01982 , 10000×1.01983 , 10000×1.01984…
共同特点:从第2项起,每一项与前一项的比都等于同一个常数。
思考:以下数列有什么共同特点?
我们把上述数列都叫做等比数列,你能给出等比数列的一般定义吗?
如果一个数列从第2项起,每一项与它的前一项的比等于同一个常数,这个数列就叫做等比数列,这个常数就叫做等比数列的公比(常用字母q表示).
思考1:等比数列的公比q能取0吗?
×
(4)等比数列的数学语言定义中: 无法用
替代。
对等比数列的认识:
(2)等比数列的每一项都不为0,即 ;
(1)等比数列的首项不为0;
(3)公比不为0.
思考2:公比q<0时,等比数列呈现怎样的特点?
正负交替
对公比q的探究: (a1 ﹥0时)
当0﹤q﹤1时,等比数列{an}为递减数列;
当q﹥1时,等比数列{an}为递增数列;
当q=1时,等比数列{an}为常数列;
当q﹤0时,等比数列{an}为摆动数列。
思考3:有无数列是既等比又等差的?
注意:当 时,数列 既是等差又是等比数列,当 时,它只是等差数列,而不是等比数列.
练习1:课本52页 2
练习2:课本53页 5(1)
知识探究(二):等比数列的通项公式
思考1:下面四个等比数列的通项公式分别是什么?
(1)1,2,4,8,….
(2)1, ….
(3)1,20,202,203,….
(4)1000×1.0198,1000×1.01982,1000×1.01983,1000×1.01984,…
(1)an=
(2) an=
(3)an=
(4) an=
思考2:设等比数列{an}的首项为a1,公比为q,那么a2,a3,a4,a5分别等于什么?由此归纳猜想,an等于什么?
思考3:如何根据等比数列的定义证明上述结论?
(不完全归纳法)
…
q
a
a
1
2
=
2
1
2
3
q
a
q
a
a
=
=
3
1
3
4
q
a
q
a
a
=
=
1
1
1
-
-
=
=
n
n
n
q
a
q
a
a
不完全归纳法
累乘法
等比数列的通项公式
等比数列的通项公式:
an=a1qn-1
(n∈N﹡,q≠0)
特别地,等比数列{an}中,a1≠0,q≠0
m
n
m
q
a
-
=
数 列 等 差 数 列 等 比 数 列
定 义
公差(比)
定义变形
通项公式
一般形式
an+1-an=d
d 叫公差
q叫公比
an+1=an+d
an+1=an q
an= a1+(n-1)d
an=a1qn-1
an=am+(n-m)d
an=amqn-m
思考4:将等比数列的通项公式看作是一个关于n的函数,这是一个什么类型的函数?
思考5: 从通项公式,想象一下等比数列的
图象是怎么样的吗?
o
1
2
3
4
5
6
1
2
3
4
5
6
7
8
等比数列通项公式的图象表示:
课本50页探究(2)
例1.在等比数列 中,
例题讲解
例2 根据下列程序框图,写出所打印数列的前5项,并建立数列的递推公式,求出其通项公式.
开始
输出A
n=n+1
n=1
A=0.5A
n≥5?
否
结束
是
A=1
例3 一个等比数列的第3项和第4项分别是12和18,求它的第1项和第2项.
例4. 已知数列{an}满足
a1=1,an+1=2an+1.
(1)求证数列{an+1}是等比数列;
(2)求{an}的表达式.
思考6:在等比数列{an}中,an-1,an,an+1三者之间有什么关系?
an-1·a n+1 =an2 (n≥2)
观察如下的两个数之间,插入一个什么数后者三个数就会成为一个等比数列:
(1)1, , 9
(2)-1, ,-4
(3)-12, ,-3
(4)1, ,1
±3
±2
±6
±1
等比中项
如果在a与b中间插入一个数G,使 a、G、b成等比数列,那么G叫做a与b的等比中项。
因此,
如果G是a与b的等比中项,那么
,即
小结作业
1.等比数列的基本特征可理解为:从 第2项起,每一项与它的前一项的比都 相等,并且可以用两种递推公式来描述.
2.等比数列的通项公式是由其定义推导出来的,确定一个等比数列需要两个独立条件.
3.等比数列与等差数列是两个并列概念,但二者有很大的差异,根据等比数列的定义和通项公式还可发掘出许多性质,具体内容待后探究.
作业:
P53习题2.4A组:1,2,3 .
2.4 等比数列
第一课时
*
教学目标
知识与技能目标
1.等比数列的定义;
2.等比数列的通项公式.
过程与能力目标
1.明确等比数列的定义;
2.掌握等比数列的通项公式,会解决知道公式中的三个元素,求另一个的问题.
教学重点
1.等比数列概念的理解与掌握;
2.等比数列的通项公式的推导及应用.
教学难点
等差数列"等比"的理解、把握和应用.
问题提出
1.什么叫等差数列?其递推公式是什么?
从第2项起,每一项与它的前一项的差等于同一个常数的数列称为等差数列.
或an-1+an+1=2 an(n≥2).
2.就数列的单调性而言,等差数列有哪几种类型?
d>0时,{an}是递增数列;
d<0时,{an}是递减数列;
d=0时,{an}是常数列.
实例1、观察细胞分裂的过程:
构成数列:1,2,4,8,…
古语:一尺之棰,
日取其半,万世不竭。
木棒每天的长度构成一个数列:
实例2:
实例3:一种计算机病毒通过邮件进行传播,如果把病毒制造者发送病毒称为第一轮,邮件接收者发送病毒称为第二轮,依此类推.假设每一轮每台计算机都感染20台计算机,那么在不重复的情况下,这种病毒每一轮感染的计算机数构成的数列是什么?
1,20,202,203,….
实例4.银行有一种支付利息的方式——复利,即是把前一期的利息和本金加在一起算作本金,再算下一期的利息,也就是通常所说的“利滚利”.
比如,现在存入银行1万元钱,年利率是1.98%
时间 年初本金(元) 年末本利和(元)
第1年 10000 10000×1.0198
第2年 10000×1.0198
第3年
第4年
第5年
10000×1.01982
10000×1.01982
10000×1.01983
10000×1.01983
10000×1.01984
10000×1.01984
10000×1.01985
①1,2,4,8,…
②
③1,20,202,203…
④ 10000×1.01981 , 10000×1.01982 , 10000×1.01983 , 10000×1.01984…
共同特点:从第2项起,每一项与前一项的比都等于同一个常数。
思考:以下数列有什么共同特点?
我们把上述数列都叫做等比数列,你能给出等比数列的一般定义吗?
如果一个数列从第2项起,每一项与它的前一项的比等于同一个常数,这个数列就叫做等比数列,这个常数就叫做等比数列的公比(常用字母q表示).
思考1:等比数列的公比q能取0吗?
×
(4)等比数列的数学语言定义中: 无法用
替代。
对等比数列的认识:
(2)等比数列的每一项都不为0,即 ;
(1)等比数列的首项不为0;
(3)公比不为0.
思考2:公比q<0时,等比数列呈现怎样的特点?
正负交替
对公比q的探究: (a1 ﹥0时)
当0﹤q﹤1时,等比数列{an}为递减数列;
当q﹥1时,等比数列{an}为递增数列;
当q=1时,等比数列{an}为常数列;
当q﹤0时,等比数列{an}为摆动数列。
思考3:有无数列是既等比又等差的?
注意:当 时,数列 既是等差又是等比数列,当 时,它只是等差数列,而不是等比数列.
练习1:课本52页 2
练习2:课本53页 5(1)
知识探究(二):等比数列的通项公式
思考1:下面四个等比数列的通项公式分别是什么?
(1)1,2,4,8,….
(2)1, ….
(3)1,20,202,203,….
(4)1000×1.0198,1000×1.01982,1000×1.01983,1000×1.01984,…
(1)an=
(2) an=
(3)an=
(4) an=
思考2:设等比数列{an}的首项为a1,公比为q,那么a2,a3,a4,a5分别等于什么?由此归纳猜想,an等于什么?
思考3:如何根据等比数列的定义证明上述结论?
(不完全归纳法)
…
q
a
a
1
2
=
2
1
2
3
q
a
q
a
a
=
=
3
1
3
4
q
a
q
a
a
=
=
1
1
1
-
-
=
=
n
n
n
q
a
q
a
a
不完全归纳法
累乘法
等比数列的通项公式
等比数列的通项公式:
an=a1qn-1
(n∈N﹡,q≠0)
特别地,等比数列{an}中,a1≠0,q≠0
m
n
m
q
a
-
=
数 列 等 差 数 列 等 比 数 列
定 义
公差(比)
定义变形
通项公式
一般形式
an+1-an=d
d 叫公差
q叫公比
an+1=an+d
an+1=an q
an= a1+(n-1)d
an=a1qn-1
an=am+(n-m)d
an=amqn-m
思考4:将等比数列的通项公式看作是一个关于n的函数,这是一个什么类型的函数?
思考5: 从通项公式,想象一下等比数列的
图象是怎么样的吗?
o
1
2
3
4
5
6
1
2
3
4
5
6
7
8
等比数列通项公式的图象表示:
课本50页探究(2)
例1.在等比数列 中,
例题讲解
例2 根据下列程序框图,写出所打印数列的前5项,并建立数列的递推公式,求出其通项公式.
开始
输出A
n=n+1
n=1
A=0.5A
n≥5?
否
结束
是
A=1
例3 一个等比数列的第3项和第4项分别是12和18,求它的第1项和第2项.
例4. 已知数列{an}满足
a1=1,an+1=2an+1.
(1)求证数列{an+1}是等比数列;
(2)求{an}的表达式.
思考6:在等比数列{an}中,an-1,an,an+1三者之间有什么关系?
an-1·a n+1 =an2 (n≥2)
观察如下的两个数之间,插入一个什么数后者三个数就会成为一个等比数列:
(1)1, , 9
(2)-1, ,-4
(3)-12, ,-3
(4)1, ,1
±3
±2
±6
±1
等比中项
如果在a与b中间插入一个数G,使 a、G、b成等比数列,那么G叫做a与b的等比中项。
因此,
如果G是a与b的等比中项,那么
,即
小结作业
1.等比数列的基本特征可理解为:从 第2项起,每一项与它的前一项的比都 相等,并且可以用两种递推公式来描述.
2.等比数列的通项公式是由其定义推导出来的,确定一个等比数列需要两个独立条件.
3.等比数列与等差数列是两个并列概念,但二者有很大的差异,根据等比数列的定义和通项公式还可发掘出许多性质,具体内容待后探究.
作业:
P53习题2.4A组:1,2,3 .
