五年级下册数学一课一练-3.4长方体和正方体的体积计算 西师大版(word版,含答案)
文档属性
| 名称 | 五年级下册数学一课一练-3.4长方体和正方体的体积计算 西师大版(word版,含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 34.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 西师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-16 00:00:00 | ||
图片预览


文档简介
(
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
)
(
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
)
(
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
)
五年级下册数学一课一练-3.4长方体和正方体的体积计算
一、单选题
1.将6升水倒入一个长方体玻璃容器中(玻璃厚度不计),如果要计算容器中水面的高度,需要知道长方体玻璃容器的(???
).
A.?底面积?????????????????????????????????B.?侧面积?????????????????????????????????C.?表面积?????????????????????????????????D.?容积
2.最少用(???
)个完全一样的正方体就可以搭成一个较大的正方体。
A.?8?????????????????????????????????????????????B.?9?????????????????????????????????????????????C.?27
3.一个长方体容器,底面是正方形,盛水高1分米。放入6个质量一样的鸡蛋后,水面升高2厘米。要求一个鸡蛋的体积,只需要再知道(???
)。
A.?6个鸡蛋的表面积???????B.?长方体容器的表面积???????C.?长方体容器的高???????D.?长方体容器的底面周长
4.如图,一根长2
m的长方体木料沿虚线锯成两段后,表面积增加100
cm2
,
它的体积是(
????)。
A.?200
cm3????????????????????????????B.?10000
cm3????
????????????????????????????C.?2
dm3????????????????????????????D.?1
m3
二、判断题
5.正方体和长方体的体积都可以用底面积乘高来进行计算。(????
)
6.棱长是6cm的正方体,它的表面积与体积完全相等。(??
)
7.棱长为6cm的正方体的体积与表面积相等.
(
)
8.棱长6厘米的正方体的表面积和体积相等。(???
)
三、填空题
9.一个棱长是a厘米的正方体,它的所有棱长之和是________厘米,表面积是________平方厘米,体积是________立方厘米.
10.有一个长方体木块长9厘米,宽5厘米,高3厘米,如果把它切成1立方厘米的小方块,可以切出________块。
11.下面图形的体积是________
四、解答题
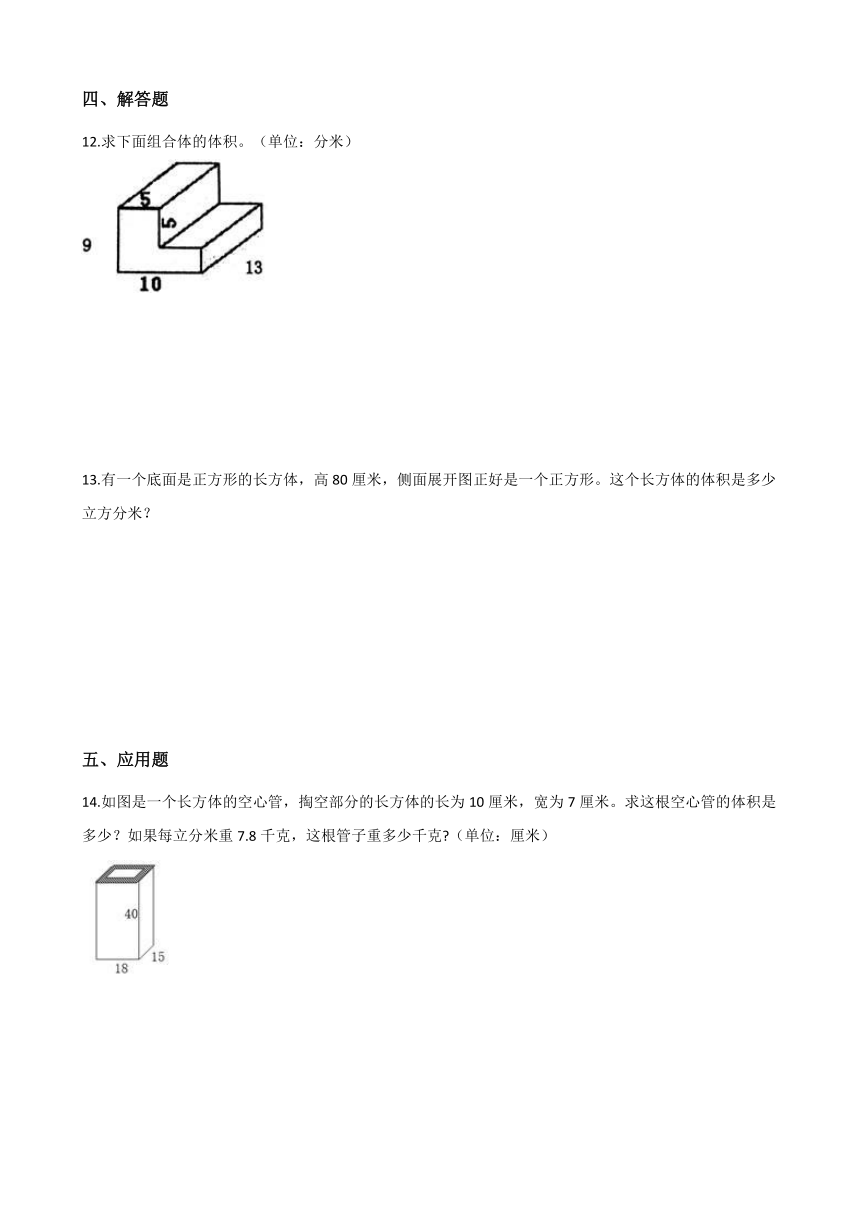
12.求下面组合体的体积。(单位:分米)
13.有一个底面是正方形的长方体,高80厘米,侧面展开图正好是一个正方形。这个长方体的体积是多少立方分米?
五、应用题
14.如图是一个长方体的空心管,掏空部分的长方体的长为10厘米,宽为7厘米。求这根空心管的体积是多少?如果每立分米重7.8千克,这根管子重多少千克?(单位:厘米)
参考答案
一、单选题
1.【答案】
A
【解析】【解答】解:将6升水倒入一个长方体玻璃容器中(玻璃厚度不计),如果要计算容器中水面的高度,需要知道长方体玻璃容器的底面积。
故答案为:A。
【分析】长方体的体积=长×宽×高=底面积×高,即要知道长方体的高,需要知道长方体的体积以及长方体的底面积。
2.【答案】
A
【解析】【解答】解:最少用8个完全一样的正方体就可以搭成一个较大的正方体。
故答案为:A。
【分析】用小正方体搭大正方体需要小正方体的个数为:2×2×2、3×3×3、……,据此进行解答即可。
3.【答案】
D
【解析】【解答】
一个长方体容器,底面是正方形,盛水高1分米。放入6个质量一样的鸡蛋后,水面升高2厘米。要求一个鸡蛋的体积,只需要再知道长方体容器的底面周长。
故答案为:D。
【分析】此题主要考查了不规则物体的体积计算,根据题意,鸡蛋放入水中后
,水面上升,上升部分的体积就是这些鸡蛋的体积,所以只需要再知道长方体容器的底面周长,这个长方体容器的底面是正方形,据此就可以求出正方形的边长,然后求出底面积,从而求出鸡蛋的体积,据此解答。
4.【答案】
B
【解析】【解答】解:2m=200cm,这根长方体木料的体积是:100÷2×200=1000cm3。
故答案为:B。
【分析】1m=100cm;这根长方体木料锯成两段后,这根木料就增加了两个底面的面积,长方体的体积=底面积×高,据此作答即可。
二、判断题
5.【答案】
正确
【解析】【解答】解:长方体和正方体的体积都可以用底面积乘高来进行计算。原题说法正确。
故答案为:正确。
【分析】长方体体积=长×宽×高,正方体体积=棱长×棱长×棱长,长×宽是长方体的底面积,棱长×棱长是正方体的底面积,所以长方体和正方体的体积都可以用底面积乘高来进行计算。
6.【答案】
错误
【解析】【解答】根据分析可知,表面积和体积是不同的两种量,不能比较大小,原题说法错误。
故答案为:错误。
【分析】已知正方体的棱长,求正方体的表面积,用公式:正方体的表面积=棱长×棱长×6,求正方体的体积,用公式:正方体的体积=棱长×棱长×棱长,表面积和体积的计算方法不同,计量单位也不同,表面积用面积单位,体积用体积单位,意义也不同,不能比较。
7.【答案】
错误
【解析】【解答】解:表面积:6×6×6=216(平方厘米)
体积:6×6×6=216(立方厘米)
因为表面积和体积不是同类量,无法进行比较.
故答案为:错误.
【分析】根据正方体的表面积公式:s=6a2
,
正方体的体积公式:v=a3
,
因为表面积和体积不是同类量,无法进行比较.由此解答.
8.【答案】
错误
【解析】【解答】解:正方体的表面积和体积的意义不同、计算方法不同、计量单位不同,所以无法比较大小。
故答案为:错误。
【分析】(1)意义不同,正方体的表面积是指组成正方体所有面的总面积,而正方体的体积是指正方体所占空间的大小;
(2)计算方法不同,正方体的表面积=棱长×棱长×6,而正方体体积=棱长×棱长×棱长;
(3)计量单位不同,表面积用面积单位,而体积用体积单位。
三、填空题
9.【答案】
12a;6a2;a3
【解析】【解答】a×12=12a;a×a×6=6a2;a×a×a=a3
故答案为:12a;6a2;a3
【分析】正方体有12条相等的棱,所以正方体棱长之和=棱长×12,正方体有6个完全一样的面,每一个面都是正方形,所以正方体表面积=棱长×棱长×6,正方体的体积=棱长×棱长×棱长。
10.【答案】
135
【解析】【解答】(9×5×3)÷(1×1×1)
=135÷1
=135(块)。
故答案为:135。
【分析】根据正方体的体积公式:V=a3,
长方体的体积公式:V=abh,分别求出正方体小方块的体积和长方体木块的体积,然后用长方体的体积除以正方体的体积即可。
11.【答案】
0.064立方米
【解析】【解答】0.4×0.4×0.4
=0.16×0.4
=0.064(立方米)
故答案为:0.064立方米.
【分析】已知正方体的棱长,要求表面积,用棱长×棱长×6=正方体的表面积,求体积,用公式:正方体的体积=棱长×棱长×棱长,据此解答.
四、解答题
12.【答案】
解:10-5=5(分米),9-5=4(分米),
5×4×13+9×5×13
=260+585
=845(立方分米)
【解析】【分析】分成左右两个长方形来计算体积,左边长方体长5分米、宽13分米、高9分米,右边长方体长(10-5)分米、宽13分米、高(9-5)分米,根据长方体体积公式计算总体积即可。
13.【答案】
解:80厘米=8分米
?
8÷4=2分米
?
2×2×8
=4×8
=32(立方分米)
答:这个长方体的体积是32立方分米。
【解析】【分析】根据条件“
有一个底面是正方形的长方体,高80厘米,侧面展开图正好是一个正方形
”可知,侧面展开图中,底面正方形的周长是80厘米,可以求出底面边长,也就是长方体的长与宽,然后用公式:长方体的体积=长×宽×高,据此列式解答。
五、应用题
14.【答案】
解:18×15×40-10×7×40=8000(立方厘米)
8000立方厘米=8立方分米
8×7.8=62.4(千克)
答:这根空心管的体积是8000立方厘米,这根管子重62.4千克。
【解析】【分析】这根空心管的体积=这个大长方体的体积-掏空部分长方体的体积,
长方体的体积=长×宽×高,这根管子重量=每立方分米的重量×这根空心管的体积;1立方分米=1000立方厘米。
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
)
(
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
)
(
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
)
五年级下册数学一课一练-3.4长方体和正方体的体积计算
一、单选题
1.将6升水倒入一个长方体玻璃容器中(玻璃厚度不计),如果要计算容器中水面的高度,需要知道长方体玻璃容器的(???
).
A.?底面积?????????????????????????????????B.?侧面积?????????????????????????????????C.?表面积?????????????????????????????????D.?容积
2.最少用(???
)个完全一样的正方体就可以搭成一个较大的正方体。
A.?8?????????????????????????????????????????????B.?9?????????????????????????????????????????????C.?27
3.一个长方体容器,底面是正方形,盛水高1分米。放入6个质量一样的鸡蛋后,水面升高2厘米。要求一个鸡蛋的体积,只需要再知道(???
)。
A.?6个鸡蛋的表面积???????B.?长方体容器的表面积???????C.?长方体容器的高???????D.?长方体容器的底面周长
4.如图,一根长2
m的长方体木料沿虚线锯成两段后,表面积增加100
cm2
,
它的体积是(
????)。
A.?200
cm3????????????????????????????B.?10000
cm3????
????????????????????????????C.?2
dm3????????????????????????????D.?1
m3
二、判断题
5.正方体和长方体的体积都可以用底面积乘高来进行计算。(????
)
6.棱长是6cm的正方体,它的表面积与体积完全相等。(??
)
7.棱长为6cm的正方体的体积与表面积相等.
(
)
8.棱长6厘米的正方体的表面积和体积相等。(???
)
三、填空题
9.一个棱长是a厘米的正方体,它的所有棱长之和是________厘米,表面积是________平方厘米,体积是________立方厘米.
10.有一个长方体木块长9厘米,宽5厘米,高3厘米,如果把它切成1立方厘米的小方块,可以切出________块。
11.下面图形的体积是________
四、解答题
12.求下面组合体的体积。(单位:分米)
13.有一个底面是正方形的长方体,高80厘米,侧面展开图正好是一个正方形。这个长方体的体积是多少立方分米?
五、应用题
14.如图是一个长方体的空心管,掏空部分的长方体的长为10厘米,宽为7厘米。求这根空心管的体积是多少?如果每立分米重7.8千克,这根管子重多少千克?(单位:厘米)
参考答案
一、单选题
1.【答案】
A
【解析】【解答】解:将6升水倒入一个长方体玻璃容器中(玻璃厚度不计),如果要计算容器中水面的高度,需要知道长方体玻璃容器的底面积。
故答案为:A。
【分析】长方体的体积=长×宽×高=底面积×高,即要知道长方体的高,需要知道长方体的体积以及长方体的底面积。
2.【答案】
A
【解析】【解答】解:最少用8个完全一样的正方体就可以搭成一个较大的正方体。
故答案为:A。
【分析】用小正方体搭大正方体需要小正方体的个数为:2×2×2、3×3×3、……,据此进行解答即可。
3.【答案】
D
【解析】【解答】
一个长方体容器,底面是正方形,盛水高1分米。放入6个质量一样的鸡蛋后,水面升高2厘米。要求一个鸡蛋的体积,只需要再知道长方体容器的底面周长。
故答案为:D。
【分析】此题主要考查了不规则物体的体积计算,根据题意,鸡蛋放入水中后
,水面上升,上升部分的体积就是这些鸡蛋的体积,所以只需要再知道长方体容器的底面周长,这个长方体容器的底面是正方形,据此就可以求出正方形的边长,然后求出底面积,从而求出鸡蛋的体积,据此解答。
4.【答案】
B
【解析】【解答】解:2m=200cm,这根长方体木料的体积是:100÷2×200=1000cm3。
故答案为:B。
【分析】1m=100cm;这根长方体木料锯成两段后,这根木料就增加了两个底面的面积,长方体的体积=底面积×高,据此作答即可。
二、判断题
5.【答案】
正确
【解析】【解答】解:长方体和正方体的体积都可以用底面积乘高来进行计算。原题说法正确。
故答案为:正确。
【分析】长方体体积=长×宽×高,正方体体积=棱长×棱长×棱长,长×宽是长方体的底面积,棱长×棱长是正方体的底面积,所以长方体和正方体的体积都可以用底面积乘高来进行计算。
6.【答案】
错误
【解析】【解答】根据分析可知,表面积和体积是不同的两种量,不能比较大小,原题说法错误。
故答案为:错误。
【分析】已知正方体的棱长,求正方体的表面积,用公式:正方体的表面积=棱长×棱长×6,求正方体的体积,用公式:正方体的体积=棱长×棱长×棱长,表面积和体积的计算方法不同,计量单位也不同,表面积用面积单位,体积用体积单位,意义也不同,不能比较。
7.【答案】
错误
【解析】【解答】解:表面积:6×6×6=216(平方厘米)
体积:6×6×6=216(立方厘米)
因为表面积和体积不是同类量,无法进行比较.
故答案为:错误.
【分析】根据正方体的表面积公式:s=6a2
,
正方体的体积公式:v=a3
,
因为表面积和体积不是同类量,无法进行比较.由此解答.
8.【答案】
错误
【解析】【解答】解:正方体的表面积和体积的意义不同、计算方法不同、计量单位不同,所以无法比较大小。
故答案为:错误。
【分析】(1)意义不同,正方体的表面积是指组成正方体所有面的总面积,而正方体的体积是指正方体所占空间的大小;
(2)计算方法不同,正方体的表面积=棱长×棱长×6,而正方体体积=棱长×棱长×棱长;
(3)计量单位不同,表面积用面积单位,而体积用体积单位。
三、填空题
9.【答案】
12a;6a2;a3
【解析】【解答】a×12=12a;a×a×6=6a2;a×a×a=a3
故答案为:12a;6a2;a3
【分析】正方体有12条相等的棱,所以正方体棱长之和=棱长×12,正方体有6个完全一样的面,每一个面都是正方形,所以正方体表面积=棱长×棱长×6,正方体的体积=棱长×棱长×棱长。
10.【答案】
135
【解析】【解答】(9×5×3)÷(1×1×1)
=135÷1
=135(块)。
故答案为:135。
【分析】根据正方体的体积公式:V=a3,
长方体的体积公式:V=abh,分别求出正方体小方块的体积和长方体木块的体积,然后用长方体的体积除以正方体的体积即可。
11.【答案】
0.064立方米
【解析】【解答】0.4×0.4×0.4
=0.16×0.4
=0.064(立方米)
故答案为:0.064立方米.
【分析】已知正方体的棱长,要求表面积,用棱长×棱长×6=正方体的表面积,求体积,用公式:正方体的体积=棱长×棱长×棱长,据此解答.
四、解答题
12.【答案】
解:10-5=5(分米),9-5=4(分米),
5×4×13+9×5×13
=260+585
=845(立方分米)
【解析】【分析】分成左右两个长方形来计算体积,左边长方体长5分米、宽13分米、高9分米,右边长方体长(10-5)分米、宽13分米、高(9-5)分米,根据长方体体积公式计算总体积即可。
13.【答案】
解:80厘米=8分米
?
8÷4=2分米
?
2×2×8
=4×8
=32(立方分米)
答:这个长方体的体积是32立方分米。
【解析】【分析】根据条件“
有一个底面是正方形的长方体,高80厘米,侧面展开图正好是一个正方形
”可知,侧面展开图中,底面正方形的周长是80厘米,可以求出底面边长,也就是长方体的长与宽,然后用公式:长方体的体积=长×宽×高,据此列式解答。
五、应用题
14.【答案】
解:18×15×40-10×7×40=8000(立方厘米)
8000立方厘米=8立方分米
8×7.8=62.4(千克)
答:这根空心管的体积是8000立方厘米,这根管子重62.4千克。
【解析】【分析】这根空心管的体积=这个大长方体的体积-掏空部分长方体的体积,
长方体的体积=长×宽×高,这根管子重量=每立方分米的重量×这根空心管的体积;1立方分米=1000立方厘米。
