四年级下册数学一课一练-4.1认识三角形 西师大版(word版,含答案)
文档属性
| 名称 | 四年级下册数学一课一练-4.1认识三角形 西师大版(word版,含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 48.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 西师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-16 15:13:28 | ||
图片预览


文档简介
(
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
)
(
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
)
(
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
)
四年级下册数学一课一练-4.1认识三角形
一、单选题
1.下面关于角的叙述不正确的是(???
)。
A.?角的两边是射线??????????????????????????????????????????????????B.?角的大小是可以度量的。
C.?三角形内的角可能大于180度。??????????????????????????D.?角可以看作是射线绕其端点旋转而成。
2.三角形三个内角中,至少有(??
)
A.?一个钝角和一个锐角????????????????????????B.?两个锐角????????????????????????C.?一个锐角一个直角
3.如果一个三角形的两条边分别长5cm和8cm,另一条边可能是(??
)cm。
A.?3?????????????????????????????????????????????B.?7?????????????????????????????????????????????C.?14
4.下列说法中,正确的是(??
)。
A.?直角三角形的两条直角边互相垂直??????????????????????B.?三角形三个内角中可以有一个钝角,一个直角
C.?两个锐角的和一定比直角大????????????????????????????????D.?周角的大小是平角的4倍
二、判断题
5.直角三角形只有一条高。(
)
6.任意三角形的内角和都是180°。(???
)
7.三角形中最大的角不小于60度。(
)
8.三条边分别是5厘米、5厘米、10厘米的三角形是一个等腰三角形.(??
)
三、填空题
9.一个直角三角形,已知一个角是45°,另一个角是________。
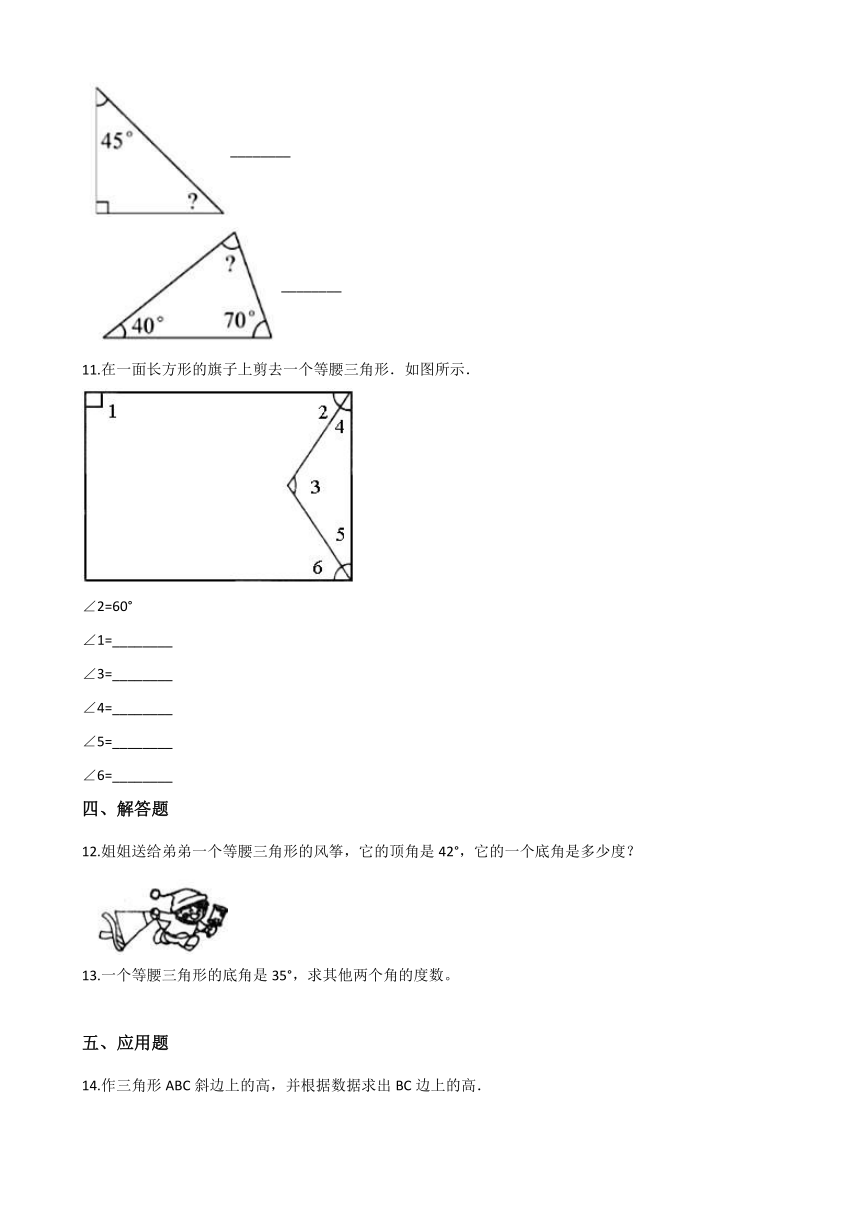
10.算出下面各个未知角的度数。
________
________
________
________
11.在一面长方形的旗子上剪去一个等腰三角形.如图所示.
∠2=60°
∠1=________
∠3=________
∠4=________
∠5=________
∠6=________
四、解答题
12.姐姐送给弟弟一个等腰三角形的风筝,它的顶角是42°,它的一个底角是多少度?
13.一个等腰三角形的底角是35°,求其他两个角的度数。
五、应用题
14.作三角形ABC斜边上的高,并根据数据求出BC边上的高.
参考答案
一、单选题
1.【答案】
C
【解析】【解答】A:角的两边是射线,正确;
B:角的大小是可以度量的,正确;
C:三角形的内角和是180度,不可能大于180度,所以说法错误;
D:角可以看作是射线绕其端点旋转而成,正确。
故答案为:C。
【分析】根据角的概念和三角形内角和的度数来判断即可。
2.【答案】
B
【解析】【解答】解:三角形三个内角中,至少有两个锐角。
故答案为:B。
【分析】三角形内角和是180°,如果最大角是钝角或直角,那么另外两个角一定是锐角;如果最大角是锐角,那么三个角都是锐角。
3.【答案】
B
【解析】【解答】8-5=3(厘米),8+5=13(厘米)
另一条边应大于3厘米,小于13厘米。
故答案为:B。
【分析】在一个三角形中,任意两边之和大于第三边,任意两边之差小于第三边。
?
4.【答案】
A
【解析】【解答】选项A,直角三角形的两条直角边互相垂直,原题说法正确;
选项B,三角形三个内角中最多只有1个钝角或1个直角,原题说法错误;
选项C,在钝角三角形中,两个锐角的和小于直角,在直角三角形中,两个锐角的和等于直角,原题说法错误;
选项D,周角的大小是平角的2倍,原题说法错误。
故答案为:A。
【分析】在直角三角形中,直角三角形的两条直角边互相垂直;三角形的内角和是180°,三角形三个内角中最多只有1个钝角或1个直角;在钝角三角形中,两个锐角的和小于直角,在直角三角形中,两个锐角的和等于直角;周角=360°,平角=180°,一个周角=2个平角,据此判断。
二、判断题
5.【答案】
错误
【解析】【解答】直角三角形有3条高,其中两条高就是两条直角边,原题说法错误.
故答案为:错误.
【分析】任何一个三角形都有3条高,据此判断.
6.【答案】
正确
【解析】【解答】解:任意三角形的内角和都是180°,说法正确。
故答案为:正确。
【分析】三角形的内角和是180°,本题据此判断即可。
7.【答案】
正确
【解析】【解答】假设三角形的最大内角小于60°,那么三角形的内角和就小于180°,与三角形内角和为180°相矛盾。
因此三角形中最大的内角不能小于60°;
故答案为:正确。
【分析】根据三角形的内角和等于180°,然后运用假设法,即可得出结论。
8.【答案】
错误
【解析】【解答】解:因为5+5=10,所以三条边分别是5厘米、5厘米、10厘米不能围成三角形,所以本题说法错误。
故答案为:错误。
【分析】三角形任意两边之和大于第三边,任意两边之差小于第三边。题中两边之和等于第三边,所以不能围成三角形。
三、填空题
9.【答案】
45°
【解析】【解答】三角形的内角和为
?,
故答案为:45°.
【分析】根据三角形的内角和是180°,直角三角形中有一个直角,用三角形的内角和-直角-已知锐角的度数=要求的锐角度数,据此解答.
10.【答案】
;;;
【解析】【解答】180°-60°-60°
=120°-60°
=60°
180°-30°-125°
=150°-125°
=25°
90°-45°=45°
180°-40°-70°
=140°-70°
=70°
【分析】三角形内角和是180°,用180°减去知道的两个角的度数,就可以求出第三个角的度数.
11.【答案】
90;120;30;30;60
【解析】【解答】∠1=90°、
∠4=90°-∠2=90°-60°=30°
∠5=∠4=30°
∠6=90°-∠5=90°-30°=60°
∠3=180°-∠4-∠5=180°-30°-30°=120°
故答案为:90、120、30、30、60
【分析】根据长方形的四个角都是直角,等腰三角形两个底角相等,内角和是180度进行解答.
四、解答题
12.【答案】
解:(180°-42°)÷2
=138°÷2
=69°
答:它的一个底角是69度。
【解析】【分析】等腰三角形两个底角度数相等,用三角形内角和减去顶角的度数即可求出两个底角的度数,再除以2即可求出一个底角的度数。
13.【答案】
解:180°-35°×2°=110°
答:其他两个角分别是35°和110°
【解析】【分析】等腰三角形的两个底角相等,三角形内角和-底角度数×2=顶角度数。
五、应用题
14.【答案】
解:6×8÷2×2÷10
=48÷2×2÷10
=48÷10
=4.8(个长度单位);
答:BC边上的高是
4.8.
故答案为:4.8.
【解析】【分析】三角形ABC是直角三角形,AB和AC是两条直角边,已知底是6,高是8,根据三角形的面积公式求出它的面积,又已知斜边长是10,即可求出斜边上的高.此题主要根据三角形的高的意义和三角形的面积计算公式解决问题.
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
)
(
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
)
(
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
)
四年级下册数学一课一练-4.1认识三角形
一、单选题
1.下面关于角的叙述不正确的是(???
)。
A.?角的两边是射线??????????????????????????????????????????????????B.?角的大小是可以度量的。
C.?三角形内的角可能大于180度。??????????????????????????D.?角可以看作是射线绕其端点旋转而成。
2.三角形三个内角中,至少有(??
)
A.?一个钝角和一个锐角????????????????????????B.?两个锐角????????????????????????C.?一个锐角一个直角
3.如果一个三角形的两条边分别长5cm和8cm,另一条边可能是(??
)cm。
A.?3?????????????????????????????????????????????B.?7?????????????????????????????????????????????C.?14
4.下列说法中,正确的是(??
)。
A.?直角三角形的两条直角边互相垂直??????????????????????B.?三角形三个内角中可以有一个钝角,一个直角
C.?两个锐角的和一定比直角大????????????????????????????????D.?周角的大小是平角的4倍
二、判断题
5.直角三角形只有一条高。(
)
6.任意三角形的内角和都是180°。(???
)
7.三角形中最大的角不小于60度。(
)
8.三条边分别是5厘米、5厘米、10厘米的三角形是一个等腰三角形.(??
)
三、填空题
9.一个直角三角形,已知一个角是45°,另一个角是________。
10.算出下面各个未知角的度数。
________
________
________
________
11.在一面长方形的旗子上剪去一个等腰三角形.如图所示.
∠2=60°
∠1=________
∠3=________
∠4=________
∠5=________
∠6=________
四、解答题
12.姐姐送给弟弟一个等腰三角形的风筝,它的顶角是42°,它的一个底角是多少度?
13.一个等腰三角形的底角是35°,求其他两个角的度数。
五、应用题
14.作三角形ABC斜边上的高,并根据数据求出BC边上的高.
参考答案
一、单选题
1.【答案】
C
【解析】【解答】A:角的两边是射线,正确;
B:角的大小是可以度量的,正确;
C:三角形的内角和是180度,不可能大于180度,所以说法错误;
D:角可以看作是射线绕其端点旋转而成,正确。
故答案为:C。
【分析】根据角的概念和三角形内角和的度数来判断即可。
2.【答案】
B
【解析】【解答】解:三角形三个内角中,至少有两个锐角。
故答案为:B。
【分析】三角形内角和是180°,如果最大角是钝角或直角,那么另外两个角一定是锐角;如果最大角是锐角,那么三个角都是锐角。
3.【答案】
B
【解析】【解答】8-5=3(厘米),8+5=13(厘米)
另一条边应大于3厘米,小于13厘米。
故答案为:B。
【分析】在一个三角形中,任意两边之和大于第三边,任意两边之差小于第三边。
?
4.【答案】
A
【解析】【解答】选项A,直角三角形的两条直角边互相垂直,原题说法正确;
选项B,三角形三个内角中最多只有1个钝角或1个直角,原题说法错误;
选项C,在钝角三角形中,两个锐角的和小于直角,在直角三角形中,两个锐角的和等于直角,原题说法错误;
选项D,周角的大小是平角的2倍,原题说法错误。
故答案为:A。
【分析】在直角三角形中,直角三角形的两条直角边互相垂直;三角形的内角和是180°,三角形三个内角中最多只有1个钝角或1个直角;在钝角三角形中,两个锐角的和小于直角,在直角三角形中,两个锐角的和等于直角;周角=360°,平角=180°,一个周角=2个平角,据此判断。
二、判断题
5.【答案】
错误
【解析】【解答】直角三角形有3条高,其中两条高就是两条直角边,原题说法错误.
故答案为:错误.
【分析】任何一个三角形都有3条高,据此判断.
6.【答案】
正确
【解析】【解答】解:任意三角形的内角和都是180°,说法正确。
故答案为:正确。
【分析】三角形的内角和是180°,本题据此判断即可。
7.【答案】
正确
【解析】【解答】假设三角形的最大内角小于60°,那么三角形的内角和就小于180°,与三角形内角和为180°相矛盾。
因此三角形中最大的内角不能小于60°;
故答案为:正确。
【分析】根据三角形的内角和等于180°,然后运用假设法,即可得出结论。
8.【答案】
错误
【解析】【解答】解:因为5+5=10,所以三条边分别是5厘米、5厘米、10厘米不能围成三角形,所以本题说法错误。
故答案为:错误。
【分析】三角形任意两边之和大于第三边,任意两边之差小于第三边。题中两边之和等于第三边,所以不能围成三角形。
三、填空题
9.【答案】
45°
【解析】【解答】三角形的内角和为
?,
故答案为:45°.
【分析】根据三角形的内角和是180°,直角三角形中有一个直角,用三角形的内角和-直角-已知锐角的度数=要求的锐角度数,据此解答.
10.【答案】
;;;
【解析】【解答】180°-60°-60°
=120°-60°
=60°
180°-30°-125°
=150°-125°
=25°
90°-45°=45°
180°-40°-70°
=140°-70°
=70°
【分析】三角形内角和是180°,用180°减去知道的两个角的度数,就可以求出第三个角的度数.
11.【答案】
90;120;30;30;60
【解析】【解答】∠1=90°、
∠4=90°-∠2=90°-60°=30°
∠5=∠4=30°
∠6=90°-∠5=90°-30°=60°
∠3=180°-∠4-∠5=180°-30°-30°=120°
故答案为:90、120、30、30、60
【分析】根据长方形的四个角都是直角,等腰三角形两个底角相等,内角和是180度进行解答.
四、解答题
12.【答案】
解:(180°-42°)÷2
=138°÷2
=69°
答:它的一个底角是69度。
【解析】【分析】等腰三角形两个底角度数相等,用三角形内角和减去顶角的度数即可求出两个底角的度数,再除以2即可求出一个底角的度数。
13.【答案】
解:180°-35°×2°=110°
答:其他两个角分别是35°和110°
【解析】【分析】等腰三角形的两个底角相等,三角形内角和-底角度数×2=顶角度数。
五、应用题
14.【答案】
解:6×8÷2×2÷10
=48÷2×2÷10
=48÷10
=4.8(个长度单位);
答:BC边上的高是
4.8.
故答案为:4.8.
【解析】【分析】三角形ABC是直角三角形,AB和AC是两条直角边,已知底是6,高是8,根据三角形的面积公式求出它的面积,又已知斜边长是10,即可求出斜边上的高.此题主要根据三角形的高的意义和三角形的面积计算公式解决问题.
