苏科版数学九年级上册2.1.1 圆 课件(20张PPT)
文档属性
| 名称 | 苏科版数学九年级上册2.1.1 圆 课件(20张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-16 00:00:00 | ||
图片预览




文档简介
(共20张PPT)
2.1 圆(1)
九年级(上册)
初中数学
套圈游戏
生活·活动
2.1
圆(1)
只有一个小立柱,若全班同学沿着红线站成一横排,请问游戏对所有同学公平吗?谈谈你的想法.
小立柱
生活·活动
2.1
圆(1)
位置:
1.一段(两端已打结)的棉线.
2.一段(两端已打结)的皮筋.
你能和你的同桌合作,利用它们,以及手中的笔,
在练习纸上分别作出圆吗?试一试.
为大家提供了两件物品:
数学·思考
2.1
圆(1)
大小:
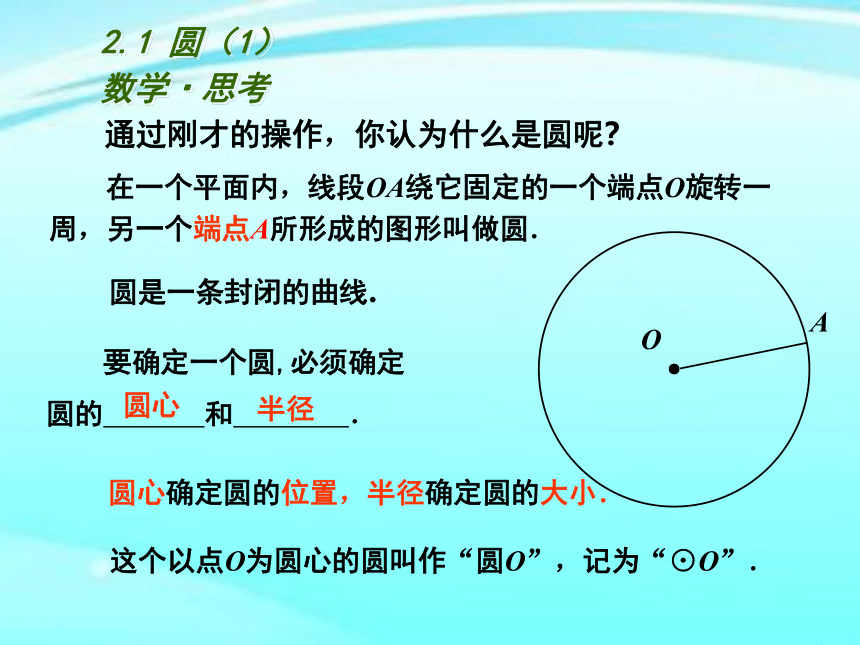
要确定一个圆,必须确定
圆的
和
.
在一个平面内,线段OA绕它固定的一个端点O旋转一周,另一个端点A所形成的图形叫做圆.
圆心确定圆的位置,半径确定圆的大小.
这个以点O为圆心的圆叫作“圆O”,记为“⊙O”.
圆心
半径
圆是一条封闭的曲线.
通过刚才的操作,你认为什么是圆呢?
●
O
A
数学·思考
2.1
圆(1)
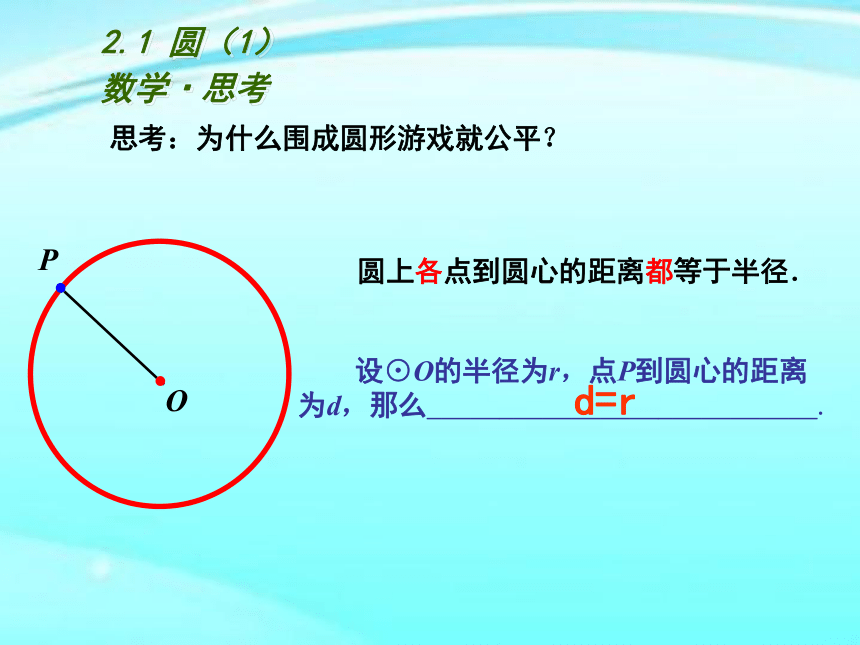
圆上各点到圆心的距离都等于半径.
设⊙O的半径为r,点P到圆心的距离
为d,那么___________________________.
P
思考:为什么围成圆形游戏就公平?
O
数学·思考
2.1
圆(1)
d=r
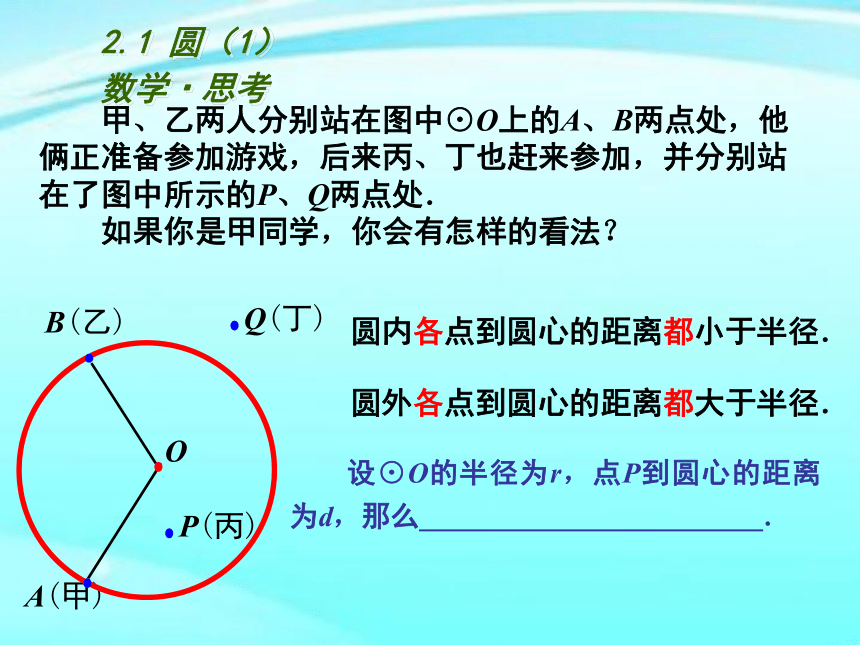
圆内各点到圆心的距离都小于半径.
圆外各点到圆心的距离都大于半径.
设⊙O的半径为r,点P到圆心的距离为d,那么
.
O
A(甲)
P(丙)
Q(丁)
甲、乙两人分别站在图中⊙O上的A、B两点处,他俩正准备参加游戏,后来丙、丁也赶来参加,并分别站在了图中所示的P、Q两点处.
如果你是甲同学,你会有怎样的看法?
B(乙)
数学·思考
2.1
圆(1)
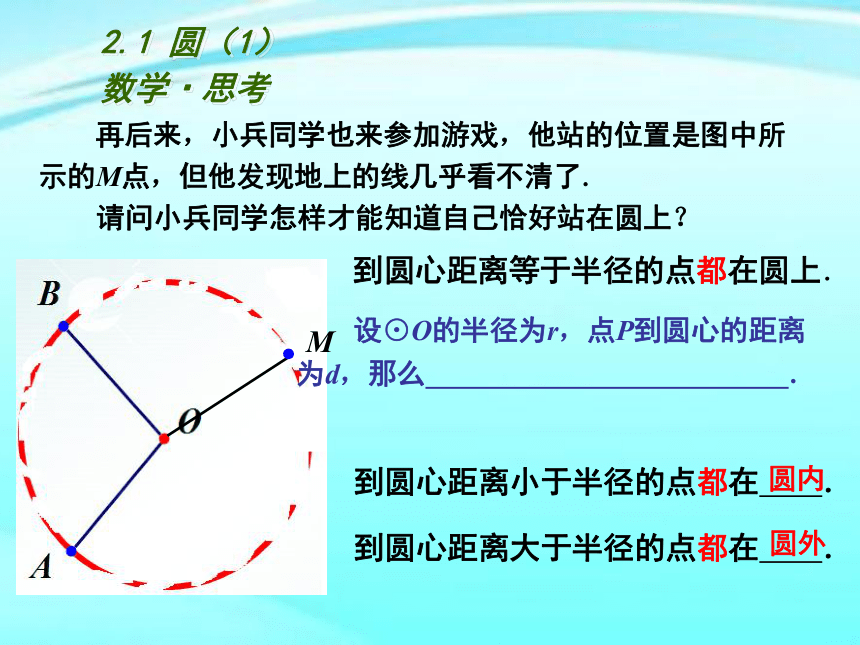
到圆心距离等于半径的点都在圆上.
再后来,小兵同学也来参加游戏,他站的位置是图中所示的M点,但他发现地上的线几乎看不清了.
请问小兵同学怎样才能知道自己恰好站在圆上?
M
设⊙O的半径为r,点P到圆心的距离
为d,那么
.
到圆心距离小于半径的点都在
.
到圆心距离大于半径的点都在
.
圆内
圆外
数学·思考
2.1
圆(1)
回到游戏
圆是
点的集合.
平面内到定点的距离等于定长的
圆的内部是
点的集合.
圆的外部是
点的集合.
平面内到圆心的距离小于半径的
平面内到圆心的距离大于半径的
数学·思考
2.1
圆(1)
例1 已知⊙O的半径为4cm,如果点P到圆心O的距离为4.5cm,那么点P与⊙O有怎样的位置关系?如果点P到圆心O的距离为4cm、3cm呢?
如何判断点与圆的位置关系?
只需要比较点到圆心的距离d与半径r的大小关系.
解:
设⊙O的半径为rcm,点P到圆心O的距离为dcm.
由题意得,r=4cm.
当d=4.5cm时,
∵
d>r,∴点P在⊙O外.
当d=4cm时,
∵
d=r,∴点P在⊙O上.
当d=3cm时,
∵
d<r,∴点P在⊙O内.
知识运用
2.1
圆(1)
如图,已知点A,请作出到点A的距离等于2cm的点的集合.
(1)这个圆的外部是满足什么条件的点的集合?
(2)请用阴影表示出到点A的距离小于或等于2cm的点的集合.
A
知识运用
2.1
圆(1)
d>2的点
如图,已知点A、B,且AB=4cm.
(1)画出下列图形:
到点A的距离等于2cm的点的集合;
到点B的距离等于3cm的点的集合.
P
Q
B
A
2.1
圆(1)
(2)在所画图中,到点A的距离等于2cm,且到点B的距离等于3cm的点有几个?请在图中将它们表示出来.
(3)在所画图中,到点A的距离小于或等于2cm,且到点B的距离大于或等于3cm的点的集合是怎样的图形?把它表示出来.
⊙A
⊙B
两个
⊙A与⊙B的交点
⊙A及内部
⊙B及内部
1、⊙O的半径10cm,A、B、C三点到圆心的距离分别是8、10、12cm,则点A、B、C与⊙O的位置关系是:点A在
;点B在
;点C在
。
⊙O内
⊙O上
⊙O外
2、⊙O的半径6cm,
当OP=6cm时,点P在
;
当OP
时,点P在圆内;
当OP
时,点P在圆外。
⊙O上
<6cm
>6cm
3、正方形ABCD的边长是2cm,以A为圆心,
2cm为半径作⊙A,则点B在⊙A
;点C在⊙A
,点D在⊙A
.
上
外
上
练一练
1、已知⊙M的半径r=2,点P是平面的一个点。
(1)当PM=2时,点P在⊙M
;
(2)当PM=5时,点P在⊙M
;
(3)当PM=1时,点P在⊙M
。
上
外
内
自我测试
2、已知⊙O的面积是25π,判断点P与⊙O
的位置关系。
(1)当PO=5.5时,点P在⊙O
;
(2)当PO=4时,点P在⊙O
;
(3)当PO=
时,点P在圆上。
外
内
5
3、如图,在Rt△ABC中,∠C是直角,AC=4,BC=3,E、F分别是AB、AC的中点,以B为圆心,BC为半径画圆,试判断A、C、E、F与圆B的位置关系。
A
B
C
E
F
应用拓展
1、已知矩形ABCD的对角线AC、BD相交于点O,点A、B、C、D是否在以点O为圆心的同一个圆上?为什么?
∵四边形ABCD
是矩形
∴OA=OB=OC=OD
∴点A、B、C、D在以点O为圆心,OA为半径的同一个圆上
已知:如图,BD、CE是△ABC的高,M为BC的中点.试说明点
B、C、D、E在以点M为圆心的同一圆上.
解题的依据:
要说明几点在同一个圆上,即说明这几个点到定点(圆心)的距离等于定长(半径).
到定点的距离等于定长的点在同一个圆上.
2.1
圆(1)
∴点B、C、D、E在以点M为圆心,
为半径的圆上.
解:
连接MD、ME.
∵BD、CE是△ABC的高,
同理,
∴MB=ME=MD=MC,
又∵
已知:如图,BD、CE是△ABC的高,M为BC的中点.
试说明点
B、C、D、E在以点M为圆心的同一圆上.
2.1
圆(1)
∴∠BEC=∠BDC=90°.
在Rt△BEC中,M为BC的中点,
通过今天的学习,你能谈谈你对圆有什么新的认识吗?
课本P40第1、2、3题.
课后作业
小结与思考
2.1
圆(1)
红日、满月、飞轮、硬币……圆的形象处处可见.
平面图形中,圆象征着完美、和谐.
2.1
圆(1)
2.1 圆(1)
九年级(上册)
初中数学
套圈游戏
生活·活动
2.1
圆(1)
只有一个小立柱,若全班同学沿着红线站成一横排,请问游戏对所有同学公平吗?谈谈你的想法.
小立柱
生活·活动
2.1
圆(1)
位置:
1.一段(两端已打结)的棉线.
2.一段(两端已打结)的皮筋.
你能和你的同桌合作,利用它们,以及手中的笔,
在练习纸上分别作出圆吗?试一试.
为大家提供了两件物品:
数学·思考
2.1
圆(1)
大小:
要确定一个圆,必须确定
圆的
和
.
在一个平面内,线段OA绕它固定的一个端点O旋转一周,另一个端点A所形成的图形叫做圆.
圆心确定圆的位置,半径确定圆的大小.
这个以点O为圆心的圆叫作“圆O”,记为“⊙O”.
圆心
半径
圆是一条封闭的曲线.
通过刚才的操作,你认为什么是圆呢?
●
O
A
数学·思考
2.1
圆(1)
圆上各点到圆心的距离都等于半径.
设⊙O的半径为r,点P到圆心的距离
为d,那么___________________________.
P
思考:为什么围成圆形游戏就公平?
O
数学·思考
2.1
圆(1)
d=r
圆内各点到圆心的距离都小于半径.
圆外各点到圆心的距离都大于半径.
设⊙O的半径为r,点P到圆心的距离为d,那么
.
O
A(甲)
P(丙)
Q(丁)
甲、乙两人分别站在图中⊙O上的A、B两点处,他俩正准备参加游戏,后来丙、丁也赶来参加,并分别站在了图中所示的P、Q两点处.
如果你是甲同学,你会有怎样的看法?
B(乙)
数学·思考
2.1
圆(1)
到圆心距离等于半径的点都在圆上.
再后来,小兵同学也来参加游戏,他站的位置是图中所示的M点,但他发现地上的线几乎看不清了.
请问小兵同学怎样才能知道自己恰好站在圆上?
M
设⊙O的半径为r,点P到圆心的距离
为d,那么
.
到圆心距离小于半径的点都在
.
到圆心距离大于半径的点都在
.
圆内
圆外
数学·思考
2.1
圆(1)
回到游戏
圆是
点的集合.
平面内到定点的距离等于定长的
圆的内部是
点的集合.
圆的外部是
点的集合.
平面内到圆心的距离小于半径的
平面内到圆心的距离大于半径的
数学·思考
2.1
圆(1)
例1 已知⊙O的半径为4cm,如果点P到圆心O的距离为4.5cm,那么点P与⊙O有怎样的位置关系?如果点P到圆心O的距离为4cm、3cm呢?
如何判断点与圆的位置关系?
只需要比较点到圆心的距离d与半径r的大小关系.
解:
设⊙O的半径为rcm,点P到圆心O的距离为dcm.
由题意得,r=4cm.
当d=4.5cm时,
∵
d>r,∴点P在⊙O外.
当d=4cm时,
∵
d=r,∴点P在⊙O上.
当d=3cm时,
∵
d<r,∴点P在⊙O内.
知识运用
2.1
圆(1)
如图,已知点A,请作出到点A的距离等于2cm的点的集合.
(1)这个圆的外部是满足什么条件的点的集合?
(2)请用阴影表示出到点A的距离小于或等于2cm的点的集合.
A
知识运用
2.1
圆(1)
d>2的点
如图,已知点A、B,且AB=4cm.
(1)画出下列图形:
到点A的距离等于2cm的点的集合;
到点B的距离等于3cm的点的集合.
P
Q
B
A
2.1
圆(1)
(2)在所画图中,到点A的距离等于2cm,且到点B的距离等于3cm的点有几个?请在图中将它们表示出来.
(3)在所画图中,到点A的距离小于或等于2cm,且到点B的距离大于或等于3cm的点的集合是怎样的图形?把它表示出来.
⊙A
⊙B
两个
⊙A与⊙B的交点
⊙A及内部
⊙B及内部
1、⊙O的半径10cm,A、B、C三点到圆心的距离分别是8、10、12cm,则点A、B、C与⊙O的位置关系是:点A在
;点B在
;点C在
。
⊙O内
⊙O上
⊙O外
2、⊙O的半径6cm,
当OP=6cm时,点P在
;
当OP
时,点P在圆内;
当OP
时,点P在圆外。
⊙O上
<6cm
>6cm
3、正方形ABCD的边长是2cm,以A为圆心,
2cm为半径作⊙A,则点B在⊙A
;点C在⊙A
,点D在⊙A
.
上
外
上
练一练
1、已知⊙M的半径r=2,点P是平面的一个点。
(1)当PM=2时,点P在⊙M
;
(2)当PM=5时,点P在⊙M
;
(3)当PM=1时,点P在⊙M
。
上
外
内
自我测试
2、已知⊙O的面积是25π,判断点P与⊙O
的位置关系。
(1)当PO=5.5时,点P在⊙O
;
(2)当PO=4时,点P在⊙O
;
(3)当PO=
时,点P在圆上。
外
内
5
3、如图,在Rt△ABC中,∠C是直角,AC=4,BC=3,E、F分别是AB、AC的中点,以B为圆心,BC为半径画圆,试判断A、C、E、F与圆B的位置关系。
A
B
C
E
F
应用拓展
1、已知矩形ABCD的对角线AC、BD相交于点O,点A、B、C、D是否在以点O为圆心的同一个圆上?为什么?
∵四边形ABCD
是矩形
∴OA=OB=OC=OD
∴点A、B、C、D在以点O为圆心,OA为半径的同一个圆上
已知:如图,BD、CE是△ABC的高,M为BC的中点.试说明点
B、C、D、E在以点M为圆心的同一圆上.
解题的依据:
要说明几点在同一个圆上,即说明这几个点到定点(圆心)的距离等于定长(半径).
到定点的距离等于定长的点在同一个圆上.
2.1
圆(1)
∴点B、C、D、E在以点M为圆心,
为半径的圆上.
解:
连接MD、ME.
∵BD、CE是△ABC的高,
同理,
∴MB=ME=MD=MC,
又∵
已知:如图,BD、CE是△ABC的高,M为BC的中点.
试说明点
B、C、D、E在以点M为圆心的同一圆上.
2.1
圆(1)
∴∠BEC=∠BDC=90°.
在Rt△BEC中,M为BC的中点,
通过今天的学习,你能谈谈你对圆有什么新的认识吗?
课本P40第1、2、3题.
课后作业
小结与思考
2.1
圆(1)
红日、满月、飞轮、硬币……圆的形象处处可见.
平面图形中,圆象征着完美、和谐.
2.1
圆(1)
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
