甘肃省会宁县2020-2021学年高二下学期期末考试数学试题(文科) Word版含解析
文档属性
| 名称 | 甘肃省会宁县2020-2021学年高二下学期期末考试数学试题(文科) Word版含解析 |  | |
| 格式 | docx | ||
| 文件大小 | 718.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-17 00:01:54 | ||
图片预览




文档简介
会宁县2020-2021学年第二学期期末考试高二数学(文科)试卷
一、选择题(每小题5分,共60分)
1.已知集合false,false,则false( )
A.false B.false C.false D.false
2.设false,i为虚数单位,且false是实数,则false的值为( )
A.1 B.false C.0 D.false
3.在平面直角坐标系中,抛物线false经过伸缩变换false后得到的曲线方程是( )
A.false B.false C.false D.false
4.小明用流程图把早上上班前需要做的事情做了如图方案,则所用时间最少
A.23分 B.24分钟 C.26分钟 D.31分钟
5.对于样本相关系数,下列说法错误的是( )
A.可以用来判断成对样本数据相关的正负性 B.可以是正的,也可以是负的
C.样本相关系数越大,成对样本数据的线性相关程度也越高 D.取值范围是false
6.设false的三边长分别为false,false,false,若false的面积为false,内切圆半径为false,则false,类比这个结论可知:若四面体false的四个面的面积分别为false,false,false,false,内切球半径为false,四面体false的体积为false,则false( )
A.false B.false
C.false D.false
7.两个变量y与x的回归模型中,分别选择了4个不同模型,它们的相关指数R2如下,其中拟合效果最好的模型是( )
A.模型1的相关指数R2为0.98 B.模型2的相关指数R2为0.80
C.模型3的相关指数R2为0.50 D.模型4的相关指数R2为0.25
8. 执行如图所示的程序框图,输出S的值为
A.-false B.false C.-false D.false
9.用反证法证明命题“已知false,如果false可被3整除,那么false中至少有一个能被3整除”时,假设的内容应为( )
A.false都不能被3整除 B.false都能被3整除
C.false不都能被3整除 D.false不能被3整除
10.已知false,false,是不同的直线,false,false是不重合的平面,则下列说法正确的是( )
A.若false,则false平行于平面false内的任意一条直线 B.若false,false,则false
C.若false,false,false,则false D.若false,false,则false
11.如图所示,n个连续自然数按规律排列如下:
根据规律,从2014到2016的箭头方向依次为( )
A.→↑ B.↑→ C.↓→ D.→↓
12.若false,对任意的false,都有false,且false.设false表示整数false的个位数,则false为( )
A.false B.false C.false D.false
二、填空题(每小题5分,共20分)
13.已知复数false满足false为虚数单位false,则false的最大值是__________.
14.某超市为回馈顾客,制作了6元,8元,10元三种面值的代金券各两张用于抽奖活动.现顾客甲?乙?丙三人每人从中抽取两张,已知每个人抽取的两张券上的面值都不一样.甲看了乙的券后说:“我与乙的两张券上相同的面值不是8元”,乙看了丙的券后说:“我与丙的两张券上相同的面值不是6元”,丙说:“我的两张券上的面值之和不是18元”,若三人所说为真,则乙抽的两张券的面值之和是___________元.
15.已知实数x,y满足方程false,则false的最大值为________.
16.若函数false的图象与直线y=a有交点,则实数a的取值范围是 _______.
三、解答题
17.(12分)已知z是复数,且false和false都是实数,其中i是虚数单位.
(1)求复数z和false;
(2)若复数false在复平面内对应的点位于第三象限,求实数m的取值范围.
18.(12分)(1)设false,证明:false;
(2)已知false,证明:false.
19.(12分)某研究机构对某校高二文科学生的记忆力false和判断力false进行统计分析,得下表数据.
false
6
8
10
12
false
2
3
5
6
(1)请根据上表提供的数据,用最小二乘法求出false关于false的线性回归方程;
(2)试根据(2)中求出的线性回归方程,预测记忆力为14的学生的判断力.
(参考公式:其中false)
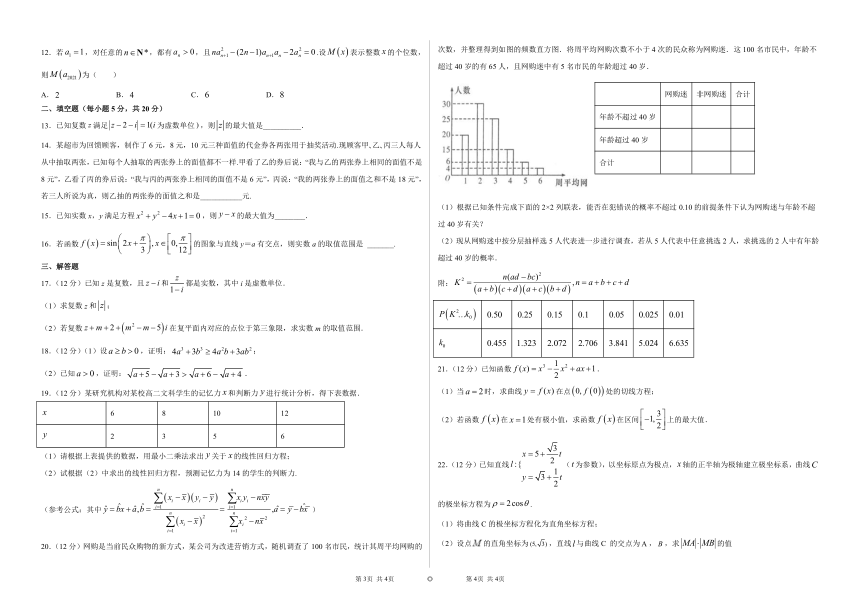
20.(12分)网购是当前民众购物的新方式,某公司为改进营销方式,随机调查了100名市民,统计其周平均网购的次数,并整理得到如图的频数直方图.将周平均网购次数不小于4次的民众称为网购迷.这100名市民中,年龄不超过40岁的有65人,且网购迷中有5名市民的年龄超过40岁.
网购迷
非网购迷
合计
年龄不超过40岁
年龄超过40岁
合计
(1)根据已知条件完成下面的2×2列联表,能否在犯错误的概率不超过0.10的前提条件下认为网购迷与年龄不超过40岁有关?
(2)现从网购迷中按分层抽样选5人代表进一步进行调查,若从5人代表中任意挑选2人,求挑选的2人中有年龄超过40岁的概率.
附:false
false
false
false
false
false
false
false
false
false
false
false
false
false
false
false
false
21.(12分)已知函数false.
(1)当false时,求曲线false在点false处的切线方程;
(2)若函数false在false处有极小值,求函数false在区间false上的最大值.
22.(12分)已知直线false(false为参数),以坐标原点为极点,false轴的正半轴为极轴建立极坐标系,曲线false的极坐标方程为false.
(1)将曲线C的极坐标方程化为直角坐标方程;
(2)设点的直角坐标为false,直线false与曲线C 的交点为false,false,求false的值
高二数学参考答案
1.【答案】B
【分析】
根据交集的概念和运算直接求解出false的结果.
【详解】
解:∵false,false,
∴false.
故选:B.
2.【答案】B
【详解】
false,所以false的虚部为false.故选B.
3.A
【分析】
先根据导数的几何意义求出曲线false在false处的切线方程,再求出积分的上下限,然后利用定积分表示出图形面积,最后利用定积分进行求解即可.
【详解】
解:false的导数为false,
可得false在点false处的切线的斜率为false,
切线的方程为false,即false,
可得切线与该曲线及false轴围成的封闭图形的面积为
false
故选:A
4.B
【分析】
利用正态分布密度函数的对称性将求false 转化为false,进而可得结果.
【详解】
如图,正态分布的密度函数示意图所示,
函数图象关于直线false对称,所以false,
则false.
故选:B.
【点睛】
关键点点睛:应用正态分布密度函数图象的对称性是解决本题的关键.
5.B
【分析】
求导后求得函数的单调性,利用单调性求得函数的最小值.
【详解】
因为false,所以false在false上单调递减,在false上单调递增,所以false.
故答案为:B.
6.D
【分析】
根据符号法则将不等式转化为两个不等式组,结合图象即可解出.
【详解】
原不等式等价于false或false,结合false的图象可得,
false或false,解得false或false或false.
故选:D.
7.D
【分析】
由题意分析:每个贫困户只能选择一个扶贫项目,每个项目至少有一户选择,基本事件总数false,而甲乙两户选择同一个扶贫项目包含的基本事件个数false,利用古典概型的概率公式求概率即可.
【详解】
由题意分析:
若每个贫困户只能选择一个扶贫项目,每个项目至少有一户选择,
基本事件总数false,
甲乙两户选择同一个扶贫项目包含的基本事件个数false,
则甲乙两户选择同一个扶贫项目的概率false.
故选:D.
8.【答案】A
【分析】
由已知结合等差数列和的性质即可求解.
【详解】
因数列false?false都为等差数列,且false,
故设false,false,
因此false,false,
由等差中项得,false.
故选:A.
9.B
【分析】
根据方差公式求出方差,再判断即可.
【详解】
由分布列可得false,
故false.
故选:B
【点睛】
关键点点睛:解决本题的关键是熟练掌握期望和方差的公式.
10.A
【分析】
设事件A为“30人中抽出一名女同学”,事件false为“30人中抽出一名高三同学”,分别求得false,false,代入条件概率公式,即可得答案.
【详解】
设事件A为“30人中抽出一名女同学”,事件false为“30人中抽出一名高三同学”,
则false,false,
所以false,
故选:A.
11.C
【分析】
根据二项分布的特点,列举出(xk,yk)的所有情况,可得答案.
【详解】
根据二项分布的特点,知(xk,yk)分别为(0,20),(1,19),(2,18),…,(20,0),共21个,故选:C.
12.D
【分析】
作出函数的图象,根据对称性可以知道false,结合图象可得到false,进而得到false,由对数函数的性质进一步判定false,
从而根据在false时false,根据其单调性和已经得到的false的范围得到结论.
【详解】
作出false的大致图象如下:
由图可知false,
令false,得false,
所以false,则false.
因为false,所以false,
又当false时,false单调递减,
所以false,
故选:D.
【点睛】
本题考查利用函数的图象和性质求范围问题,涉及分段函数的图象,指数型函数图象和性质,对数函数的性质,属综合题,关键是数形结合思想的应用,函数的图象的对称性和单调性的应用.
13.false
【分析】
求出展开式的通项,然后令false的指数为2,求出false的值,在代入通项中进行化简,即可求得结果.
【详解】
false的展开式的通项公式为:false,
令false,解得false,
所以false的系数是false.
故答案为:false.
14.false
【分析】
由偶函数易得false关于false对称求参数b,根据图象过点求参数c,写出解析式即可.
【详解】
∵false是偶函数,有false,
∴false关于false对称,即false,故false,又图像经过点false,
∴false,可得false.
故false.
故答案为:false
15.0.42
【分析】
根据所给得分规则求出70分时立定跳远距离,再求出105分时的立定跳远距离,即可求解.
【详解】
该生成绩为70分时,其立定跳远距离为false米,
该生成绩为105分时,其立定跳远距离为false米,
所以增加了false米,
故答案为:0.42
16.false
【分析】
利用导函数可知在false上false,有false单调递减,即可求区间内最小值.
【详解】
在false上,有false,
知:false在false上单调递减,在false和false上单调递增,故最大值在极大值点或端点值处取得,极大值为false,最大的端点值为false,
明显地,false,所以,false在false上的最大值是false
故答案为:false
17.【答案】(1)曲线false普通方程为false曲线false的直角坐标方程为false(2)false
【分析】
(1)将曲线false的参数方程中的t消掉得到曲线false的普通方程,利用ρcosθ=x,ρsinθ=y,能求出C2的直角坐标方程.
(2)将false代入false,得false,利用直线参数的几何意义结合韦达定理,能求出false.
【详解】
(1)曲线false的参数方程为false(false为参数),两式相加消去t可得普通方程为false;又由ρcosθ=x,ρsinθ=y,
曲线false的极坐标方程为false转化为直角坐标方程为false
(2)把曲线false的参数方程为false(false为参数),代入false得false,
设false,false是false对应的参数,则false,false
所以false false
18.【答案】(1)false;(2)false
【分析】
(1)利用正弦定理将边化角,再根据两角和的正弦公式、诱导公式计算可得;
(2)由false,false,得false,再利用余弦定理求出false,即可求出false的周长.
【详解】
解:(1)因为false,所以false,
所以false,即false,因为false,所以false,
所以false,所以false
(2)false,false,
false,
false,false
false,
false的周长为:false.
19.(1)false;(2)分布列见解析,false.
【分析】
(1)利用至少有一个正确的概率为false直接计算即可;
(2)先根据题意判断false的取值,并计算各取值对应的概率,即得到分布列,再计算false即得小明闯关成功的概率.
【详解】
解:(1)设事件false为小明回答正确第一个问题,事件false为小明回答正确第二个问题,则false为小明回答错误第一个问题,false为小明回答错误第二个问题,false,false.
所以小明回答第一,第二个问题,至少有一个正确的概率为:
false;
(2)设事件false为小明回答正确第三个问题,
由题知,小明在闯关赛中,回答题目正确的个数false的取值为0,1,2,3,
所以false,
falsefalse
false,
falsefalse,
false.
故false的分布列为:
false
0
1
2
3
false
false
false
false
false
所以小明闯关成功的概率为false.
【点睛】
思路点睛:
求离散型随机变量的分布列及期望的一般步骤:
(1)根据题中条件确定随机变量的可能取值;
(2)求出随机变量所有可能取值对应的概率,即可得出分布列.
20.(1)false,false;(2)单调递增区间为false和false,单调递减区间为false和false.
【分析】
(1)求出false,然后利用false求解即可;
(2)false,然后求解即可.
【详解】
(1)false,
又false和false为false的两根,
false,
故有false,
解方程组得false,false.
(2)false,false,
false,
令false得false,false,false,
当false时,false;
当false时,false,
false的单调递增区间为false和false,单调递减区间为false和false.
21.(1)列联表答案见解析,没有false的把握认为学生是否肥胖和经常饮用碳酸饮料有关;(2)分布列答案见解析,数学期望:false.
【详解】
(1)
经常饮用
不经常饮用
合计
肥胖
8
10
18
不肥胖
7
15
22
合计
15
25
40
由调查数据可知,false的观测值false
没有false的把握认为学生是否肥胖和经常饮用碳酸饮料有关.
(2)被选中的男生人数false的取值为2,3,4,5
则false,false,
false,false
分布列为
false
2
3
4
5
false
false
false
false
false
期望false.
22.(1)false;(2)false在false上的极值点的个数为1.
【分析】
(1)等价于false对任意false恒成立,设false,求出false即得解;
(2)设false,求出函数false在false上的极值点的个数即得解.
【详解】
(1)false
所以false,
设false,
所以false,
因为false,所以false,
所以false,所以函数false在false单调递减,
所以false,所以false.
(2)若false, false,
设false,
所以false,
所以false在false上单调递增,在false单调递减,
false
设false,对称轴为false,false时,false,
所以false
当false时,false,当false时,false,
所以在false,函数false没有零点,false,使得false,
即false,使得false,且false是唯一的,
所以false在false上的极值点的个数为1.
【点睛】
关键点睛:解答本题的关键有二,其一,是二次求导,得到false在false上单调递增,在false单调递减,其二,是分析得到函数false在false上的极值点的个数.
一、选择题(每小题5分,共60分)
1.已知集合false,false,则false( )
A.false B.false C.false D.false
2.设false,i为虚数单位,且false是实数,则false的值为( )
A.1 B.false C.0 D.false
3.在平面直角坐标系中,抛物线false经过伸缩变换false后得到的曲线方程是( )
A.false B.false C.false D.false
4.小明用流程图把早上上班前需要做的事情做了如图方案,则所用时间最少
A.23分 B.24分钟 C.26分钟 D.31分钟
5.对于样本相关系数,下列说法错误的是( )
A.可以用来判断成对样本数据相关的正负性 B.可以是正的,也可以是负的
C.样本相关系数越大,成对样本数据的线性相关程度也越高 D.取值范围是false
6.设false的三边长分别为false,false,false,若false的面积为false,内切圆半径为false,则false,类比这个结论可知:若四面体false的四个面的面积分别为false,false,false,false,内切球半径为false,四面体false的体积为false,则false( )
A.false B.false
C.false D.false
7.两个变量y与x的回归模型中,分别选择了4个不同模型,它们的相关指数R2如下,其中拟合效果最好的模型是( )
A.模型1的相关指数R2为0.98 B.模型2的相关指数R2为0.80
C.模型3的相关指数R2为0.50 D.模型4的相关指数R2为0.25
8. 执行如图所示的程序框图,输出S的值为
A.-false B.false C.-false D.false
9.用反证法证明命题“已知false,如果false可被3整除,那么false中至少有一个能被3整除”时,假设的内容应为( )
A.false都不能被3整除 B.false都能被3整除
C.false不都能被3整除 D.false不能被3整除
10.已知false,false,是不同的直线,false,false是不重合的平面,则下列说法正确的是( )
A.若false,则false平行于平面false内的任意一条直线 B.若false,false,则false
C.若false,false,false,则false D.若false,false,则false
11.如图所示,n个连续自然数按规律排列如下:
根据规律,从2014到2016的箭头方向依次为( )
A.→↑ B.↑→ C.↓→ D.→↓
12.若false,对任意的false,都有false,且false.设false表示整数false的个位数,则false为( )
A.false B.false C.false D.false
二、填空题(每小题5分,共20分)
13.已知复数false满足false为虚数单位false,则false的最大值是__________.
14.某超市为回馈顾客,制作了6元,8元,10元三种面值的代金券各两张用于抽奖活动.现顾客甲?乙?丙三人每人从中抽取两张,已知每个人抽取的两张券上的面值都不一样.甲看了乙的券后说:“我与乙的两张券上相同的面值不是8元”,乙看了丙的券后说:“我与丙的两张券上相同的面值不是6元”,丙说:“我的两张券上的面值之和不是18元”,若三人所说为真,则乙抽的两张券的面值之和是___________元.
15.已知实数x,y满足方程false,则false的最大值为________.
16.若函数false的图象与直线y=a有交点,则实数a的取值范围是 _______.
三、解答题
17.(12分)已知z是复数,且false和false都是实数,其中i是虚数单位.
(1)求复数z和false;
(2)若复数false在复平面内对应的点位于第三象限,求实数m的取值范围.
18.(12分)(1)设false,证明:false;
(2)已知false,证明:false.
19.(12分)某研究机构对某校高二文科学生的记忆力false和判断力false进行统计分析,得下表数据.
false
6
8
10
12
false
2
3
5
6
(1)请根据上表提供的数据,用最小二乘法求出false关于false的线性回归方程;
(2)试根据(2)中求出的线性回归方程,预测记忆力为14的学生的判断力.
(参考公式:其中false)
20.(12分)网购是当前民众购物的新方式,某公司为改进营销方式,随机调查了100名市民,统计其周平均网购的次数,并整理得到如图的频数直方图.将周平均网购次数不小于4次的民众称为网购迷.这100名市民中,年龄不超过40岁的有65人,且网购迷中有5名市民的年龄超过40岁.
网购迷
非网购迷
合计
年龄不超过40岁
年龄超过40岁
合计
(1)根据已知条件完成下面的2×2列联表,能否在犯错误的概率不超过0.10的前提条件下认为网购迷与年龄不超过40岁有关?
(2)现从网购迷中按分层抽样选5人代表进一步进行调查,若从5人代表中任意挑选2人,求挑选的2人中有年龄超过40岁的概率.
附:false
false
false
false
false
false
false
false
false
false
false
false
false
false
false
false
false
21.(12分)已知函数false.
(1)当false时,求曲线false在点false处的切线方程;
(2)若函数false在false处有极小值,求函数false在区间false上的最大值.
22.(12分)已知直线false(false为参数),以坐标原点为极点,false轴的正半轴为极轴建立极坐标系,曲线false的极坐标方程为false.
(1)将曲线C的极坐标方程化为直角坐标方程;
(2)设点的直角坐标为false,直线false与曲线C 的交点为false,false,求false的值
高二数学参考答案
1.【答案】B
【分析】
根据交集的概念和运算直接求解出false的结果.
【详解】
解:∵false,false,
∴false.
故选:B.
2.【答案】B
【详解】
false,所以false的虚部为false.故选B.
3.A
【分析】
先根据导数的几何意义求出曲线false在false处的切线方程,再求出积分的上下限,然后利用定积分表示出图形面积,最后利用定积分进行求解即可.
【详解】
解:false的导数为false,
可得false在点false处的切线的斜率为false,
切线的方程为false,即false,
可得切线与该曲线及false轴围成的封闭图形的面积为
false
故选:A
4.B
【分析】
利用正态分布密度函数的对称性将求false 转化为false,进而可得结果.
【详解】
如图,正态分布的密度函数示意图所示,
函数图象关于直线false对称,所以false,
则false.
故选:B.
【点睛】
关键点点睛:应用正态分布密度函数图象的对称性是解决本题的关键.
5.B
【分析】
求导后求得函数的单调性,利用单调性求得函数的最小值.
【详解】
因为false,所以false在false上单调递减,在false上单调递增,所以false.
故答案为:B.
6.D
【分析】
根据符号法则将不等式转化为两个不等式组,结合图象即可解出.
【详解】
原不等式等价于false或false,结合false的图象可得,
false或false,解得false或false或false.
故选:D.
7.D
【分析】
由题意分析:每个贫困户只能选择一个扶贫项目,每个项目至少有一户选择,基本事件总数false,而甲乙两户选择同一个扶贫项目包含的基本事件个数false,利用古典概型的概率公式求概率即可.
【详解】
由题意分析:
若每个贫困户只能选择一个扶贫项目,每个项目至少有一户选择,
基本事件总数false,
甲乙两户选择同一个扶贫项目包含的基本事件个数false,
则甲乙两户选择同一个扶贫项目的概率false.
故选:D.
8.【答案】A
【分析】
由已知结合等差数列和的性质即可求解.
【详解】
因数列false?false都为等差数列,且false,
故设false,false,
因此false,false,
由等差中项得,false.
故选:A.
9.B
【分析】
根据方差公式求出方差,再判断即可.
【详解】
由分布列可得false,
故false.
故选:B
【点睛】
关键点点睛:解决本题的关键是熟练掌握期望和方差的公式.
10.A
【分析】
设事件A为“30人中抽出一名女同学”,事件false为“30人中抽出一名高三同学”,分别求得false,false,代入条件概率公式,即可得答案.
【详解】
设事件A为“30人中抽出一名女同学”,事件false为“30人中抽出一名高三同学”,
则false,false,
所以false,
故选:A.
11.C
【分析】
根据二项分布的特点,列举出(xk,yk)的所有情况,可得答案.
【详解】
根据二项分布的特点,知(xk,yk)分别为(0,20),(1,19),(2,18),…,(20,0),共21个,故选:C.
12.D
【分析】
作出函数的图象,根据对称性可以知道false,结合图象可得到false,进而得到false,由对数函数的性质进一步判定false,
从而根据在false时false,根据其单调性和已经得到的false的范围得到结论.
【详解】
作出false的大致图象如下:
由图可知false,
令false,得false,
所以false,则false.
因为false,所以false,
又当false时,false单调递减,
所以false,
故选:D.
【点睛】
本题考查利用函数的图象和性质求范围问题,涉及分段函数的图象,指数型函数图象和性质,对数函数的性质,属综合题,关键是数形结合思想的应用,函数的图象的对称性和单调性的应用.
13.false
【分析】
求出展开式的通项,然后令false的指数为2,求出false的值,在代入通项中进行化简,即可求得结果.
【详解】
false的展开式的通项公式为:false,
令false,解得false,
所以false的系数是false.
故答案为:false.
14.false
【分析】
由偶函数易得false关于false对称求参数b,根据图象过点求参数c,写出解析式即可.
【详解】
∵false是偶函数,有false,
∴false关于false对称,即false,故false,又图像经过点false,
∴false,可得false.
故false.
故答案为:false
15.0.42
【分析】
根据所给得分规则求出70分时立定跳远距离,再求出105分时的立定跳远距离,即可求解.
【详解】
该生成绩为70分时,其立定跳远距离为false米,
该生成绩为105分时,其立定跳远距离为false米,
所以增加了false米,
故答案为:0.42
16.false
【分析】
利用导函数可知在false上false,有false单调递减,即可求区间内最小值.
【详解】
在false上,有false,
知:false在false上单调递减,在false和false上单调递增,故最大值在极大值点或端点值处取得,极大值为false,最大的端点值为false,
明显地,false,所以,false在false上的最大值是false
故答案为:false
17.【答案】(1)曲线false普通方程为false曲线false的直角坐标方程为false(2)false
【分析】
(1)将曲线false的参数方程中的t消掉得到曲线false的普通方程,利用ρcosθ=x,ρsinθ=y,能求出C2的直角坐标方程.
(2)将false代入false,得false,利用直线参数的几何意义结合韦达定理,能求出false.
【详解】
(1)曲线false的参数方程为false(false为参数),两式相加消去t可得普通方程为false;又由ρcosθ=x,ρsinθ=y,
曲线false的极坐标方程为false转化为直角坐标方程为false
(2)把曲线false的参数方程为false(false为参数),代入false得false,
设false,false是false对应的参数,则false,false
所以false false
18.【答案】(1)false;(2)false
【分析】
(1)利用正弦定理将边化角,再根据两角和的正弦公式、诱导公式计算可得;
(2)由false,false,得false,再利用余弦定理求出false,即可求出false的周长.
【详解】
解:(1)因为false,所以false,
所以false,即false,因为false,所以false,
所以false,所以false
(2)false,false,
false,
false,false
false,
false的周长为:false.
19.(1)false;(2)分布列见解析,false.
【分析】
(1)利用至少有一个正确的概率为false直接计算即可;
(2)先根据题意判断false的取值,并计算各取值对应的概率,即得到分布列,再计算false即得小明闯关成功的概率.
【详解】
解:(1)设事件false为小明回答正确第一个问题,事件false为小明回答正确第二个问题,则false为小明回答错误第一个问题,false为小明回答错误第二个问题,false,false.
所以小明回答第一,第二个问题,至少有一个正确的概率为:
false;
(2)设事件false为小明回答正确第三个问题,
由题知,小明在闯关赛中,回答题目正确的个数false的取值为0,1,2,3,
所以false,
falsefalse
false,
falsefalse,
false.
故false的分布列为:
false
0
1
2
3
false
false
false
false
false
所以小明闯关成功的概率为false.
【点睛】
思路点睛:
求离散型随机变量的分布列及期望的一般步骤:
(1)根据题中条件确定随机变量的可能取值;
(2)求出随机变量所有可能取值对应的概率,即可得出分布列.
20.(1)false,false;(2)单调递增区间为false和false,单调递减区间为false和false.
【分析】
(1)求出false,然后利用false求解即可;
(2)false,然后求解即可.
【详解】
(1)false,
又false和false为false的两根,
false,
故有false,
解方程组得false,false.
(2)false,false,
false,
令false得false,false,false,
当false时,false;
当false时,false,
false的单调递增区间为false和false,单调递减区间为false和false.
21.(1)列联表答案见解析,没有false的把握认为学生是否肥胖和经常饮用碳酸饮料有关;(2)分布列答案见解析,数学期望:false.
【详解】
(1)
经常饮用
不经常饮用
合计
肥胖
8
10
18
不肥胖
7
15
22
合计
15
25
40
由调查数据可知,false的观测值false
没有false的把握认为学生是否肥胖和经常饮用碳酸饮料有关.
(2)被选中的男生人数false的取值为2,3,4,5
则false,false,
false,false
分布列为
false
2
3
4
5
false
false
false
false
false
期望false.
22.(1)false;(2)false在false上的极值点的个数为1.
【分析】
(1)等价于false对任意false恒成立,设false,求出false即得解;
(2)设false,求出函数false在false上的极值点的个数即得解.
【详解】
(1)false
所以false,
设false,
所以false,
因为false,所以false,
所以false,所以函数false在false单调递减,
所以false,所以false.
(2)若false, false,
设false,
所以false,
所以false在false上单调递增,在false单调递减,
false
设false,对称轴为false,false时,false,
所以false
当false时,false,当false时,false,
所以在false,函数false没有零点,false,使得false,
即false,使得false,且false是唯一的,
所以false在false上的极值点的个数为1.
【点睛】
关键点睛:解答本题的关键有二,其一,是二次求导,得到false在false上单调递增,在false单调递减,其二,是分析得到函数false在false上的极值点的个数.
同课章节目录
